2. 中国石油长庆油田分公司, 陕西 西安 710000;
3. 中国石化西南油气分公司博士后科研工作站, 四川 成都 610041;
4. 中国石化西南油气分公司勘探开发研究院, 四川 成都 610041
2. ChangQing Oil Field Filiale, Petrochina, Xi′an, Shaanxi 710000, China;
3. Post-Doctoral Scientific Research Station, Southwest Oil & Gas Branch Company, SINOPEC, Chengdu, Sichuan 610041, China;
4. Exploration & Production Research Institute, Southwest Oil & Gas Branch Company, SINOPEC, Chengdu, Sichuan 610041, China
目前,预测油田产量的方法主要有递减曲线法、增长曲线法和水驱曲线法等[1-7],但是上述方法都是针对有很长井史的老井而言,且为单变量,对于勘探开发初期油井产量预测明显不合时宜。如何建立一个勘探时期有效的试油层产量预测模型,指导油田勘探试油迫在眉睫。
邢明海等[8]研究了产量预测的多元线性回归模型,综合考虑各种地质因素及人为因素对油产量的影响,并与神经网络模型进行了对比分析,但仅考虑了各影响因素与产量的线性关系。刘秀婷等[9]应用多元线性混合回归模型建立新老区产量综合预测的模型。常规的多变量预测模型[10-15]不足之处在于,仅考虑产量与各影响因素的线性关系,而大部分影响因素存在着非线性关系,因此用线性代替非线性务必会存在较大的偏差,且波动较大,适用性差。本文通过对与有产量相关的多个变量进行综合回归分析,选出影响油井产量的重要因素并建立多元非线性回归产量预测模型,应用于实际勘探时期的产量预测。
1 非线性产量预测模型 1.1 一元非线性回归模型油田开发是一个极其复杂的多参数变量非线性动力学系统,因此,试油层产量与各影响因素也应该为非线性关系。令试油层产量为因变量Y,各个与产量有关的参数(如:孔隙度、渗透率、厚度等)为自变量x,且自变量一共有p个。首先,根据因变量Y与p个自变量的关系,分别建立Y对各
一般先建立如下7种常用的初等函数,然后对建立的7种初等函数进行比较检验(检验参数常见有:标准误差,相关系数,残差序列随机性检验统计量等),最后每个自变量得到一个与因变量相关的最佳一元回归模型
| $ {Y_i} = {f_i}\left( {{x_i}} \right) $ | (1) |
常用的初等函数有:
(1) 线性函数
(2) 指数函数
(3) 分式指数函数
(4) 幂函数
(5) 对数函数
(6) 双曲线函数
(7) 高阶函数
多元线性回归是一种数理统计方法,其基本思想是用多个自变量的最优组合共同来预测或估计因变量。
令试油层产量为因变量Y,并将前面建立的最佳一元回归模型
设随机误差为
| $ Y = {\beta _0} + {\beta _1}{X_1} + {\beta _2}{X_2} + {\beta _3}{X_3}.........{\beta _p}{X_p} + \xi $ | (2) |
对于试油层产量预测问题,如果获得n组观测数据(
| $ {Y_i} \!=\! {\beta _0} \!+\! {\beta _1}{X_{i1}} \!+\! {\beta _2}{X_{i2}} \!+\! {\beta _3}{X_{i3}} \cdots \!+\! {\beta _p}{X_{ip}} \!+\! {\xi _i} $ | (3) |
其矩阵形式为
| $ {\boldsymbol{Y}} = {\boldsymbol{X}} {\boldsymbol{β}} + {\boldsymbol{ξ}} $ | (4) |
式中:
采用最小二乘估计法拟合,最小二乘估计法是使估计值
| $ Q = \sum\limits_1^{\rm{n}} {{\boldsymbol{e}}_i^2} = {\boldsymbol{e}}{\rm{'}}{\boldsymbol {e}} =\sum(y - {x^\beta }){\rm{'(}}y{\rm{ - }}{x^\beta }) $ | (5) |
式中:
Q-二乘法值;
要使Q达到最小,根据极值原理,需满足式(6)和式(7);联合式(6)和式(7)共p+1方程构成正规方程组,解此正规方程组可得到参数的最小二乘估计值。
| $\dfrac{{\partial Q}}{{\partial {\beta _i}}} = 0\begin{array}{*{20}{c}} {} & {} \end{array}(i = 0, 1, 2, \cdots, p) $ | (6) |
| $ \left\{ \begin{array}{l} \sum\limits_{i = 1}^n {2{e_i}( - 1) = } \\{\kern 12pt} \!-\! 1\sum\limits_{i = 1}^n {\left[{{y_i} \!-\! \left( {{{\hat \beta }_0} \!+\! {{\hat \beta }_1}{x_{i1}} \!+\! \cdots + {{\hat \beta }_0}{x_{ip}}} \right)} \right] = 0} \\ \sum\limits_{i = 1}^n {2{e_i}( - {x_{i1}}) = } \\{\kern 12pt} \!-\! 2\sum\limits_{i = 1}^n {\left[{{y_i}{x_{i1}} \!-\! \left( {{{\hat \beta }_0} \!+\! {{\hat \beta }_1}{x_{i1}} \!+\! \cdots \!+\! {{\hat \beta }_0}{x_{ip}}} \right)} \right] = 0} \\ {\kern 80pt}\vdots \\ \sum\limits_{i = 1}^n {2{e_i}( - {x_{ip}}) = } \\{\kern 12pt} \!-\! 2\sum\limits_{i = 1}^n {\left[{{y_i}{x_{ip}} \!-\! \left( {{{\hat \beta }_0} \!+\! {{\hat \beta }_1}{x_{i1}} \!+\! \cdots \!+\! {{\hat \beta }_0}{x_{ip}}} \right)} \right] = 0} \end{array} \right. $ | (7) |
式(7)可用正规方程组矩阵表示为
| $ \left( {\begin{array}{*{20}{c}} {\sum\limits_{i = 1}^n {{e_i}} }\\ {\sum\limits_{i = 1}^n {{X_{i1}}{e_i}} }\\ \vdots \\ {\sum\limits_{i = 1}^n {{X_{ip}}{e_i}} } \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1 & 1 & \cdots & 1\\ {{X_{11}}} & {{X_{21}}} & \cdots & {{X_{n1}}}\\ \vdots & \vdots & \vdots & \vdots \\ {{X_{1p}}} & {{X_{2p}}} & \cdots & {{X_{np}}} \end{array}} \right) = {\boldsymbol{X}}'{\boldsymbol{e}} = 0 $ | (8) |
由样本回归模型
| $ {\boldsymbol{X}}'{\boldsymbol{Y}} = {\boldsymbol{X}}'\hat{{\boldsymbol{X}}}{\boldsymbol{β}} + {\boldsymbol{X}}'{\boldsymbol{β}} $ | (9) |
极值条件得正规方程组
| $ {\boldsymbol{X}}'{\boldsymbol{Y}} = {\boldsymbol{X}}'{{\boldsymbol{X}}}\hat{{\boldsymbol{β}}} $ | (10) |
当
| $ \hat {{\boldsymbol{β}}} = {\left( {{\boldsymbol{X}}'{\boldsymbol{X}}} \right)^{ - 1}}{\boldsymbol{X}}'{\boldsymbol{Y}} $ | (11) |
根据回归系数的最小二乘估计式(11),便可以得到检验回归效果的5项参数:残差平方和q、回归平方和
| $ q = \sum\limits_{i = 1}^n {({y_i} - {{\hat y}_i}} {)^2} $ | (12) |
| $ \mu = \sum\limits_{i = 1}^{\rm{n}} {({{\hat y}_i}} - \overline {{y}} {)^2} $ | (13) |
| $ F = \dfrac{{\mu /p}}{{q/(n - p - 1)}} $ | (14) |
| $ r = \sqrt {\mu /(\mu + q)} $ | (15) |
| $ {t_j} = \dfrac{{{{\hat \beta }_j}}}{{\sqrt {{C_{ij}}\left[{q/(n-p-1} \right]} }} $ | (16) |
| $ {C_{ij}} = {\left( {X'X} \right)^{ - 1}} {\kern 6pt}i, j = 0, 1, 2, \cdots, p $ | (17) |
式中:
F统计量表示了多元线性回归方程的显著性,该值服从F分布。它们必须满足一定的显著性检验要求。相关系数r表示回归方程对原始数据拟合程度的好坏,越接近1说明回归效果越好。在回归效果较差的情况下,根据
| $ Y = {\beta _0} + {\beta _1}{f_1}({x_1}) + {\beta _2}{f_2}({x_2}) + {\beta _3}{f_3}({x_3})+\\[6pt]{\kern 42pt}\cdots+{\beta _p}{f_p}({x_p}) + \xi $ | (18) |
根据本文的多元非线性回归方法,结合勘探开发初期已有的井的资料及信息,对即将要开发的井进行产量预测,降低其试油经济风险。利用多元非线性回归预测措施产量的步骤如下:
(1) 确定准备参数
根据勘探区块已开发井的资料及信息,综合静态地质资料(钻井、测井、录井、岩芯、地震等)和动态资料(试井测试、试油、措施等),确定与产量密切相关的静、动态参数。
(2) 建立最佳一元回归模型
以开发井的产量为因变量,步骤(1)中确定的各静、动态参数作为自变量,建立其产量—各参数的最佳一元回归模型。若某些参数与产量建立的一元回归模型相关性较差,则直接删除该参数。
(3) 构建回归模型
利用已开发井的资料数据作为回归样本,根据多元非线性回归方法,结合已建立的产量与各参数的最佳一元回归方程,再利用多元线性回归原理,最终构建一个以产量为因变量,各参数为自变量的多元非线性回归模型。
(4) 验证回归模型
为了验证建立的多元非线性回归模型的准确性,将回归样本的数据回代入已经建立的多元非线性产量预测模型中,计算预测产量与原产量的相对误差,是否满足其预测精度,若不满足则需返回步骤(3),剔除线性回归时相关性差的参数。
(5) 预测
将所选取的预测井的各参数代入已经建立的回归模型中,计算预测的产量。
2 实例预测某勘探区块,属低孔、低渗的差储层,非均质性强,大大地增加了试油层产量预测的难度。统计该区块已开发井的静、动态资料,研究其各井产量与之对应的静、态参数的相关性,最后选取了4个静态参数(厚度、气测全烃增量、孔隙度和含油饱和度)和2个动态参数(试井渗透率和10 h压力恢复速率)作为产量预测模型的自变量x,其勘探区块已开发井优选参数数据见表 1(h-厚度,m;
| 表1 勘探区块试油层参数汇总及模型预测结果 Table 1 oil-testing formation parameter and predicted results in model of exploration blocks |
根据产量预测的步骤,首先建立6个静、动态参数与试油层产量的一元回归模型为
| $ \left\{ \begin{array}{l} {X_1} = h\\ {X_2} = {\rm{e}}^{ \left(0.0444\Delta M \right)}\\ {X_3} = \ln \left(0.0022\phi + 1.0599\right)\\ {X_4} = {S_{\rm{o}}}\\ {X_5} = \lg (K)\\ {X_6} = \ln \left( {0.0036{v_{\rm{p}}} + 1.1308} \right) \end{array} \right. $ | (19) |
根据式(19),一元回归模型的因变量变为新的自变量(表 2),日产量作为因变量Y,构建多元线性回归模型(式(20)),其该回归模型复相关系数为0.997,因此该模型精度高,可以用来进行试油层产量预测。
| $ Y = - 6.6773 - 0.0033{X_1} + 0.3228{X_2} - 36.0132{X_3} + \\{\kern 42pt}0.0229{X_4} + 1.6152{X_5} + 71.5182{X_6} $ | (20) |
| 表2 多元回归模型自变量与因变量数据 Table 2 The independent variable and dependent variable data of multiple regression model |
利用建立的产量预测模型(式(20))回代验证,预测产量与原产量的相对误差最小为0.09%,最大为-11.08%,符合现场精度要求(<30%)。
3 模型对比研究利用表 1中的数据,建立试油层产量与6个静、动态参数的多元线性回归预测模型,该回归模型复相关系数为0.983,结果为
| $ Y = - 13.4268 + 0.0544h + 1.1304\Delta M - 17.0740\phi +\\{\kern 42pt} 0.0503{S_{\rm{o}}} + 0.8437K + 84.4718{v_{\rm{p}}} $ | (21) |
利用建立的多元非线性(式(20))和线性(式(21))产量预测模型回代验证,其试油层产量预测结果见表 3和图 1,可以看出非线性预测模型相对误差波动范围为-11.08%~7.09%,而线性模型范围为-52.93%~50.15%,因此非线性预测模型误差波动范围小,参数适应性强,预测结果更为准确。
| 表3 非线性模型与线性模型产量预测误差表 Table 3 The productivity prediction relative error of nonlinear and linear model |
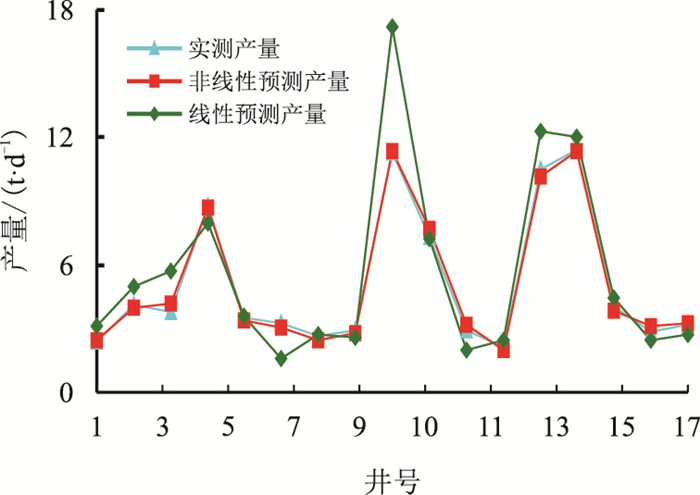 |
| 图1 非线性模型与线性模型预测产量对比 Fig. 1 The productivity prediction comparison of nonlinear and linear model |
(1) 通过研究多元线性回归和多元非线性回归原理,结合勘探开发实际情况,获得了利用多元非线性回归模型来预测试油层产量的方法。
(2) 研究的试油层多元非线性产量预测模型,综合考虑了产量与其影响参数的非线性关系,与常规模型对比,非线性模型适用性比线性模型更强,精度更高,模型回代验证相对误差最小为0.09%,最大为-11.08%。
(3) 将建立的多元非线性产量预测模型,应用于该勘探区块17口新井试油层产量预测,预测结果符合率为72.73%,误差小于30%。研究成果可为试油层措施改造提供科学依据,有效降低投资风险,提高勘探试油效益。
| [1] |
黄伏生, 赵永胜, 刘青年. 油田动态预测的一种新模型[J].
大庆石油地质与开发, 1987, 6 (4) : 55 –62.
Huang Fusheng, Zhao Yongsheng, Liu Qingnian. A new model for oilfield performance prediction[J]. Petroleum Geology and Oilfield Development in Daqing, 1987, 6 (4) : 55 –62. |
| [2] |
俞启泰. 七种递减曲线的特性研究[J].
新疆石油地质, 1994, 15 (1) : 49 –56.
Yu Qitai. A study of features for seven decline curves[J]. Xinjiang Petroleum Geology, 1994, 15 (1) : 49 –56. |
| [3] |
李社文. 应用广义伽马旋回模型预测油气田产量与可采储量[J].
石油勘探与开发, 1999, 26 (3) : 58 –61.
Li Shewen. Predicting the production and reserves of oil and gas fields by general model[J]. Petroleum Exploration and Development, 1999, 26 (3) : 58 –61. |
| [4] |
张虎俊. 预测油气田产量的Weng旋回及其参数求解方法[J].
断块油气田, 1997, 4 (3) : 25 –29.
Zhang Hujun. The Method for solving the parameters of Weng cycle to predict the production[J]. Fault-Block Oil and Gas Field, 1997, 4 (3) : 25 –29. |
| [5] |
袁自学, 陈元千. 预测油气田产量和可采储量的简易模型[J].
中国海上油气(地质), 1996, 10 (2) : 101 –105.
Yuan Zixue, Chen Yuanqian. A simple model for forecasting production and reserves of oil-gas fields[J]. China Offshore Oil and Gas (Geology), 1996, 10 (2) : 101 –105. |
| [6] |
邱先强, 李治平, 刘银山, 等. 致密气藏水平井产量预测及影响因素分析[J].
西南石油大学学报:自然科学版, 2013, 35 (2) : 141 –145.
Qiu Xianqiang, Li Zhiping, Liu Yinshan, et al. Analysis of productivity equation and influence factors of horizontal wells in tight sand gas reservoir[J]. Journal of Southwest Petroleum University:Science and Technology Edition, 2013, 35 (2) : 141 –145. |
| [7] | Li K, Horne R N. Prediction of oil production by gravity drainage[C]. SPE 84184, 2003. |
| [8] | 邢明海, 陈祥光, 王渝. 油田产量的多变量预测研究[J]. 油气田地面工程, 2005, 23 (10) : 16 –18. |
| [9] |
刘秀婷, 杨军, 程仲平, 等. 油田产量预测的新方法及其应用[J].
石油勘探与开发, 2002, 29 (4) : 74 –76.
Liu Xiuting, Yang Jun, Cheng Zhongping, et al. A new method of predicting oilfield output and its application[J]. Petroleum Exploration and Development, 2002, 29 (4) : 74 –76. |
| [10] | 中国科学院数学研究所统计组. 常用数理统计方法[M]. 北京: 科学出版社, 1979 . |
| [11] |
殷世荣, 宮健, 刘风喜, 等. 基础油的预测方法及应用[J].
油气地质与采收率, 2001, 8 (3) : 40 –42.
Yin Shirong, Gong Jian, Liu Fengxi, et al. Forecasting method of base oil and its application[J]. Petroleum geology and recovery efficiency, 2001, 8 (3) : 40 –42. |
| [12] |
谢祥俊, 贾闽惠, 杜志敏. 预测油气田产量的β模型[J].
西南石油学院学报, 2005, 27 (2) : 50 –52.
Xie Xiangjun, Jia Minhui, Du Zhimin. β model of predicting oilfield productivity[J]. Journal of Southwest Petroleum Institute, 2005, 27 (2) : 50 –52. |
| [13] |
刘志斌, 任宝生, 赵明. 基于时变系统的油田产量功能模拟预测[J].
西南石油大学学报:自然科学版, 2008, 29 (4) : 181 –184.
Liu Zhibin, Ren Baosheng, Zhao Ming. A functional simulation for oilfield output forecast based on time varying system[J]. Journal of Southwest Petroleum University:Science and Technology Edition, 2008, 29 (4) : 181 –184. |
| [14] |
霍进, 陈陆建, 王本成, 等. 储层伤害试井评价新方法研究[J].
西南石油大学学报:自然科学版, 2012, 34 (1) : 108 –114.
Huo Jin, Chen Lujian, Wang Bencheng, et al. Research on a new method of well testing analysis for formation damage evaluation[J]. Journal of Southwest Petroleum University (Science and Technology Edition), 2012, 34 (1) : 108 –114. |
| [15] |
王本成, 石国新, 路建国, 等. 考虑二次梯度的非线性双重介质渗流模型[J].
成都理工大学学报:自然科学版, 2011, 38 (2) : 140 –146.
Wang Bencheng, Shi Guoxin, Lu Jianguo, et al. Study on quadratic pressure gradient terms of the nonlinear filterding flow model in a dual medium reservoir[J]. Journal of Chengdu university of technology:Science and Technology Edition, 2011, 38 (2) : 140 –146. |
 2015, Vol. 37
2015, Vol. 37


