2. 中国石油东方地球物理勘探有限责任公司研究院, 河北 涿州 072750
2. Geophysical Research Institute, BGP, CNPC, Zhuozhou, Hebei 072750, China
对于海洋拖缆地震资料而言,受海水与空气的自由界面和海底影响,多次波异常发育。多次波严重压制了有效波能量,影响地震资料信噪比,影响速度分析、地震成像等方面,因此,多次波衰减成为拖缆海洋地震数据处理中的非常关键一步。拖揽海洋地震数据的多次波包括[1]:全程多次波,即受海底与自由界面影响形成的二次或多次反射多次波;部分多次波,如层间多次波,鸣震。
多次波类型不同,衰减方法也不同。马达海洋位于马达加斯加西海岸,其海水深度从几米到几千米,直接导致不同海水深度多次波的种类也不尽相同。图 1为该区块某一测线初始叠加剖面。可以看出,对于深层地震资料,也就是地震剖面的左侧,主要是与自由表面相关的长周期多次波;而浅层地震资料,地震剖面的右侧,主要是短周期的层间多次波。同时,深层多次波能量强,压制了有效波能量,其频率高于基底层位频率,出现频率倒挂现象。而浅层地震资料受层间多次波影响,基本无法分辨有效波与多次波,多次波影响非常严重。以上分析结果在单炮和速度分析能量谱上也得到了印证。
 |
| 图1 初始叠加剖面 Fig. 1 One line stack of raw data |
多次波压制方法多种多样[2],有利用多次波重复性和统计性的压制方法,如预测反褶积[3],中值滤波等;有利用多次波与一次波的正常时差差异来压制多次波的方法,如滤波、Radon变换[4]、聚束滤波[5]等;也有利用波动方程理论的多次波模型减去衰减方法[6],如波场外推法,反馈迭代法和SRME[7](与自由表面相关多次波衰减,Surface related Multiple Elimination)法等。
根据不同多次波的形成机制,本文采用SRME方法压制深层长周期多次波,采用预测反褶积方法压制层间多次波,然后通过Radon变换法衰减剩余多次波。实际处理结果表明,采用这种分步分段逐级衰减多次波的方法能够很好地压制多次波,提高资料信噪比。
1 方法原理 1.1 SRME法20世纪晚期,Verschuur D J等[7]提出利用SRME方法来压制与自由表面相关的多次波。该方法利用地震数据本身来预测多次波,而不需要地下介质的任何信息。Verschuur D J 等在文献[8-9]的基础上给出了海上二维采集的多次波预测公式
| ${M^{(n)}}(\omega, {x_\gamma }, {x_s}) = \sum\limits_{{x_k}} {P_0^{(n - 1)}(\omega, {x_\gamma }, {x_k})} \times P(\omega, {x_k}, {x_s})$ | (1) |
| $P_0^{(n)}(\omega, {x_\gamma }, {x_s}) = P(\omega, {x_k}, {x_s}) - A(\omega ){M^{(n)}}(\omega, {x_k}, {x_s})$ | (2) |
| $P_0^{(0)}(\omega, {x_\gamma }, {x_s}) = P(\omega, {x_\gamma }, {x_s})$ | (3) |
式中:
第1次迭代时,实际数据作为有效波被代入公式,实际地震数据和自身通过褶积运算就可以构成多次波;低阶次的多次波通过褶积运算可以构成高阶多次波。
这种方法实际是将地震记录中的与自由表面相关的多次波分解为若干个子反射。地震记录中的任何一个反射波同相轴都可以被认为是自由表面多次波的某个子反射(零阶多次波为有效波)。利用原始数据进行时空域褶积,根据数据一致性原理[10-11],不用考虑多次波在地下介质中的传播路径,将所有的子反射“褶积”在一起,再乘上自由表面反射系数$-1$,就能够模拟出自由表面多次波。
由式(1)可知,与自由表面相关的多次波其预测过程就是原始数据与本身沿着自由表面进行时间域和空间域褶积。根据数据一致性原理,对于某一炮检对地震道而言,分别从原始数据中抽取该炮点位置的共炮点道集和该检波点位置的共检波点道集,沿着自由表面将共炮点道集中的检波点位置与共检波点道集中的炮点位置相同的道进行搭配组合,然后将所有搭配组合的地震道两两进行褶积求和。即可预测出该炮检对地震道的与自由表面相关的多次波。利用以上方法,逐一预测每道自由表面多次波就能够得到整个地震数据的预测模拟的多次波。
有了预测出来的多次波,根据式(2),将多次波从原始地震数据中按照能量最小准则自适应的减掉,从而达到衰减多次波的目的。所以在实际应用中,首先模拟多次波,然后减去多次波。
根据以上方法原理,将海洋地震数据本身作为预测算子。在实际应用中为了更准确预测多次波,需要对原始海洋地震数据进行涌浪噪音和异常振幅去除,直达波切除等预处理;然后,对数据进行数据规则化,使炮集数据每道数据按固定偏移距增量从偏移距零处开始递增,以满足多次波模拟方法要求;应用球面扩散能量补偿,使地震数据振幅能均衡;进行SRME多次波模拟;反应用球面扩散能量补偿,使模拟出来的多次波与原始数据能量一致;进而以原始涌浪噪音衰减的数据作为参考,进行数据反规则化,使模拟出来的多次波地震数据与原始地震数据能够在偏移距范围上匹配一致;然后对模拟多次波与原始数据进行匹配滤波,包括振幅、频率、相位的匹配;最后以能量最小准则进行自适应相减,从而完成SRME衰减多次波处理。具体实现流程如图 2所示。
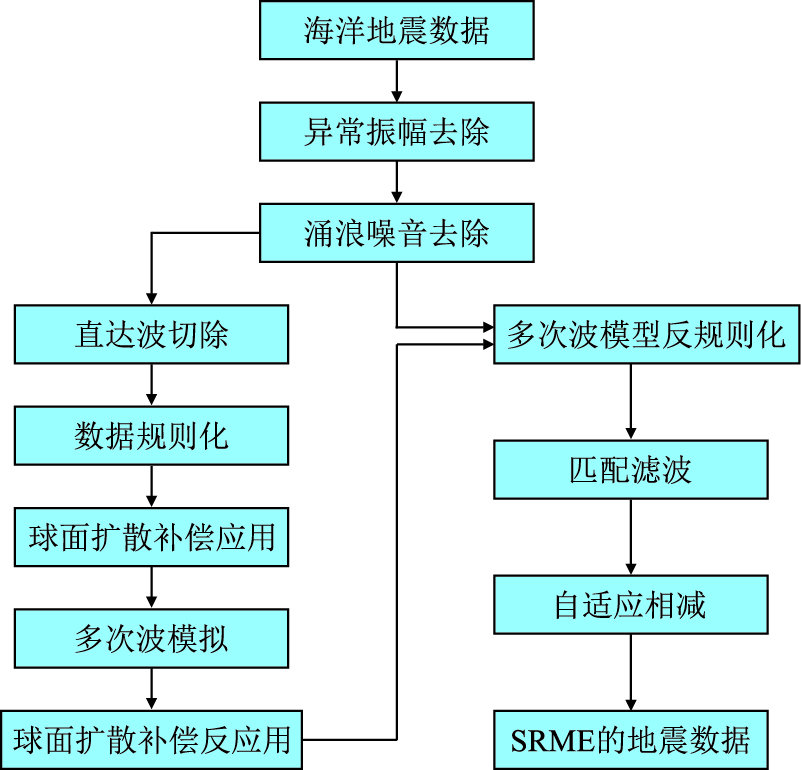 |
| 图2 SRME实现过程 Fig. 2 Process steps of SRME |
给定输入
假设地震记录满足反褶积的所有假设条件,则一个算子长度为$n$的预测滤波器和以$\alpha$为预测步长的情况的预测公式如下[3]
| $\left[ {\begin{array}{*{20}{c}} {{r_0}}&{{r_1}}&{{r_2}}& \cdots &{{r_{n - 1}}}\\ {{r_1}}&{{r_0}}&{{r_1}}& \cdots &{{r_{n - 2}}}\\ {{r_2}}&{{r_1}}&{{r_0}}& \cdots &{{r_{n - 3}}}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {{r_{n - 1}}}&{{r_{n - 2}}}&{{r_{n - 3}}}& \cdots &{{r_0}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{a_0}}\\ {{a_1}}\\ {{a_2}}\\ \vdots \\ {{a_{n - 1}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{r_\alpha }}\\ {{r_{\alpha + 1}}}\\ {{r_{\alpha + 2}}}\\ \vdots \\ {{r_{\alpha + n - 1}}} \end{array}} \right]$ | (4) |
式中:
根据公式4计算便可以预测出周期性的多次波,然后,通过预测误差滤波得到地震记录中的不可预测部分,即反射系数序列,从而达到预测反褶积将地震子波尖脉冲化和压制多次波的效果。
实际应用中,通过算子长度、预测步长扫描进行地震资料自相关处理。本区取算子长度200 ms,预测步长20 ms,结果表明,预测反褶积在交混回响和短周期多次波压制上效果明显,同时地震子波也得到了很好的压缩,提高了信噪比,拓宽了频带。
1.3 Radon变换法Radon变换方法基于时差滤波的方法压制多次波[12-14]。由于近偏移距的多次波动校时差和一次波动校时差差别不大,该法对近偏移距的多次波往往无能为力。考虑到抛物线路径对远炮检距反射同相轴能很好地近似,Radon 变换方式选择抛物线变换法。
抛物线Radon正变换公式为
| $v\left( {\tau, q} \right) = \int_{ - \infty }^\infty {u\left( {t = \tau + q{x^2}, x} \right)\textrm{d}x}$ | (5) |
其反变换公式为
| $u\left( {t, x} \right) = \int_{ - \infty }^\infty {v\left( {\tau = t - q{x^2}, q} \right)\textrm{d}q}$ | (6) |
式中:
根据式(5)和式(6),就可以采用滤波的方法达到衰减多次波的目的。具体实现过程为:首先拾取精确的一次波速度,将共中心点道集(CMP)进行动校正,那么一次波就拉成了水平直线同相轴,而多次波则处于欠动校状态,保持着近似抛物线的形态。将动校正后CMP道集转换到
根据以上方法原理,对马达区块海洋地震资料进行多次波噪音衰减。该区块海底深度范围较大,从几米到上千米,这就造成不同海水深度地震资料的多次波形成机制不同,因次,采用分步分段逐级衰减的方法来完成多次波压制,即SRME方法衰减与自由表面相关的多次波[15-20],预测反褶积方法衰减层间多次波,Radon变换法衰减剩余多次波。
首先以深海A测线CMP动校正道集进行效果分析,该处海底时间为3 500 ms,海底深度 约为2 600 m。图 3为远场子波反褶积、异常振幅和涌浪噪音衰减后的CMP动校正道集,可以看出动校正后7 400 ms以下存在很多欠动校正同相轴,通过其存在时间与海底时间关系确定其为与自由表面相关多次波,其能量比同一时间段有效波能量偏强,严重掩盖了有效波同相轴。
 |
| 图3 涌浪噪音衰减后的CMP动校正道集 Fig. 3 CMP gather after swell noise attenuation and NMO |
图 4为SRME后CMP动校正道集,可以看出图 3中的多次波得到了有效衰减,突出了有效波同相轴,提高了该时间段的信噪比。同时,可以发现其中远偏移距仍然存在多次波剩余。
 |
| 图4 SRME后的CMP动校正道集 Fig. 4 CMP gather after SRME and NMO |
图 5为预测反褶积后的CMP动校正道集,可以看出道集信噪比明显提高,但中远偏移距多次波剩余仍然存在。图 6为Radon 后的CMP动校正道集,可以看出中远偏移距多次波剩余得到有效衰减,多次波存在时间段信噪比得到很大提高,被多次波掩盖的有效波同相轴完全出露。通过对比图 3~图 6可以发现,SRME能够衰减大部分与自由表面相关多次波,但是存在小部分多次波剩余;预测反褶积能够提高地震资料信噪比,但是对与自由表面相关多次波衰减效果有限;Radon变换能够衰减剩余的小部分多次波,主要为远偏移距多次波,从而达到最大限度衰减多次波的目的。
 |
| 图5 预测反褶积后的CMP动校正道集 Fig. 5 CMP gather after predictive deconvolution and NMO |
 |
| 图6 Radon后的CMP动校正道集 Fig. 6 CMP gather after Radon and NMO |
图 7为图 3道集对应A测线的一段叠加剖面,即涌浪噪音衰减后的叠加剖面,图 8为图 4道集对应A测线的叠加剖面,即SRME后的叠加剖面,\mbox{图 9}为图 5道集对应A测线的叠加剖面,即预测反褶积后的叠加剖面,图 10为图 6道集对应A 测线的一段叠加剖面,即Radon后的叠加剖面。
 |
| 图7 A线涌浪噪音衰减后叠加剖面 Fig. 7 Stack section of line A after swell noise attenuation |
 |
| 图8 A线SRME后叠加剖面 Fig. 8 Stack section of line A after SRME |
 |
| 图9 A线预测反褶积后叠加剖面 Fig. 9 Stack section of line A after predictive deconvolution |
 |
| 图10 A线Radon后叠加剖面 Fig. 10 Stack section of line A after Radon |
通过对比可以发现,SRME衰减了大部分与海底相关多次波,使噪音段7 200 ms以下地震剖面信噪比得到很大的提高;预测反褶积压缩了地震子波,且地震剖面信噪比进一步得到提高;Radon变换衰减了剩余的中远偏移距多次波,使噪音段7 200 ms以下地震剖面信噪比信噪比进一步提高,由于Radon变换主要衰减了远偏移距多次波,所以其叠加剖面成像图 10相对于图 9变化主要表现在7 400 ms以下高频噪音背景的衰减。对比图 7与图 10可以发现,SRME、预测反褶积、Radon变换处理地震资料的多次波得到了很好地衰减,信噪比明显提高,成像更加清晰。以上对比分析结果表明,这种逐步逐级分段衰减多次波方法在深海海地震资料上能够获得较好的效果。
其次,对于浅层多次波,选取B测线叠加剖面加以分析,该测线海底深度从几米到上千米。图 11为B线涌浪噪音衰减后的叠加剖面,该图左侧主要为与自由表面相关的多次波,且其反射时间较深(大于2 700 ms),对有效波同相轴( 2 600 ms以上)影响较小;右侧主要为层间多次波,其影响范围很广,无法辨识真正的有效波和多次波。图 12为B线SRME处理后的叠加剖面,与图 11相比,左侧与自由表面相关多次波得到了很好地衰减,而右侧层间多次波衰减效果很弱,仍然存在很强的层间多次波。
 |
| 图11 B线涌浪噪音衰减后叠加剖面 Fig. 11 Stack section of line B after swell noise attenuation |
 |
| 图12 B线SRME后叠加剖面 Fig. 12 Stack section of line B after SRME |
 |
| 图13 B线预测反褶积后叠加剖面 Fig. 13 Stack section of line B after predictive deconvolution |
 |
| 图14 B线Radon后叠加剖面 Fig. 14 Stack section of line B after Radon |
图 13为B线预测反褶积处理后的叠加剖面,与图 12相比,该图左侧无明显变化,而右侧的层间多次波衰减效果明显,有效波层位清晰,提高了右侧地震资料的信噪比。图 14 为B 线Radon处理后的叠加剖面,与图 13相比,衰减了多次波剩余,进一步提高了信噪比,降低了深海部位深部高频噪音背景。对比图 11与图 14 可以发现,SRME、预测反褶积、Radon变换处理地震资料的多次波得到了很好地衰减,信噪比明显提高,成像更加清晰。以上结果表明,这种逐步逐级分段衰减多次波方法在浅海地震资料上也能够获得很好的衰减效果。
3 结语SRME方法能够很好地衰减与自由表面相关的多次波,预测反褶积方法能够很好地衰减层间多次波,抛物线Radon 变换法能够衰减剩余中、远偏移距的多次波,使多次波衰减的更加干净,成像效果更好。这种分步分段逐级衰减多次波的组合方法能够适应马达加斯加区块海底深度变换很大的特点,从而克服单一衰减方法无法完成整个区块多次波衰减任务的缺点。
这种组合方法使浅海和深海地震资料多次波都得到很好的压制,明显提高了地震资料的信噪比,为后续速度分析、叠前时间偏移、叠前深度偏移提供理想的基础资料。
| [1] | 朱广生, 陈传仁, 桂志先. 勘探地震学教程[M]. 武汉: 武汉大学出版社, 2005 . |
| [2] |
李鹏, 刘伊克, 常旭, 等. 多次波问题的研究进展[J].
地球物理学进展, 2006, 21 (3) : 888 –897.
Li Peng, Liu Yike, Chang Xu, et al. Progress on the multiple problems[J]. Progress in Geophysics, 2006, 21 (3) : 888 –897. |
| [3] | 渥·伊尔马兹. 地震数据处理[M]. 北京: 石油工业出版社, 1993 . |
| [4] | Foster D J, Mosher C C. Suppression of multiple reflection using the Radon transform[J]. Geophyiscs, 1992, 57 (3) : 386 –395. DOI:10.1190/1.1443253 |
| [5] |
胡天跃, 王润秋, 温书亮. 聚束滤波法消除海上地震资料的多次波[J].
石油地球物理勘探, 2002, 37 (1) : 18 –23.
Hu Tianyue, Wang Runqiu, Wen Shuliang. Multiple attenuation of seismic data from South China Sea by using beam-forming filtering method[J]. Oil Geophysical Prospecting, 2002, 37 (1) : 18 –23. |
| [6] |
牛滨华, 沈操, 黄新武. 波动方程多次波压制技术的进展[J].
地球物理学进展, 2002, 17 (3) : 480 –485.
Niu Binhua, Shen Cao, Huang Xinwu. Progress in multiple attenuation techniques based on wave equation[J]. Progress in Geophysics, 2002, 17 (3) : 480 –485. |
| [7] | Verschuur D J, Berkhout A J. Adaptive surface-related multiple elimination[J]. Geophysics, 1992, 57 (9) : 1166 –1177. DOI:10.1190/1.1443330 |
| [8] | Berkhout A J, Verschuur D J. Estimation of multiple scattering by iterative inversion, Part I:Theoretical considerations[J]. Geophysics, 1997, 62 (5) : 1586 –1595. DOI:10.1190/1.1444261 |
| [9] | Verschuur D J, Berkhout A J. Estimation of multiple scattering by iterative inversion, Part Ⅱ:Practical aspects and examples[J]. Geophysics, 1997, 62 (5) : 1596 –1611. DOI:10.1190/1.1444262 |
| [10] |
黄新武, 孙春岩, 牛滨华, 等. 基于数据一致性预测与压制自由表面多次波——理论研究与模型试验[J].
地球物理学报, 2005, 48 (1) : 173 –180.
Huang Xinwu, Sun Chunyan, Niu Binhua, et al. Surfacerelated multiple prediction and suppression based on dataconsistence:A theoretical study and test[J]. Chinese Journal of Geophysics, 2005, 48 (1) : 173 –180. |
| [11] |
黄新武, 牛滨华, 刘光, 等. 基于数据一致性原理预测与压制自由表面多次波的效果分析[J].
石油地球物理勘探, 2009, 44 (4) : 409 –416.
Huang Xinwu, Niu Binhua, Liu Guang, et al. Effect analysis of surface-related multiple prediction and suppression based on data-consistence[J]. Oil Geophysical Prospecting, 2009, 44 (4) : 409 –416. |
| [12] |
郭梦秋, 赵颜良, 左胜杰, 等. 海上地震资料处理中的组合压制多次波技术[J].
石油地球物理勘探, 2012, 47 (4) : 537 –544.
Guo Mengqiu, Zhao Yanliang, Zuo Shengjie, et al. Combined multiple attenuation in marine seismic data processing[J]. Oil Geophysical Prospecting, 2012, 47 (4) : 537 –544. |
| [13] |
张军华, 吕宁, 雷凌, 等. 抛物线拉冬变换消除多次波的应用要素分析[J].
石油地球物理勘探, 2004, 39 (4) : 398 –405.
Zhang Junhua, Lü Ning, Lei Ling, et al. Analysis of applied factors for using parabolic Radon transform to remove multiple[J]. Oil Geophysical Prospecting, 2004, 39 (4) : 398 –405. |
| [14] |
王建立, 王真理, 张洪宙, 等. 海上多次波的联合衰减法[J].
地球物理学进展, 2009, 24 (6) : 2070 –2078.
Wang Jianli, Wang Zhenli, Zhang Hongzhou, et al. A joint technique of Multiple attenuation for offshore seismic data processings[J]. Progress in Geophysics, 2009, 24 (6) : 2070 –2078. |
| [15] |
肖二莲, 陈瑜, 万欢, 等. SRME多次波衰减方法在海洋地震资料中的应用[J].
地球物理学进展, 2010, 25 (3) : 1057 –1064.
Xiao Erlian, Chen Yu, Wan Huan, et al. Surface-related multiple elimination on marine seismic data[J]. Progress in Geophysics, 2010, 25 (3) : 1057 –1064. |
| [16] |
赵秀莲, 陈茂根, 龚定康, 等. SRME技术在澳大利亚Timer Sea地区的应用[J].
海洋石油, 2009, 29 (4) : 48 –52.
Zhao Xiulian, Chen Maogen, Gong Dingkang, et al. Application of SRME on 2D seimic data from Timer Sea, Australia[J]. Offshore Oil, 2009, 29 (4) : 48 –52. |
| [17] |
王维红, 崔宝文, 刘洪. 表面多次波衰减的现状与进展[J].
地球物理学进展, 2007, 22 (1) : 156 –64.
Wang Weihong, Cui Baowen, Liu Hong. Research progress in surface-related multiple attenuation[J]. Progress in Geophysics, 2007, 22 (1) : 156 –64. |
| [18] |
黄兆林. SRME与Radon滤波方法组合衰减深水多次波[J].
工程地球物理学报, 2011, 8 (6) : 659 –665.
Huang Zhaolin. Multiple attenuation in deep water seismic exploration with combined aplication of SRME and Radon filtering[J]. Chinese Journal of Engineering Geophysics, 2011, 8 (6) : 659 –665. |
| [19] |
杨勇, 许云书, 张伟. 红海地区海洋地震资料处理效果[J].
石油地球物理勘探, 2008, 43 (S2) : 134 –137.
Yang Yong, Xu Yunshu, Zhang Wei. Offshore seismic data processing effect in Red Sea area[J]. Oil Geophysical Prospecting, 2008, 43 (S2) : 134 –137. |
| [20] |
李振勇, 姜浩, 李东升. 海洋地震数据处理技术探讨[J].
石油地球物理勘探, 2007, 42 (S1) : 8 –13.
Li Zhenyong, Jiang Hao, Li Dongsheng. Discussion on marine seismic data processing technique[J]. Oil Geophysical Prospecting, 2007, 42 (S1) : 8 –13. |
 2015, Vol. 37
2015, Vol. 37


