加快开发页岩气,对于缓解中国油气资源短缺具有重要意义。通常情况下,PDC钻头泥页岩地层的机械钻速是牙轮钻头的两倍[1]。然而,由于泥页岩中黏土矿物含量较高,当使用水基钻井液时,容易发生水化而具有黏性,且PDC钻头为整体式钻头,岩屑易黏附于切削齿和钻头体上形成泥包,严重影响PDC钻头的机械钻速[2]。
PDC钻头钻进性能的变化归根结底都源于切削齿与地层的相互作用[3]。利用单齿切削模型分析泥包对切削齿受力的影响,可以从根源上找到机械钻速下降的原因,为提高PDC钻头泥页岩地层钻进机械钻速提供理论依据。
现有的单齿切削模型考虑的因素不全,不适用于PDC钻头发生泥包的情况。有些模型未考虑围压,而围压对岩石强度、界面摩擦力、岩屑形状[4-5]具有重要影响;有些模型只考虑了切削面上的受力[6-9],这不符合切削齿具有倒角(倒角的存在对切削速度和钻压-扭矩比具有重要影响[3])以及切削齿后底面往往存在岩屑堆积(由于岩屑的反向流动[5])的实际情况(由于岩屑的反向流动,切削齿底面与该部分岩屑接触产生附加作用力[9]);还有些模型未考虑岩屑破碎带对切削齿受力的影响[6-9]。另外,绝大多数模型只涉及切削(岩屑生成)过程,而未包含岩屑运移、聚集过程分析[6-8],而离散单元模型表明已破碎岩屑的塑性变形消耗的能量远大于破碎完整岩石消耗的能量[10-11]。
本文建立的单齿切削模型全面考虑了围压、切削齿倒角面、切削齿后底面、切削齿表面岩屑破碎带等因素,利用该模型分析了泥包对破岩效率的影响规律,并提出了相应的对策。
1 数学模型 1.1 发生切削齿泥包时的模型Ⅰ模型建立的依据:高围压条件下钻进泥页岩地层时,随着切削过程的进行,“条带”状岩屑[4-5]长度增大而向前延伸,当岩屑超过一定长度或延伸受到钻头体阻碍时,“条带”状岩屑发生断裂,断裂的岩屑在“条带”状岩屑前作球状堆积,即发生了切削齿泥包[12-13]。
模型Ⅰ示意图如图 1所示,切削面上的力
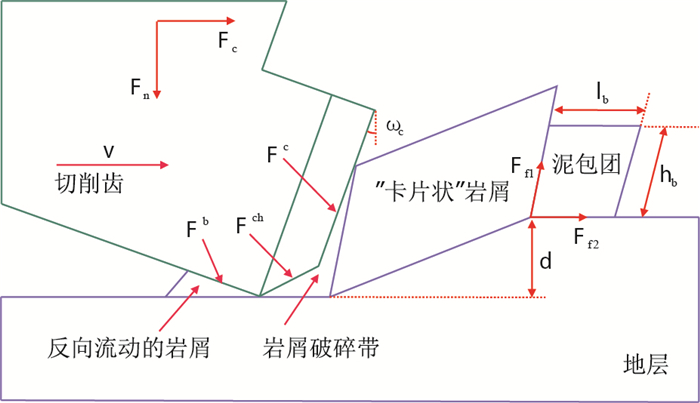 |
| 图1 模型Ⅰ示意图 Fig. 1 Sketch map of model Ⅰ |
由于泥包团分别与“卡片”状岩屑及原始地层之间的相对运动,产生了两个附加摩擦力
| $ {F_{{\rm{f}}1}} = \mu \left( {{p_{\rm{c}}}w{h_{\rm{b}}} + {F_{{\rm{f}}2}}\cos {\omega _{\rm{c}}}} \right) $ | (1) |
| $ {F_{{\rm{f}}2}} = \mu \left( {{p_{\rm{c}}}w{l_{\rm{b}}} + {F_{{\rm{f}}1}}\cos {\omega _{\rm{c}}}} \right) $ | (2) |
式中:
w-切削宽度,mm;
发生切削齿泥包时切削齿受到的切向力
| $ F_{\rm{c}} = F_{\rm{c}}^{\rm{c}} + F_{\rm{c}}^{{\rm{ch}}} + F_{\rm{c}}^{\rm{b}} + {F_{{\rm{f}}2}} + {F_{{\rm{f}}1}}\sin {\omega _{\rm{c}}} $ | (3) |
| $ F_{\rm{n}} = F_{\rm{n}}^{\rm{c}} + F_{\rm{n}}^{{\rm{ch}}} + F_{\rm{n}}^{\rm{b}} - {F_{{\rm{f}}1}}\cos {\omega _{\rm{c}}} $ | (4) |
式中:
模型建立的依据:“条带”状岩屑延伸过程中受到钻头体的阻碍并黏附于钻头体表面,随着切削过程的进行和岩屑的黏聚,岩屑被限制于钻头体和原始地层之间而无法排出。由于钻头的钻进,岩屑受到压实,造成钻头泥包。Smith J R[4]通过在切削齿上方设置一阻挡面的实验方法,模拟了钻头体对泥页岩岩屑运移的阻碍,观察到了严重的泥包现象。
发生钻头泥包时的单齿切削模型如图 2所示。
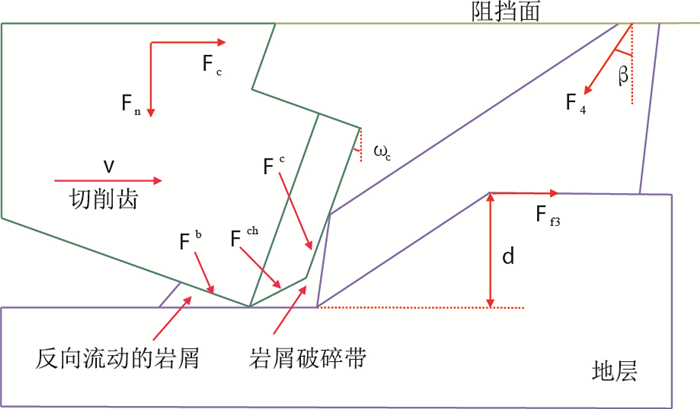 |
| 图2 模型Ⅱ示意图 Fig. 2 Sketch map of model Ⅱ |
岩屑与原始地层之间的摩擦力
| $ {F_{{\rm{f}}3}} = \mu{F_{4}}\cos {\beta} $ | (5) |
| $ {F_{4}} = {p_{\rm{CCS}}}{A_{4}} $ | (6) |
式中:
因此,发生钻头泥包时切削齿受到的切向力
| $ F_{\rm{c}} = F_{\rm{c}}^{\rm{c}} + F_{\rm{c}}^{{\rm{ch}}} + F_{\rm{c}}^{\rm{b}}{\rm{ - }}{F_4}\sin \beta + {F_{{\rm{f}}3}} $ | (7) |
| $ F_{\rm{n}} = F_{\rm{n}}^{\rm{c}} + F_{\rm{n}}^{{\rm{ch}}} + F_{\rm{n}}^{\rm{b}} + {F_4}\cos \beta $ | (8) |
Smith J R[4]利用Hughes Christensen公司的单齿切削试验装置进行了不同条件下的泥页岩单齿切削试验,本文利用其试验数据进行实例计算和模型验证。
(1)模型Ⅰ实例计算与模型验证
使用文献[4]中在清水环境下单齿(抛光锐齿)切削实验参数作为计算参数进行实例计算,实验过程中发生切削齿泥包,各计算参数如下:
| 表1 模型Ⅰ计算结果与试验值对比 Table 1 Comparison between computational values and experimental values of model Ⅰ |
表 1表明,模型I计算结果与试验值的相对误差均小于10%,平均相对误差为6.84%,误差在工程要求范围之内,从而证明了模型I计算结果的可靠性。
(2)模型Ⅱ实例计算与模型验证
使用文献[4]中分别在清水和矿物油环境中单齿(抛光锐齿)切削实验参数作为计算参数进行实例计算,实验过程中发生不同程度的钻头泥包,各计算参数如下:
| 表2 模型Ⅱ计算结果与试验值对比 Table 2 Comparison between computational values and experimental values of model Ⅱ |
表 2表明,模型模型Ⅱ计算结果与试验值的相对误差均小于10%,平均相对误差为6.18%,误差在工程要求范围之内,从而证明了模型Ⅱ计算结果的可靠性。
3 泥包对破岩效率的影响分析本文采用机械比能(MSE,Mechanical Specific Energy)作为表征破岩效率的指标,其定义为切削破碎单位体积岩石所消耗的能量[14],MSE与破岩效率成反比(式(9))。对于切削深度固定的单齿切削,轴向力做功为零
| $ {P_{{\rm{MSE}}}} = \dfrac{{{F_{\rm{c}}}}}{A} $ | (9) |
式中:
A-切削面积,mm2。
3.1 切削齿泥包对破岩效率的影响由前文中的分析可知,发生切削齿泥包时,由于泥包团分别与“卡片”状岩屑及原始地层之间的相对运动,产生了两个附加摩擦力
在前文所示的计算条件下,通过联立式(1)和式(2),计算得:
| $ {f_{{\rm{MSE}}}} = \frac{{\left| {\Delta F_1^{\rm{c}}} \right|{\rm{ /}}A}}{{\left( {{F_{\rm{c}}} - \Delta F_1^{\rm{c}}} \right){\rm{ /}}A}} = 46.85\% $ | (10) |
由此可见,在本文计算条件下,切削齿泥包的发生会使MSE增大46.85%,严重影响破岩效率。
由式(1)、式(2)、式(3)和式(9)可见,主要受
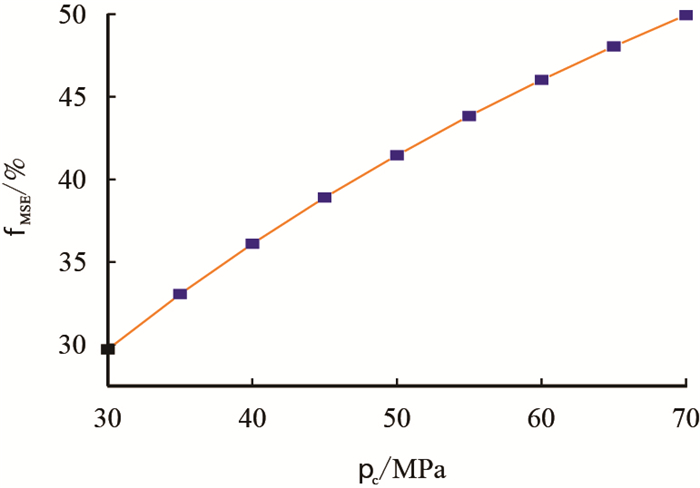 |
|
图3
|
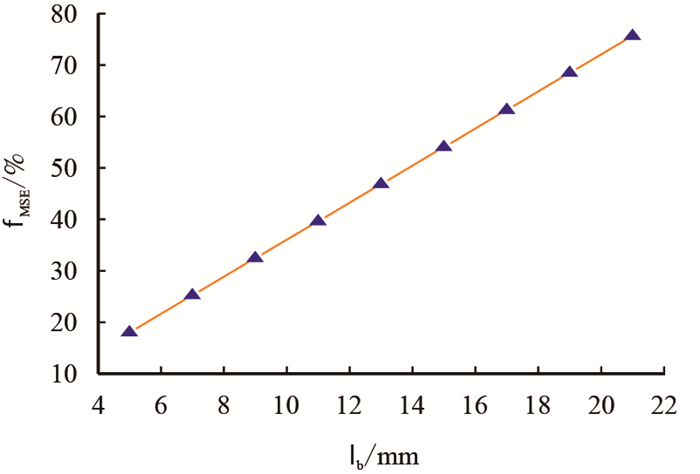 |
|
图4
|
由图 3和图 4可以看出,
由前文中的分析可知,发生钻头整体泥包时,受压实的岩屑在阻挡面上产生挤压力
在前文所示的计算条件下,通过式(5)和式(6)计算,
| $ {f_{{\rm{MSE}}}} = \frac{{\left| {\Delta F_2^{\rm{c}}} \right|{\rm{ /}}A}}{{\left( {{F_{\rm{c}}} - \Delta F_2^{\rm{c}}} \right){\rm{ /}}A}} = 73.13\% $ | (11) |
由此可见,在本文计算条件下,钻头泥包的发生会使MSE增大73.13%,严重影响破岩效率。
由式(5) 式(7)可知,
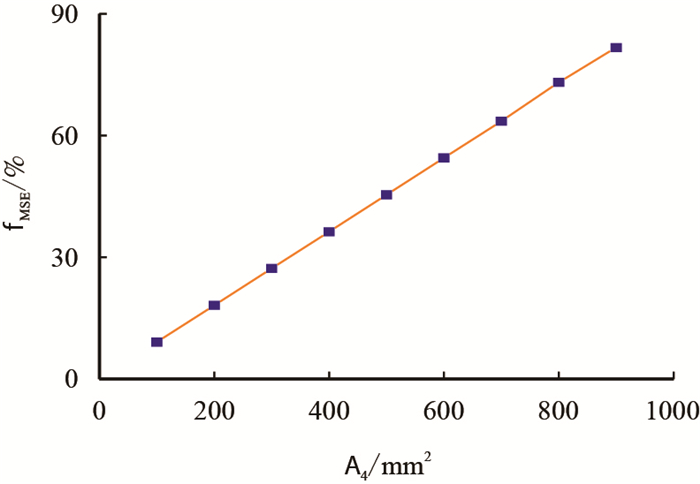 |
|
图5
|
图 5表明,
(1) 全面考虑了围压、切削齿倒角面、切削齿后底面、切削齿表面岩屑破碎带等因素,建立了PDC钻头分别发生切削齿泥包和钻头泥包时的单齿切削模型,实例计算验证了模型计算结果的可靠性。
(2) 切削齿泥包和钻头泥包均严重影响破岩效率,后者影响程度更大。
(3) 切削齿泥包中,围压和“泥包团”长度对破岩效率影响显著,破岩效率均随两者的增大而减小;钻头泥包中,泥包面积对破岩效率影响显著,破岩效率随泥包面积的增大而减小。
(4) 在实际钻井工程中,可以通过使用抑制水化较强的钻井液和密度较小的钻井液以降低泥包程度,提高破岩效率。
| [1] | Isbell M R,Scott D E,Freeman M A. Application-specific bit technology leads to improved performance in unconventional gas-shale plays[C]//IADC/SPE Drilling Conference and Exhibition, Society of Petroleum Engineers, 2010. |
| [2] | De Stefano G, Young S. The prevention and cure of bit balling in water based drilling fluids[C]//Offshore Mediterranean Conference and Exhibition, Offshore Mediterranean Conference, 2009. |
| [3] | Wells M, Marvel T, Beuershausen C. Bit balling mitigation in PDC bit design[C]//IADC/SPE Asia Pacific Drilling Technology Conference and Exhibition, Society of Petroleum Engineers, 2008. |
| [4] | Smith J R. Diagnosis of poor PDC bit performance in deep shales[D]. Louisiana:Louisiana State University and Agricultural & Mechanical College, 1998. |
| [5] | Ghoshouni M, Richard T. Effect of the back rake angle and groove geometry in rock cutting[C]//ISRM International Symposium-5th Asian Rock Mechanics Symposium, International Society for Rock Mechanics, 2008. |
| [6] | Seliami H, Fairhurst C, Deliac E, et al. The role of insitu rock stresses and mud pressure on the penetration rate of PDC bits[C]//ISRM International Symposium,International Society for Rock Mechanics, 1989. |
| [7] | Detournay E,Defourny P. A phenomenological model for the drilling action of drag bits[C]//International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, Pergamon, 1992, 29(1):13-23. |
| [8] | Glowka D A. Use of single-cutter data in the analysis of PDC bit designs:Part 1-development of a PDC cutting force model[J]. Journal of Petroleum Technology, 1989, 41 (8) : 797 –849. DOI:10.2118/15619-PA |
| [9] | Rahmani R, Smith J R, Taleghani A D. Analytical modeling of PDC single cutter-rock interaction under confining pressure[C]//46th US Rock Mechanics/Geomechanics Symposium, American Rock Mechanics Association, 2012. |
| [10] | Rafatian N, Miska S Z, Ledgerwood L W, et al. Experimental study of MSE of a single PDC cutter under simulated pressurized conditions[C]//SPE/IADC Drilling Conference and Exhibition, Society of Petroleum Engineers, 2009. |
| [11] | Ledgerwood Ⅲ L W. PFC modeling of rock cutting under high pressure conditions[C]//1st Canada-US Rock Mechanics Symposium, American Rock Mechanics Association, 2007. |
| [12] | Zijsling D H. Single cutter testing-a key for PDC bit development[C]//Offshore Europe, Society of Petroleum Engineers, 1987. |
| [13] | Warren T M, Sinor A. Drag bit performance modeling[C]//SPE Annual Technical Conference and Exhibition, Society of Petroleum Engineers, 1986. |
| [14] | Rajabov V, Miska S Z, Mortimer L, et al. The effects of back rake and side rake angles on mechanical specific energy of single PDC cutters with selected rocks at varying depth of cuts and confining pressures[C]//IADC/SPE Drilling Conference and Exhibition,Society of Petroleum Engineers, 2012. |
| [15] | Smith R H, Lund J B, Anderson M, et al. Drilling plastic formations using highly polished PDC cutters[C]//SPE Annual Technical Conference and Exhibition, Society of Petroleum Engineers, 1995. |
 2015, Vol. 37
2015, Vol. 37


