西南石油大学学报(自然科学版)  2015, Vol. 37 Issue (6): 151-157
引用本文
夏成宇, 孙巧雷, 冯定, 等 .区间分析法在精细注水管柱设计方面的应用[J]. 西南石油大学学报(自然科学版), 2015, 37(6): 151-157.
Xia Chengyu, Sun Qiaolei, Feng Ding, et al . Application of Interval Analysis Method in Design of Fine Water Flooding Injection String[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2015, 37(6): 151-157.
区间分析法在精细注水管柱设计方面的应用    [PDF全文]
夏成宇, 孙巧雷, 冯定 , 钱利勤, 施雷    
长江大学机械工程学院, 湖北 荆州 434023
收稿日期: 2013-09-02 ; 网络出版时间: 2015-11-10
基金项目: 国家自然科学基金(51275057,51405032);湖北省自然科学基金创新群体(2012FFA033)。
作者简介: 夏成宇,1981年生,男,汉族,讲师,主要从事管柱力学方面的研究。E-mail:qlq1010@126.com;
孙巧雷,1990年生,男,汉族,硕士研究生,主要从事管柱力学研究。E-mail:649647220@qq.com;
冯定,1963年生,男,汉族,教授,博士生导师,主要从事石油机械及井下工具的设计、诊断及动态仿真的理论与技术应用研究。E-mail:fengd@yangtzeu.edu.cn;
钱利勤,1982年生,女,汉族,讲师,主要从事管柱力学方面的研究。E-mail:441573083@qq.com;
施雷,1989年生,男,汉族,硕士研究生,主要从事管柱力学研究。E-mail:493857696@qq.com。
通信作者: 冯定, E-mail:fengd@yangtzeu.edu.cn
摘要: 随着油田开发进入中后期,油层及夹层的厚度越来越小,传统的大卡距大间距分层注水工艺管柱设计已经不能满足要求,为了提高采油效率,小卡距的精细分层注水工艺应运而生,然而此工艺具有卡封层数多和单层卡距小的特点,这对管柱力学量的精确计算提出了更高的要求。针对此问题,提出了一种区间分析法,考虑了管柱变形量的主要不确定因素,建立了三维不确定性管柱力学模型并得到了管柱变形量区间,最后结合现场数据对分析结果进行了验证,结果表明:现场数据与设计数据高度吻合,提高了注水合格率,对精细注水管柱的设计具有一定的指导意义。
关键词: 区间分析     不确定性     精细注水     管柱设计     精确计算    
Application of Interval Analysis Method in Design of Fine Water Flooding Injection String
Xia Chengyu, Sun Qiaolei, Feng Ding , Qian Liqin, Shi Lei    
School of Mechanical Engineering, Yangtze University, Jingzhou, Hubei 434023, China
Abstract: As the oilfield development enters the late period, the thickness of the reservoir and mezzanine becomes smaller and smaller and the traditional water injection technology is unable to meet the requirements of oilfield development. In order to enhance oil recovery, the fine layered water injection process comes into being. However this process possesses the characteristics of mass layers and short layer distance, which tends to bring difficulties to accurate calculation. For this reason, an interval analysis method is proposed in this paper,which takes into consideration the uncertain factors of string deformation and builds a three dimensional, uncertain model and figures out the deformation interval. In the end, the field data and calculation results are compared, as a result, both are highly identical and the qualified rate of water is improved distinctly, which will be of guiding significance for string designing.
Key words: interval analysis     uncertainty     fine water flooding     string design     precise calculation    
引 言

多层油藏注水开发中的一项关键技术就是要提高注入水的波及效率。对注水井而言，在同一压力系统下混合注水，某些层段大量进水，其余的层进水少甚至不进水，而不进水的油层段的原油难以驱替出来。因此，混合注水工艺越来越无法满足油藏精细注水的要求，影响油田开发效果，已经不能适应油田调整的需要。为了使各油层能按着配注量合理、均匀注水，以提高各油层的水驱油效率，小卡距小间距精细分层注水工艺[1-4]技术应运而生，并被国内外油田作为注水开发最有效的办法而广泛应用。精细分注水技术从过去的4段以下提高到7段、最多达10段，从最小卡距6.0 m缩小到0.7 m，从最小隔层1.0 m缩短到0.5 m。随着精细注水分注卡封层段增加和层间距缩小，如果弹性模量、管材的线膨胀系数、油套摩擦系数选取不合理，易导致设计封隔器不能坐封到指定位置或坐封在接箍上，使坐封失效，因此现场对注水管柱结构设计提出了更高要求。

近年来区间分析方法[5-9]是一种工程结构不确定性分析方法，区间分析方法在参数无法给定确定值或统计信息不足以描述不确定参数的概率分布或隶属函数，工程单位仅提供不确定参数的区间范围的情况下，就能够确定结构响应的区间范围。由于油田现场无法提供确切的油管弹性模量、管材线膨胀系数、油套摩擦系数等参数，只能提供大致区间范围。本文利用区间分析方法，考虑了弹性模量、管材的线膨胀系数、油套摩擦系数分析等不确定因数对注水管柱力学和变形量影响，建立了不确定性三维管柱力学模型，计算坐封工况注水管柱变形量的区间范围，在此基础上注水管柱结构进行设计。

1 区间分析法 1.1 区间数

(1) 定义

设$\left( {{\boldsymbol{S}}, \leqslant } \right)$为偏序集，对给定数对$\left( {{x^ - }, {x^ + }} \right)$，若满足${x^ - }, {x^ + } \in {\boldsymbol{S}}$，且${x^ - } \leqslant {x^ + }$，则可定义一个区间数X[1]。

(2) 四则运算

设两区间数$X = \left[{{x^-}, {x^ + }} \right]，Y= \left[{{y^-}, {y^ + }} \right]$，有

$ X + Y = \left[{{x^-} + {y^-}, {x^ + } + {y^ + }} \right] $ (1)
$ X - Y = \left[{{x^-}-{y^-}, {x^ + } - {y^ + }} \right] $ (2)
$ X*Y = \left[\begin{array}{l} \min \left( {{x^-}{y^-}, {x^-}{y^ + }, {x^ + }{y^ - }, {x^ + }{y^ + }} \right), \\ \max \left( {{x^ - }{y^ - }, {x^ - }{y^ + }, {x^ + }{y^ - }, {x^ + }{y^ + }} \right) \end{array} \right] $ (3)
$ X/Y = X*\left (1/Y \right ) = \left[{{x^-}, {x^ + }} \right]*\left[{1/{y^ + }, 1/{y^-}} \right] $ (4)
1.2 管柱力学中主要不确定参数

精细注水分注卡封层段增加和层间距缩小，对管柱下入后管柱的变形量计算结果精确性要求更加严格，而油管弹性模量、管材的线膨胀系数、油套摩擦系数等参数分析选取不同，导致变形量计算结果不同，因此选取油管弹性模量、管材的线膨胀系数、油套摩擦系数不确定参数。

(1) 油管弹性模量的不确定性。由每根油管弹性模型有差异且在使用过程中不断降低，因此很难用确定值表示油管的弹性模量，现场只能根据油管的使用情况给定大致区间。根据现场使用情况采用区间数表示油管弹性模量为

$ E = \left[{{E^-}, {E^ + }} \right] $ (5)

式中： ${E^ - }$-油管弹性模量最小值，GPa；${E^ + }$-油管弹性模量最大值，GPa。

(2) 油管线膨胀系数、油套摩擦系数的不确定性。与油管弹性模量不确定性相似，采用区间数表示油管的线膨胀系数、油套摩擦系数分别为

$ \alpha ' = \left[{{{\alpha '}^-}, {{\alpha '}^ + }} \right] $ (6)
$ {\mu '} = \left[{{\mu ^-}, {\mu _{}}^ + } \right] $ (7)

式中： ${{\alpha '}^ - }$-油管线膨胀系数最小值，℃-1；${{\alpha '}^ + }$-油管线膨胀系数最大值，℃-1；${{\mu}^ - }$-油管摩擦系数最小值，无因次；${{\mu}^ + }$-油管摩擦系数最大值，无因次。

2 管柱三维管柱力学不确定性模型

在文献[10]~文献[13]三维管柱刚性力学模型基础上，并引入区间分析法建立不确定三维管柱力学模型，分析管柱受力及变形分析。

2.1 管柱力学理论计算模型

取自然坐标系(${\boldsymbol{T}}，{\boldsymbol{B}}，{\boldsymbol{N}}$)，假定管柱完全受井眼的限制，认为管柱中心线与井眼中心线一致。在井眼弯曲井段取任一微元段AB，并对其进行受力分析。以A为起始点，B为终点坐标，曲线坐标为s；微元的坐标为$s+{\rm{d}}s$，微元段的受力如图 1所示，假定挠率为0，则${M_{\rm{n}}}\left( s \right) = 0$，计算模型为

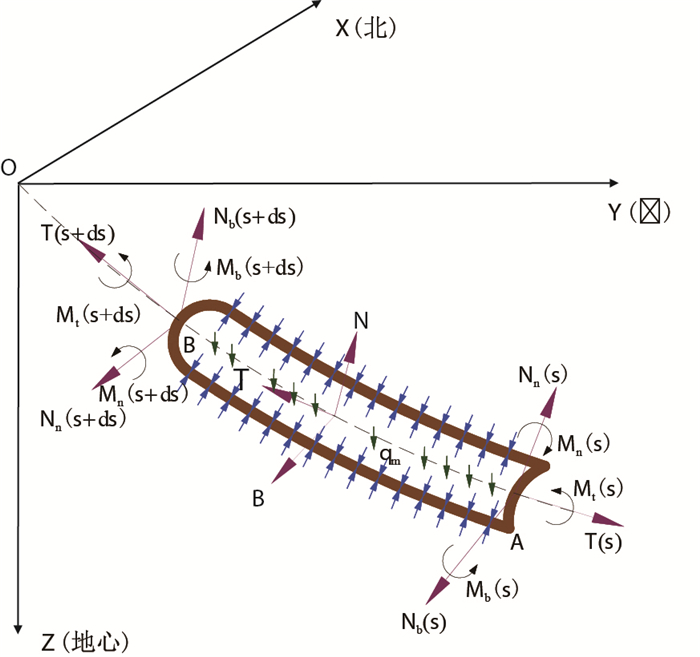图1 微元段的受力示意图 Fig. 1 The force sketch of unit
$ \left\{ \begin{array}{l} \dfrac{{{\rm{d}}T}}{{{\rm{d}}s}} = - K \cdot \dfrac{{{\rm{d}}M_{\rm{b}}(s)}}{{{\rm{d}}s}} - \left( { \pm {\mu _{\rm{\alpha }}}N} \right) + {q_{\rm{m}}}{K_{\rm{f}}}\cos \alpha \\[6pt] \dfrac{{{\rm{d}}{M_{\rm{t}}}}}{{{\rm{d}}s}} = {\mu _{\rm{t}}}RN\\[6pt] \dfrac{{{{\rm{d}}^2}M_{\rm{b}}(s)}}{{{\rm{d}}{s^2}}} = KT + {N_{\rm{n}}} - {q_{\rm{m}}}{K_{\rm{f}}}\sin \alpha \dfrac{{{K_{\rm{\alpha }}}}}{K}\\[6pt] K\dfrac{{{\rm{d}}{M_{\rm{t}}}}}{{{\rm{d}}s}} = {N_{\rm{b}}} - {q_{\rm{m}}}{K_{\rm{f}}}{\sin ^2}\alpha \dfrac{{{K_{\rm{\varphi }}}}}{K}\\[6pt] {N^2} = N_{\rm{n}}^2 + N_{\rm{b}}^2 \\[6pt] {M_{\rm{b}}\left( s \right) = E_{\rm{I}}K} \end{array} \right. $ (8)

式中：

T-管柱有效轴向力，kN；s-井深，m；K-井眼曲率，rad/m；${M_{\rm{b}}}$-副法线方向的弯矩，kN·m；${E_{\rm{I}}}$-管柱的弯曲刚度，kN·m2；$\mu _{\rm{\alpha}}$-轴向摩擦系数，无因次；N-管柱与井壁之间的接触正压力，kN；$q_{\rm{m}}$-单位长度管柱的浮重，kN/m；$K_{\rm{f}}$-浮力系数，无因次；$\alpha$-井斜角，rad；$M_{\rm{t}}$-管柱所受扭矩，kN·m；$\mu _{\rm{t}}$-周向摩擦系数，无因次；R-油管外径于内径的比值，无因次；$N_{\rm{n}}$-主法线法向与井壁的接触压力，kN；$K_{\rm{\alpha}}$-井斜变化率，rad/m；$N_{\rm{b}}$-副法线法向与井壁的接触压力，kN；$K_{\rm{\varphi}}$-方位角变化率，rad/m。

式(8)为非线性方程组，采用解非线性方程组的拟牛顿迭代法进行求解，选用有限差分中的差分公式

$ \left\{ \begin{array}{l} \dfrac{{{\rm{d}}T}}{{{\rm{d}}s}} = \dfrac{{T(s + 1) - T(s)}}{{h(s + 1) - h(s)}}\\[6pt] \dfrac{{{\rm{d}}{M_{\rm{t}}}}}{{{\rm{d}}s}} = \dfrac{{{M_{\rm{t}}}(s + 1) - {M_{\rm{t}}}(s)}}{{h(s + 1) - h(s)}}\\[6pt] \dfrac{{{\rm{d}}K}}{{{\rm{d}}s}} = \dfrac{{K(s + 1) - K(s)}}{{h(s + 1) - h(s)}}\\[6pt] \dfrac{{{{\rm{d}}^2}K}}{{{\rm{d}}{s^2}}} = \dfrac{{K(s + 2) - 2K(s + 1) + K}}{{{{\left [h(s + 1)-h(s) \right]}^2}}} \end{array} \right. $ (9)

式中：h-计算段的段长，m。

用式(9)将微分方程离散化，代入非线性方程组求解，即可计算出管柱各计算点处的摩阻力、摩擦扭矩以及轴向载荷。

2.2 管柱力学计算模型引入区间分析法

根据区间分析法四则运算法则，联合式(8)、式(9)得到三维管柱力学不确定性模型

$ \left\{ \begin{array}{l} \dfrac{{T(s + 1) - T(s)}}{{h(s + 1) - h(s)}} = - K(s) \cdot \left[{{E^-}, {E^ + }} \right]I\dfrac{{K(s + 1) - K(s)}}{{h(s + 1) - h(s)}} - \left( { \pm \left[{{\mu _\alpha }^-, {\mu _\alpha }^ + } \right]N} \right) + {q_{\rm{m}}}{K_{\rm{f}}}\cos \alpha \\[6pt] \dfrac{{{M_{\rm{t}}}(s + 1) - {M_{\rm{t}}}(s)}}{{h(s + 1) - h(s)}} = \left[{{\mu _{\rm{t}}}^-, {\mu _{\rm{t}}}^ + } \right]RN\\[6pt] \dfrac{{K(s + 2) - 2K(s + 1) + K(s)}}{{{{[h(s + 1)-h(s)]}^2}}} = \left( {K(s)T + {N_{\rm{n}}} - {q_{\rm{m}}}{k_{\rm{f}}}\sin \alpha \dfrac{{{K_\alpha }}}{{K(s)}}} \right) \cdot \left[{1/{E^-}, 1/{E^ + }} \right]/I\\[6pt] \dfrac{{{M_{\rm{t}}}(s + 1) - {M_{\rm{t}}}(s)}}{{h(s + 1) - h(s)}} = {N_{\rm{b}}}/K(s) - {q_{\rm{m}}}{k_{\rm{f}}}{\sin ^2}\alpha \dfrac{{{K_\varphi }}}{{K{{(s)}^2}}}\\[6pt] {N^2} = N_{\rm{n}}^2 + N_{\rm{b}}^2 \end{array} \right. $ (10)

式中：I-管柱的惯性矩，m4。

2.3 管柱的变形量区间计算

由于管柱在自重、封隔器层间压差、温度变化等因素影响下，会发生较明显的轴向变形。考虑弹性模量、管材的线膨胀系数、油套摩擦系数不确定影响下，由区间分析法分析计算胡克定律效应、活塞效应、鼓胀效应、温度效应、螺旋弯曲效应、黏滞摩阻效应等基本效应的变形区间[14-20]。

(1) 胡克定律效应。确定轴向载荷作用下，管柱的变形量区间为

$ \Delta L_{\rm{h}}^{\rm{F}} = \dfrac{{4\left[{{T^-}, {T^ + }} \right]L \times {{10}^{ - 3}}}}{{\pi ({{D}^2} - {{d}^2})}} \cdot \left[{1/{E^ + }, 1/{E^-}} \right] = \\[6pt] {\kern 42pt} \dfrac{{4L \times {{10}^{ - 3}}}}{{\pi ({D^2} - {d^2})}} \cdot \left[{{T^-}/{E^ + }, {T^ + }/{E^-}} \right] $ (11)

式中：$\Delta L_{\rm{h}}^{\rm{F}}$-管柱的变形量区间，m；

D-管柱的外径，m；

d-管柱的内径，m；

L-管柱长度，m。

(2) 活塞效应。活塞力作用下管柱轴向变形量区间为

$ \Delta {L_{\rm{h}}} = \dfrac{{{F_{\rm{p}}}}}{{EA}} = \dfrac{{L \times {{10}^{ - 3}}}}{A} \left[{1/{E^-}, 1/{E^ + }} \right]\cdot\\[6pt] {\kern 42pt}\left[{{A_{\rm{p}}}{p_{\rm{d}}}-\left( {{A_{\rm{p}}}-{A_{\rm{o}}}} \right){p_{\rm{u}}}-{A_{\rm{i}}}{p_{\rm{i}}}} \right] $ (12)

式中：

$\Delta {L_{\rm{h}}}$-活塞力下管柱轴向变形量区间，m；

${F_{\rm{p}}}$-活塞力，kN；

E-管材弹性模量，MPa；

A-油管壁截面积，m2；

${A_{\rm{p}}}$-井眼内截面积，m2；

${p_{\rm{d}}}$-封隔器下部环空压力，MPa；

${A_{\rm{o}}}$-油管外截面积，m2；

${p_{\rm{u}}}$-封隔器上部环空压力，MPa；

${A_{\rm{i}}}$-油管内腔截面积，m2；

${p_{\rm{i}}}$-油管内压力，MPa。

(3) 温度效应。由于井筒温度变化所引起的管柱轴向变形称之为温度效应，管柱受冷会缩短，受热会伸长。温度效应引起的轴向变形量区间

$ \Delta {L_{\rm{w}}} = \left[{{{\alpha '}^-}, {{\alpha '}^ + }} \right] \cdot L\Delta t $ (13)

式中：$\Delta {L_{\rm{w}}}$-温度效应引起的轴向变形量区间，m；

$\Delta t$-温度差，℃。

(4) 鼓胀效应。管柱由于内外压力差产生的管柱伸长或缩短现象，称之为鼓胀效应，其引起轴向变形量区间为

$ \Delta {L_{\rm{g}}} = \dfrac{{2\gamma \left( {\Delta {p_{\rm{i}}}{d^2} - \Delta {p_{\rm{o}}}{D^2}} \right)}}{{\left( {{D^2} - {d^2}} \right)}}L \cdot \left[{1/{E^-}, 1/{E^ + }} \right] $ (14)

式中：$\Delta {L_{\rm{g}}}$-鼓胀效应引起的轴向变形量区间，m；

$\Delta {p_{\rm{i}}}$-油管内压差，MPa；

$\Delta {p_{\rm{o}}}$-油管外压差，MPa。

(5) 螺旋弯曲效应。当管柱的轴向力大于螺旋屈曲临界载荷时，管柱将发生屈曲失稳，弯曲井段发生螺旋弯曲变形量区间为

$ \Delta {L_{\rm{h}}} = \dfrac{{\left[{{T^-}, {T^ + }} \right]r_{\rm{c}}^2}}{{4I}}L{}_{\rm{h}} \cdot \left[{1/{E^ + }, 1/{E^-}} \right] = \\{\kern 42pt} \left[{{T^-}/{E^ + }, {T^ + }/{E^-}} \right]\dfrac{{L{}_{\rm{h}}r_{\rm{c}}^2}}{{4I}} $ (15)

式中：$\Delta {L_{\rm{h}}}$-螺旋弯曲变形量区间，m；

${T^ - }$-最小轴向力，kN；

${T^ + }$-最大轴向力，kN；

${r_{\rm{c}}}$-井眼和管柱之间的环空间隙，m；

${L_{\rm{h}}}$-螺旋屈曲段长度，m。

(6) 黏滞摩阻效应。管内流体流动过程中会受到管壁摩擦阻力，反之对管柱产生相应的反作用力。在黏滞摩阻的作用下，管柱变形量区间为

$ \Delta {L_\lambda } = \dfrac{{{h_\lambda }{\rho _{\rm{m}}}{\rm{g}}\pi {d^2}L}}{A} \cdot \left[{1/{E^-}, 1/{E^ + }} \right] $ (16)

式中：$\Delta {L_{\lambda}}$-黏滞摩阻引起的管柱变形量区间，m；

${h_{\lambda}}$-沿程水头损失，m；

${\rho _{\rm{m}}}$-流体的密度，kg/m3；

g-重力加速度，g = 9.81 m/s2。

注水管柱总变形量轴向变形量区间

$ \Delta L = \Delta L_{\rm{h}}^{\rm{F}} + \Delta {L_{\rm{h}}} + \Delta {L_{\rm{w}}} + \Delta {L_{\rm{g}}} + \Delta {L_{\rm{h}}} + \Delta {L_{\rm{\lambda }}} $ (17)

式中：$\Delta L$-总变形量区间，m。

3 管柱串结构区间设计方法 3.1 封隔器坐封区间确定

如图(2)所示的注水工艺封隔器坐封位置，要求封隔器必须有效封隔指定的射孔段且封隔器不能压在接箍上。则确定封隔器最优坐封区间为

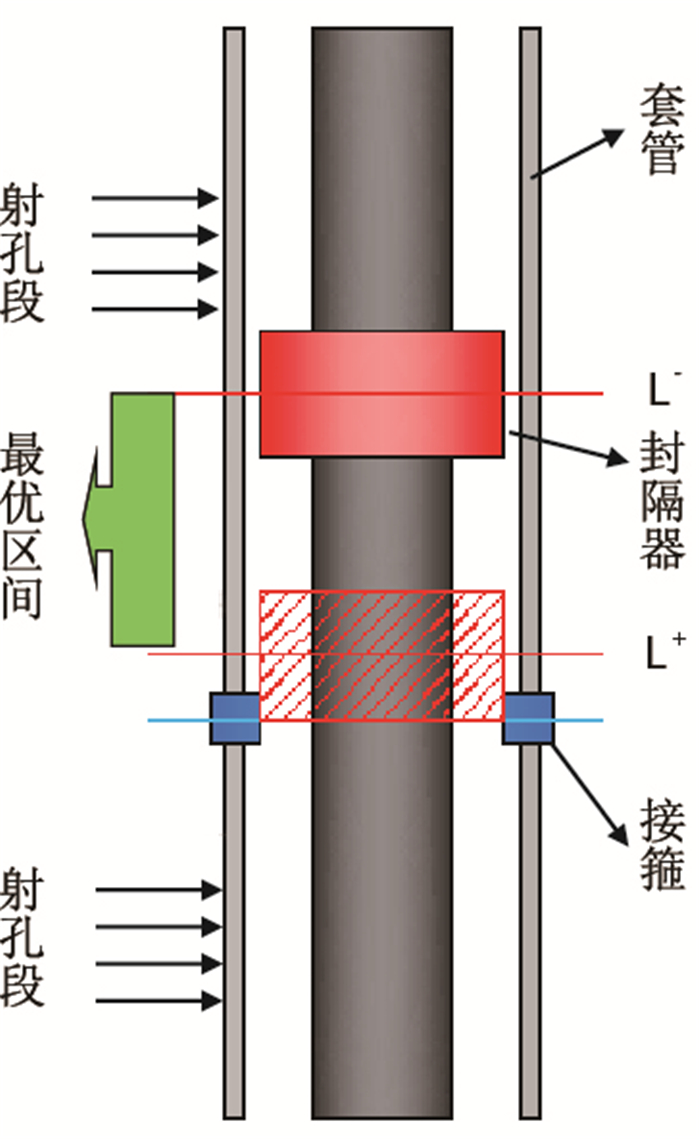图2 封隔器坐封位置示意图 Fig. 2 The position of packer setting
$ {L_0} = \left[{{L^-}, {L^ + }} \right] $ (18)

式中：

$L_0$-封隔器最优坐封区间，m；

${L^{-}}$-油封隔器坐封上端位置，m；

${L^{+}}$-封隔器坐封下端位置，m。

3.2 管柱结构设计计算

由式(17)计算管柱的变形量区间为

$ \Delta L = \left[{\Delta {L^-}, \Delta {L^ + }} \right] $ (19)

式中：$\Delta{L^{-}}$-管柱变形最小值，m；

$\Delta{L^{+}}$-管柱变形最大值，m。

坐封后地面测得下入油管长度加上油管伸长量在封隔器最优区间内，则满足要求，有

$ {L^ - } \leqslant \Delta {L^ - } + L \leqslant \Delta {L^ + } + L \leqslant {L^ + } $ (20)
4 实例分析 4.1 基本参数

某油田6层精细注水管柱设计，该井固井质量合格，最大井斜33°，最大方位角42.61°；人工井底1 868.6 m，水泥返高98.0 m，套管下深1 881.6 m；套管接箍位置分别为1 724.87，1 727.31，1 737.57，1 747.64，1 757.72，1 778.09，1 767.92，1 788.73，1 798.74，1 809.28，1 819.4，1 829.47，1 839.6，1 849.72，1 860.03，1 871.12，1 881.18，1 881.57 m；套补距2.7 m；套管钢级为J55。井斜数据见表 1，其层及射孔段数据见表 2。

表1 井斜数据表 Table 1 The data of well deviation
表2 油层及射孔段数据 Table 2 The data of reservoir and perforated interval
4.2 管柱结构设计分析

(1) 坐封工况不同弹性模量油管变形量计算

计算参数：坐封压力15 MPa，弹性模量2.06×105 MPa，油套摩擦系数0.02；线胀系数0.000 012 ℃-1；油管线重9.17 kg/m；注入液密度1 000 kg/m3，可选择封隔为Y344、Y341或K344。

分别计算当油管弹性模量为E、0.95E、0.90E、0.85E、0.80E时，坐封工况油管的变形量随井深变化规律如图 3，随着弹性模量的降低变形量增加，弹性模量为E和0.80E时变形量误差达到0.25 m，可见油管弹性模量对油管的变形量影响很大。根据油田现场情况确定弹性模量、油套摩擦系数、线胀系数参数的不确定区间分别为[0.8, 1.0]E，[0.9, 1.0]α，[0.85, 1.0]μ；井深为1 600 m时计算油管变形量区间随井升变化区间见图 4。

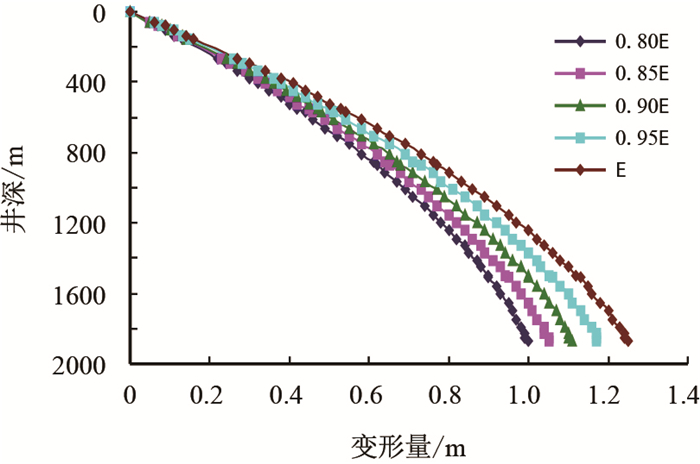图3 不同弹性模量下油管变形量随井深变化规律 Fig. 3 The relationship between tubing deformation section and well deep in different elasticity modulus
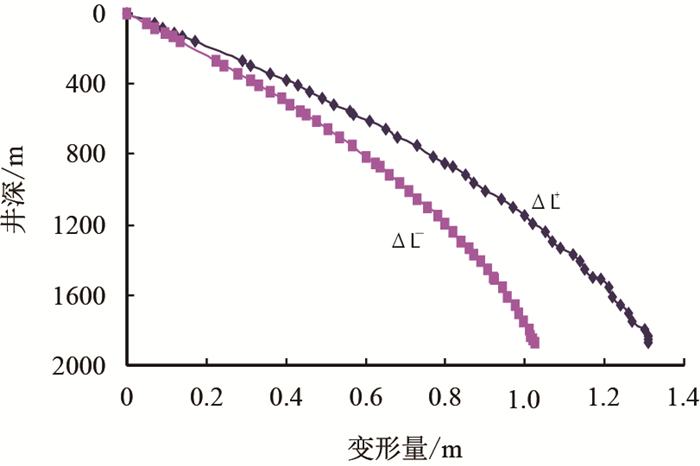图4 油管变形量区间随井深变化规律 Fig. 4 The relationship between tubing deformation section and well deep

(2) 管柱结构设计

由模态搜索法得出了管柱6个封隔器的下放区间和优选取值(表 3)，根据计算数据，设计管柱结构见图 5，该设计通过了现场测试。

表3 封隔器下放区间表 Table 3 The data table of tubing set position
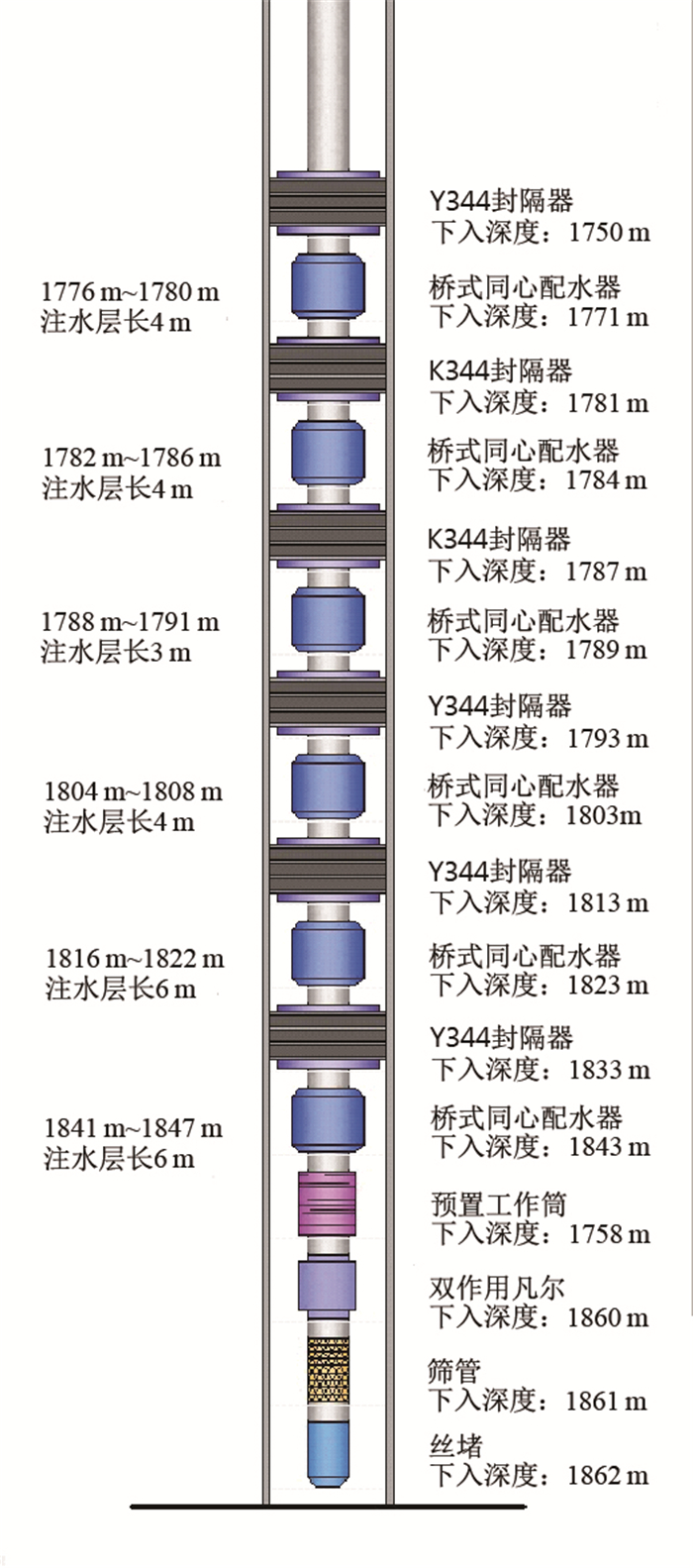图5 管柱结构设计图 Fig. 5 The design sketch of string
5 结 论

(1) 综合考虑注水管柱中不确定参数影响下，建立了注水管柱力学不确定模型，并提出了管柱变形量区间计算方法。

(2) 考虑射孔段和接箍影响确定封隔器坐封最优坐封区间，考虑了不确定影响因素，提出了计算管柱设计区间分析方法。

(3) 现场50口管柱设计数据全部在本文方法计算设计区间内，表明本方法正确可行。

参考文献
[1] 李海方, 单璐瑶. 利用细分注水调整方法有效改善油田开发效果[J]. 内蒙古石油化工, 2010, 36 (12) : 153 –158.
[2] 牟汉兵, 闫海霞, 夏廷仪, 等. 张店油田精细注水实践与认识[J]. 石油天然气学报, 2010, 32 (2) : 345 –348.
[3] 邹金光, 王家明. 全自动高效精细注水过滤系统[J]. 石油机械, 1990, 18 (12) : 46 –47.
[4] 梁鹏. 水驱油田精细注水结构调整稳产措施研究与探讨[J]. 装备制造, 2010 (1) : 98 .
[5] 郭书祥, 吕震宙. 区间运算和静力区间有限元[J]. 应用数学和力学, 2001, 22 (12) : 1249 –1254.
[6] Mcwilliam S. Anti-optimisation of uncertain structures using interval analysis[J]. Computers & Structures, 2001, 79 (4) : 421 –430.
[7] 郭书样, 吕震宙, 冯元生. 基于区间分析的结构非概率可靠性模型[J]. 计算力学学报, 2001, 18 (1) : 56 –60.
[8] 王光远. 论不确定性结构力学的发展[J]. 力学进展, 2002, 32 (2) : 205 –211.
Wang Guangyuan. On the development of uncertain structural mechanics[J]. Advances In Mechanics, 2002, 32 (2) : 205 –211.
[9] 肖峻, 王成山, 罗凤章. 区间层次分析法的权重求解方法初探[J]. 系统工程与电子技术, 2005, 26 (11) : 1597 –1600.
Xiao Jun, Wang Chengshan, Luo Fengzhang. Exploration on the methods of weight calculation in the interval based AHP[J]. Systems Engineering and Electronics, 2005, 26 (11) : 1597 –1600.
[10] 刘清友, 孟庆华, 庞东晓. 钻井系统动力学仿真研究及应用[M]. 北京: 科学出版社, 2009 .
[11] Ho H S. An improved modeling program for computing the torque and drag in directional and deep wells[C]. SPE 18047, 1988.
[12] 李子丰, 蔡雨田, 李冬梅, 等. 地层测试管柱力学分析[J]. 石油学报, 2011, 32 (4) : 709 –716.
Li Zifeng, Cai Yutian, Li Dongmei, et al. Mechanical analysis of pipe string in formation testing[J]. Acta Petrolei Sinica, 2011, 32 (4) : 709 –716.
[13] 李子丰, 孙虎, 苏金柱, 等. 压裂管柱力学分析理论与应用[J]. 应用基础与工程科学学报, 2012, 20 (5) : 846 –862.
Li Zifeng, Sun Hu, Su Jinzhu, et al. Theory and applications of mechanical analysis of tubing string in fracturing operation[J]. Journal of Basic Science and Engineering, 2012, 20 (5) : 846 –862.
[14] 刘小光. 水平井分层注水管柱受力分析研究[D]. 青岛: 中国石油大学(华东), 2011.
[15] 杨魁. 同井注采封隔器设计及管柱力学分析[D]. 青岛: 中国石油大学(华东), 2011.
[16] 孙爱军, 徐英娜, 李洪洌, 等. 注水管柱的受力分析及理论计算[J]. 钻采工艺, 2003, 26 (3) : 55 –57.
Sun Aijun, Xu Yingna, Li Honglie, et al. Force analysis and theoretical calculation of injection string[J]. Drilling & Production Technology, 2003, 26 (3) : 55 –57.
[17] 马学勇, 李军亮. 注水管柱不同过程受力分析[J]. 石油天然气学报, 2006, 28 (4) : 373 –375.
[18] 许志倩, 闫相祯, 杨秀娟. 深井分层注水管柱受力变形计算方法改进[J]. 油气田地面工程, 2010, 29 (3) : 22 –24.
[19] 唐海雄, 张俊斌, 汪顺文, 等. 高温致测试管柱伸长和受力计算分析[J]. 石油机械, 2010 (5) : 84 –86.
[20] 王隆慧, 李洪春, 刘汝福, 等. 高压注水井套管保护管柱受力分析探讨[J]. 石油矿场机械, 2004, 33 (Z1) : 39 –41.
Wang Longhui, Li Hongchun, Liu Rufu, et al. Analysis and discuss on the force applied on protecting pipe for well casing under high pressure[J]. Oil Field Equipment, 2004, 33 (Z1) : 39 –41.