2. 四川大学水利水电学院水力学与山区河流开发保护国家重点实验室, 四川 成都 610207
2. State Key Laboratory of Hydraulics and Mountain River Engineering, College of Hydraulic and Hydra-electric Engineering, Sichuan University, Chengdu, Sichuan 610207, China
水平管气液两相分层流是石油天然气输送工程和化工工程中最常见的两相流流型之一[1],其特点是除了气液两相与管壁间存在相互摩擦外,由于密度差,第一相(气相)流速明显大于第二相(液相),还存在着气液界面相互作用[2]。目前对气壁剪切和液壁剪切的预测已取得较好的结果[2-4],但对界面剪切应力的预测尚没有一致定论,也是这一领域的重点和难点[5-7]。
目前已建立的机理模型通常是通过构建分层流封闭模型或互补的局部模型,预测分层流流动的压降、持液率和剪切作用等[3, 7]。不同模型的区别主要体现在对界面波和界面形状不同的处理方法[8-10]。例如Taitel Y和Dukler A E[5-6]建立的一维两流体模型假设界面为一水平光滑壁面,其摩擦因子等于气壁摩擦因子。这种假设在湍流较强的流动中预测效果并不理想,为此,一些研究者区分了光滑界面和波动界面[11-13],并分析了界面波对气液界面摩擦因子本构关系的影响[11];还有一些学者将气液界面处理为圆弧凹面[3],或者将气液界面处理为水平粗糙壁面[1, 14],建立了不同的分层流模型。在前人工作基础上,Sidi-Ali K和Gatignol R[15] 建立了将气液界面定义为一个无滑移的水平移动壁面的CFD模型,本文称之为移动壁面模型,并由移动壁面摩擦速度得到气液界面剪切应力,从而改进了Taitel Y和Dukler A E模型。然而该模型预测值仍然明显小于实验间接测量值,这是由于移动壁面模型假设的界面速度为液速平均值,远小于实际的界面速度,同时,这类模型的界面性质并不能引起足够的湍能损失。
本文主要目的是利用FLUENT软件建立基于气相流动的CFD模型,并尝试将气液界面处理为一个固定的、具有均匀剪切应力的水平滑移壁面,称之为剪切滑移壁面模型,以提高对气液界面剪切应力的预测。由于可以直接考虑壁面性质对气相流场分布的影响,使得预测方法更为简单有效。
1 模型建立依据Taitel Y和Dukler A E的两流体模型[5-6],将气液两相单独讨论,分别对气液两相建立动量方程
| $ - A_{\rm{G}} \left( {\dfrac{{{\rm{d}}p}}{{{\rm{d}}z}}} \right) - \tau _{{\rm{WG}}} S_{\rm{G}} - \tau _{\rm{I}} S_{\rm{I}} + {\rm{g}}\rho _{\rm{G}} A_{\rm{G}} \sin \delta = 0 $ | (1) |
| $ - A_{\rm{L}} \left( {\dfrac{{{\rm{d}}p}}{{{\rm{d}}z}}} \right) - \tau _{{\rm{WL}}} S_{\rm{L}} + \tau _{\rm{I}} S_{\rm{I}} + {\rm{g}}\rho _{\rm{L}} A_{\rm{L}} \sin \delta = 0 $ | (2) |
式中:
g-重力加速度,g=9.8 m/s2;
dp/dz-轴向压降,Pa/m。
 |
| 图1 气液两相分层流 Fig. 1 Stratified gas-liquid two-phase flow |
式(1)反映了气相在一封闭固壁管内流动情形。
| $ \tau _{\rm{I}} = \dfrac{D}{4}\left( {\dfrac{{2h_{\rm{L}} }}{D} - 1} \right)\left( {\dfrac{{{\rm{d}}p}}{{{\rm{d}}z}}} \right) - \dfrac{{\cos ^{ - 1} \left( {2h_{\rm{L}} /D - 1} \right)}}{{\sqrt {1 - \left( {2h_{\rm{L}} /D - 1} \right)^2 } }}\left[{\dfrac{D}{4}\left( {\dfrac{{{\rm{d}}p}}{{{\rm{d}}z}}} \right) + \tau _{{\rm{WG}}} } \right] $ | (3) |
式中:D-圆管直径,m;
可见只有准确预测压降和气壁剪切应力才能更好地预测界面剪切应力。由于CFD预测
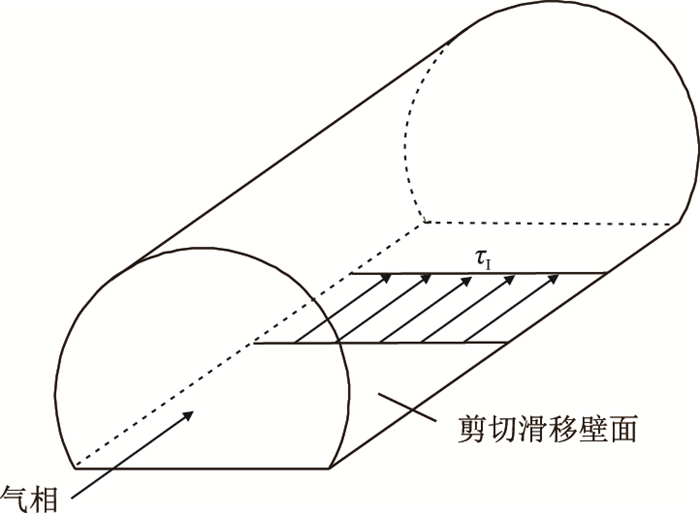 |
| 图2 剪切滑移壁面模型 Fig. 2 Slip-shear-wall model |
实际的气液界面剪切应力分布并不均匀,靠近管壁的剪切应力小,界面中心线位置最大[3-4, 14, 17-18]。剪切滑移壁面模型假设剪切均匀分布,在气液两相的壁面交界处的不连续性很强,这一特征与实际流动非常相似[4]。此外,移动壁面模型的均匀界面速度分布与实际两相界面速度分布也不相同[18],两种类比模型对界面的均匀简化处理的目的之一是为了使用简单边界条件来获得气速的收敛解,同时,简化条件对气相主流区气速分布影响并不大[4, 14-15],这是本文模拟方法的主要依据和条件。
2 模型方程 2.1 控制方程建立气相连续性方程和动量方程
| $ \dfrac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho U_{\rm{i}}} \right) = 0 $ | (4) |
| $ \dfrac{\partial }{{\partial t}}\left( {\rho U_{\rm{i}}} \right) + \nabla \cdot \left( {\rho U_{\rm{ij}}} \right) = - \nabla p + \rho {\rm{g}}_{\rm{i}} + \\ \hspace{2em}\nabla \cdot \left\{ {\mu \left[{\nabla U_{\rm{i}} + \left( {\nabla U_{\rm{i}}} \right)^T } \right]} \right\} $ | (5) |
式中:
t-时间,s;
使用
| $ \dfrac{\partial }{{\partial t}}\left( {\rho k} \right) + \dfrac{\partial }{{\partial x_{\rm{i}} }}\left( {\rho kU_{\rm{i}} } \right) = \dfrac{\partial }{{\partial x_{\rm{j}} }}\left[{\left( {\mu + \dfrac{{\mu _{\rm{t}} }}{{\sigma _{\rm{k}} }}} \right)\dfrac{{\partial k}}{{\partial x_{\rm{j}}}}}\right] +\\ \hspace{3em} \rho P_{\rm{k}} - \rho \varepsilon $ | (6) |
| $ \dfrac{\partial }{{\partial t}}\left( {\rho \varepsilon } \right) + \dfrac{\partial }{{\partial x_{\rm{i}}}}\left( {\rho \varepsilon U_{\rm{i}} } \right) = \dfrac{\partial }{{\partial x_{\rm{j}} }}\left[{\left( {\mu + \dfrac{{\mu _{\rm{t}} }}{{\sigma _\varepsilon}}} \right)\dfrac{{\partial \varepsilon }}{{\partial x_{\rm{j}}}}} \right] +\\ \hspace{3em} C_{1\varepsilon } \rho P_{\rm{k}} \dfrac{\varepsilon}{k} - C_{2\varepsilon } \rho \dfrac{{\varepsilon ^2 }}{k} $ | (7) |
式中:$\mu _{\rm{t}}$-湍动黏度,Pa·s,$\mathop \mu \nolimits_{\rm{t}} = \rho \mathop C\nolimits_{\rm{\mu }} \mathop k\nolimits^2 /\varepsilon$;
经验常量:
对于稳态问题,上述各方程非稳态项为零。
2.2 边界条件入口为平均速度入口
| $ U = U_0 $ | (8) |
式中:
出口边界条件选择压力出口,各量在出口法向n的扩散率为零
| $ \dfrac{\partial }{{\partial n}}\left( {U, k, \varepsilon } \right) = 0 $ | (9) |
管壁处,速度满足无滑移条件
| $ U = 0 $ | (10) |
滑移壁面处,FLUENT在边界上计算切向速度,滑移壁面不使用壁函数,同时,给出壁面剪切应力边界条件
| $ \tau _{\rm{I}} = \tau _0 $ | (11) |
式中:
无滑移管壁面使用低雷诺数两层湍流边界层模型,即黏性支层和对数律层[19-20],则
| $ {U_\tau } = \sqrt {{\tau _{\rm{I}}}/\rho } = C_\mu ^{1{\rm{ /}}4}{k^{1{\rm{ /}}2}} $ | (12) |
| $ U^ + = \dfrac{U}{{U_\tau }} = \left\{ {\begin{array}{*{20}c} {\dfrac{{\rho U_\tau }}{\mu }l = l^ +, \quad l^ + \leqslant 11.225} \\ {\dfrac{1}{\kappa }\ln \left( {El^ + } \right)\, , \quad l^ + > 11.225} \\ \end{array}} \right. $ | (13) |
式中:
l-点到壁面距离,m;
上标:
+-壁面无因次参数,黏性支层的无因次厚度为11.225[19-20]。
3 模拟方法Strand Ø[21]在长35.0 m、直径0.1 m的水平圆管中进行了空气-水两相分层流系统实验,液相表观速度为0.1 m/s。利用FLUENT对前7组(R1~R7)进行模拟。管长10.0 m,直径0.1 m,仅模拟气相流动,考虑重力项(y方向-9.81 m/s2)。管壁内表面建立第一层0.000 1 m、增长率1.2的4层边界层;对于滑移壁面,考虑到较大的速度梯度,对网格进行了相应的细化,见图 3。
 |
|
图3
模型网格划分( |
模拟的基本过程是通过动量方程更新初值气速和剪切应力,经过压力修正使更新值满足连续方程,在湍流方程的控制下,流场和源项得到更新,将模拟得到的流场与实验观测数据(气相流动分布)进行对比,然后进一步更新初值,重复这个过程,直到模拟流场与实验流场吻合得最好。对于速度分布特征的对比,选择管道轴向5 m处(z=5 m,认为流动已充分发展)的两条线速度分布进行对比:中心垂线速度(z=5 m,x=0)和高0.065 m的水平线速度(z=5 m,y=0.065 m)。为做统一对比,引入无因次高度Y和无因次宽度X
| $ Y = \dfrac{{y - h_{\rm{L}} }}{{D - h_{\rm{L}} }}, \;X = \dfrac{{x + x_{\rm{0}} }}{{2x_{\rm{0}} }} $ | (14) |
式中:
图 4和图 5对比了Strand Ø的实验、Sidi-Ali K和Gatignol R与本文的剪切滑移壁面模型得到的速度剖面分布图。图 4为垂线速度分布图;图 5为水平线速度分布图,流场关于x=0近似对称,故仅比较0.5≤X≤1.0的速度,实验R6组测量数据有明显误差[15, 21],不做对比。
 |
| 图4 垂线速度对比(z=5 m,x=0) Fig. 4 Comparisons of vertical velocities (z=5 m, x=0) |
 |
| 图5 水平线速度对比(z=5 m,y=0.065 m) Fig. 5 Comparisons of horizontal velocities (z=5 m, y=0.065 m) |
除R6组外,剪切滑移壁面模型模拟的
表 1给出了实验值以及移动壁面模型和剪切滑移壁面模型的气相速度及剪切应力的模拟结果。其中,移动壁面模型通过摩擦速度求得
| 表1 模拟得到的气相速度、气壁剪切应力和界面剪切应力 Table 1 Simulation values of gas velocities, gas-wall shear stresses and interfacial shear stresses |
剪切滑移壁面模型的滑移壁面滑移速度分布不均匀,利用动量方程预测液相速度
剪切应力和摩擦因子通常使用下式建立计算关系[5-6, 13]
| $ \tau _{{\rm{WG}}} = f_{\rm{WG}} \dfrac{{\rho _{\rm{G}} U_{\rm{G}}^2 }}{2} $ | (15) |
| $ \tau _{\rm{I}} = f_{\rm{I}} \dfrac{{\rho _{\rm{G}} \left( {U_{\rm{G}} - U_{\rm{L}} } \right)^2 }}{2} $ | (16) |
式中:
由于移动壁面模型和剪切滑移壁面模型将气液界面类比为壁面,即只考虑气相固壁单相流动,故使用与式(15)相似的方法计算
| $ \tau _{\rm{I}} = f_{\rm{I}} \dfrac{{\rho _{\rm{G}} U_{\rm{G}}^2 }}{2} $ | (17) |
Taitel Y和Dukler A E认为气液界面与气壁具有相同的摩擦因子[5-6],使用Blasuis公式计算
| $ f_{\rm{I}} = f_{{\rm{WG}}} = 0.046Re_{\rm{G}}^{ - 0.2} $ | (18) |
移动壁面模型得到的
| $ f_{{\rm{WG}}} = 1.14Re_{\rm{G}}^{ - 0.45} $ | (19) |
| $ f_{{\rm{I}}} = 0.94Re_{\rm{G}}^{ - 0.427} $ | (20) |
对于剪切滑移壁面模型,根据模拟收敛结果,计算出气壁和界面摩擦因子,可以拟合得到
| $ f_{{\rm{WG}}} = 0.266Re_{\rm{G}}^{ - 0.317} $ | (21) |
| $ f_{{\rm{I}}} =0.3965Re_{\rm{G}}^{ - 0.336} $ | (22) |
 |
| 图6 剪切滑移壁面模型预测得到的摩擦因子与气相雷诺数的关系 Fig. 6 The relationship between friction factors and gas Reynolds numbers predicted by slip-shear-wall model |
气相雷诺数
| $ Re_{\rm{G}} = \dfrac{{\rho _{\rm{G}} U_{\rm{G}} D_{{\rm{IG}}} }}{{\mu _{\rm{G}} }}, \;D_{{\rm{IG}}} = \dfrac{{4A_{\rm{G}} }}{{S_{\rm{G}} + S_{\rm{I}} }} $ | (23) |
液相雷诺数
| $ Re_{\rm{L}} = \dfrac{{\rho _{\rm{L}} U_{\rm{L}} D_{{\rm{IL}}} }}{{\mu _{\rm{L}} }}, \;D_{{\rm{IL}}} = \dfrac{{4A_{\rm{L}} }}{{S_{\rm{L}} }} $ | (24) |
式(21)和式(22)的适用范围在9 400
使用Strand Ø实验的气速值,维持液高、管径和介质,对比Taitel Y和Dukler A E、移动壁面模型和剪切滑移壁面模型的预测公式计算效果。表 2给出了Taitel Y和Dukler A E(下标“-TD”)、移动壁面模型和剪切滑移壁面模型预测值,预测值分别用
| 表2 使用实验条件[20]预测剪切应力 Table 2 Shear stresses calculated with experimental values |
 |
| 图7 不同模型的界面剪切应力预测值对比 Fig. 7 Predictions of the interface shear stresses by different models |
在9 400
预测效果证明,气相流场的观测在预测气液界面剪切应力时具有重要意义。由于剪切滑移壁面模型的近壁面速度为不均匀的滑移速度,速度的重新分布一方面引起了更大的湍能耗散,另一方面导致模拟得到的气速稍小(见表 1),所以在相同气相雷诺数条件下,剪切滑移壁面模型的界面剪切应力预测值大于移动壁面模型,甚至大于实验值(R1,R3~R5),也正是这个原因,使得剪切滑移壁面模型的整体预测效果更接近实际情况。 但是,提高预测精度的代价是减弱了模型的封闭性。此外,移动壁面模型和剪切滑移壁面模型都是将气液界面类比为水平壁面进行简化计算,因而无法充分考虑界面波或界面形状对摩擦阻力增强的影响[2, 7, 12, 23],特别是当雷诺数较大时,水平壁面模型的预测值必然小于实际值(R6,R7)。
从模拟方法角度分析,移动壁面模型的移动壁面性质取决于界面剪切应力的计算结果,而不是决定界面剪切应力大小;而剪切滑移壁面模型直接考虑了界面性质对气相流场分布的影响,因此方法更为简单有效。
5 结 论(1) 建立了将气液分层流界面处理为具有均匀剪切应力的滑移壁面模型,即剪切滑移壁面模型,利用CFD软件模拟气相流动,得到新的界面摩擦因子表达式(式(22)),对水平管气液两相分层流界面剪切应力进行了预测。
(2) 与Taitel Y和Dukler A E及Sidi-Ali K和Gatignol R的计算模型相比,剪切滑移壁面模型得到的界面剪切应力预测值与Strand的实验间接测量值吻合得最好;但是,水平壁面模型无法考虑界面波与界面形状对界面作用的影响,建议当气相雷诺数(至少)大于50 000时,必须考虑界面形状特性。
(3) 对于模型封闭性,剪切滑移壁面模型需要借助更多的实验经验关系式来封闭模型,如持液率(或液高)和液相平均速度等。
(4) 剪切滑移壁面模型考虑了水平壁面性质对气相流场分布的影响,从而可以直接控制关键参数,为CFD方法预测水平管气液两相分层流界面剪切应力提供了一种简单而可行的思路。
| [1] | 刘夷平. 水平油气两相流流型转换及其相界面特性的研究[D]. 上海:上海交通大学, 2008. |
| [2] | Ullmann A, Brauner N. Closure relations for two-fluid models for two-phase stratified smooth and stratified wavy flows[J]. International Journal of Multiphase Flow, 2006, 32 (1) : 82 –105. DOI:10.1016/j.ijmultiphaseflow.2005.08.005 |
| [3] | Vlachos N A, Paras S V, Karabelas A J. Prediction of holdup, axial pressure gradient and wall shear stress in wavy stratified and stratified/atomization gas/liquid flow[J]. International Journal of Multiphase Flow, 1999, 25 (2) : 365 –376. DOI:10.1016/S0301-9322(98)00049-4 |
| [4] | Mouza A A, Paras S V, Karabelas A J. CFD code application to wavy stratified gas-liquid flow[J]. Chemical Engineering Research & Design, 2001, 79 (5) : 561 –568. |
| [5] | Taitel Y, Dukler A E. A model for predicting flow regime transitions in horizontal and near horizontal gas-liquid flow[J]. AIChE Journal, 2004, 22 (1) : 47 –55. |
| [6] | Taitel Y, Dukler A E. A theoretical approach to the Lockhart-Martinelli correlation for stratified flow[J]. International Journal of Multiphase Flow, 1976, 2 (76) : 591 –595. |
| [7] | Liné A, Lopez D. Two-fluid model of wavy separated twophase flow[J]. International Journal of Multiphase Flow, 1997, 23 (6) : 1131 –1146. DOI:10.1016/S0301-9322(97)00032-3 |
| [8] | Shoham O, Taitel Y. Stratified turbulent-turbulent gasliquid flow in horizontal and inclined pipes[J]. AIChE Journal, 1984, 30 (3) : 337 –385. |
| [9] | Issa R I. Prediction of turbulent,stratified,two-phase flow in inclined pipes and channels[J]. International Journal of Multiphase Flow, 1988, 14 (2) : 141 –154. DOI:10.1016/0301-9322(88)90002-X |
| [10] | Spedding P L, Spence D R. Flow regimes in two-phase gas-liquid flow[J]. International Journal of Multiphase Flow, 1993, 19 (2) : 245 –280. DOI:10.1016/0301-9322(93)90002-C |
| [11] | Kowalski J E. Wall and interfacial shear stress in stratified flow in a horizontal pipe[J]. AIChE Journal, 1987, 33 (2) : 274 –281. DOI:10.1002/(ISSN)1547-5905 |
| [12] | Andritsos N, Hanratty T J. Influence of interfacial waves in stratified gas-liquid flows[J]. AIChE Journal, 1987, 33 (3) : 444 –454. DOI:10.1002/(ISSN)1547-5905 |
| [13] | Tzotzi C, Andritsos N. Interfacial shear stress in wavy stratified gas-liquid flow in horizontal pipes[J]. International Journal of Multiphase Flow, 2013, 54 (3) : 43 –54. |
| [14] | Benkirane R, Liné A, Masbernat L. Numerical modeling of wavy stratified two-phase flow in pipes[J]. Chemical Engineering Science, 2000, 55 (20) : 4681 –4697. DOI:10.1016/S0009-2509(00)00070-1 |
| [15] | Sidi-Ali K, Gatignol R. Interfacial friction factor determination using CFD simulations in a horizontal stratified two-phase flow[J]. Chemical Engineering Science, 2010, 65 (18) : 5160 –5169. DOI:10.1016/j.ces.2010.06.015 |
| [16] | Ghorai S, Nigam K D P. CFD modeling of flow profiles and interfacial phenomena in two-phase flow in pipes[J]. Chemical Engineering and Processing Process Intensification, 2006, 45 (1) : 55 –65. DOI:10.1016/j.cep.2005.05.006 |
| [17] | Newton C H, Behnia M. A numerical model of stratified wavy gas-liquid pipe flow[J]. Chemical Engineering Science, 2001, 56 : 6851 –6861. DOI:10.1016/S0009-2509(01)00322-0 |
| [18] | Ng T S, Lawrence C J, Hewitt G F. Laminar stratified pipe flow[J]. International Journal of Multiphase Flow, 2002, 28 (6) : 963 –996. DOI:10.1016/S0301-9322(02)00004-6 |
| [19] | Launder B E, Sharma B I. Application of the energydissipation of turbulence to calculation of low near a spinning disc[J]. Letters in Heat & Mass Transfer, 1974, 1 (2) : 131 –138. |
| [20] | Launder B E, Spalding D B. The numerical computation of turbulent flows[J]. Computer Methods Applied Mechanics & Engineering, 1974, 3 (2) : 269 –289. |
| [21] | Strand Ø. An experimental investigation of stratified twophase flow in horizontal pipes[D]. Norway:University of Oslo, 1993. |
| [22] | Duan R X, Yu D, Wu H H, et al. Optical method for flow patterns discrimination,slug and pig detection in horizontal gas liquid pipe[J]. Flow Measurement and Instrumentation, 2013, 32 (8) : 96 –102. |
| [23] | Vallée C, Lucas D, Beyer M, et al. Experimental CFD grade data for stratified two-phase flows[J]. Nuclear Engineering & Design, 2010, 240 (9) : 2347 –2356. |
 2015, Vol. 37
2015, Vol. 37


