由于低渗透多孔介质孔隙几何形状的复杂性、流体性质的特殊性和同时受到流动条件的制约,使得流体在低渗透多孔介质中渗流特征不再符合传统的达西渗流规律[1-4],表现为明显的非线性渗流特征,同时具有一定的启动压力梯度。很多学者基于实验和理论研究分析流体性质及流体与多孔介质内表面相互作用机制对低渗透油藏非线性渗流规律的影响。实验研究结果表明低渗透多孔介质固液界面间存在强烈的分子作用力[5]。黄延章[6]认为,吸附在多孔介质内表面的边界流体是导致低渗透油藏流体非线性特征和启动压力梯度存在的主要原因;低渗透油藏尤其是致密低渗透油藏的平均喉道半径与原油边界层在同一个数量级上,必须克服固液界面间的分子作用力才能使边界流体参与流动[7];李兆敏[8]指出,低渗透多孔介质的流体在流动过程中不能保持恒定的特性,表现为Bingham型非牛顿流体特征,即施加的驱动压力梯度大于某个阀值压力梯度后流体才开始流动。在低渗透油藏非线性渗流模型表征方面通过拟合物理实验结果和理论推导建立相应的渗流模型,但其相应的参数在实验室难以获得,物理意义不明确,进而限制了其在油藏工程及数值模拟中的应用。
本文以流体边界层理论为基础,提出一种低渗透油藏流体非线性渗流新模型,在模型推导过程中获得动态启动压力梯度的连续变化函数,并以此模型为基础建立一种分析低渗透油藏动边界变化规律的数值分析方法,与线性渗流模型和拟线性渗流模型下地层压力的变化特征进行了对比;最后,研究了非线性系数对低渗透油藏动边界的扩展特征。
1 低渗透油藏流体非线性渗流模型在低渗透多孔介质中,孔隙半径与流体边界层厚度处于同一个数量级上,流体与多孔介质内表面间的相互作用强烈,影响了流体通过低渗透多孔介质的渗流特征。毛细管实验结果表明[9-10],对于同一根毛细管,驱替压力梯度与流体边界层厚度成反比关系,压力越大,壁面黏滞层越薄,呈现指数衰减的规律。基于上述研究结果,假设流体边界层厚度与驱替压力梯度的变化关系为
| $ \delta = r_0 \cdot \delta _0 \cdot {\rm{e}}^{ - c\left| {\nabla p} \right|} $ | (1) |
式中:
c-流体边界层参数,m·Pa-1;
低渗透油藏,孔隙及喉道半径细小,边界层效应使流体通过喉道时表现为非牛顿Bingham流体的流动特征。对于Bingham流体,当剪切应力
| $ \tau = \tau _0 + \mu _{\rm{B}} \dot \gamma $ | (2) |
式中:
毛细管模型被广泛用来推导多孔介质的渗流模型[13-15],甚至是非牛顿Bingham流体的渗流模型[16-17]。假设一根半径为
| $ \dfrac{{{\rm{d}}\vec v}}{{{\rm{d}}r}} = - \dfrac{1}{{\mu _{\rm{B}} }}\left( {\dfrac{r}{2}\left| {\nabla p} \right| + \tau _0 } \right) $ | (3) |
式中:
r-流体通过毛细管的有效渗流半径,m,
假设边界流体的厚度为
| $ \vec v = - \dfrac{1}{{\mu _{\rm{B}} }}\int_r^{r_0 - \delta } {\left( {\dfrac{r}{2}\left| {\nabla p} \right| + \tau _0 } \right){\rm{d}}r} $ | (4) |
则得到Bingham流体沿半径方向的速度分布
| $ \vec v\!=\!- \dfrac{1}{{\mu _{\rm{B}} }}\left\{ {\left[{\dfrac{{(r_0-\delta )^2\!-\!r^2 }}{4}}\right]\left| {\nabla p} \right|\!+\!\tau _0 \left( {r_0\!-\!\delta\!-\!r} \right)} \right\} $ | (5) |
再对式(5)进行过流断面上的积分,得到单个毛管中的流量公式
| $ q = \int_0^{r_0 - \delta } {\vec v \cdot 2\pi r{\rm{d}}r} = \dfrac{{\pi (r_0 - \delta )^4 }}{{8\mu _{\rm{B}} }}\left| {\nabla p} \right| - \\\hspace{4em}\dfrac{1}{{\mu _{\rm{B}} }}\dfrac{1}{3}\pi \tau _0 (r_0 - \delta )^3 $ | (6) |
式(6)中流体在驱动压力梯度
| $ G = \dfrac{{8\tau _0 }}{{3(r_0 - \delta )}} = \dfrac{{8\tau _0 }}{{3r}} $ | (7) |
式(7)表明:(1)流体通过低渗透多孔介质的启动压力梯度本质上是固-液界面间的屈服应力造成的,数值上与剪切应力大小成正比,与毛细管有效渗流半径成反比;(2)启动压力具有动态特征,随驱替压力梯度的增大,启动压力梯度越小。
特别的,当毛细管中静态边界层厚度为零时,得到毛细管中最小启动压力梯度
| $ G_{\min } = \dfrac{{8\tau _0 }}{{3r_0 }} $ | (8) |
流体通过单个毛细管内的最小启动压力梯度可以应用静态法测量获得[18]。
将式(1)、式(8)代入到式(7)中,得到任意驱替压力梯度下的动态启动压力梯度
| $ G = \dfrac{{G_{\min } }}{{1- \delta _0 \cdot {\rm{e}}^{- c\left| {\nabla p} \right|} }} $ | (9) |
将式(7)代入到式(6)中,得到考虑流体边界层效应的毛管中的流量公式
| $ q = \dfrac{{\pi (1- \delta _0 {\rm{e}}^{ - c\left| {\nabla p - G} \right|} )^4 r_0 ^4 }}{{8\mu _{\rm{B}} }}\left( {1 - \dfrac{G}{{\left| {\nabla p} \right|}}} \right)\nabla p $ | (10) |
式中:
G-流体在驱替压力梯度
q-体积流速,m3/s。
1.2 通过低渗透多孔介质的非线性渗流模型流体通过低渗透多孔介质的渗流模型,可借助毛管束模型推导。将油藏岩芯假设为一组半径为
| $ Q\!=\!\sum\limits_{i\!=\!1}^N {q\left({r_i }\right)}\!=\!\sum\limits_{i\!=\!1}^N {\dfrac{{\pi (1\!-\!\delta_{0i}{\rm{e}}^{\!-\!c_i \left|{\nabla p\!-\!G_i }\right|})^4 r_i ^4 }}{{8\mu_{\rm{B}}}}}\left({1\!-\!\dfrac{{G_i }}{{\left|{\nabla p}\right|}}}\right)\nabla p $ | (11) |
式中:
Q-流量,m3/s;
定义渗流速度
| $ v = \dfrac{Q}{A} = \dfrac{{\sum\limits_{i = 1}^N {q\left( {r_i } \right)} }}{{\left( {\sum\limits_{i = 1}^N {\pi r_i ^2 } } \right)/\phi }} $ | (12) |
得到多孔介质非牛顿Bingham流体渗流模型为
| $ \vec v=\left\{\begin{array}{l} -\dfrac{{K_0 }}{{\mu _{\rm{B}}}}\left[{1\!-\!\delta _{0\phi} {\rm{e}}^{-c_{\phi}\left( {\left| {\nabla p} \right|-G_{\phi}} \right)}}\right]^4 \left({1-\dfrac{G}{{\left|{\nabla p} \right|}}} \right)\nabla p, \left|{\nabla p} \right|>G_{\phi}\\[12pt] 0, \left|{\nabla p}\right|\leqslant G_{\phi} \\ \end{array} \right. $ | (13) |
式中:
A-多孔介质的横截面积,m2;
上式中,当
由上述推导过程可看出,低渗透多孔介质中Bingham流体渗流规律表现为非线性渗流特征,同时又存在动态启动压力梯度;边界层的动态变化是Bingham流体呈现非线性渗流特征的主要原因;低渗透油藏启动压力梯度是流体屈服应力形成的。
公式(13)中
用黏度2 mPa·s的模拟油在某岩芯中进行了压力梯度与流量的关系实验研究,岩芯及流体参数:空气渗透率20 mD,岩芯截面积0.001 m2。应用式(13)对实验结果进行了拟合,所得的结果如图 1所示。拟合得非线性系数
 |
| 图1 Bingham流体通过多孔介质的压力梯度与流量的实验数据拟合 Fig. 1 The experimental data fitting of pressure gradient and flow rate of Bingham fluid through porous media |
图 2表明:随着驱替压力梯度的增大,低渗透多孔介质的启动压力梯度是一个连续变化的过程,当驱替压力梯度增大到一定时,启动压力梯度为常数,此时
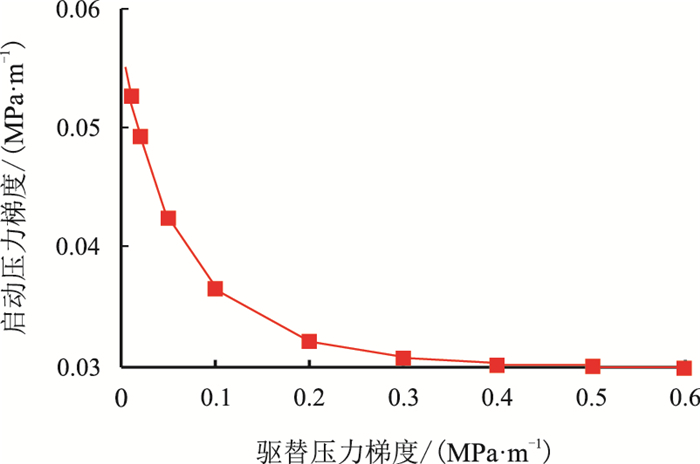 |
| 图2 启动压力梯度与驱替压力梯度的关系曲线 Fig. 2 Kick-off pressure gradient and displacement pressure gradient curve |
对低渗透油藏作如下假设:
(1) 油藏均质且等温;
(2) 流动属于一维水平流动,忽略重力及毛管力的影响;
(3) 流体为非牛顿Bingham流体,其流动方程满足式(13);
(4) 岩石和流体微可压缩,满足以下状态方程
| $ \phi (p) = \phi _0 \left[{1 + c_{\rm{r}} (p-p_0 )} \right] $ | (14) |
式中:
地层中流体的密度是压力的函数,表示为
| $ \rho (p) = \rho _0 {\rm{e}}^{ - \alpha _\rho \left( {p_0 - p} \right)} $ | (15) |
式中:
对于式(13),并根据文献[12],得到Bingham流体的视黏度流变模型为
| $ \left\{ \begin{array}{l} \mu = \mu _{\rm{B}} /\left[{1-\dfrac{G_\phi}{{\left| {\nabla p} \right|}}} \right];\left| {\nabla p} \right| > G_\phi \\ \mu = \infty ;\left| {\nabla p} \right| \leqslant G_\phi \\ \end{array} \right. $ | (16) |
根据上述控制方程(13)、式(14)~式(16),一维低渗透多孔介质不稳定渗流的数学模型可表示为
| $ \dfrac{\partial }{{\partial x}}\left( {\rho v} \right) + q = \dfrac{\partial }{{\partial t}}\left( {\rho \phi } \right) $ | (17) |
初始条件
| $ p(x)|_{t = 0} = p_0 $ | (18) |
内边界条件
| $ q = \dfrac{{2\pi r_{\rm{w}} Kh}}{\mu }\dfrac{{{\rm{d}}p}}{{{\rm{d}}r}}|_{r = r_{\rm{w}} } = p_0 $ | (19) |
式中:
t-时间,s;
K-地层渗透率,D;
h-地层厚度,m;
q-油井地面产量,kg/s。
式(14)~式(19)组成了一维低渗透油藏非稳态渗流数学模型。
3 数值求解上述建立的一维多孔介质流体流动模型中涉及到的流体密度、体积系数、原油黏度、启动压力梯度均为压力的函数,是高度非线性的,需要进行数值求解。在数值求解时需要对方程中的空间传导项、时间累积项和源/汇项进行差分离散。为保证离散后的代数方程组的稳定性,空间传导项采用二阶中心差分近似,时间累积项用一阶向后差分近似。流动方程(17)在节点i的离散格式可写为
| $ \sum\limits_{j = 1}^M {F_{ij}^{n + 1} } + q_i^{n + 1} = \dfrac{{V_i }}{{\Delta t}}\left[{\left( {\rho \phi } \right)^{n + 1}-\left( {\rho \phi } \right)^n } \right] $ | (20) |
式中:
| $ F_{ij} = T_{ij} \cdot \Delta \varPhi _{ij} $ | (21) |
式中:
| $ T_{ij} = \dfrac{{K_i \rho _i }}{{\mu _{{\rm{B, }}i} }}\left( {\dfrac{A}{d}} \right)_{ij} \left( {1 - \delta _{0\phi} {\rm{e}}^{ - c——{\phi}\left| {\dfrac{{ \Delta \varPhi }}{d}} \right|_{ij} } } \right)^4 $ | (22) |
式中:
| $ \Delta \varPhi _{ij} = (\varPhi _j - \varPhi _i )_{ij} = \Delta p_{ij} - G_{ij} \cdot d_{ij} $ | (23) |
式中:
为保证数值求解的稳定性和精度,应用全隐式方法线性化离散差分方程(20),得到任意控制体网格单元i的残差方程为
| $ r_i^{u, n + 1} {\rm{\!=\!}}\sum\limits_{j \ne i} {F_{ij}^{u, n + 1} }\!+\!q_i^{u, n + 1} \!-\!\dfrac{{V_i }}{{\Delta t}}\left[{\left( {\rho \phi } \right)_i^{u, n + 1}\!-\!\left( {\rho \phi } \right)_i^n } \right] $ | (i) |
应用Newton-Raphson迭代法求解方程(20)。对于一维单相流动,有M个质量守恒方程和1个井方程,有M个压力变量和1个井底流压变量,加上初边值条件,方程(20)封闭可解。对于上述方程,Newton-Raphson迭代格式为
| $ \sum {\dfrac{{\partial r_i^{u, n + 1} }}{{\partial p_i }}\left( {\delta p_i^{u + 1, n + 1} } \right)}\!+\! \dfrac{{\partial r_i^{u, n + 1} }}{{\partial p_{{\rm{wf}}} }}\left( {\delta p_{{\rm{wf}}}^{u + 1, n + 1} } \right) \!=\!- r_i^{u, n + 1} $ | (25) |
每次迭代求解后,其压力变量更新形式为
| $ p_i^{u + 1, n + 1} = p_i^{u, n + 1} + \delta p_i^{u + 1, n + 1} $ | (26) |
式中:
i,j-节点单元编号;
M-节点单元总数;
n-当前时间步;
n+1-下一时间步;
u-迭代步;
应用一维低渗透油藏渗流模型研究非线性渗流参数对地层压力分布特征的影响。所使用的岩石及流体参数为L=100 m,h=10 m,
在边界条件和井底流压相同的条件下采用考虑动态启动压力梯度的非线性渗流、考虑最小启动压力梯度的非线性和线性流动规律分别计算低渗透地层压力变化曲线,如图 3所示。在近井区域,采用线性渗流模型时地层压力下降缓慢;考虑动态启动压力梯度的非线性渗流模型时地层压力下降幅度最大;采用考虑最小启动压力梯度的非线性渗流模型时地层压力介于二者之间。在远井地带(流动边界附近)的一个相同泄油半径处,考虑非线性渗流的地层压力大于拟线性渗流模型和线性渗流情况。出现这种现象的主要原因是启动压力梯度的动态变化特征形成的,在近井区域随着驱替压力的增大,启动压力梯度逐渐减小至最小,而远井区域的驱替压力梯度逐渐减小,降低启动压力梯度的能力减弱,减小了地层压力的下降范围。
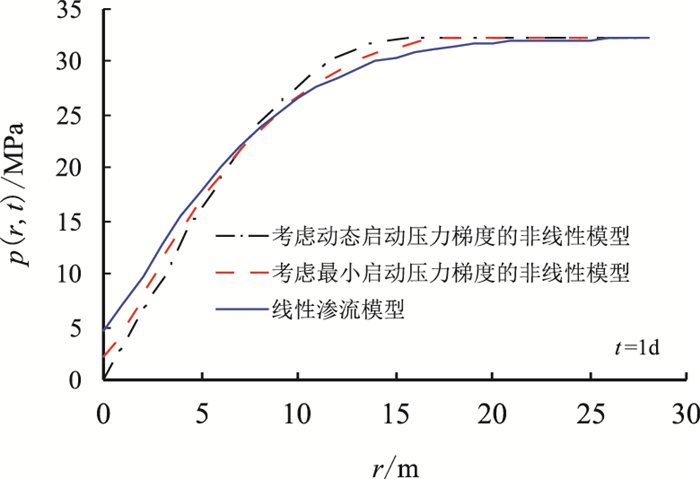 |
| 图3 地层压力分布曲线 Fig. 3 Formation pressure distribution curve |
不同非线性系数下动边界变化曲线如图 4所示。从图 4中可以看出,非线性系数越小,动边界扩展到模型边界需要的时间就越长,任意时刻动边界的距离越小。
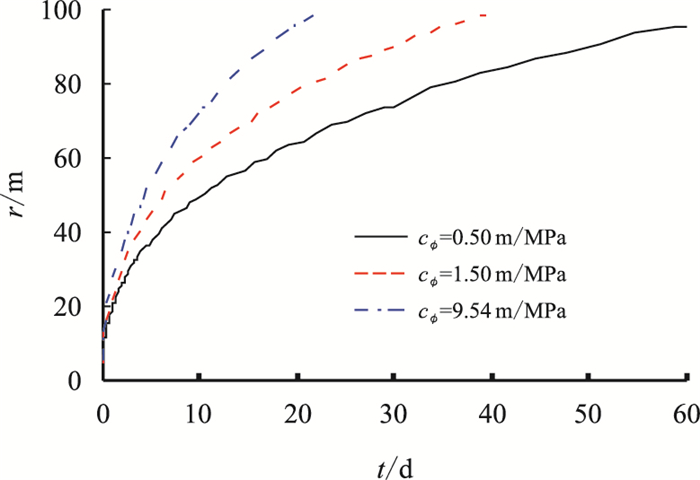 |
| 图4 动边界变化曲线 Fig. 4 Moving boundary curve |
(1) 基于流体边界层理论,提出了一种可用于描述在多孔介质中流动特征非线性渗流模型,获得了动态启动压力梯度的连续变化函数。
(2) 应用考虑动态启动压力梯度的非线性渗流模型,建立了一维单相流体流动的数学模型,并应用全隐式方法对离散方程进行了线性化处理;应用数值方法对比研究了线性渗流模型、拟线性和本文非线性渗流模型下地层压力的分布特征和流体非线性渗流系数对动边界扩展的影响
(3) 数值结果分析表明:与线性渗流和拟线性流动规律相比,反映启动压力梯度的动态变化特征的非线性渗流规律下在近井区域地层压力下降幅度更大,地层压力下降范围小。非线性系数是反映多孔介质渗流阻力大小的综合参数,其数值越小,流体流动的非线性程度越强,动边界的扩展速度越慢。
| [1] | Miller R J, Low P F. Threshold gradient for water flow in clay systems[J]. Soil Science Society of America Proceedings, 1963, 27 (6) : 606 –609. |
| [2] |
冯国庆, 刘启国, 石广志, 等. 考虑启动压力梯度的低渗透气藏不稳定渗流模型[J].
石油勘探与开发, 2008, 35 (4) : 457 –461.
Feng Guoqing, Liu Qiguo, Shi Guangzhi, et al. An unsteady seepage flow model considering kickoff pressure gradient for low-permeability gas reservoirs[J]. Petroleum Exploration and Development, 2008, 35 (4) : 457 –461. DOI:10.1016/S1876-3804(08)60094-4 |
| [3] |
李松泉, 程林松, 李秀生, 等. 特低渗透油藏非线性渗流模型[J].
石油勘探与开发, 2008, 35 (5) : 606 –612.
Li Songquan, Cheng Linsong, Li Xiusheng, et al. Nonlinear seepage flow models of ultra-low permeability reservoirs[J]. Petroleum Exploration and Development, 2008, 35 (5) : 606 –612. DOI:10.1016/S1876-3804(09)60092-6 |
| [4] |
苏海波. 基于边界层理论的低渗透多孔介质非稳态渗流压力变化特征[J].
低渗透油气田, 2015 (1) : 87 –91.
Su Haibo. Characteristics of unsteady-percolation pressure variation in low permeability porous media based on the theory of boundary layer[J]. Low permeability Oil & Gas Fields, 2015 (1) : 87 –91. |
| [5] |
邓英尔, 阎庆来, 马宝岐. 界面分子力作用与渗透率的关系及其对渗流的影响[J].
石油勘探与开发, 1998, 25 (2) : 46 –49.
Deng Ying'er, Yan Qinglai, Ma Baoqi. Relationship between interfacial molecular interaction and permeability and its influence on fluid flow[J]. Petroleum Exploration and Development, 1998, 25 (2) : 46 –49. |
| [6] | 黄延章. 低渗透油层渗流机理[M]. 北京: 石油工业出版社, 1998 . |
| [7] |
李中锋, 何顺利. 低渗透储层非达西渗流机理探讨[J].
特种油气藏, 2005, 12 (2) : 35 –38.
Li Zhongfeng, He Shunli. Non-darcy percolation mechanism in low permeability reservoir[J]. Special Oil and Gas Reservoir, 2005, 12 (2) : 35 –38. |
| [8] | 李兆敏, 蔡国琰. 非牛顿流体力学[M]. 东营: 石油大学出版社, 1998 . |
| [9] |
徐绍良, 岳湘安. 低速非线性流动特性的实验研究[J].
中国石油大学学报:自然科学版, 2007, 31 (5) : 60 –63.
Xu Shaoliang, Yue Xiangan. Experimental research on nonlinear flow characteristics at low velocity[J]. Journal of China University of Petroleum, 2007, 31 (5) : 60 –63. |
| [10] |
徐绍良, 岳湘安, 侯吉瑞, 等. 低边界层流体对低渗透油藏渗流特性的影响[J].
西安石油大学学报:自然科学版, 2007, 22 (2) : 26 –28.
Xu Shaoliang, Yue Xiang'an, Hou Jirui, et al. Influence of boundary-layer fluid on the seepage characteristic of lowpermeability reservoir[J]. Journal of Xi'an Shiyou University:Natural Science Edition, 2007, 22 (2) : 26 –28. |
| [11] | Bird R B, Stewart W E, Lightfoot E N. Transport phenomena[J]. Journal of Applied Mechanics, 1961, 28 (2) : 1274 –1275. |
| [12] | Wu Y S, Pruess K, Witherspoon P A. Flow and displacement of bingham non-newtonian fluids in porous media[C]. SPE 20051, 1992. |
| [13] | 秦积舜, 李爱芬. 油层物理学[M]. 东营: 中国石油大学出版社, 2006 . |
| [14] |
姜瑞忠, 杨仁锋, 马勇新, 等. 低渗透油藏非线性渗流理论及数值模拟方法[J].
水动力学研究与进展:A辑, 2011, 26 (4) : 444 –452.
Jiang Ruizhong, Yang Renfeng, Ma Yongxin, et al. Nonlinear percolation theory and numerical simulation in low permeability reservoirs[J]. Chinese Journal of Hydrodynamics, 2011, 26 (4) : 444 –452. |
| [15] |
时宇, 杨正明, 黄延章. 低渗透储层非线性渗流模型研究[J].
石油学报, 2009, 30 (5) : 731 –734.
Shi Yu, Yang Zhengming, Huang Yanzhang. Study on non-linear seepage flow model for low-permeability reservoir[J]. Acta Petrolei Sinica, 2009, 30 (5) : 731 –734. |
| [16] | 孔祥言. 高等渗流力学[M]. 合肥: 中国科学技术大学出版社, 1999 . |
| [17] | 袁恩熙. 工程流体力学[M]. 北京: 石油工业出版社, 2010 . |
| [18] |
万海艳. 一种微管中启动压力梯度的测量方法[J].
力学与实践, 2013, 35 (6) : 62 –65, 45.
Wan Haiyan. A global-oriented method to measure the threshold pressure gradient in micro-channels[J]. Mechanics in Engineering, 2013, 35 (6) : 62 –65, 45. |
 2015, Vol. 37
2015, Vol. 37


