2. 油气消防四川省重点实验室, 四川 成都 611731;
3. 中国石油西气东输管道公司广东管理处, 广东 广州 510665;
4. 陕西延长石油(集团)管道运输公司, 陕西 延安 716000
2. Oil & Gas Fire Protection Key Laboratory of Sichuan Province, Chengdu, Sichuan 611731, China;
3. Guangdong Regional Office, Petrochina West-east Gas Pipeline Company, Guangzhou, Guangdong 510665, China;
4. Pipeline Company, Yanchang Petroleum Group, Yan'an, Shaanxi 716000, China
随着大量长距离成品油、天然气管道的投产运行,地形起伏管道内积液带来的问题逐渐引起了人们的重视。积液不仅能降低管输效率、加速管道内壁腐蚀,还可在一定条件下引起天然气管道发生冰堵。中国成品油管道已多次发生因管内积水处的腐蚀产物引起输油干线设备的堵塞事故[1]以及清管器卡阻事故,严重影响了管道输油计划的执行以及管道的正常运行。因此,必须采取措施来排除地形起伏管道内的积液。
20世纪60年代开始,有学者对气藏井筒内积液的连续携带规律进行研究[2-9],建立了多种模型用以预测井筒内积液可被携带的临界气速,取得了良好的现场应用效果。然而,由于井筒内积液的力学特性明显区别于地形起伏管道内的积液,其研究成果无法指导地形起伏管道中积液的排除。基于“连续携液”这一思路,作者提出了利用上游来流连续携带管道低洼处积液,其在流动方向上不能满足相对无限长空间内均为两相流体同时存在,称为“局部两相流”。虽与传统两相流存在差异,但仍属于液液两相流范畴,因此可借鉴多相流的研究方法进行研究。
目前多相流研究方法主要有实验环道模拟[10]、半理论半经验理论分析[11, 12]以及数值模拟3种。2011年,徐广丽等[13, 14]提出了水塞模型来描述水平管段局部油水两相流系统水相厚度沿油流流动方向的分布,但此模型假设水平管段下游封堵,不能预测起伏管内积液的界面分布及油流携水的临界参数。2012年,许道振等[15]对积水在5°~30°上倾管道中的运动状况进行了实验分析,发现积水只能在较大油流速度剪切作用下完全被携带出去,然而其研究忽略了水相截面含率变化对界面分布及临界油速的影响。因此,本文采用透明有机玻璃管对起伏管内局部油水两相流系统中积水的分布形态、水相平均截面含率、水相速度等参数进行了实验研究。
1 实验系统采用自行设计的流体环道实验装置[14, 16],如图 1所示,主要包括油相动力与计量系统、测试管段以及水相注入系统,其中透明有机玻璃测试管段管径为50 mm,由水平段、上倾段两段组成,其中上倾管段长4 m,倾角为10°、15°、20°。采用0#柴油、自来水为实验介质,25℃时的密度分别为855.83 kg/m3和977.04 kg/m3,黏度分别为3.430,0.895 mPa·s。
 |
| 图1 油流连续携水实验环道流程图 Fig. 1 Schematic description of the test loop |
柴油存储在储油罐中,由泵打入环道,经标定的流量计进入测试段,最后回到储罐。采用如图 1b所示的注水系统将一定体积的水由注水孔注入水平管段,金属管一端插入水平管段底部,另一端通过密封软管与注射器连接。水相初始截面含率取0.1,0.2,0.3,0.4。
实验开始前,油相在最大流量下流经整个实验环道,以排出环道中的空气。依靠调节阀和旁路系统调节油相流量至所需值后,停泵,利用注射器及图 1b所示注水系统将一定量的水注入水平测试段底部。静置2 min后启泵,采用摄像机拍摄水相的运动形态。实验完毕后,关泵,静置5 min使水回流至水平段,从排水孔将水排出。实验中油相流量范围为0.78~1.91 m3/h。
2 实验结果及讨论 2.1 水相运动形态积水在油流连续剪切作用下,呈现3种分布形态:界面平滑分层流、界面波动分层流、界面乳化分层流,如图 2a~图 2c所示。若管径、上倾倾角、水相初始截面含率不变,油速较小时,积水受到油流剪切较小,积水聚集并停留在弯管处,界面平滑且水相厚度沿油相流动方向呈下游大而上游小的梯度分布,如图 2a所示,这与文献[13]中理论分析的结论一致;随着油速增大,积水进一步聚集至弯管处,下游出现明显的界面波动,并不时有小水团脱离积水主体进入油流,有的小水团团聚为大水团,贴近管壁缓慢回流或向前运动,如图 2b所示;油速继续增大,若剪切力足以克服壁面摩擦力、界面张力及重力,积水会全部进入上倾管段,积水界面波动并缓慢向前爬行,若油速再增大,界面波动加剧至一定程度后不时有小水滴脱离积水主体,并以大于积水主体的速度向前运动,同时界面处形成乳状液,如图 2c所示。
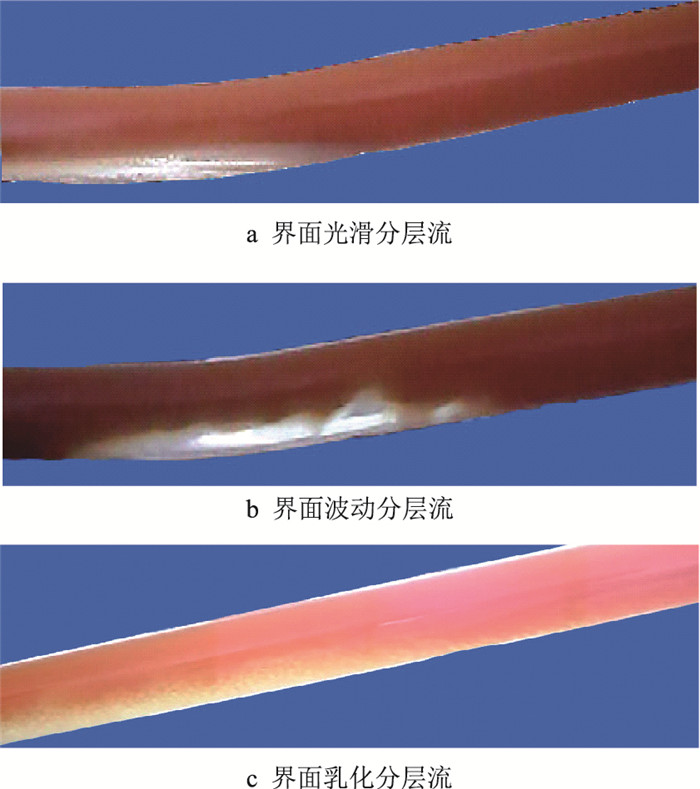 |
| 图2 油流剪切作用下管中积水的分布形态 Fig. 2 The distribution of water sheared by flowing oil |
不同实验工况时的积水分布形态如图 3所示,图中虚线为油相层流-紊流分界线。发现,倾角不变时,初始水相截面含率ε越大,界面产生波动以及界面形成乳状液所对应的油相表观速度均有减小趋势;初始水相截面含率ε不变时,倾角越大,越易有水团脱离积水主体进入油流中,且界面波动随倾角增大而加剧,易于在界面处形成乳状液。
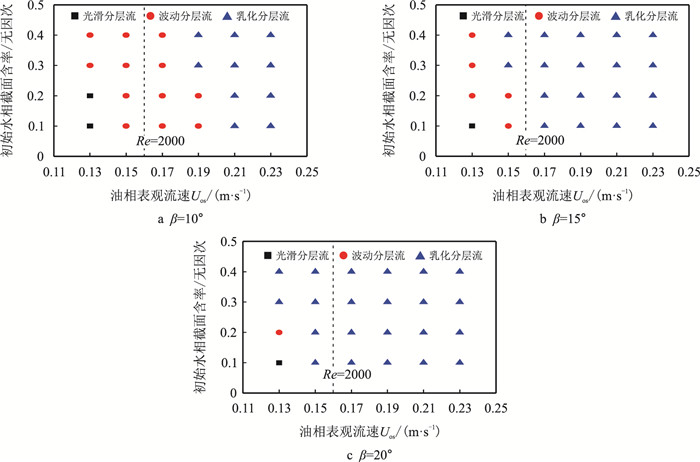 |
| 图3 不同实验工况时的积水分布形态图 Fig. 3 The flow pattern of local oil-water phase flow under different experimental conditions |
观察发现,一旦界面产生波动,部分脱离积水主体的水团会随油流向前运动;若积水全部进入上倾管段,将以一定的速度向前运动。故将此时的油相表观速度分别称为临界表观油速Ⅰ、临界表观油速Ⅱ,记为Uoscr1、Uoscr2。若Uos < Uoscr1,积水聚集在弯管处,不能被油流携带,为界面平滑分层流;若Uoscr1 < Uos < Uoscr2,积水下游波动明显,且有些脱离了积水主体的水团进入油流,为界面波动分层流;若Uos>Uoscr2,积水全部进入上倾管段,除小水团随油流向前运动外,积水主体也以一定速度向前运动,界面波动加剧至一定程度可发生乳化,可为界面波动分层流或界面乳化分层流。这里重点讨论积水可全部携带出去的临界表观油速Ⅱ。
图 4为不同实验工况时的临界表观油速Ⅱ。发现,Uoscr2随上倾倾角的增大而增大、随水相截面含率的变化较小。这说明地形起伏管道中油流连续携带积水的临界条件受上倾管段倾角的影响较大,而受积水量的影响较小。
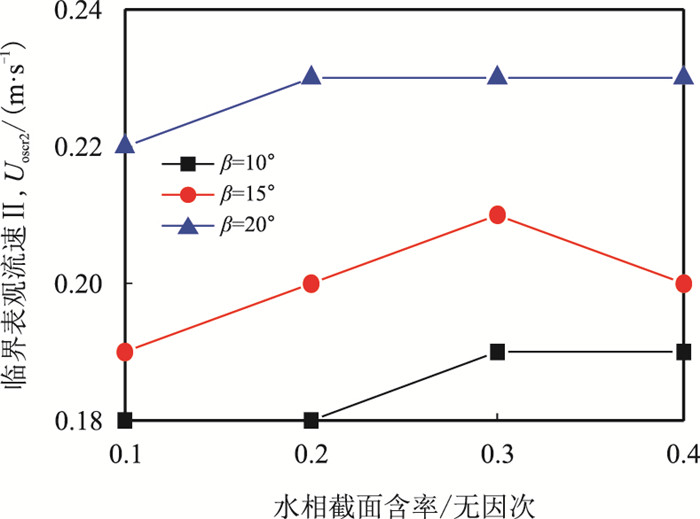 |
| 图4 不同实验工况时的临界表观油速Ⅱ Fig. 4 The critical superficial oil velocity Ⅱ under different experimental conditions |
若Uos>Uoscr2,积水全部能被携带,积水的平均运动速度Uw决定了积水在一定时间内的运动距离,若时间足够长且运动无干扰,则积水可被油流携带进入下游。积水进入上倾管段且流动稳定后,测量积水主体最末端一定时间内通过的距离,即为积水的平均运动速度Uw。如图 5为初始水相截面含率0.3时水相平均运动速度Uw随油相表观速度的变化,图中实线为拟合曲线,从上到下关系式分别为Uw=0.54·Uos-0.11、Uw=0.48·Uos-0.10、Uw=0.27·Uos-0.06。发现,Uw随Uos的增大而线性递增,说明积水与油流之间存在速度滑移;上倾倾角越大,其递增速率减小。等量的积水在相同油相剪切作用下的平均运动速度随上倾倾角增大而减小。
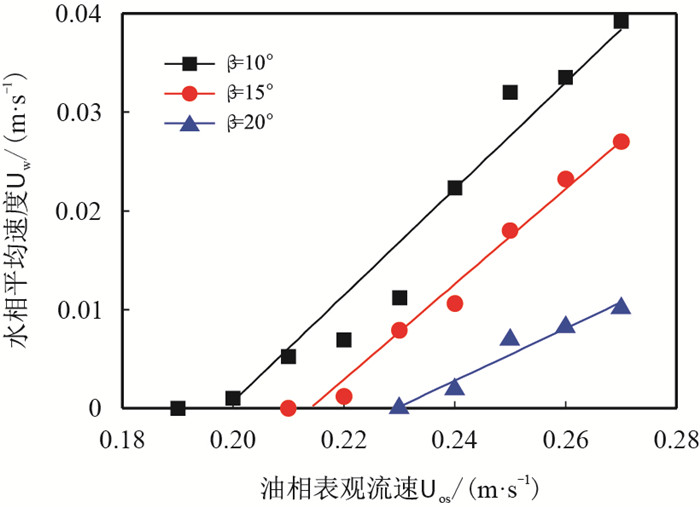 |
| 图5 初始水相截面含率为0.3时,水相平均运动速度随油相表观速度的变化 Fig. 5 Relationship between the average water velocity and the superficial oil velocity when the initial water phase holdup equals 0.3 |
观察发现,积水全部进入上倾管段后,油流剪切作用越大,积水长度越大。若采用Matlab处理测得的水相动态图像,并进行二值化赋值,可得到水相在上倾管段分布的长度L、任意位置处界面至管壁的深度h,按式(1)进行计算,可得到水相的平均截面含率εep。
| $ {\varepsilon _{{\rm{ep}}}} = \frac{{\int_0^L {\left[{{R^2}\arccos \frac{{R-h}}{R}-\left( {R-h} \right)\sqrt {{R^2} - {{\left( {R - h} \right)}^2}} } \right]{\rm{d}}x} }}{{{\rm{\pi }}{R^{\rm{2}}}L}} $ | (1) |
式中:
εep -水相的平均截面含率,无因次;
R-管径,m;
L-水相在上倾管段分布的长度,m;
h-任意位置处界面至管壁的深度,m。
如图 6为初始水相截面含率ε为0.3、上倾倾角β为10°时上倾管内水相平均截面含率εep与油相表观速度Uos的关系,发现εep随Uos的增大而线性递减,其拟合方程为εep=0.31-0.79·Uos。需指出,按式(1)计算εep时,忽略了油水界面曲率,必然存在误差。为验证计算方法的合理性,取材质、内外径均与测试段一致的管段0.5m,装入一定体积比率(0.1~0.5)的实验介质(柴油、自来水),水平放置并拍摄图像,采用上述方法计算平均截面含率,发现误差均小于2%。
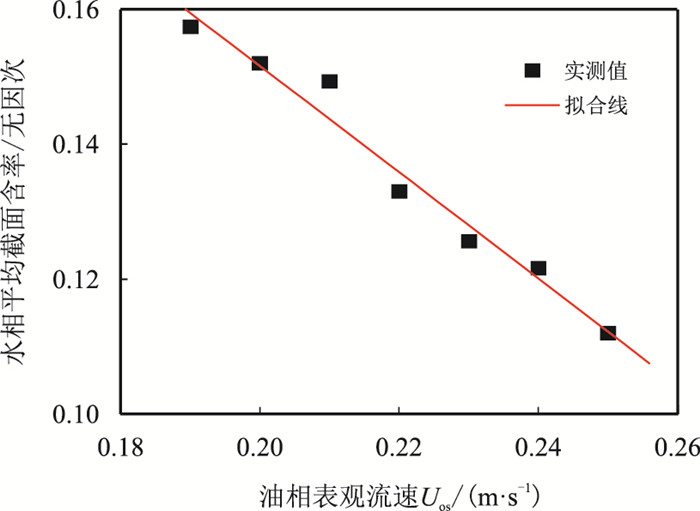 |
| 图6 εep=0.3、β=10°时上倾管内水相平均截面含率与油相表观速度的关系 Fig. 6 Relationship between the average water phase holdup and the superficial oil velocity when the initial phase of void ratio equals 0.3 and the inclination angle equals 10° |
(1)在油流剪切作用下,积水厚度呈下游大上游小的梯度分布;随着油速增大,下游产生波动,并不时有小水团脱离积水主体向前运动或者发生回流;若波动加剧至一定程度,界面处形成油包水型乳状液。
(2)积水全部进入上倾管段时对应的油相表观速度称为临界表观油速Ⅱ,它随上倾倾角增大而增大,受积水量的影响较小。
(3)若积水全部进入上倾管段,积水平均运动速度Uw与Uos存在速度滑移,Uw随Uos增大而线性递增,平均截面含率Uos随Uos增大而线性递减。
(4)利用上游来流携带低洼处积水的思路是可行的。
| [1] |
宋飞, 朱峰, 潘红梅, 等. 兰成渝管道杂质来源分析[J].
油气储运, 2010, 29 (5) : 381 –383.
Song Fei, Zhu Feng, Pan Hongmei, et al. Analysis on impurity origin of Lanzhou-Chengdu-Chongqing Oil product pipeline[J]. Oil & Gas Storage and Transportation, 2010, 29 (5) : 381 –383. |
| [2] | Turner R G, Hunnard M G, Dukler A E. Analysis and prediction of minimum flow rate for the continious removal of liquids from gas wells[C]. SPE 2198, 1968. |
| [3] | Coleman S B, Clay H B, McCurdy D G, et al. A new look at prediction gas-well load-up[J]. Journal of Petroleum Technology, 1991, 43 (3) : 329 –333. DOI:10.2118/20280-PA |
| [4] | 杨川东. 采气工程[M]. 北京: 石油工业出版社, 2000 . |
| [5] |
李闽, 孙雷, 李士伦. 一个新的气井连续排液模型[J].
天然气工业, 2001, 21 (5) : 61 –63.
Li Min, Sun Lei, Li Shilun. A new gas well liquid continuous withdrawal model[J]. Natural Gas Industry, 2001, 21 (5) : 61 –63. |
| [6] |
肖高棉, 李颖川, 喻欣. 气藏水平井连续携液理论与实验[J].
西南石油大学学报:自然科学版, 2010, 32 (3) : 122 –126.
Xiao Gaomian, Li Yingchuan, Yu Xin. Theory and experiment research on the liquid continuous removal of horizontal gas well[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2010, 32 (3) : 122 –126. |
| [7] |
高武彬, 李闽, 洪舒娜, 等. 用白庙气田气井资料对携液模型进行对比分析[J].
新疆石油地质, 2009, 30 (3) : 366 –368.
Gao Wubin, Li Min, Hong Shuna, et al. Analysis and comparison of liquid loading models with gas well information in Baimiao Gas Field[J]. Xinjiang Petroleum Geology, 2009, 30 (3) : 366 –368. |
| [8] |
魏纳, 孟英峰, 李悦钦, 等. 井筒连续携液规律研究[J].
钻采工艺, 2008, 31 (6) : 88 –90.
Wei Na, Meng Yingfeng, Li Yueqin, et al. Research on liquids continuous removal laws in gaswell[J]. Drilling & Production Technology, 2008, 31 (6) : 88 –90. |
| [9] |
王志彬, 李颖川. 气井连续携液机理[J].
石油学报, 2012, 33 (4) : 681 –686.
Wang Zhibin, Li Yingchuan. The mechanism of continuously removing liquids from gas wells[J]. Acta Petrolei Sinica, 2012, 33 (4) : 681 –686. |
| [10] |
肖荣鸽, 魏炳乾, 沙海涛, 等. 气液两相段塞流的PSD和PDF特征分析[J].
西安石油大学学报:自然科学版, 2012, 27 (5) : 58 –62.
Xiao Rongge, Wei Bingqian, Sha Haitao, et al. Analysis of the PSD and PDF characteristics of gas-liquid slug flow[J]. Journal of Xi'an Shiyou University:Natural Science Edition, 2012, 27 (5) : 58 –62. |
| [11] | 徐广丽.成品油管道油携水机理研究[D].青岛:中国石油大学(华东), 2011. http://cdmd.cnki.com.cn/article/cdmd-10425-1011286419.htm |
| [12] | 肖荣鸽, 王立洋, 邓志安, 等. 凝析天然气管道分层流动相间水利摩阻系数计算式评价[J]. 西安石油大学学报:自然科学版, 2006, 21 (3) : 55 –57. |
| [13] |
徐广丽, 张国忠, 赵仕浩, 等. 水平管内油流携水系统特性分析[J].
西南石油大学学报:自然科学版, 2011, 33 (3) : 173 –177.
Xu Guangli, Zhang Guozhong, Zhao Shihao, et al. Analysis of characteristics of the oil purging water systerm in horizontal tube[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2011, 33 (3) : 173 –177. |
| [14] | Xu Guangli, Zhang Guozhong, Liu Gang, et al. Trapped water displacement from low section of oil pipelines[J]. International Journal of Multiphase Flow, 2011, 37 (1) : 1 –11. DOI:10.1016/j.ijmultiphaseflow.2010.09.003 |
| [15] |
许道振, 张国忠, SrdjanN, 等. 积水在上倾输油管中运动状态研究[J].
中国石油大学学报:自然科学版, 2012, 36 (6) : 147 –152.
Xu Daozhen, Zhang Guozhong, Srdjan N, et al. Study on movement of residual water in upward inclined pipeline[J]. Journal of China University of Petroleum, 2012, 36 (6) : 147 –152. |
| [16] |
徐广丽, 张国忠, 赵仕浩. 管道低洼处积水排除实验[J].
油气储运, 2011, 30 (5) : 369 –372.
Xu Guangli, Zhang Guozhong, Zhao Shihao. An experiment on dewatering for lower location of pipeline[J]. Oil & Gas Storage and Transportation, 2011, 30 (5) : 369 –372. |
 2015, Vol. 37
2015, Vol. 37


