2. 中国石油川庆钻探工程有限公司地球物理勘探公司, 四川 成都 610213;
3. 中国石油物探技术试验基地山地地震技术试验基地, 四川 成都 610213;
4. 新疆阜康准东石油基地勘探开发研究所, 新疆 阜康 831511;
5. 中国石油新疆油田分公司陆梁油田作业区, 新疆 克拉玛依 834000
2. Geophysics Prospecting Company, CCDC, CNPC, Chengdu, Sichuan 610213, China;
3. Mountain Geophysical Technology Test Center, CNPC, Chengdu, Sichuan 610213, China;
4. Exploration and Development Research Institute, Xinjiang Fukang Zhundong Oil Base, Fukang, Xinjiang 831511, China;
5. Luliang Oilfield Operation District, Xinjiang Oilfieled Company, CNPC, Karamay, Xinjiang 834000, China
反褶积技术是目前提高地震数据分辨率最主要的方法,常规反褶积方法对褶积模型基于地震子波是最小相位子波的假设[1],使得常规反褶积可以得到反射系数在最下二乘意义下的解,并以此来近似实际地层反射系数。
但是,无数勘探实践证明:实际地震勘探的子波绝大多数为混合相位子波,常规反褶积方法对地震子波所要求的最小相位假设与地震勘探实践相矛盾,容易引发“剩余相位”的解释陷阱,这在很大程度上降低了常规反褶积方法提高地震勘探分辨率的能力。
如果能够从地震记录中估算出混合相位子波[2],那么褶积模型中只有反射系数是未知的,就能够利用维纳滤波方法由褶积模型计算反射系数,从而达到提高地震资料分辨率的目的。因此,从地震记录中估计混合相位子波成为提高地震资料分辨率的关键。
Lazear G D[3]提出利用高阶累积量估计混合相位子波,但该方法不仅算法复杂,其对随机噪声的敏感性也很难满足实际地震资料处理的要求。Porsani M J和Ursin B[4-5]给出了一种解两次YW方程来获取混合相位子波的思路,但该方法多次求解YW方程,使得求解的累计误差严重影响了混合相位子波的估算精度和对实际地震资料的适应性。
由于地层的吸收作用,实际地震信号中的高频成分较弱,很容易受到高频噪声的污染。地震记录经过常规反褶积处理之后,在增强高频信号的同时,高频噪声也被相应地放大。反褶积在提高分辨率的同时,降低了地震记录的信噪比,信噪比与分辨率的矛盾在实际地震勘探工作中十分突出。
Widess M B[6]在分辨率的定义中引入了噪声的影响,并提出了信号纯度的概念。李庆忠[7-8]在对信噪比与分辨率的矛盾深入研究之后指出:反褶积虽然降低了地震记录信噪比,但并不改变地震记录信噪比谱。Puryear C I和Castagna J P[9]利用谱反演,Velis D R[10]利用随机稀疏脉冲反褶积较大幅度地提高了地震记录的分辨率,但没有涉及噪声对反褶积的影响。
由于高频噪声的影响,实际地震记录在提高分辨率的同时,降低了地震资料的信噪比,信噪比和分辨率的矛盾在实际地震勘探中十分突出。如何在提分辨率的同时,较好地保持地震记录的信噪比,达到分辨率和信噪比的相对和谐,是勘探地球物理工作者普遍关心的问题。
本文在前人研究的基础上[11-15],提出一种基于相位分解并能保持信噪比的混合相位子波反褶积方法,实现混合相位子波反褶积,在提高地震记录分辨率的同时,能自动控制高频噪声放大效应对地震记录信噪比的影响,达到信噪比和分辨率的相对和谐,提高地震记录的整体质量,增强地震记录表征地下构造的能力。
1 保持信噪比的混合相位反褶积原理混合相位子波反褶积的关键是如何从地震记录中提取混合相位子波。混合相位子波由振幅谱和相位谱两部分构成,其中振幅谱的估算比较稳定,但要在保持信噪比下估算期望振幅谱则是个难点;而另一个难点则是如何确定混合相位子波的相位谱,因为相位谱对误差比较敏感,现有的相位谱估算方法很难适应实际地震记录的复杂性。
当确定了希望输出振幅谱的零相位子波与实际输入混合相位子波进行匹配滤波后,得到高分辨率反褶积滤波器,最后进行混合相位子波反褶积得到高分辨处理结果,具体工作流程如图 1所示。
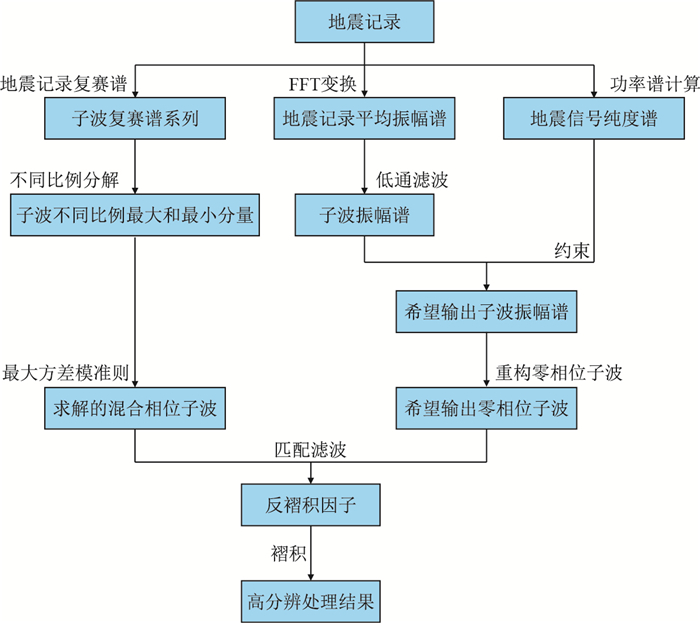 |
| 图1 保持信噪比的相位分解反褶积处理基本流程 Fig. 1 The basic process of keeping the SNR and phase decomposition in deconvolution |
混合相位子波由最大相位分量和最小相位分量两部分构成,而这两个分量的不同分解比例决定了地震子波的相位特征。在所有的分解比例中,存在这样一种分解比例,利用该比例得到的混合相位子波使得反褶积之后地震记录的方差模最大,则该混合相位子波就是实际地震记录的子波[16-18]。
忽略噪声项,地震记录在频率域表达为
| $ x(\omega ) = w(\omega )\xi (\omega ) $ | (1) |
式中:
x(ω),w(ω),ξ(ω)——地震记录、子波和反射系数的频率域表达式,ω——频率,Hz。
对式(1)取对数,有
| $ \ln x(\omega ) = \ln w(\omega ) + \ln \xi (\omega ) $ | (2) |
对式(2)作傅里叶反变换,有
| $ \tilde x(t) = \tilde w(t) + \tilde \zeta (t) $ | (3) |
式中:$\tilde x(t)$,$\tilde w(t)$,$\tilde \zeta (t)$——时间域地震记录(x(t))、子波(w(t))和反射系数($\xi (t)$)的复赛谱序列。
对地震记录复赛谱序列($\tilde x(t)$)进行低通滤之后再进行傅里叶变换,并取幂指数,得到地震子波的振幅谱(w(f))。然后,对振幅谱(w(f))取对数,再进行傅里叶反变换,得到零相位子波的复赛谱序列($\tilde w(t)$),就可对子波的两个分量按比例进行分解。
设定最小分解比例$\lambda _{\min }=0$,最大分解比例$\lambda _{\max }=1.00$,分解比例增量$\Delta\lambda _{\max }=0.01$,分别计算不同分解比例($\lambda _j={\lambda _{\min }} + (j -1)\Delta \lambda$,$j=$1,2,$\cdots$,101)所对应的混合相位子波(${w_j}(t)$)。
按照分解比例($\lambda _j$),根据式(4)和式(5)就可以得到最大相位的复赛谱序列($\tilde{u}_{j}(t)$)和最小相位的复赛谱序列($\tilde{v}_{j}(t)$)
| $ {{\tilde u}_j}\left( t \right) = \left\{ {\begin{array}{*{20}{l}} {{\lambda _i}\tilde w\left( t \right),\;\;t \ge 0}\\ {0,\;\;\;\;\;\;\;\;\;t < 0} \end{array}} \right. $ | (4) |
| $ {{\tilde u}_j}\left( t \right) = \left\{ {\begin{array}{*{20}{l}} {0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t \ge 0}\\ {\tilde w\left( t \right) - {\lambda _i}\tilde w\left( { - t} \right),\;\;t < 0} \end{array}} \right. $ | (5) |
分别对$\tilde{u} (t)$和$\tilde{w} (t)$进行傅里叶变换,并取幂指数,再进行傅里叶反变换,得到分解比例$\lambda _j$所对应的最小相位子波分量($v_j(t)$)和最大相位子波分量($u_j(t)$),对这两个子波分量进行褶积,就能得到分解比例$\lambda _j$所对应的混合相位子波($w_j(t)$),即
| $ w_j(t) = v_j(t)*u_j(t) $ | (6) |
重复上面的操作,就能得到101个具有相同振幅谱、不同相位谱的混合相位子波集合($w_j(t)$,$j=$1,2,$\cdots$,101),那么就能计算每个混合相位子波($w_j(t)$)的反滤波器($\alpha_j(t)$),对反滤波器($\alpha_j(t)$)与地震记录($x(t)$)进行反褶积,得到反褶积之后的地震记录($y_j(t)$)。
计算反褶积之后地震记录的方差模
| $ {e_j} = \dfrac{{\sum\limits_t {y_j^4(i)} }}{{{{\left( {\sum\limits_t {y_j^2(i)} } \right)}^2}}} $ | (7) |
最大方差模所对应的混合相位子波即为实际混合相位地震子波($w_{\rm{mix}}(t)$)。
1.2 信噪比谱约束下提取希望子波振幅谱信噪比是指整个地震记录中信号能量与噪声能量之比,而信噪比谱是指每个频率成分上信号能量与噪声能量之比,两者既有联系、也有区别[19-20]。信号纯度谱是与信噪比谱有关的概念,是指每个频率成分上信号能量与地震数据能量之比。
假设有信号($s(t)$)和噪声($n(t)$)构成的地震记录($x(t)$),则在频率域可表示为
| $ $ | (8) |
则地震记录的信号纯度定义为
| $ \begin{array}{l} P = \frac{{\int {{s^2}} (t){\rm{d}}t}}{{\int {{s^2}} (t){\rm{d}}t + \int {{n^2}} (t){\rm{d}}t}}\\ \;\;\; = \frac{{\int {{S^2}} (f){\rm{d}}f}}{{\int {{S^2}} (f){\rm{d}}f + \int {{N^2}} (f){\rm{d}}f}} = \frac{1}{{1 + 1/R}} \end{array} $ | (9) |
式中:R——信噪比,无因次。
信号纯度谱为每一个频率的信号纯度,为不失一般性,定义
| $ P(f) = \dfrac{{\left| {{S^2}(f)} \right|}}{{\left| {{S^2}(f)} \right| + \left| {{N^2}(f)} \right|}} = \dfrac{1}{1 + 1/R(f)} $ | (10) |
式中:R(f)——信噪比谱。
假设反褶积之后的地震记录在频率域表达式为
| $ $ | (11) |
式中:H(f)——频率反褶积算子。
则反褶积之后的信号纯度谱为
| $ {P_y}(f) = \dfrac{{\left| {H(f)} \right|\left| {S(f)} \right|}}{{\left| {H(f)} \right|\left[{\left| {S(f)} \right| + \left| {N(f)} \right|} \right]}}\\ \;\;\;\;\;\;\;\; = \dfrac{1}{1 + 1/R(f)} = P(f) $ | (12) |
由式(12)可以看出:对于含有高频噪声的地震记录而言,虽然反褶积会降低地震记录的信噪比,但对于给定的频率而言,由于信号和噪声以相同的比例因子放大或减小,反褶积并不改变地震记录的信噪比谱和信号纯度谱。
线性反褶积方法的核心思想是通过展宽地震子波的频谱来压缩子波。这涉及两个主要问题,一是如何从地震记录中估算地震子波的振幅谱,二是如何确定希望输出子波。
关于如何从地震记录中估算地震子波的振幅谱,相关文献较多,谱模拟方法是最为常用的一种方法,但是,对于具有两个以上峰值的地震子波,传统的谱模拟方法会出现较大误差,为此,本文提出了一种基于低通滤波的地震子波振幅谱估算方法。
在不考虑噪声的情况下,希望输出子波的振幅谱越宽,则分辨率越高。但是,由于地层吸收的影响,在地震记录的高频成分中,信号要远远弱于噪声。高频成分被放大之后,虽然提高了地震记录的分辨率,但信噪比会大幅下降。故如何在提高地震记录分辨率的同时,相对保持地震记录的信噪比,是实际地震记录高分辨率处理普遍关心的问题。
反褶积之后地震记录的频谱形态,决定了分辨率和信噪比。因此,需要确定一个兼顾信噪比和分辨率的最佳希望输出频谱,使得反褶积之后地震剖面的整体质量得到最大限度的改善。而信号纯度谱描述了每一个频率成分的信号纯度,且反褶积前后保持不变,将其做为反褶积之后希望输出的频谱,能够取得信噪比和分辨率的相对平衡。
对地震记录(xi(t),i=1,2,$\cdots$,n)做傅里叶变换,得到地震记录的傅里叶变换(Xi(f))和振幅谱(Ai(f)),以第i个地震道为中心,计算2m+1个相邻地震道的平均振幅谱($\bar{a}_i(f)$),再利用下式的低通滤波算子(C(f))与平均振幅谱($\bar{a}_i(f)$)进行褶积运算,得到地震子波的振幅谱(Wi(f)),并绘制在交互面板上,通过样条拟合得到其振幅走势曲线,如图 2所示。
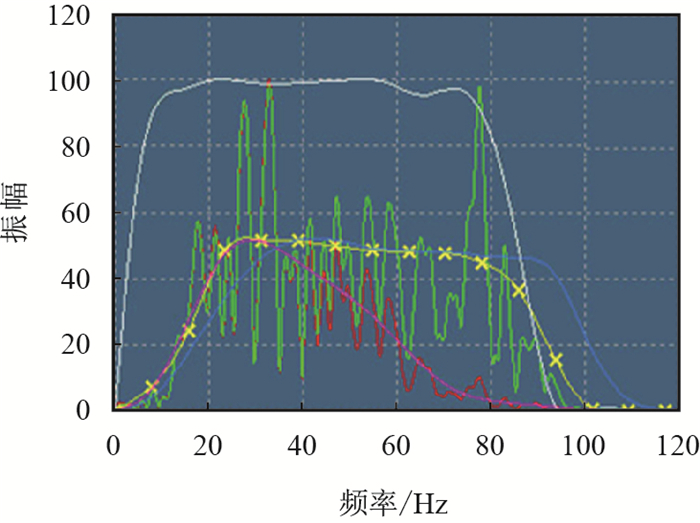 |
| 图2 交互定义希望输出子波振幅谱 Fig. 2 Interactive definition to the output the desired wavelet amplitude spectrum |
| $ C\left( f \right) = \left\{ {\begin{array}{*{20}{l}} {1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;|f| \le \;{f_{\rm{l}}}\;\;\;}\\ {({f_{\rm{l}}} + {f_{\rm{p}}} - |f|)/{f_{\rm{p}}}\;\;\;\;{f_{\rm{l}}} < \;|f| < {f_{\rm{l}}}\; + \;{f_{\rm{p}}}}\\ {1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;|f| \ge {f_{\rm{l}}}\; + \;{f_{\rm{p}}}} \end{array}} \right. $ | (13) |
式中:
fl——高截频率,Hz,取值区间3~7 Hz;fp——斜坡长度,Hz,取值区间3~5 Hz。
目前工业界比较成熟的噪声检测方法都可以扩展为信号纯度谱的估算方法,但一般很难满足工业界地震资料处理稳定高效的要求。为此,选择基于地震信号横向相关性的信号纯度谱估算方法。
以地震记录的傅里叶变换(Xi(f))和振幅谱(Ai(f))计算地震记录的信号纯度谱(Pi(f))。以第i个地震道为中心,计算2m+1个相邻地震道的平均功率谱
| $ {G_i}(f) = \dfrac{1}{{2m + 1}}\sum\limits_{j = - m}^m {A_{i - j}^2(f)} $ | (14) |
则地震信号的平均功率谱为
| $ {U_i}(f) = \dfrac{1}{{2m}}\sum\limits_{j = - m}^{m - 1} {\left [{X_{i + j}}(f){\bar{X}_{i + j + 1}}(j) + {{X}_{i + j + 1}}(j){\bar{X}_{i + j}}(f)\right]} $ |
式中:Xi(f)——第i个地震记录的傅里叶变换。
利用式(14)和式(15),由信号功率谱与地震记录功率谱之比确定信号纯度谱(Pi(f)),并绘制在交互面板上,如图 2中的白色曲线。
| $ {P_i}(f) = \dfrac{{{U_i}(f)}}{{{G_i}(f)}} $ | (16) |
如图 2所示,把信号纯度谱(Pi(f))曲线趋势做为希望输出子波振幅谱($\bar{W}_i(f)$)曲线趋势,通过输入子波振幅谱(Wi(f))曲线拟合恢复得到希望输出子波振幅谱($\bar{W}_i(f)$),从而得到希望输出零相位子波($\bar{W}_i(t)$)。
2 理论模型测试 2.1 混合相位子波提取实验利用模型数据对方法的有效性进行了实验分析,图 3a是混合相位子波,图 3b是反射系数序列,图 3c是混合相位子波与反射系数褶积后的地震记录。图 3d是利用本文方法提取的混合相位子波与实际子波的对比情况,两者的相似系数达到98%,证明该方法是正确有效的。
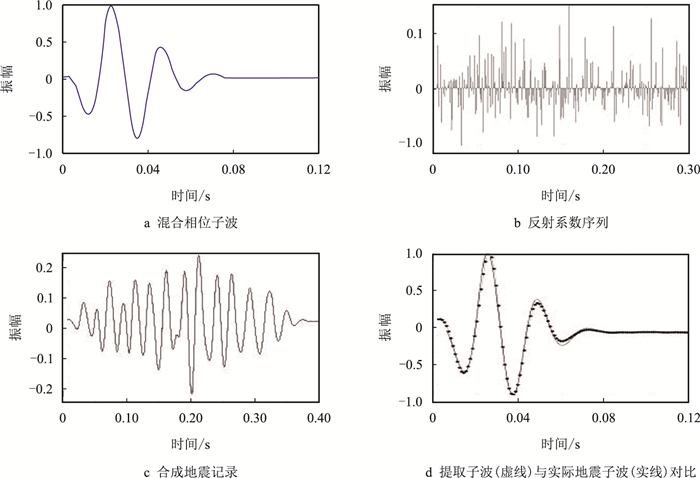 |
| 图3 混合相位子波提取模型实验 Fig. 3 Model experiment of mixed phase wavelet extraction |
利用模型数据对信号纯度谱的估算方法进行了实验分析,图 4a是不含噪声的地震记录,图 4b是加入噪声之后的地震记录,图 4c是利用地震记录的平均功率谱和有效信号的平均功率谱计算得到的实际信号纯度谱,图 4d是利用本文方法估算的信号纯度谱,两者具有较为一致的相似性,证明利用该方法估算信号纯度谱是正确有效的。
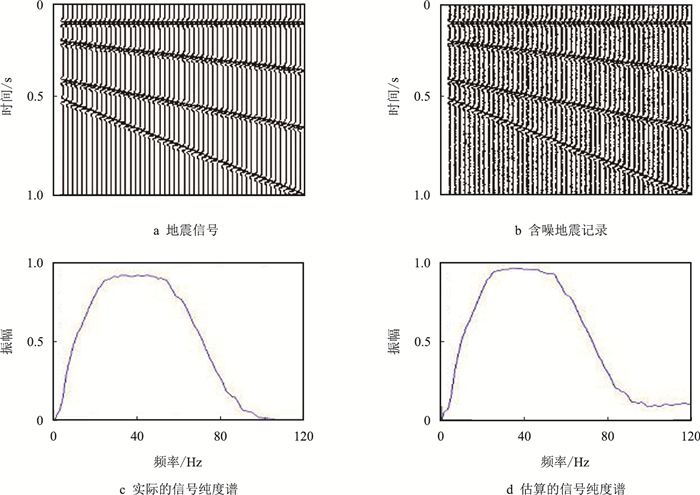 |
| 图4 模型数据信号纯度谱估算实验 Fig. 4 Signal purity spectrum estimation experiment with model data |
为验证上述理论和方法的实际应用效果,选取四川盆地某地区的一段实际资料进行测试。
从图 5提高分辨率前后剖面对比可知:常规反褶积与本文方法都不同程度提高了目的层剖面的分辨率,但本文方法较常规反褶积处理后的剖面分辨率更高,层间信息更加丰富,更好地反映了目的层结构细节,由于常规反褶积没有对信噪比进行有效约束,处理后的剖面较本文方法信噪比低,高频噪音严重,对后续研究地层岩石的性质影响较大。
 |
| 图5 提高分辨率前后剖面对比 Fig. 5 Comparison of the post stack section before and after improving resolution |
从图 6处理前后振幅谱对比分析可知:处理后的频带较处理前有所展宽,但是常规反褶积处理后振幅谱的低频信息有损失,高频能量过强,而本文方法处理后振幅谱低频信息保持较好,振幅谱能量相对均衡。
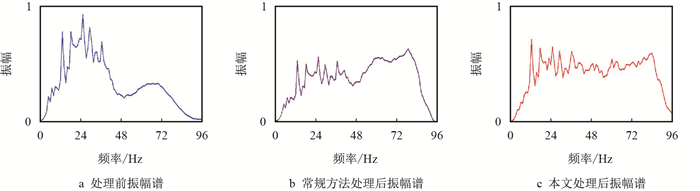 |
| 图6 处理前后振幅谱 Fig. 6 Amplitude spectrum before and after processing |
提出的保持信噪比的相位分解反褶积方法实现了混合相位子波反褶积,在提高地震记录分辨率的同时,能自动控制高频噪声放大效应对信噪比的影响,达到信噪比和分辨率的相对和谐,更好地反映地下构造的形态特征和组合关系,可以拓宽地震记录的有效频带,突出其中的微弱构造信息。
| [1] |
伊振林, 王润秋. 一种新的混合相位反褶积方法[J].
石油地球物理勘探, 2006, 41 (3) : 266 –270.
Yi Zhenlin, Wang Runqiu. A new mixed phase deconvelotion method[J]. Oil Geophysical Prospecting, 2006, 41 (3) : 266 –270. |
| [2] |
杨培杰, 印兴耀. 地震子波提取方法综述[J].
石油地球物理勘探, 2008, 43 (1) : 123 –128.
Yang Peijie, Yin Xingyao. Summary of seismic wavelet pick-up[J]. Oil Geophysical Prospecting, 2008, 43 (1) : 123 –128. |
| [3] | Lazear G D. Mixed-phase wavelet estimation using fourth-order cumulants[J]. Geophysics, 1993, 58 (7) : 1042 –1051. DOI:10.1190/1.1443480 |
| [4] | Porsani M J, Ursin B. Mixed-phase deconvolution[J]. Geophysics, 1998, 63 (2) : 637 –647. DOI:10.1190/1.1444363 |
| [5] | Porsani M J, Ursin B. Mixed-phase deconvolution and wavelet estimation[J]. The Leading Edge, 2000, 19 (1) : 76 –79. DOI:10.1190/1.1438464 |
| [6] | Widess M B. Quantifying resolving power of seismic systems[J]. Geophysics, 1982, 47 (8) : 1160 –1173. |
| [7] | 李庆忠. 走向精确勘探的道路[M]. 北京: 石油工业出版社, 1994 . |
| [8] |
李庆忠. 地震勘探分辨率与信噪比谱的关系——答云美厚"地震分辨力新认识"一文[J].
石油地球物理勘探, 2008, 43 (2) : 244 –245.
Li Qingzhong. Relationship between resolution of seismic exploration and spectrum of S/N ratio[J]. Oil Geophysical Prospecting, 2008, 43 (2) : 244 –245. |
| [9] | Puryear C I, Castagna J P. Layer-thickness determination and stratigraphic interpretation using spectral inversion:Theory and application[J]. Geophysics, 2008, 73 (2) : R37 –R48. DOI:10.1190/1.2838274 |
| [10] | Velis D R. Stochastic sparse-spike deconvolution[J]. Geophysics, 2008, 73 (1) : R1 –R9. DOI:10.1190/1.2790584 |
| [11] |
李大卫, 尹成, 赵维坤, 等. 基于相位扫描的地震子波提取方法研究[J].
西南石油大学学报, 2007, 29 (3) : 17 –19.
Li Dawei, Yin Cheng, Zhao Weikun, et al. Seismic wavelet extraction base on phase scan[J]. Journal of Southwest Petroleum University, 2007, 29 (3) : 17 –19. |
| [12] |
崔庆辉, 芮拥军, 尚新民, 等. 混合相位地震子波提取及应用[J].
石油物探, 2011, 50 (5) : 481 –486.
Cui Qinghui, Rui Yongjun, Shang Xinmin, et al. Mixedphase seismic wavelet extraction and its application[J]. Geophysical Prospecting for Petroleum, 2011, 50 (5) : 481 –486. |
| [13] | Edgar J A, Selvage J I. Can thin bed identified using statistical phase estimation?[J]. First Break, 2011, 29 (3) : 55 –65. |
| [14] |
张宪国, 林承焰. 测井盲反褶积及在储层构型界面识别中的应用[J].
西南石油大学学报:自然科学版, 2010, 32 (2) : 63 –38.
Zhang Xianguo, Lin Chengyan. Well logging blind deconvolution and the application in reservoir textural interface[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2010, 32 (2) : 63 –38. |
| [15] |
李海山, 吴国忱, 印兴耀. 基于广义高斯分布的地震盲反褶积方法研究[J].
地球物理学进展, 2012, 27 (3) : 936 –944.
Li Haishan, Wu Guochen, Yin Xingyao. Seismic blind deconvolution method based on generalized Gaussian distribution[J]. Progress in Geophysics, 2012, 27 (3) : 936 –944. |
| [16] |
孟大江, 王德利. 基于高阶统计复倒谱子波提取[J].
物探与化探, 2013, 37 (3) : 494 –499.
Meng Dajiang, Wang Deli. Wavelet extraction based on complex ceptrum of high-order statistics[J]. Geophysical & Geochemical Exploration, 2013, 37 (3) : 494 –499. |
| [17] |
刘金俊, 王修田, 徐世浙, 等. 基于子波相位谱扫描法的子波求取方法[J].
海洋科学, 2000, 24 (6) : 4 –7.
Liu Jinjun, Wang Xiutian, Xu Shizhe, et al. A wavelet estimation method based on the wavelet phase spectrum scanning[J]. Marine Sciences, 2000, 24 (6) : 4 –7. |
| [18] |
蒋立, 谭佳, 张绪建. 同态反褶积的子波稳定性方法研究[J].
石油物探, 2012, 24 (6) : 239 –243.
Jiang Li, Tan Jia, Zhang Xvjian. Research on the methods for wavelet stability of homomorphic deconvolution[J]. Geophysical Prospecting for Petroleum, 2012, 24 (6) : 239 –243. |
| [19] |
刘洋, 李承楚. 地震资料信噪比估计的几种方法[J].
石油地球物理勘探, 1997, 32 (2) : 257 –262.
Liu Yang, Li Chengchu. Some methods for estimating the signal/noise ratio of seismic data[J]. Oil Geophysical Prospecting, 1997, 32 (2) : 257 –262. |
| [20] |
张军华, 藏胜涛, 周振晓, 等. 地震资料信噪比定量计算及方法比较[J].
石油地球物理勘探, 2009, 44 (4) : 481 –486.
Zhang Junhua, Zang Shengtao, Zhou Zhenxiao, et al. Quantitative computation and comparison of S/N ratio in seismic data[J]. Oil Geophysical Prospecting, 2009, 44 (4) : 481 –486. |
 2015, Vol. 37
2015, Vol. 37


