2. 中国石油大学(华东)CNPC测井重点实验室, 山东 青岛 266580;
3. 中国石油青海油田分公司天然气开发公司, 青海 格尔木 816000
2. CNPC Key Laboratory of Well Logging, China University of Petroleum, Qingdao, Shandong 266580, China;
3. Natural Gas Development Company, Qinghai Oilfield Company, PetroChina, Germu, Qinghai 816000, China
岩石的纵、横波速度等声学性质受温度、压力、孔隙流体性质等因素的综合影响,不同地层条件下低渗透岩石的声学参数差异较大,开展模拟地层条件下的岩石声学参数测试与分析,对研究声学参数的变化规律,进而指导油气田(特别是含气储层)的勘探开发具有重要意义。国内外学者针对该问题进行了大量的研究工作:Batzle M等[1]讨论了温度和压力的变化对岩石波速的影响,沈联蒂等[2]研究了有效覆盖压力对纵、横波速度的影响,施行觉等[3]通过实验较为系统地研究了储层条件下波速的变化规律及其影响因素,史謌等[4]研究了岩石纵、横波速度与孔隙度、泥质含量的关系。对于气层的识别目前大多是基于气层的纵、横波速度特性,以纵横波速度比[5-6]、泊松比[7-8]定性识别天然气。定量评价方面,张静等[9]采用含气特征曲线重构技术预测致密砂岩含气储层段,边会媛等[10]利用横波数据进行低孔低渗储层气层识别与储层参数的定量评价。这些方法大多是建立在含气饱和度与纵、横波时差以及孔隙度的经验拟合公式上,具有较大的局限性,适应性较差[11]。针对低渗透储层含气性定性识别、定量预测困难等问题,本文开展了模拟地层条件下的声学岩石物理实验,研究压力、孔隙流体等对岩石声学性质的影响,探索基于声波测井资料的含气性评价方法。
1 低渗透岩石声学特征实验岩样取自西部某油田低渗透气层,岩性为粉砂岩,基本物性见表 1。岩样的渗透率最大值为0.980 mD,最小值为0.050 mD,平均渗透率为0.327 mD,属于典型低渗透岩样。为研究孔隙流体和压力对岩石声学性质的影响,实验中,分别保持岩样在干燥状态、饱和水状态,并分别采用氮气和密度为0.843 g/cm3的变压器油驱替饱和水岩样至束缚水状态,测试了不同围压,不同孔隙压力,不同流体性质及饱和度下岩样纵、横波速度。数值模拟基于Krief理论[12],建立砂岩模型,骨架矿物为石英,密度为2.650 g/cm3,体积模量38.2 GPa,剪切模量42.7 GPa,孔隙流体为气和水,其体积模量分别为0.07 GPa、2.73 GPa。
| 表1 实验岩样基础数据 Table 1 The basic data of experimental samples |
国内外实验研究和理论分析证明岩石的纵、横波速度与孔隙度成反比,并且这一理论在很多油田得以实际的应用。根据威利平均时间公式
| $ \Delta t = (1 - \phi )\Delta {t_{\rm{ma}}} + \phi \Delta {t_{\rm{f}}} $ | (1) |
式中:Δt——纯岩石的声波时差,μs/m;Δtma——岩石骨架的声波时差,μs/m;Δtf——孔隙流体的声波时差,μs/m;φ——纯岩石的孔隙度,无因次。对于岩性一定、孔隙度一定的岩样,纵波时差取决于孔隙流体。
根据Krief在1990年提出的岩石弹性模型,经数值计算可以看出,含水饱和度90%左右时,纵波速度(vP)增加明显。由于横波速度
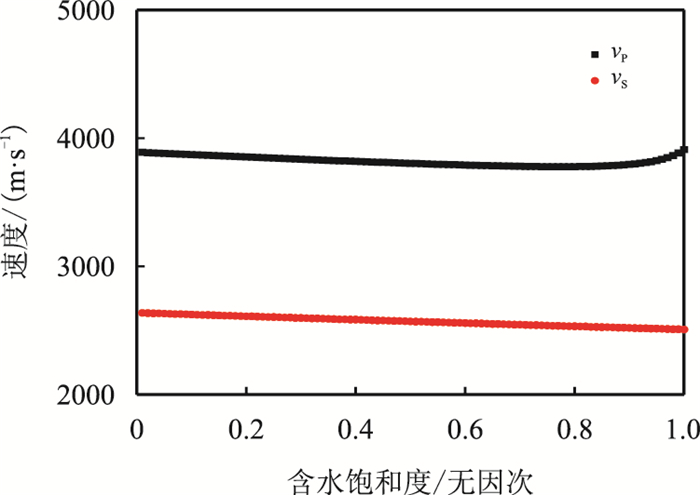 |
| 图1 波速与含水饱和度数值计算结果 Fig. 1 Plot of wave velocity vs water saturation based on numerical simulation |
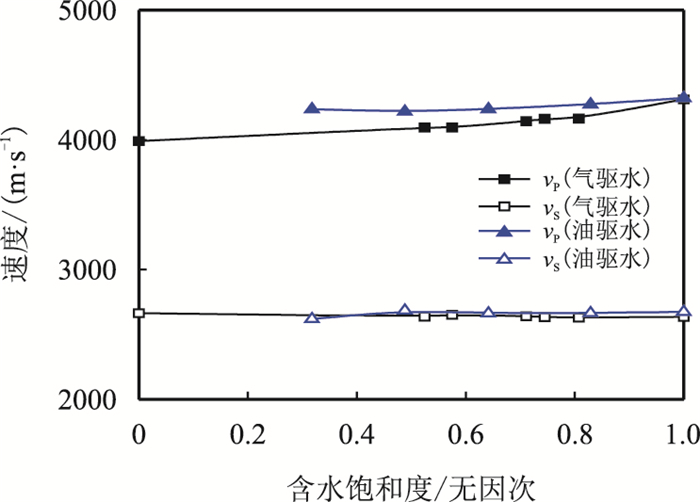 |
| 图2 8号岩芯波速与含水饱和度关系 Fig. 2 Plot of wave velocity vs water saturation of sample 8 |
由实验结果可知,含不同流体的岩石其纵、横波速度有一定差别,纵波速度与含水饱和度成正比,干燥砂岩纵波速度最低,饱含水时最高,含水饱和度在90%左右时纵波速度变化幅度最大。在油驱水过程中,纵波速度随含水饱和度的减小呈略微减小趋势,其值大于气驱水的情况。孔隙流体的性质及饱和程度对横波速度影响较小,总体上随含气饱和度的增大横波速度略有增大。
1.1.2 孔隙流体对岩石弹性模量的影响岩石的弹性性质受孔隙结构、固体相以及流体的综合影响,定量研究弹性参数变化特征对深入了解岩石性质、分析孔隙流体性质等具有重要意义[13]。图 3、图 4分别为围压为零时,气驱水过程中剪切模量、杨氏模量、体积模量、泊松比等参数与含水饱和度的关系曲线。从图中可知,随着含水饱和度的增大,泊松比、杨氏模量及体积模量增加,剪切模量基本不变,泊松比对孔隙流体性质及饱和程度最为敏感,说明该参数可用于含气饱和度的定性指示。
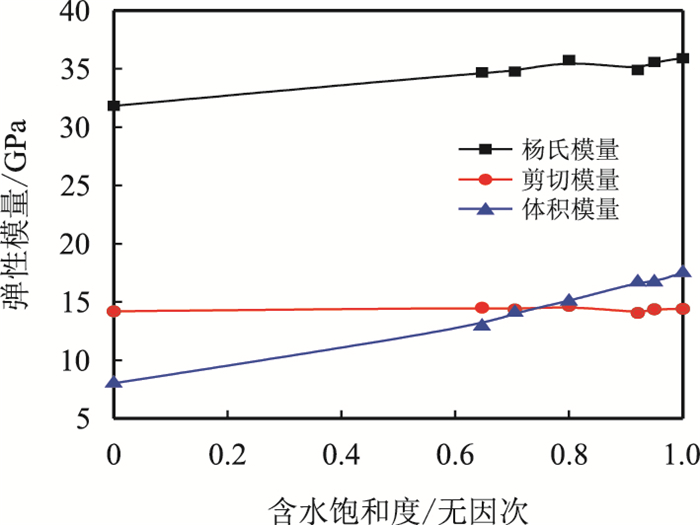 |
| 图3 2号岩芯弹性模量与含水饱和度的关系 Fig. 3 Plot of elasticity modulus vs $S_{\rm{w}}$ of sample 2 |
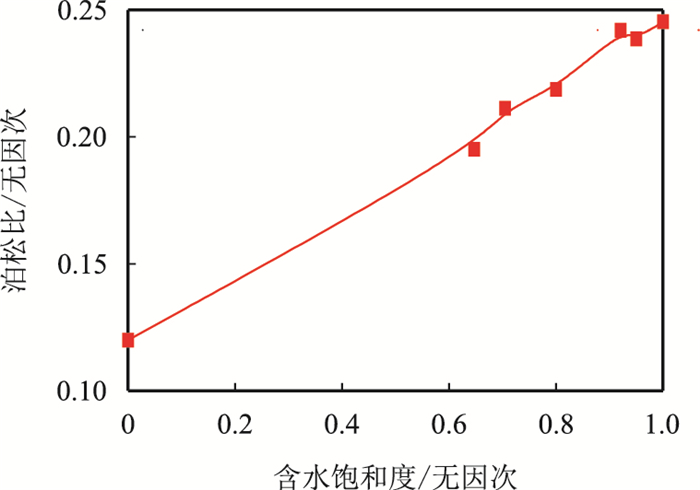 |
| 图4 2号岩芯泊松比与含水饱和度的关系 Fig. 4 Plot of poisson ratio vs $S_{\rm{w}}$ of sample 2 |
在地层中存在两种不同压力(上覆地层压力和孔隙流体压力),它们共同影响地层的纵、横波速度[14]。图 5、图 6为未施加孔隙压力时岩石纵、横波速度与围压的关系。由图可知,在一定的压力范围内,无论何种孔隙流体,岩石纵、横波速度均与围压成正比,但不呈严格的线性关系。在围压相对较小时,孔隙的闭合效应明显,速度对围压较为敏感,岩石的波速随围压增加较快。随着围压的增大,孔隙的闭合效应减弱,岩石速度随围压变化逐渐趋于线性、平缓。岩石的闭合效应受岩性、孔隙结构、孔隙流体性质等因素的影响,因此,不同岩样的声波速度随围压的变化关系也有所不同,从图中可以看出,岩石含气饱和度越高,纵、横波速度对压力的变化越敏感。
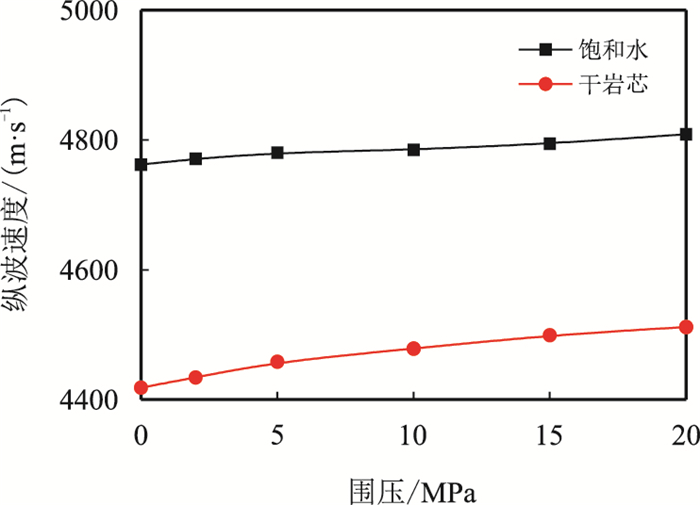 |
| 图5 5号岩样纵波速度与围压的关系 Fig. 5 Plot of Pv vs confining pressure of sample 5 |
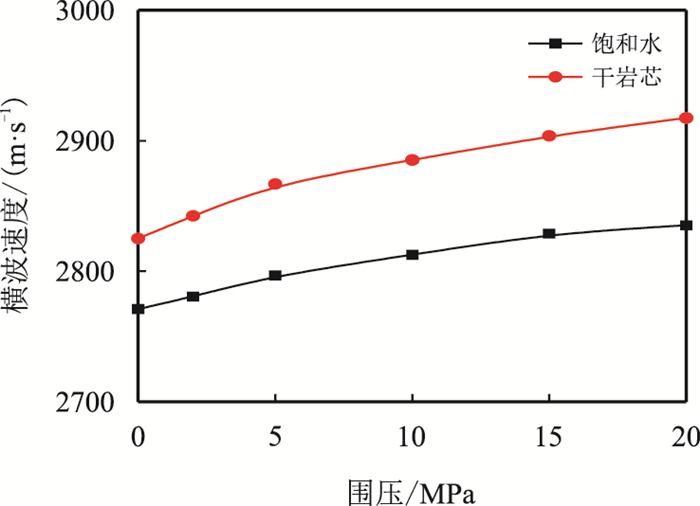 |
| 图6 5号岩样横波速度与围压的关系 Fig. 6 Plot of vS vs confining pressure of sample 5 |
地层中岩石受到上覆地层压力和孔隙流体压力的共同作用,岩石受到的有效压力(pe)可视为上覆地层压力(pe)和孔隙流体压力(pf)之差,即
| $ p_{\rm{e}} = p_{\rm{s}}-p_{\rm{f}} $ | (2) |
本文实验中,围压(ps)与孔隙压力(pf)之差即岩样受到的有效压力。图 7~图 10分别为干燥岩样纵、横波速度与孔隙压力、有效压力的关系,由图可知,岩样纵、横波速度随孔隙压力增大而减小,随有效压力的增大而增大。围压一定时,孔隙压力增大,有效压力减小,岩石骨架膨胀,微孔隙张开,声波传播路径增大,声速减小,可以此来识别异常高压地层。
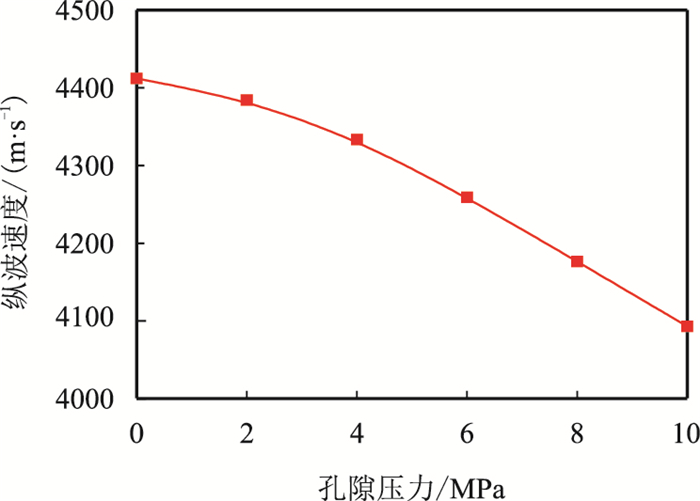 |
| 图7 6号干样纵波速度与孔隙压力的关系(围压20 MPa) Fig. 7 Plot of vP vs pore pressure of dry sample 6(ps=20 MPa) |
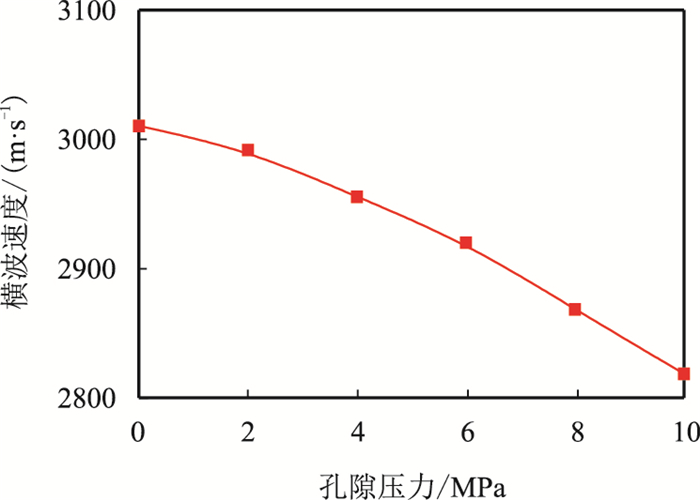 |
| 图8 6号干样横波速度与孔隙压力的关系(围压20 MPa) Fig. 8 Plot of vS vs pore pressure of dry sample 6(vs=20 MPa) |
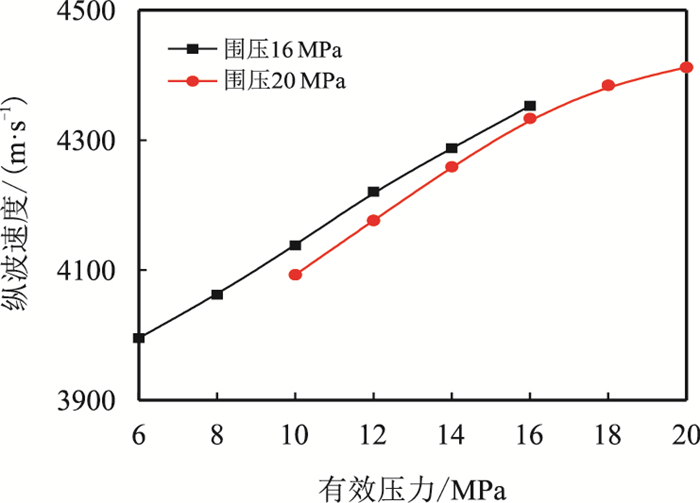 |
| 图9 6号干样纵波速度与有效压力的关系 Fig. 9 Plot of vP vs effective pressure of dry sample 6 |
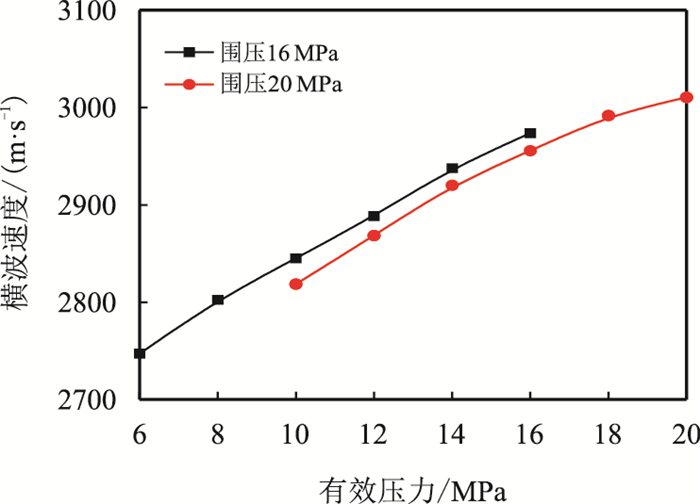 |
| 图10 6号干样横波速度与有效压力的关系 Fig. 10 Plot of vS vs effective pressure of dry sample 6 |
图 11分别为利用实验室测得的孔隙度与饱和水、束缚水及干燥状态下岩样纵、横波速度的关系。从图中可以看出,不同流体状态下岩石纵、横波速度均与孔隙度成反比,两者呈较好的线性关系(表 2)。从拟合结果可知,孔隙中流体性质及含量对岩石纵、横波速度的影响较大,不同流体状态下岩石纵、横波速度与孔隙度的关系不同。这表明:如果在含气储层的孔隙度建模中,单纯应用“岩芯刻度测井”建立孔隙度与声波速度的关系进行储层孔隙度预测,势必造成一定误差。但是,可以利用这一性质进行基于声学参数的流体性质识别与预测。
| 表2 粉砂岩岩样纵、横波速度与孔隙度拟合关系(围压为零) Table 2 Fit results of P-and S-wave velocity and porosity under different water conditions without confining pressure |
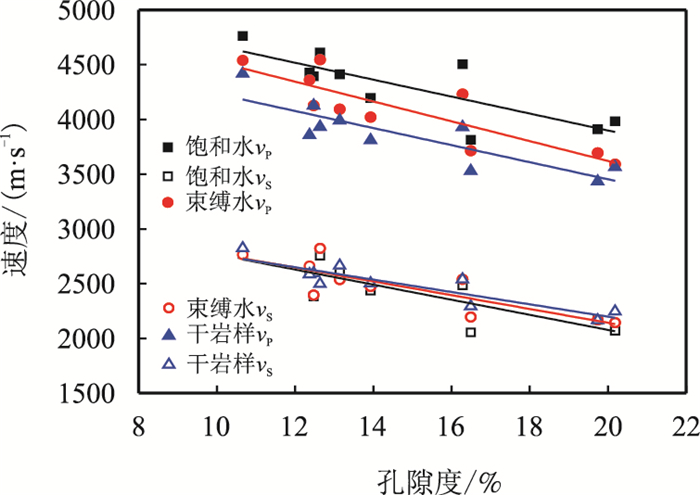 |
| 图11 纵、横波速度与孔隙度的关系(围压为零) Fig. 11 Plot of P-and S-wave velocity vs porosity without confining pressure |
分别研究了岩样在饱和水、干燥状态及气驱水至束缚水状态时纵、横波速度之间的关系(常温常压环境),如图 12所示。3种状态下岩石的纵、横波速度均呈现较好的线性关系,拟合的斜率和截距与岩样所含的流体性质有关。实验结果与根据Krief(1990)模型进行的数值模拟结果(图 13)关系一致,验证了其准确性。纵、横波拟合关系式如表 3所示。根据纵、横波速度拟合关系,可以预测该地区的横波速度,用于测井和地震资料的解释处理。
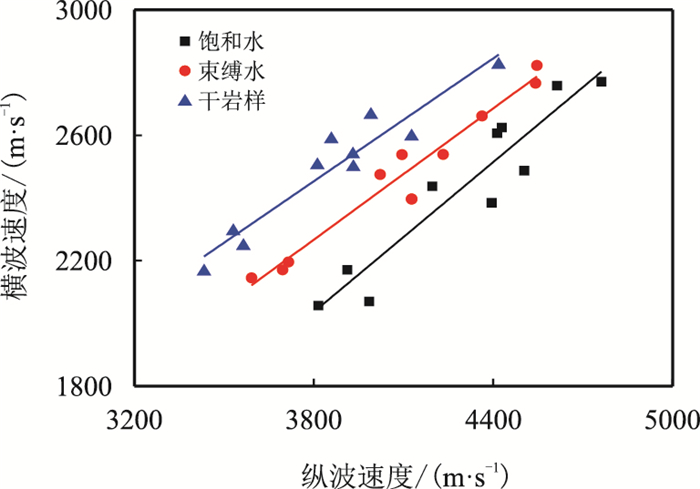 |
| 图12 实验所得的纵、横波速度关系 Fig. 12 Relation between vP and vS based on experimental data |
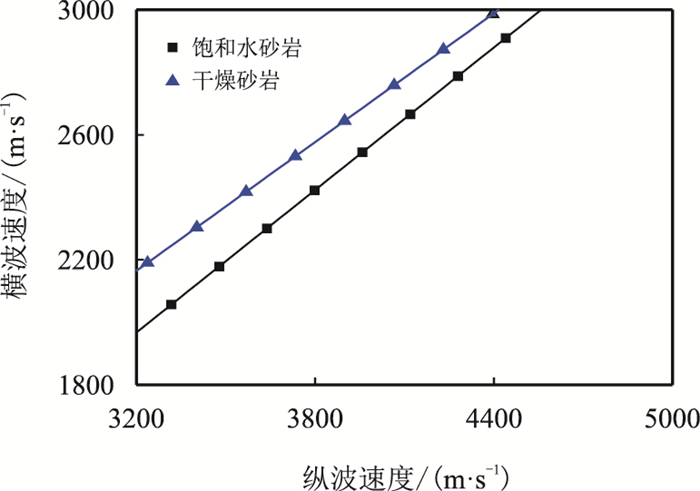 |
| 图13 数值计算的纵、横波速度关系 Fig. 13 Relation between vP and vS based on numerical simulation |
| 表3 不同状态下岩样纵、横波速度的拟合关系 Table 3 The linear relation between vP and vS under different water conditions |
由实验结果可知,岩石在不同流体状态下的声波速度及弹性参数具有一定差异,将这些差异进行对比分析,提取流体敏感因子,建立相关图版即可进行储层含气性的定性识别与评价。本文基于实验和数值模拟结果,研究了纵横波速度比-波阻抗交会和纵、横波速度平方交会截距两种含气性识别与评价的方法。
2.1 纵、横波速度比-波阻抗交会法图 14是岩样在饱和水、干燥状态及气驱水至束缚水状态时纵、横波速度比与波阻抗交会图,从图中可以看出,干燥状态下数据点分布在交会图的左下方,随着含气饱和度降低,纵、横波速度比与波阻抗逐渐增大,气水相(气油相或者气水油相)、油水相(油相或水相)的数据点依次向右上方迁移。不同孔隙流体下的数据点分布在不同的区域,因而可以利用二者的交会图识别孔隙流体性质。
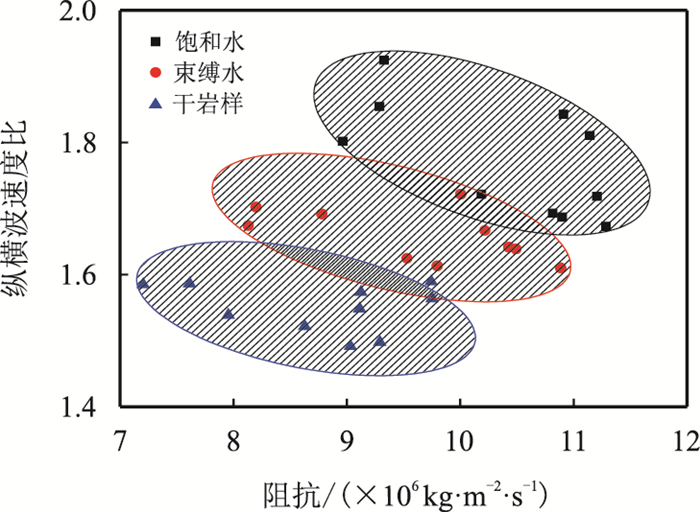 |
| 图14 纵、横波速度比与波阻抗交会图(常温常压) Fig. 14 Plot of P-and S-wave velocity vs wave impedance at normal temperatures and pressures |
岩石的体积模量与纵、横波速度及密度的关系为
| $ K = \rho v_{\rm{P}}^2 - \dfrac{4}{3}\rho v_{\rm{S}}^2 $ | (3) |
式中:K——岩石的体积模量,GPa;vP——纵波速度,m/s;vS——横波速度,m/s;ρ——岩石的密度,g/cm3。
对式(3)做如下变换
| $ v_{\rm{P}}^2 = \dfrac{K}{\rho } + \dfrac{4}{3} v_{\rm{S}}^2 $ | (4) |
由式(4)可知,孔隙流体不同,岩石的纵、横波速度交会拟合有不同的截距。根据实验结果,岩石体积模量随含气饱和度的增大而减小,且其变化幅度大于体积密度的变化幅度,故式(4)中常数项随含气饱和度的增加而减小。
图 15、图 16分别为实验结果和数值模拟结果纵、横波速度平方交会图,表 4为拟合结果。从图 15、图 16和表 4可知,实验数据和数值模拟规律一致,含气饱和度越高,纵、横波速度平方关系式的截距越小,因而可以通过对比其截距判断储层的含气性。
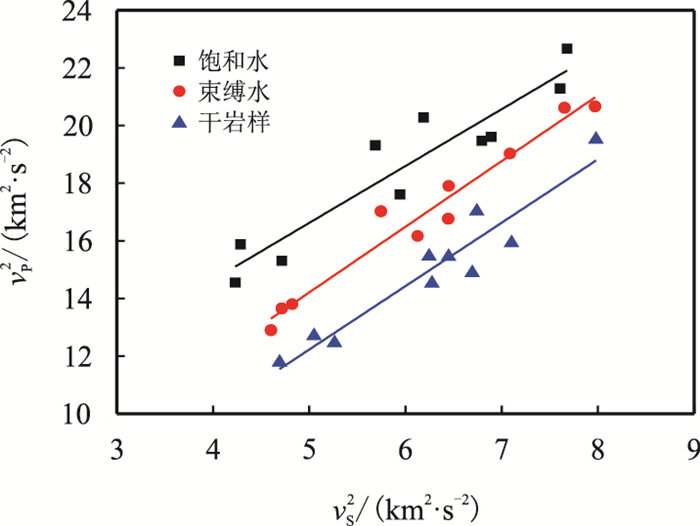 |
| 图15 实验值纵、横波速度平方交会图 Fig. 15 Plot of $v^2_{\rm{P}}$ vs $v^2_{\rm{S}}$ based on experimental data |
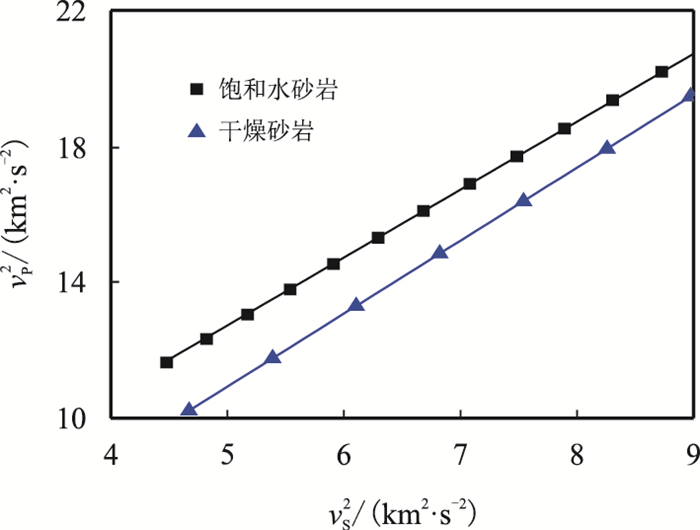 |
| 图16 数值模拟纵、横波速度平方交会图 Fig. 16 Plot of $v^2_{\rm{P}}$ vs $v^2_{\rm{S}}$ based on numerical simulation |
| 表4 纵、横波速度平方关系拟合结果 Table 4 Fit results of $v_{\rm{P}}^2$ and $v_{\rm{S}}^2$ |
(1) 岩石的声学性质受孔隙度、压力、流体性质等因素的综合影响。围压一定时随含水饱和度的增大,岩石纵波速度增大,横波速度变化不明显,泊松比、杨氏模量及体积模量增加,剪切模量基本不变。含水饱和度相同时,岩石孔隙流体为气水两相时的纵波速度小于油水两相时的纵波速度。
(2) 不同孔隙流体下岩石纵、横波速度均随围压增加而增大,在压力较小时,声速增加较快,随着围压变大,声速随围压变化逐渐趋于线性、平缓。围压一定时孔隙压力增大,纵、横波速度减小。
(3) 纵、横波速度比-波阻抗交会和纵、横波速度平方交会截距在低渗透岩石含气性评价中起着重要作用。随着含气饱和度的增大岩石纵、横波速度比、波阻抗及纵、横波速度平方交会图的截距都明显增加,以此进行含气性评价,可提高利用声波测井资料对储层流体进行评价的能力。
| [1] | Batzle M, Wang Z. Seismic properties of pore fluids[J]. Geophysics, 1992, 57 : 1385 –1407. |
| [2] |
沈联蒂, 史謌. 岩性、含油气性、有效覆盖压力对纵、横波速度的影响[J].
地球物理学报, 1994, 37 (3) : 391 –399.
Shen Liandi, Shi Ge. Effect of lithologic character, petroleum and effective overburden pressure on compressional wave and shear wave velocity[J]. Chinese Journal of Geophysics, 1994, 37 (3) : 391 –399. |
| [3] |
施行觉, 夏从俊, 吴永刚. 储层条件下波速的变化规律及其影响因素的实验研究[J].
地球物理学报, 1998, 41 (2) : 234 –241.
She Xingjue, Xia Congjun, Wu Yonggang. The laboratory study on wave velocity under reservoir condition and its affection factors[J]. Chinese Journal of Geophysics, 1998, 41 (2) : 234 –241. |
| [4] |
史謌, 杨东全. 岩石波速和孔隙度、泥质含量之间的关系研究[J].
北京大学学报:自然科学版, 2001, 37 (3) : 379 –384.
Shi Ge, Yang Dongquan. The regression analysis study on velocity and porisity, and clay content of rocks[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2001, 37 (3) : 379 –384. |
| [5] | 楚泽涵. 声波测井原理[M]. 北京: 石油工业出版社, 1987 . |
| [6] |
肖万春. 影响纵、横波速度的几种因素[J].
油气藏评价与开发, 1985 (6) : 57 –63.
Xiao Wanchun. Several influencing factors of longitudinal and shear wave velocity[J]. Progress in Exploration Geophysics, 1985 (6) : 57 –63. |
| [7] |
樊长江, 王贤. 泊松比岩性预测方法研究——以准噶尔盆地为例[J].
石油勘探与开发, 2006, 33 (3) : 299 –302.
Fan Changjiang, Wang Xian. Lithology prediction by Poisson's ratio:An example from Junggar Basin, NW China[J]. Petroleum Exploration and Development, 2006, 33 (3) : 299 –302. |
| [8] | Brie A, Pampuri F, Marsala A F, et al. Shear sonic interpretation in gas-bearing sands[C]. SPE 30595, 1995. |
| [9] |
张静, 张虎权, 李延丽, 等. 蜀南地区须家河组致密砂岩含气性综合预测[J].
天然气工业, 2009, 29 (1) : 45 –47.
Zhang Jing, Zhang Huquan, Li Yanli, et al. Gas bearing prediction on tight sandstone gas reservoirs of Xujiahe Formation in south Sichuan Basin[J]. Natural Gas Industry, 2009, 29 (1) : 45 –47. |
| [10] |
边会媛, 潘保芝. 利用横波数据进行低孔低渗储层气层识别与储层参数定量评价[J].
吉林大学学报:地球科学版, 2010, 40 (S1) : 106 –109.
Bian Huiyuan, Pan Baozhi. Gas identification and quantitative evaluation of low porosity and low permeability reservoir parameters using dipole shear wave data[J]. Journal of Jilin University:Earth Science Edition, 2010, 40 (S1) : 106 –109. |
| [11] |
王磊, 王学琴, 吴胜, 等. 利用弹性模量计算含气饱和度方法研究[J].
西南石油大学学报:自然科学版, 2011, 33 (4) : 69 –72.
Wang Lei, Wang Xueqin, Wu Sheng, et al. Method of gas saturation prediction by elastic modules[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2011, 33 (4) : 69 –72. |
| [12] | Krief M, Garat J, Stellingwerff J, et al. A petrophysical interpretation using the velocities of P and S waves (full-waveform sonic)[J]. The Log Analyst, 1990, 31 : 355 –369. |
| [13] |
杜韫华, 钱凯, 张守鹏, 等. 中国天然气储层的岩石、古地理类型与勘探方向[J].
石油与天然气地质, 1999, 20 (2) : 140 –143.
Du Yunhua, Qian Kai, Zhang Shoupeng, et al. Exploration orientation and rock, palaeogeographic types of Chinás gas reservoirs[J]. Oil & Gas Geology, 1999, 20 (2) : 140 –143. |
| [14] |
史謌, 沈联蒂. 根据波速-压力关系评价岩石岩性、物性的实验研究[J].
地球物理学报, 1990, 33 (2) : 212 –219.
Shi Ge, Shen Liandi. Evaluations of the physical property of rocks from the relation between wave velocity and pressure:An experimental study[J]. Chinese Journal of Geophysics, 1990, 33 (2) : 212 –219. |
 2015, Vol. 37
2015, Vol. 37


