水下作业的海洋立管,是整个海油集输通道,其工作环境复杂,经常受到洋流、波流、激荡振动等动态载荷的影响,引起立管的振动甚至引起立管的共振。立管的振动不仅影响到立管的工作稳定性还影响到立管疲劳寿命,因此了解结构的固有频率与振型,可为防止结构共振破坏、振动疲劳[1]以及评价结构的动态特性和优化结构设计提供一定的依据。所谓模态分析就是为了求特征值和特征向量,特征值也即结构振动的振型对应的频率。通常进行的模态分析都是在空气中进行的,由于空气密度小,对计算结果影响小,在计算时通常忽略了空气的作用,默认为在真空条件进行分析计算的。对于受到液体作用的结构,由于液体密度相对空气密度大,在进行模态分析要考虑液体与固体之间的耦合作用。将默认的真空条件下进行的模态分析称为干模态分析,考虑了液固耦合作用模态计算的称为湿模态分析[2]。很多文章在研究水下结构动态响应时,通常忽略了液体对结构的影响,直接采用干模态分析,得出结果与实际情况不相符。本文为进一步研究水结构的动态响应,采用了Workbench Acoustic Extension分析模块对海洋立管进行水下模态分析,得到结构的前12阶固有频率与振型。通过振型的研究,对结构进行了优化,得出优化结果。
1 模态分析理论由经典力学理论可知,物体的动力学通用方程为
| ${\boldsymbol{{M}}} {{\boldsymbol{{x}}} ''} + {\boldsymbol{{C}}} {{\boldsymbol{{x}}} '} + {\boldsymbol{{K}}} {\boldsymbol{{x}}} = {{\boldsymbol{{F(t)}}} } ^{\left[{2-11} \right]}$ | (1) |
式中:
无阻尼模态分析是经典的特征值问题,动力问题的运动方程如下
| ${\boldsymbol{{M}}}{\boldsymbol{{x}}}" + {\boldsymbol{{K}}}{\boldsymbol{{x}}} = 0$ | (2) |
本文分析对象为水下作业的海洋立管,由于其结构阻尼较小,在忽略其对固有频率和振型的同时还考虑液体对结果的耦合作用,其计算方程为
| ${{\boldsymbol{{M}}} + {\boldsymbol{{M}}}_{\rm{w}}} {{\boldsymbol{{x}}}''} + {{\boldsymbol{{K}}} + {\boldsymbol{{K}}}_{\rm{w}}} {\boldsymbol{{x}}} = 0$ | (3) |
式中:
式(3)也即所谓的虚拟质量法[4]求解模态的方程式。
在Workbench Design Molder中建立三维几何模型。所建模型由海水、立管和原油3部分组成。立管内腔由原油填充,外壁由海水包裹。立管的材料为API5LX52,外径为325.85 mm,壁厚10.30 mm,受计算机计算能力的限制,取立管长度为15 000 mm。采用Enclo-sure命令所建立海水模型为3 000 mm×3 000 mm×24 000 mm的立方体。用Fill 命令建立油系模型为直径305.25 mm,长15 000 mm的圆柱体。完成水系和油系模型建立后,再将模型合并成一新体,其目的是在划分网格时使两者公共面处节点位置重合[5],避免网格划分过程中出现网格干涉问题。图 1为几何模型。
 |
| 图1 几何模型 Fig. 1 Geometric model |
Workbench中提供了平面和立体两类网格划分类型。平面模型提供了两种单元(三角形单元和四边形单元),4种方法:自动划分、三角形、均匀四边形与三角形和均匀四边形。立体模型提供了4种类型(四面体,棱锥,棱柱,六面体)和6种方法:Automatic(自动划分)、Hex Dominant(六面体优)、Sweep(扫掠)、MultiZone(多区域)、Tetrahedrons(四面体)和Cartesion(笛卡尔)。立管和原油均采用六面体网格(图 2)和液体模型采用面印射网格。其中立管重点分析,网格需加密,设置立管网格尺寸为0.08 m,液体网格尺寸为0.30 m,细化液体与固体耦合处网格。图 3为立管、原油和海水的有限元模型。
 |
| 图2 立管网格 Fig. 2 The mesh of riser |
 |
| 图3 模型网格剖面图 Fig. 3 The sectional mesh view of the model |
建立API5LX52、原油以及海水材料属性。API5LX52最小屈服强度为358 MPa,抗拉强度为455 MPa,密度
立管底端为固定约束,顶端为铰链约束。海水模型与原油模型定义为Acoustic-Body。分别定义声速为1 500 000 mm/s和1 350 000 mm/s。定义算法为:Coupled with sym-metry。立管内壁施压:3.0 MPa(原油采集过程对立管内壁的最大压力)。定义重力加速度:9.8 m/s2;定义立管流固耦合面;设定求解阶数:12。定义完成后开始湿模态分析。湿模态分析完成后,将海水和原油模型抑制掉,然后进行干模态分析[13-20]。
2.4 计算结果按照湿模态与干模态计算顺序,分别建立两种状态下的计算结果。表 1与表 2分别为湿模态和干模态计算的12阶固有频率与各阶频率对应的最大振幅和相应振型。图 4~图 9为截取的立管湿模态第2、4、6、8、10、12阶固有频率对应的振型云图,图 10~图 15为截取干模态第2、4、6、8、10、12阶固有频率对应的振型云图。
| 表1 湿模态前12阶分析结果 Table 1 The top 12 order of wet modal analysis results |
| 表2 干模态前12阶分析结果 Table 2 The top 12 order of dry modal analysis results |
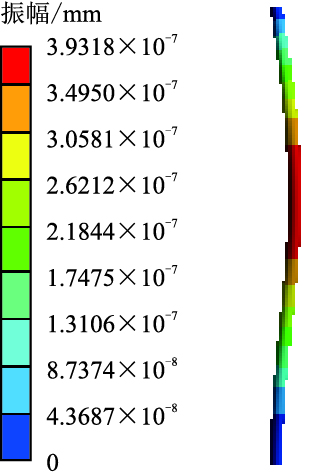 |
| 图4 第2阶湿模态振型云图 Fig. 4 2nd-order wet modal shape cloud |
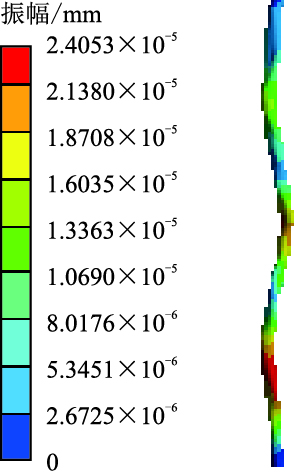 |
| 图5 第4阶湿模态振型云图 Fig. 5 4th-order wet modal shape cloud |
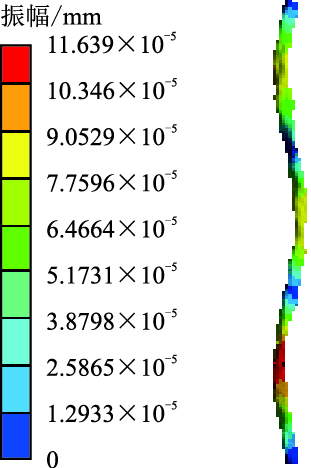 |
| 图6 第6阶湿模态振型云图 Fig. 6 6th-order wet modal shape cloud |
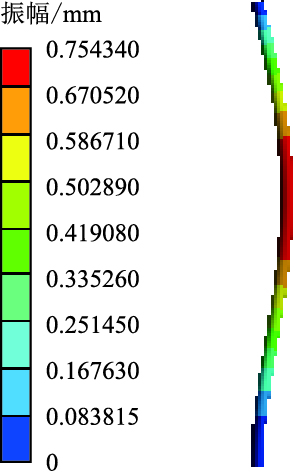 |
| 图7 第8阶湿模态振型云图 Fig. 7 8th-order wet modal shape cloud |
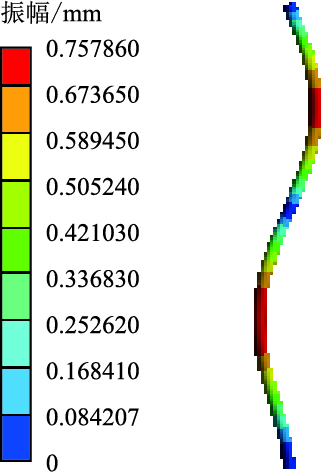 |
| 图8 第10阶湿模态振型云图 Fig. 8 10th-order wet modal shape cloud |
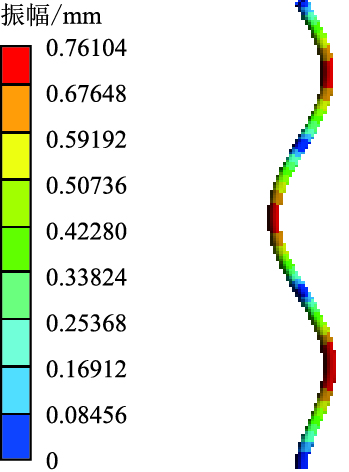 |
| 图9 第12阶湿模态振型云图 Fig. 9 12th-order wet modal shape cloud |
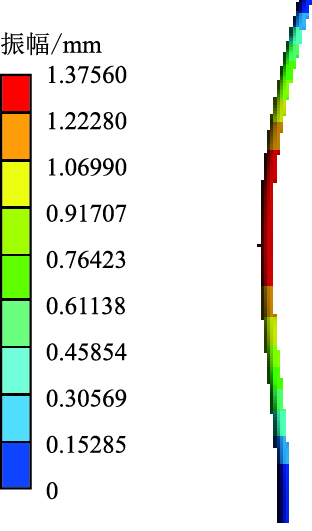 |
| 图10 第2阶干模态振型云图 Fig. 10 2nd-order dry modal shape cloud |
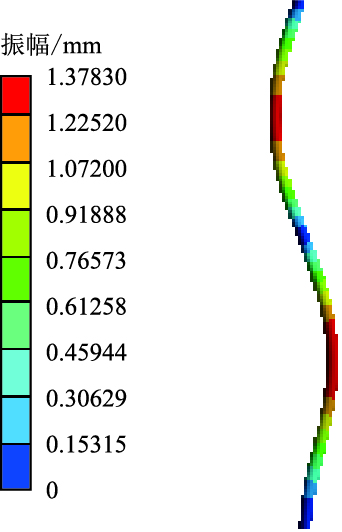 |
| 图11 第4阶干模态振型云图 Fig. 11 4th-order dry modal shape cloud |
 |
| 图12 第6阶干模态振型云图 Fig. 12 6th-order dry modal shape cloud |
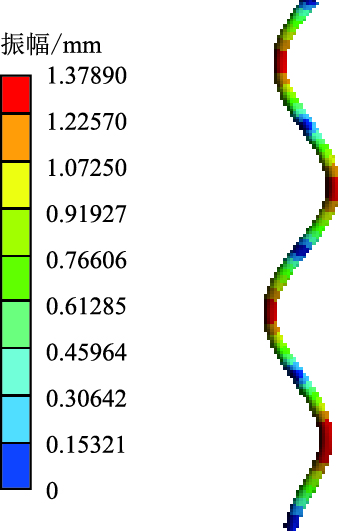 |
| 图13 第8阶干模态振型云图 Fig. 13 8th-order dry modal shape cloud |
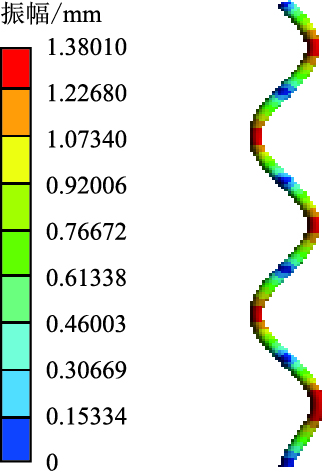 |
| 图14 第10阶干模态振型云图 Fig. 14 10th-order dry modal shape cloud |
 |
| 图15 第12阶干模态振型云图 Fig. 15 12th-order dry modal shape cloud |
通过采用虚拟质量法,综合考虑流体与固体之间的耦合作用,得出湿模态分析结果。表 1与表 2中的频率数据均按由小到大的顺序排列。比较两表中的数据可以看出,湿模态各阶固有频率比干模态各级阶固有频率小很多,干模态的第1阶固有频率是湿模态第1阶固有频率的562.0倍,干模态第12阶固有频率是湿模态第12阶固有频率的4.6倍。表 1湿模态的固有频率数据说明在液体环境中,低频载荷也会使得结构发生共振,但是这类共振对结构不会产生破坏。表 2说明干模态结构发生共振时,载荷频率要比湿模态结构高很多,相比之下湿模态结构更易发生振动。随着计算固有频率阶数的增长,两者固有频率的差值逐渐减小。
湿模态振型相对简单,同阶振幅比干模态小。湿模态振型图中第2阶振型最大变形靠近立管中部,在低频振动下符合杆状结构的振动规律;第4阶振动频率高于第2阶,立管三次弯振附加轻微的扭振,振型较第2阶复杂,弯振强度由底端向顶端减弱;由于第6阶固有频率与第4阶接近,所以立管振型基本一致;第8、10、12阶都是弯振,随着振动频率增加,振幅变大,振型变得也越来越复杂。干模态振型也是以弯振为主,振型较单一,在第2、4、6、8、10阶频率作用下共振立管弯振依次增加,随固有频率的增大,振幅逐渐变大。由湿模态与干模态振型云图可知,共振频率决定振型特性。随着各自固有频率的增大,立管的振幅在整体上有增长的趋势,振型以弯振为主,弯振次数也越来越多。在低频激励作用下,结构有轻微的扭动倾向,但振幅非常小,弯振对结构稳定性起决定作用。
3 优化设计通过分析结果得知立管结构在低频振动下发生不同程度的多处变形,其中弯振较多。当立管的刚度一定时,在不改变结构条件下,可以通过添加阻尼器避免一定频率范围的共振。本文通过在立管外壁增焊强环圈,优化立管结构,来避免立管高频共振的大变形现象。加强圈厚8 mm,宽400 mm。每段加强圈焊接位置相隔3 000 mm,将立管均分为5段,从左往右依次为第1段、第2段、第3段、第4段、第5段。图 16为优化后的立管模型。表 3为优化后计算结果。
从计算结果可看出,频率数据按照由小到大的顺序排列,随着频率的增大,振型变得也越来越复杂。立管优化后各阶振动频率变得很小,各阶频率之间的差值减小,最大频率为第12阶的2.405 8 Hz,为优化前第12阶立管振动频率的1/35.5。通过观察振型可看出,各阶立管的整体变形非常小,最大变形为0.632 8 mm,比优化前的数值要小,并且发生较大变形的管段均避开了加强部位。立管的振型与优化前相比弯振减少,扭振和径向胀缩振型增多,但立管整体变形相对均匀,振型变得简单,振幅也相对减小,从而说明了结构整体刚度较好,加强圈起到了提高整体刚度的作用,改进后的结构确实对结构的抗振性能起到优化作用,进而说明了模态分析为实现结构的优化设计提供了一定的依据。
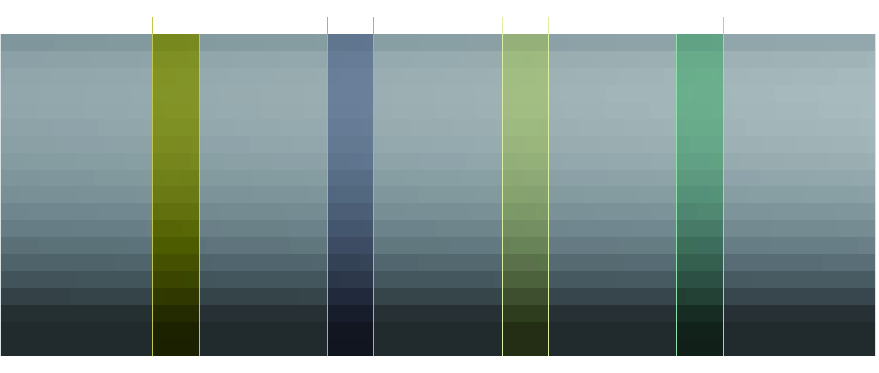 |
| 图16 立管优化后的模型 Fig. 16 The optimized riser model |
| 表3 优化后的立管湿管模态计算结果 Table 3 The top 12 order of wet modal calculation results of the optimized riser |
笔者采用Workbench自带模块Design Molder准确地建立三维模型,实现模型与模态分析模块的无缝连接,提高了计算的精度,使得计算结果也更加形象直观。通过对模态的分析计算以及优化设计,对模态的概念有了更深层的理解。
(1)文中以海洋立管湿模态分析为例,介绍了湿模态建模方法与技巧,采用Workbench Acoustic-Body模块对立管进行了湿模态分析,避免了命令流编程求解模态的不便。
(2)通过湿模态与干模态分析对比,说明湿模态在模态计算中的不可替代性。由计算结果可看出,随着模态计算的深度,振动频率越来越大,振型越来越复杂,湿模态与干模态的差异也越来来越明显。高频振动要比低频振动对立管振动的影响大,固有频率越高其振动越剧烈,对结构影响就越明显,因此高阶振型对立管的动态特性起着关键作用。故应尽量避开外界载荷频率过高对结构产生共振破坏。
(3)根据计算结果,可采取一定预防措施来避免或减小共振。如在共振区薄弱部位将结构加强或增装阻尼器或避开与结构产生共振的载荷等。
(4)结构优化后避开共振区域,证明了优化可行性,对工程具有较好的参考价值。
(5)由于受计算机计算能力限制,进行湿模态分析截取立管长度为15 000 mm,分析海洋立管工况是在全浸段,即管段全部沉浸于海水中,不包括立管的海底土壤区、全浸区、潮差区、浪溅区以及海洋大气区。虽然计算结果不能完全反映立管整体的真实动态响应,但对海洋立管系的动态特性研究具有一定的参考作用。
| [1] |
姚起杭, 姚军. 工程结构的振动疲劳问题[J].
应用力学学报, 2006, 23 (1) : 12 –15.
Yao Qihang, Yao Jun. Vibration fatigue in engineering structures[J]. Chinese Journal of Applied Mechanics, 2006, 23 (1) : 12 –15. |
| [2] | 陈艳霞, 陈磊. ANSYS Workbech工程应用与案例精通[M]. 北京: 电子工业版社, 2012 . |
| [3] |
袁安富, 陈俊. ANSYS在模态分析中的应用[J].
制造技术与机床, 2007 (8) : 79 –82.
Yuan Anfu, Chen Jun. Application of ANSYS in model analysis[J]. Manufacturing Technology & Machine Tool, 2007 (8) : 79 –82. |
| [4] |
刘晓欧, 尹韶平, 严光洪. 基于MSC Nastran的水下环肋圆柱壳体振动模态计算方法[J].
计算机辅助工程, 2006, 15 (S) : 124 –127.
Liu Xiao'ou, Yin Shaoping, Yan Guanghong. Underwater vibration modal calculation of the ring-stiffened cylindrical shell with MSC Nastran[J]. Computer Aided Engineering, 2006, 15 (S) : 124 –127. |
| [5] | 李兵, 何正嘉, 陈雪峰. ANSYS Workbench设计仿真优化[M]. 北京: 清华大学出版社, 2013 . |
| [6] | 张立翔. 流体结构互动理论及其应用[M]. 北京: 科学出版社, 2004 . |
| [7] |
仲维国, 张嘉钟. 水模态的ANSYS有限元分析[J].
强度与环境, 2004, 31 (1) : 17 –21.
Zhong Weiguo, Zhang Jiazhong. Finite element analysis of missile's calm-water modes using ANSYS[J]. Structure & Environment Engineering, 2004, 31 (1) : 17 –21. |
| [8] |
杨康, 韩涛. ANSYS在模态分析中的应用[J].
佳木斯大学学报:自然科学版, 2005, 23 (1) : 81 –84.
Yang Kang, Han Tao. The application of ANSYS in model analysis[J]. Journal of Jiamusi University:Natural Science Edition, 2005, 23 (1) : 81 –84. |
| [9] |
曹银萍, 石秀华. 基于ANSYS的鱼雷有限元建模与模态分析[J].
弹箭与制导学报, 2009, 29 (3) : 289 –292.
Cao Yinping, Shi Xiuhua. Finite element modeling and modal analysis of torpedo based on ANSYS[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2009, 29 (3) : 289 –292. |
| [10] |
贾锐, 石秀华, 徐宇明, 等. 基于ANSYS的圆柱薄壳结构模态分析[J].
弹箭与制导学报, 2008, 28 (6) : 314 –316.
Jia Rui, Shi Xiuhua, Xu Yuming, et al. Modal analysis on cylindrical filmy shell structure based on ANSYS[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2008, 28 (6) : 314 –316. |
| [11] |
杨新文, 和振兴. 梯形轨枕轨道振动特性研究[J].
振动工程学报, 2012, 25 (4) : 388 –393.
Yang Xinwen, He Zhenxing. Vibration characteristics of ladder sleeper track[J]. Journal of Vibration Engineering, 2012, 25 (4) : 388 –393. |
| [12] |
陈军明, 黄玉盈. 水下环向双周期加肋圆柱壳体的自由振动[J].
应用力学学报, 2004, 21 (1) : 40 –43.
Chen Junming, Huang Yuying. Free vibration of doubly periodic ring stiffened infinite cylindrical circular shell in water[J]. Chinese Journal of Applied Mechanics, 2004, 21 (1) : 40 –43. |
| [13] |
郑运虎, 姜峰. 浅海域隔水导管在风波流联合作用下的屈曲仿真[J].
西华大学学报:自然科学版, 2015, 34 (2) : 103 –107.
Zheng Yunhu, Jiang Feng. The buckling simulation of drilling riser in shallow waters under the combined effects of wind, waves and currents[J]. Journal of Xihua University:Natural Science, 2015, 34 (2) : 103 –107. |
| [14] |
姜伟. 深水钻井导管挠曲方程及固有频率研究[J].
中国海上油气, 2011, 23 (3) : 179 –184.
Jiang Wei. Calculation and study on the flexure equation and natural frequency of deepwater drilling riser[J]. China Offshore Oil and Gas, 2011, 23 (3) : 179 –184. |
| [15] |
张义民, 张守元, 李鹤, 等. 运行模态分析中固有模态和谐波模态区分方法研究[J].
振动与冲击, 2009, 28 (1) : 64 –67.
Zhang Yimin, Zhang Shouyuan, Li He, et al. Modes in operational modal analysis[J]. Journal of Vibration and Shock, 2009, 28 (1) : 64 –67. |
| [16] |
陈然, 曹咏弘, 孙华东. 基于ANSYS的内燃机曲轴的模态分析[J].
煤炭工程, 2015, 47 (4) : 108 –109, 113.
Chen Ran, Cao Yonghong, Sun Huadong. Modal analysis of engine crankshaft based on ANSYS[J]. Coal Engineering, 2015, 47 (4) : 108 –109, 113. |
| [17] |
刘建瑞, 陈斌, 张金凤, 等. 余热排出泵水中模态分析[J].
排灌机械工程学报, 2015, 33 (4) : 290 –295.
Liu Jianrui, Chen Bin, Zhang Jinfeng, et al. Mode analysis for rotor of residual heat removal pump in water[J]. Journal of Drainage and Irrigation Machinery Engineering, 2015, 33 (4) : 290 –295. |
| [18] |
廖明夫, 丛佩红, 王娟, 等. 航空发动机转子振动的热模态和减振设计[J].
航空动力学报, 2015, 30 (5) : 1125 –1140.
Liao Mingfu, Cong Peihong, Wang Juan, et al. "Hot modes" of rotor vibrations and vibration reduction design for aero-engines[J]. Journal of Aerospace Power, 2015, 30 (5) : 1125 –1140. |
| [19] |
金国光, 魏展, 秦凯旋, 等. 高速凸轮机构动力学分析及模特截断[J].
机械工程学报, 2015, 51 (13) : 227 –234.
Jin Guoguang, Wei Zhan, Qin Kaixuan, et al. Dynamic analysis and modal truncation of high-speed cam mechanism[J]. Journal of Mechanical Engineering, 2015, 51 (13) : 227 –234. DOI:10.3901/JME.2015.13.227 |
| [20] | 张宾, 唐湛棋, 孙姣, 等. 旋转圆柱绕流的动力模态分析[J]. 河北工业大学学报, 2015, 32 (6) : 145 –151. |
 2015, Vol. 37
2015, Vol. 37


