在石油勘探开发中,各式各样的管柱例如钻杆、套管、油管等得到了广泛的应用。这些管柱都工作在一个狭长的井眼内,同时承受拉、压、弯、扭、井壁约束、液体压力以及管柱接头等一系列因素影响,致使管柱力学分析变得异常复杂。经典的管柱屈曲分析中,通常忽略接头作用,将管柱看作均匀细杆并且假设管柱与井壁连续接触,在此基础上分析轴向力、扭矩等对管柱屈曲的影响。Lubinski A等利用能量方法研究了无重油管的螺旋屈曲问题,推导出了轴向力和管柱变形螺距之间的关系式[1]。Paslay P R等利用能量方法研究了斜直井眼中的正弦屈曲问题,推导出了正弦屈曲的临界载荷[2]。Mitchell R F、高德利、李子丰、刘凤梧、高宝奎、高国华等从管柱力学基本方程出发,推导了管柱屈曲微分方程,通过求解得到了管柱正弦屈曲和螺旋屈曲的解[3-20]。实际上,接头的外径一般要大于管柱的外径,导致部分管柱和井壁脱离接触,即管柱和井壁连续接触的假设不是严格成立。Mitchell R F认为接头的作用不可忽略,将受压管柱与井壁的接触情况分成3类:无接触、点接触和连续接触,但仅分析了无接触情形下管柱的正弦屈曲和螺旋屈曲[21-22]。Mitchell R F[3]、刘凤梧等[23]研究了封隔器对管柱屈曲的影响。本文基于前人的研究基础上,建立了带接头管柱的纵横弯曲模型,分别就无接触、点接触和连续接触3种情形给出管柱变形的解。
1 模型描述Lubinski A在研究受井眼约束的无重管柱的屈曲行为时,认为管柱和井壁连续接触,管柱的变形曲线为一螺旋线[1]。实际上接头的存在必然导致一部分管柱和井壁脱离接触,根据管柱和井壁的接触情况分成3类:无接触、点接触和连续接触,如图 1所示。当轴向力较小时,接头之间的管柱与井壁无接触;随着轴向力的增大,管柱径向位移增大,直至管柱上的某一点和井壁发生接触,即点接触;轴向力进一步增大将会导致部分管柱和井壁连续接触。
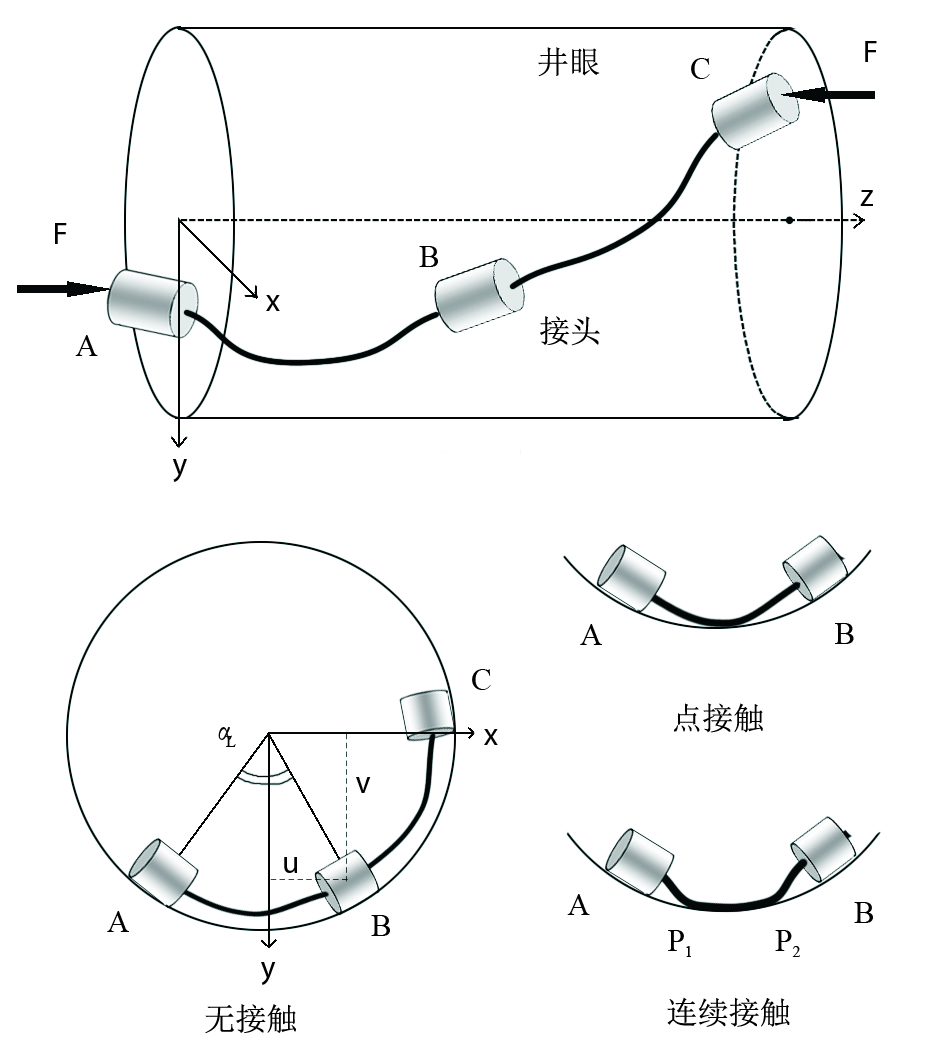 |
| 图1 管柱和井壁的接触状态 Fig. 1 Contact states between the tubular string and wellbore |
本文基于以下假设研究这3种接触情形:
(1) 井筒轴线为直线,井筒内壁看作规则圆柱体的壁面;
(2) 接头的长度相对于管柱长度忽略不计,接头外径大于管柱外径但小于井筒内径,接头与井壁之间视为点接触;
(3) 所有接头尺寸一致,接头之间的管柱几何和物理参数相同;
(4) 忽略管柱的重力、摩阻、扭矩的作用;
(5) 管柱上只存在小应变,线弹性理论成立。
2 无接触情形考虑到以上假设条件,此时管柱变形方程为[7]:
| $\left\{ {\begin{array}{*{20}{c}} {\frac{{{{\rm{d}}^4}u}}{{{\rm{d}}{z^4}}} + {k^2}\frac{{{{\rm{d}}^2}u}}{{{\rm{d}}{z^2}}} = 0}\\ {\frac{{{{\rm{d}}^4}v}}{{{\rm{d}}{z^4}}} + {k^2}\frac{{{{\rm{d}}^2}v}}{{{\rm{d}}{z^2}}} = 0} \end{array}} \right.$ | (1) |
式中:
方程(1)的通解为
| $\left\{ {\begin{array}{*{20}{c}} {u = {c_1}\cos \left( {kz} \right){r_{\rm{c}}} + {c_2}\sin (kz){r_{\rm{c}}} + {c_3}\frac{z}{L}{r_{\rm{c}}} + {c_4}{r_{\rm{c}}}}\\ {v = {c_5}\cos \left( {kz} \right){r_{\rm{c}}} + {c_6}\sin (kz){r_{\rm{c}}} + {c_7}\frac{z}{L}{r_{\rm{c}}} + {c_8}{r_{\rm{c}}}} \end{array}} \right.$ | (2) |
式中:
设相邻接头A和B的角度差为
| $\left\{ {\begin{array}{*{20}{l}} {u\left( { - \frac{L}{2}} \right) = - {r_{\rm{c}}}\sin \frac{{{\alpha _{\rm{L}}}}}{2}}\\ {v\left( { - \frac{L}{2}} \right) = {r_{\rm{c}}}\cos \frac{{{\alpha _{\rm{L}}}}}{2}}\\ {u\left( {\frac{L}{2}} \right) = {r_{\rm{c}}}\sin \frac{{{\alpha _{\rm{L}}}}}{2}}\\ {v\left( {\frac{L}{2}} \right) = {r_{\rm{c}}}\cos \frac{{{\alpha _{\rm{L}}}}}{2}} \end{array}} \right.$ | (3) |
进一步假定接头A和B之间管柱的变形曲线和接头B和C之间管柱变形曲线的空间几何形状相同,两条变形曲线之间存在角度为
| $\left[ {\begin{array}{*{20}{c}} {\frac{{\rm{d}}}{{{\rm{d}}z}}u\left( { - \frac{L}{2}} \right)}\\ { - \frac{{\rm{d}}}{{{\rm{d}}z}}v\left( { - \frac{L}{2}} \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos {\alpha _{\rm{L}}}}&{\sin {\alpha _{\rm{L}}}}\\ { - \sin {\alpha _{\rm{L}}}}&{\cos {\alpha _{\rm{L}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\frac{{\rm{d}}}{{{\rm{d}}z}}u\left( {\frac{L}{2}} \right)}\\ { - \frac{{\rm{d}}}{{{\rm{d}}z}}v\left( {\frac{L}{2}} \right)} \end{array}} \right]$ | (4) |
| $\left[ {\begin{array}{*{20}{c}} {\frac{{{{\rm{d}}^2}}}{{{\rm{d}}{z^2}}}u\left( { - \frac{L}{2}} \right)}\\ { - \frac{{{{\rm{d}}^2}}}{{{\rm{d}}{z^2}}}v\left( { - \frac{L}{2}} \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos {\alpha _{\rm{L}}}}&{\sin {\alpha _{\rm{L}}}}\\ { - \sin {\alpha _{\rm{L}}}}&{\cos {\alpha _{\rm{L}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\frac{{{{\rm{d}}^2}}}{{{\rm{d}}{z^2}}}u\left( {\frac{L}{2}} \right)}\\ { - \frac{{{{\rm{d}}^2}}}{{{\rm{d}}{z^2}}}v\left( {\frac{L}{2}} \right)} \end{array}} \right]$ | (5) |
式(4)和式(5)分别代表变形曲线一阶导数和二阶导数的变换关系,式(3)代表横向位移的变换关系。
将式(2)代入到式(3)~(5)中,得到8个包含待定常数
上面的计算中,
| ${\alpha _{\rm{L}}} = \sqrt {\frac{F}{{2{E_{\rm{I}}}}}} L = \frac{{kL}}{{\sqrt 2 }} = \frac{\varphi }{{\sqrt 2 }}$ | (6) |
其中,
| $\left\{ {\begin{array}{*{20}{l}} {{c_1} = {c_4} = {c_6} = {c_7} = 0}\\ {{c_2} = \frac{{2\left( { - 1 + \cos \frac{\varphi }{{\sqrt 2 }}} \right)\cos \frac{\varphi }{2}\sin \frac{\varphi }{{2\sqrt 2 }}}}{{\left( { - 1 + \cos \frac{\varphi }{{\sqrt 2 }}} \right)\sin \varphi - \varphi \left( { - \cos \varphi + \cos \frac{\varphi }{{\sqrt 2 }}} \right)}}}\\ {{c_3} = - 2{c_2}\sin \frac{\varphi }{2} + 2\sin \frac{\varphi }{{2\sqrt 2 }}}\\ {{c_5} = \frac{{\tan \frac{\varphi }{2}\left( {1 + \cos \frac{\varphi }{{\sqrt 2 }}} \right)}}{{\sin \frac{\varphi }{{\sqrt 2 }}}}{c_2}}\\ {{c_8} = - {c_5}\cos \frac{\varphi }{2} + \cos \frac{\varphi }{{2\sqrt 2 }}} \end{array}} \right.$ | (7) |
同时,也可以利用柱坐标系下的径向位移
| $\left\{ {\begin{array}{*{20}{l}} {r = \sqrt {{u^2} + {v^2}} }\\ {\alpha = \arctan \left( {\frac{u}{v}} \right)} \end{array}} \right.$ | (8) |
管柱产生变形后,最大径向位移位于管柱的中点,因此管柱和井壁开始接触的条件为
| $r\left( 0 \right) = {r_{\rm{p}}}$ | (9) |
式中:
将管柱变形曲线代入式(9),可得到无接触阶段结束和点接触阶段开始的临界参数,即
当管柱的中点接触井壁后,开始进入点接触阶段。此时接头之间的管柱以接触点为界分成两段,分别写出这两段管柱变形曲线的一般表达式
| $\left\{ {\begin{array}{*{20}{l}} {{u_1} = {c_1}\cos \left( {kz} \right){r_c} + {c_2}\sin \left( {kz} \right){r_c} + {c_3}\frac{z}{L}{r_c} + {c_4}{r_c}}\\ {{\upsilon _2} = {c_5}\cos \left( {kz} \right){r_c} + {c_6}\sin \left( {kz} \right){r_c} + {c_7}\frac{z}{L}{r_c} + {c_8}{r_c}} \end{array}} \right. - \frac{L}{2} \le z \le 0$ | (10) |
| $\left\{ {\begin{array}{*{20}{l}} {{u_{\rm{r}}} = {c_9}\cos \left( {kz} \right){r_{\rm{c}}} + {c_{10}}\sin (kz){r_{\rm{c}}} + {c_{11}}\frac{z}{L}{r_{\rm{c}}} + {c_{12}}{r_{\rm{c}}}}\\ {{v_{\rm{r}}} = {c_{13}}\cos \left( {kz} \right){r_{\rm{c}}} + {c_{14}}\sin (kz){r_{\rm{c}}} + {c_{15}}\frac{z}{L}r + {c_{16}}r} \end{array}} \right.0 \le z \le \frac{L}{2}$ | (11) |
其中,式(10)代表左边一段管柱的变形曲线,式(11)代表右边一段管柱的变形曲线。
根据管柱变形曲线的对称性,管柱中间接触点的角度为0,则接触点的横向位移为
| $\left\{ {\begin{array}{*{20}{l}} {{u_{\rm{l}}}\left( 0 \right) = {u_{\rm{r}}}\left( 0 \right) = 0}\\ {{v_{\rm{l}}}\left( 0 \right) = {v_{\rm{r}}}\left( 0 \right) = {r_{\rm{p}}}} \end{array}} \right.$ | (12) |
在接触点位置,管柱变形曲线的导数和二阶导数是连续的,即
| $\left\{ {\begin{array}{*{20}{l}} {\frac{{\rm{d}}}{{{\rm{d}}z}}{u_{\rm{l}}}\left( 0 \right) = \frac{{\rm{d}}}{{{\rm{d}}z}}{u_{\rm{r}}}\left( 0 \right)}\\ {\frac{{\rm{d}}}{{{\rm{d}}z}}{v_{\rm{l}}}\left( 0 \right) = \frac{{\rm{d}}}{{{\rm{d}}z}}{v_{\rm{r}}}\left( 0 \right)} \end{array}} \right.$ | (13) |
| $\left\{ {\begin{array}{*{20}{l}} {\frac{{{{\rm{d}}^2}}}{{{\rm{d}}{z^2}}}{u_{\rm{l}}}\left( 0 \right) = \frac{{{{\rm{d}}^2}}}{{{\rm{d}}{z^2}}}{u_{\rm{r}}}\left( 0 \right)}\\ {\frac{{{{\rm{d}}^2}}}{{{\rm{d}}{z^2}}}{v_{\rm{l}}}\left( 0 \right) = \frac{{{{\rm{d}}^2}}}{{{\rm{d}}{z^2}}}{v_{\rm{r}}}\left( 0 \right)} \end{array}} \right.$ | (14) |
将式(10)、式(11)代入式(3)~式(5)和式(12)~ 式(14)中,可得到16个关于待定系数
引入无因次参数
| $\left\{ {\begin{array}{*{20}{l}} {{c_1} = {c_4} = 0}\\ {{c_3} = - 2{c_2}\sin \frac{\varphi }{2} + 2\sin \frac{\varphi }{{2\sqrt 2 }}}\\ {{c_5} = \frac{{\left( {\frac{\varphi }{2} - \sin \frac{\varphi }{2}} \right){c_6} + \lambda - \cos \frac{\varphi }{{2\sqrt 2 }}}}{{1 - \cos \frac{\varphi }{2}}}}\\ {{c_7} = - \varphi {c_6}}\\ {{c_8} = \lambda - {c_5}} \end{array}} \right.$ | (15) |
其中
| $\left[ {\begin{array}{*{20}{c}} {\frac{{\sin \frac{\varphi }{2}\left( {1 + \cos \frac{\varphi }{{\sqrt 2 }}} \right)}}{{\sin \frac{\varphi }{{\sqrt 2 }}}}}&{\frac{{\left( {\varphi \cos \frac{\varphi }{2} - 2\sin \frac{\varphi }{2}} \right)}}{{2\left( { - 1 + \cos \frac{\varphi }{2}} \right)}}}\\ {\frac{{\left( {\varphi \cos \frac{\varphi }{2} - 2\sin \frac{\varphi }{2}} \right)}}{{1 + \cos \frac{\varphi }{{\sqrt 2 }}}}}&{\frac{{\varphi \left( { - \varphi - \varphi \cos \frac{\varphi }{2} + 4\sin \frac{\varphi }{2}} \right)}}{{2\sin \frac{\varphi }{2}\sin \frac{\varphi }{{\sqrt 2 }}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{c_2}}\\ {{c_6}} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {\cos \frac{\varphi }{2}\left( {\lambda - \cos \frac{\varphi }{{2\sqrt 2 }}} \right)}\\ {\frac{{\varphi \sin \frac{\varphi }{2}\left( {\lambda - \cos \frac{\varphi }{{2\sqrt 2 }}} \right)}}{{\left( {1 - \cos \frac{\varphi }{2}} \right)\sin \frac{\varphi }{{\sqrt 2 }}}} - \frac{{2\sin \frac{\varphi }{{2\sqrt 2 }}}}{{1 + \cos \frac{\varphi }{{\sqrt 2 }}}}} \end{array}} \right]$ | (16) |
后8个待定系数
| $\left\{ {\begin{array}{*{20}{l}} {{c_9} = 0}\\ {{c_{10}} = {c_2}}\\ {{c_{10}} = {c_2}}\\ {{c_{11}} = {c_3}}\\ {{c_{12}} = 0}\\ {{c_{13}} = {c_5}}\\ {{c_{14}} = - {c_6}}\\ {{c_{15}} = - {c_7}}\\ {{c_{16}} = {c_8}} \end{array}} \right.$ | (17) |
对于点接触情形而言,管柱变形曲线的最大径向位移出现在管柱的中点,其余点的径向位移都小于中点的位移;当进入连续接触阶段后,管柱变形最大径向位移发生在中点附近的一段管柱上,故点接触阶段结束、连续接触阶段开始的临界条件为
| ${{\rm{d}}^2}r\left( 0 \right){\rm{d}}{z^2} = 0$ | (18) |
将管柱变形曲线代入式(18),即可以得到临界参数,即
当管柱中间部分P1—P2接触井壁时,进入了连续接触阶段。同时对连续接触段P1—P2和悬空段A—P1和P2—B进行研究,将会导致复杂的运算。这里介绍一种简化方法,将连续接触的情形近似等效为点接触的情形,然后利用前面点接触的求解方法来得到连续接触的解。
首先考察悬空段,图 2中管柱悬空段A—P1和点接触情形下左边一段管柱A'—M是相似的,并且在P1和M点处都满足式(18);同理,管柱P2—B和M—B'也是类似的。因此,可以将A—P1和P2—B近似等效为管柱A'—B'变形问题,即管柱A—B连续接触问题近似等效为管柱A'—B'刚好达到点接触到连续接触临界条件。
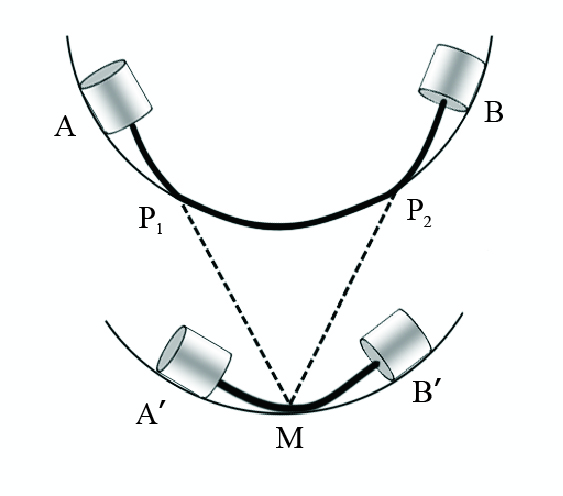 |
| 图2 连续接触情形的简化 Fig. 2 Simplification of the wrap contact |
假设连续接触管柱长度为
| ${\varphi _{\rm{c}}} = k\left( {L - {L_{\rm{c}}}} \right) = \varphi \left( {1 - \frac{{{L_{\rm{c}}}}}{L}} \right)$ | (19) |
用
对于连续接触段,利用一段螺旋曲线来描述
| $\left\{ \begin{array}{l} u = {r_{\rm{p}}}\sin \beta z \\ v = {r_{\rm{p}}}\cos \beta z \\ \end{array} \right.$ | (20) |
其中,
| $\beta = \frac{{{\rm{d}}\alpha \left( { - \frac{{{L_{\rm{c}}}}}{2}} \right)}}{{{\rm{d}}z}}$ | (21) |
通过以上的近似处理,可以得到连续接触情形下管柱的变形曲线。经验证,管柱变形的横向位移、位移的一阶、二阶导数在连接点P1和P2处是连续的,但是位移的三阶导数在连接点处是不连续的。说明上述近似方法在连接点处的弯矩是连续的,而剪力是不连续的,对于工程问题而言精度是足够的。
5 计算结果分析根据式(9)和式(18)得到了无接触到点接触和点接触到连续接触的临界值,结果如图 3所示。
| $\left\{ \begin{array}{l} {F_{{\rm{np}}}} = EI{\left( {\dfrac{{3.48}}{L}} \right)^2} \\ {F_{{\rm{pw}}}} = EI{\left( {\dfrac{{5.90}}{L}} \right)^2} \\ \end{array} \right.$ | (22) |
式中:
在经典的压杆稳定问题中,当杆的两端是铰支约束时,屈曲的临界条件约为
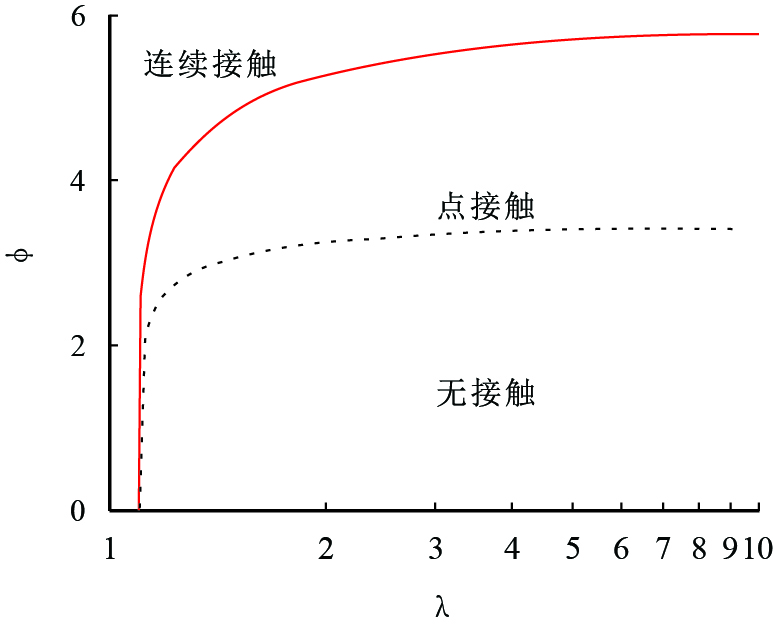 |
| 图3 接触情形的分类 Fig. 3 Three contact cases |
以
点接触阶段(
当轴向力比较小时(例如
点接触阶段(
当达到了无接触到点接触的临界条件(
连续接触阶段(
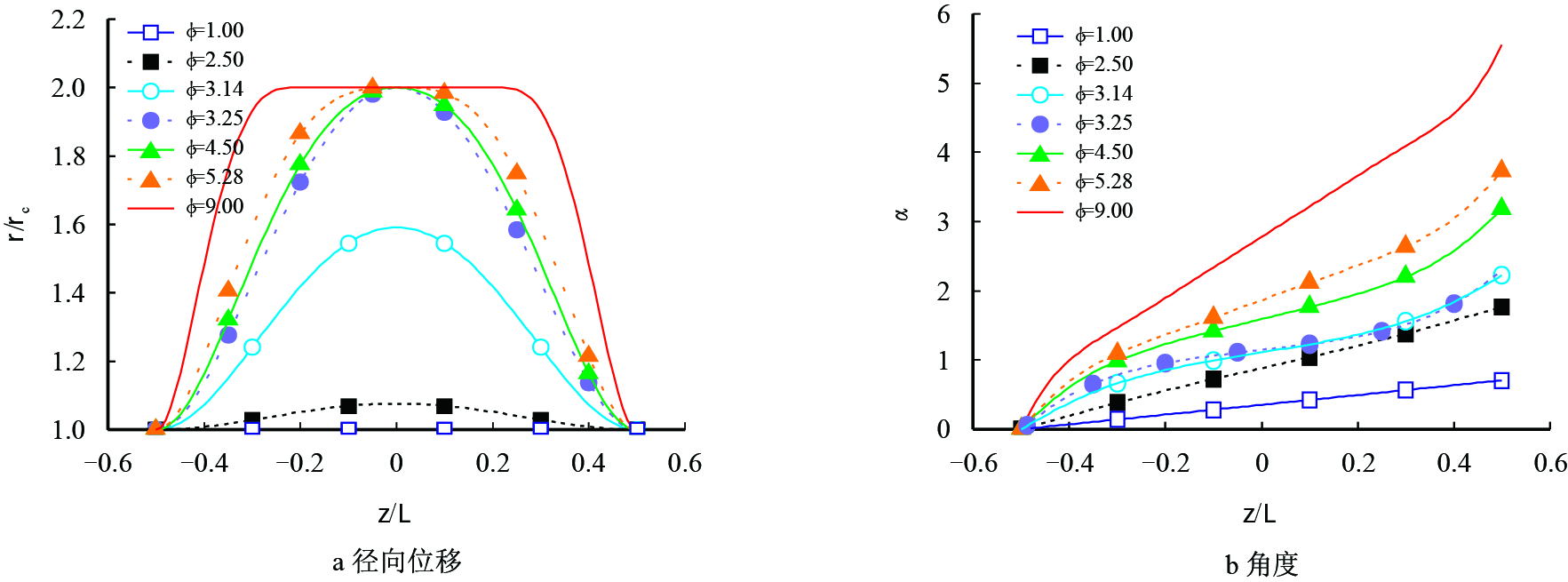 |
| 图4 管柱的变形曲线 Fig. 4 Deflection curves of the tubular string |
达到点接触到连续接触的临界条件(
本文提出的模型完整地描述了带接头管柱纵横弯曲的3种状态:无接触、点接触和连续接触。当井筒、接头和管柱相关参数以及管柱两端轴向力给定后,利用本文模型可以求得管柱弯曲状态以及变形曲线。计算结果表明,管柱视半径与接头视半径之比(
| [1] | Lubinski A, Althouse W S. Helical buckling of tubing sealed in packers[J]. Journal of Petroleum Technology, 1962, 14 (6) : 655 –670. DOI:10.2118/178-PA |
| [2] | Paslay P R, Bogy D B. The stability of a circular rod laterally constrained to be in contact with an inclined circular cylinder[J]. Journal of Applied Mechanics, 1964, 31 (4) : 605 –610. DOI:10.1115/1.3629721 |
| [3] | Mitchell R F. New concepts for helical buckling[J]. SPE Drilling Engineering, 1988, 3 (3) : 303 –310. DOI:10.2118/15470-PA |
| [4] | Mitchell R F. Effects of well deviation on helical buckling[J]. SPE Drilling & Completion, 1997, 12 (1) : 63 –70. |
| [5] | Robert F M. A buckling criterion for constant-curvature wellbores[J]. SPE Journal, 1999, 4 (4) : 349 –352. DOI:10.2118/57896-PA |
| [6] | 高德利. 油气井管柱力学与工程[M]. 东营: 中国石油大学出版社, 2006 . |
| [7] | 高德利. 井眼轨迹控制[M]. 东营: 中国石油大学出版社, 1994 . |
| [8] |
高德利, 高宝奎. 水平井段管柱屈曲与摩阻分析[J].
石油大学学报:自然科学版, 2000, 24 (2) : 1 –3.
Gao Deli, Gao Baokui. Effects of tubular buckling on torque and drag in horizontal well[J]. Journal of China University of Petroleum, China, 2000, 24 (2) : 1 –3. |
| [9] |
高德利, 刘凤梧, 徐秉业. 弯曲井眼中管柱屈曲行为研究[J].
石油钻采工艺, 2000, 22 (4) : 1 –4.
Gao Deli, Liu Fengwu, Xu Bingye. Study on the buckling behavior of pipe string in crooked hole[J]. Oil Drilling & Production Technology, 2000, 22 (4) : 1 –4. |
| [10] |
高德利, 刘凤梧, 徐秉业. 油气井管柱的屈曲行为研究[J].
自然科学进展, 2001, 11 (9) : 976 –980.
Gao Deli, Liu Fengwu, Xu Bingye. Analysis of buckling behaviors of down-hole tubular strings[J]. Progress in Natural Science, 2001, 11 (9) : 976 –980. |
| [11] |
李子丰, 马兴瑞, 黄文虎. 水平管中受压扭细长圆杆(管)的线性弯曲[J].
哈尔滨工业大学学报, 1994, 26 (1) : 96 –100.
Li Zifeng, Ma Xingrui, Huang Wenhu. The buckling of a circular rod or pipe laterally constrained to be contact with a horizontal circular cylinder[J]. Journal of Harbin Institute of Technology, 1994, 26 (1) : 96 –100. |
| [12] |
李子丰, 马兴瑞, 黄文虎. 油气井杆管柱的静力稳定性[J].
工程力学, 1997, 14 (1) : 17 –25.
Li Zifeng, Ma Xingrui, Huang Wenhu. Static stability of pipe string in oil and gas wells[J]. Engineering Mechanics, 1997, 14 (1) : 17 –25. |
| [13] | 刘凤梧. 受圆管约束管柱的后屈曲行为研究[D]. 北京:清华大学, 1999. |
| [14] |
刘凤梧, 徐秉业, 高德利. 水平圆管中受压扭作用管桩屈曲后的解析解[J].
力学学报, 1999, 31 (2) : 238 –242.
Liu Fengwu, Xu Bingye, Gao Deli. An analytic solution for post-buckling of tubulars subjected to axial and torsional loading in horizontal circular cylinders[J]. Acta Mechanica Sinica, 1999, 31 (2) : 238 –242. |
| [15] |
高宝奎, 高德利. 水平井段管柱螺旋屈曲的数值计算[J].
钻采工艺, 1997, 20 (5) : 10 –11.
Gao Baokui, Gao Deli. Numerical solutions of helical buckling of tubular strings in horizontal wells[J]. Drilling & Production Technology, 1997, 20 (5) : 10 –11. |
| [16] | Gao Guohua, Miska S. Effects of friction on post-buckling behavior and axial load transfer in a horizontal well[J]. SPE Journal, 2010, 15 (4) : 1110 –1124. |
| [17] | Gao Guohua, Miska S. Effects of boundary conditions and friction on static buckling of pipe in a horizontal well[J]. SPE Journal, 2009, 14 (4) : 782 –796. DOI:10.2118/111511-PA |
| [18] |
高国华, 李琪, 李淑芳. 管柱在水平井眼中的屈曲分析[J].
石油学报, 1996, 17 (3) : 123 –130.
Gao Guohua, Li Qi, Li Shufang. A buckling analysis of pipe string in horizontal boreholes[J]. Acta Petrolei Sinica, 1996, 17 (3) : 123 –130. |
| [19] |
高国华, 李琪, 李淑芳. 弯曲井眼中受压管柱的屈曲分析[J].
应用力学学报, 1996, 13 (1) : 115 –120.
Gao Guohua, Li Qi, Li Shufang. Buckling analysis for pipe string constrained in curved boreholes[J]. Chinese Journal of Applied Mechanics, 1996, 13 (1) : 115 –120. |
| [20] |
高国华, 张福祥, 王宇, 等. 水平井眼中管柱的屈曲和分叉[J].
石油学报, 2001, 22 (1) : 95 –99.
Gao Guohua, Zhang Fuxiang, Wang Yu, et al. Buckling and bifurcation of pipes in horizontal wells[J]. Acta Petrolei Sinica, 2001, 22 (1) : 95 –99. |
| [21] | Mitchell R F. Helical buckling of pipe with connectors in vertical wells[J]. SPE Drilling & Completion, 2000, 15 (3) : 162 –166. |
| [22] | Mitchell R F. Lateral buckling of pipe with connectors in horizontal wells[J]. SPE Journal, 2003, 8 (2) : 124 –137. DOI:10.2118/84950-PA |
| [23] |
刘凤梧, 徐秉业, 高德利. 封隔器对油管螺旋屈曲的影响分析[J].
清华大学学报:自然科学版, 1999, 39 (8) : 105 –108.
Liu Fengwu, Xu Bingye, Gao Deli. Packer effect analysis of helical buckling of well tubing[J]. Journal of Tsinghua University:Science & Technology, 1999, 39 (8) : 105 –108. |
 2015, Vol. 37
2015, Vol. 37


