2013年,美国能源信息署(EIA)发布的《Technically Recoverable Shale Oil and Shale Gas Resources:An Assessment of 137 Shale Formations in 41 Countries Outside the United States》报告包含了美国在内的42个国家的页岩气资源评价成果,报告指出,全球页岩气的技术可采资源总量为220.73×1012 m3[1],显示出全球页岩气资源丰富,开采潜力大。页岩气的赋存形式不同于常规油气藏,其赋存状态包括游离态、吸附态和溶解态等[2],其中游离气主要保存在页岩储层中微裂缝和有机质或矿物颗粒间大孔中,而吸附气主要保存在页岩的矿物颗粒和有机质结构内部的微孔隙之中。Curtis J B[3]研究美国5个盆地的页岩气藏储层特征,总结了5个盆地的页岩气藏吸附气含量变化,吸附气所占比例为20%~85%,吸附气在页岩气储量中占有重要地位。因此,研究页岩吸附性能对页岩气的资源评价有重要的意义。目前,研究页岩吸附性能主要的手段是在室内开展等温吸附实验,Ross D J K等人对不同类型的页岩样品通过等温吸附实验手段研究了有机碳含量、有机质类型、有机质成熟度、黏土矿物等对页岩吸附性能的影响[4-13]。为了研究页岩储层吸附能力,常常在室内用高温条件模拟页岩储层条件展开页岩样品等温吸附实验,实验温度一般为293~363 K,然而页岩储层温度是随着储层埋深增加呈上升趋势。对于页岩等温吸附线主要采用亚临界Langmuir模型进行拟合,因为Langmuir模型比较简单且对页岩吸附数据有较好拟合效果[4-7, 9]。然而,部分研究表明未考虑吸附剂非均质性的Langmuir模型对页岩等温吸附数据拟合效果不理想,认为其不适合研究页岩吸附特性[10, 14-16]。同时,基于Langmuir模型预测的饱和吸附量是一个与温度有关的函数,即利用Langmuir模型预测页岩吸附能力需要进行不同温度的等温吸附测试[17]。
国内外学者开展了页岩的甲烷等温吸附实验,其实验温度已超过甲烷临界温度(190.56 K)[4-13],即甲烷在页岩表面上吸附行为为超临界吸附。同时,甲烷在页岩表面上吸附属于固-气物理吸附,其作用力主要是色散力(范德华力),而色散力与温度无关。根据吸附势理论可知[18],对超临界气体吸附等温实验数据处理可建立气体-吸附剂的吸附特征曲线,该特征曲线与温度无关,依据该吸附特征曲线,可预测不同温度下的等温吸附线。Amankwah K A等[19-21]研究了吸附特征曲线,但没有给出吸附特征曲线表达式;崔永君等[22-25]研究了吸附特征曲线,并通过拟合成多项式或指数形式表征吸附特征曲线,这些方法虽比较简单,但拟合的多项式或指数形式表达式参数缺乏物理意义。基于吸附势理论推导的Dubinin-Astakhov(D-A)模型在物理吸附中有较广泛的应用[16, 19-20, 26-31],其不仅适用于亚临界吸附研究,也适用于超临界吸附研究[27]。因此,在前人研究的基础上,引入过剩吸附量,对吸附实验中的吸附气量进行修正,并对D-A方程进行改进,将改进后的方程应用于页岩中超临界甲烷的吸附特征曲线的研究。对页岩中超临界甲烷吸附等温实验数据进行非线性拟合,对虚拟饱和蒸汽压的计算方法进行优选,得到适合超临界甲烷在页岩中吸附研究的最优计算方法和页岩最优吸附特征曲线。同时,对页岩中超临界甲烷吸附等温实验数据进行非线性拟合,得到与温度无关的页岩吸附特征曲线,该特征曲线可反映页岩的吸附特征。
1 等温吸附实验数据以美国的4组富含有机质页岩样品为研究对象,包括Utah盆地Green River地层页岩(
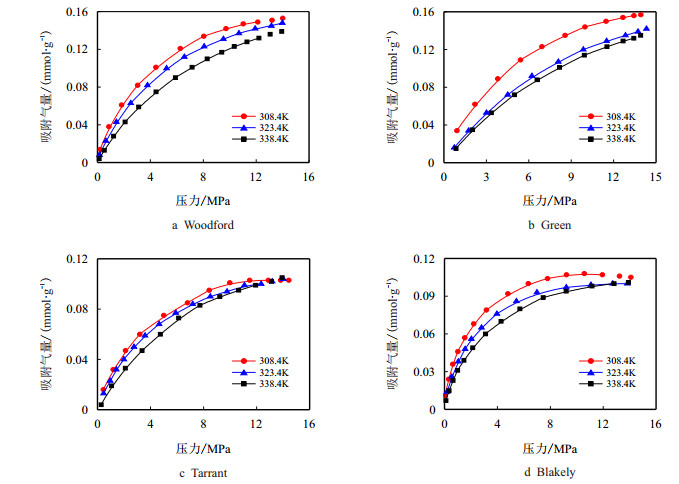 |
| 图1 页岩吸附甲烷的等温线 Fig. 1 CH4 adsorption isotherms for shale at different temperatures |
甲烷在页岩储层中的吸附既属于物理吸附,又属于超临界吸附。引入过剩吸附量,对吸附实验中的吸附气量进行修正,并对D-A方程进行改进,%将改进后的方程应用于研究页岩中超临界甲烷的吸附研究。
根据Gibbs定义,吸附实验测得吸附量为过剩吸附量,而理论吸附量为绝对吸附量,两者关系为
| $ {n_{{\rm{ad}}}} = n{\left( {1-{\rho _{\rm{g}}}/{\rho _{{\rm{ad}}}}} \right)^{-1}} $ | (1) |
式(1)中,在实验温度、压力下的气相密度
| 表1 甲烷密度回归公式系数取值 Table 1 Coefficient values of regressive equation of methane density |
| $ {\rho _{\rm{g}}} = {c_0} + {c_1}p + {c_2}{p^2} + {c_3}{p^3} $ | (2) |
利用公式(1)对页岩中超临界甲烷等温吸附数据进行处理时,处于超临界状态下甲烷的吸附相密度是不能直接测量或是直接计算,其值是一个近似值[32]。目前,国内外学者提出了多种吸附相密度的经验公式[16, 28,33],本文采用Ozawa S等提出的吸附相密度经验公式的计算[28]。吸附相密度的Ozawa经验公式为
| $ {\rho _{{\rm{ad}}}} = {\rho _{\rm{b}}}{{\rm{e}}^{-0.0025 \times \left( {T-{T_{\rm{b}}}} \right)}} $ | (3) |
基于吸附势理论,Dubinin和Radushkevich提出微孔体积填充模型,即Dubinin-Radushkevich模型[34],该模型的拟合效果不理想,因此,Dubinin和Astakhov对该模型进行改进,提出适用范围更广的最优化微孔体积填充模型,即Dubinin-Astakhov模型[26],对D-A方程进行改进,其方程表达式为
| $ V{\rm{ = }}{V_{\rm{o}}}{{\rm{e}}^{-{{\left( {A{\rm{ }}/AE} \right)}^t}}} $ | (4) |
| $ V{\rm{ = }}\left( {{n_{{\rm{ad}}}} \times {{10}^{ - 3}} \times M} \right)/{\rho _{{\rm{ad}}}} $ | (5) |
| $ A{\rm{ = R}}T\ln \frac{{{p^{\rm{o}}}}}{p} $ | (6) |
利用式(5)计算吸附势时,需要确定某个温度下的饱和蒸汽压,而在超临界条件下,饱和蒸汽压就失去了相应的物理意义。目前国内外许多学者提出采用虚拟饱和蒸汽压的概念代替饱和蒸汽压,并提出了多个经验公式[19-20, 26-27, 33-35]。计算虚拟饱和蒸汽压的经验公式有
| $ {p^{\rm{o}}} = {p_{\rm{c}}}{\left( {\frac{T}{{{T_{\rm{c}}}}}} \right)^2} $ | (7) |
| $ {p^{\rm{o}}} = {p_{\rm{c}}}{{\rm{e}}^{\left[ {\frac{{{T_{\rm{b}}}}}{{{T_{\rm{c}}}}} \cdot \frac{{\ln {p_{\rm{c}}}}}{{1 - {T_{\rm{b}}}/{T_{\rm{c}}}}} \cdot \left( {1 - \frac{{{T_{\rm{c}}}}}{T}} \right)} \right]}}$ | (8) |
(3) Antoine方程外推法[27]
| $ \ln {p^{\rm{o}}} = B-C/\left( {D + T} \right) $ | (9) |
Antoine方程为一个最简单的3参数蒸汽压方程,利用甲烷临界温度下饱和蒸汽压实验数据进行非线性回归可得到Antoine方程参数,将Antoine方程外推到甲烷临界温度上。利用NIST网上化学数据库提供在温度100~190 K甲烷饱和蒸汽压数据[36],对其进行非线性回归,得到甲烷Antoine方程参数为B=7.744、C=1306.549、D=19.436,同时将Antoine方程外推到甲烷临界温度上,计算超临界甲烷的虚拟饱和蒸汽压。
(4) Astakhov法[26]
| $ \ln {p^{\rm{o}}} = a/T + b $ | (10) |
参数a、b由气体的临界点(
(5) Amankwah法[19]
Amankwah法计算虚拟饱和蒸汽压公式为
| $ {p^{\rm{o}}} = {p_{\rm{c}}}{\left( {\frac{T}{{{T_{\rm{c}}}}}} \right)^k} $ | (11) |
根据吸附势理论,对于特定的吸附体系(甲烷-页岩体系),任意温度及压力下吸附相体积V与吸附势A的关系可被表达为单一的吸附特征曲线。利用D-A方程的改进式(式(4))对页岩中超临界甲烷等温吸附数据得到吸附相体积和吸附势,通过非线性拟合得到吸附特征曲线的参数,建立页岩吸附特征曲线。相关系数是评价拟合好坏的一个标准,利用5种虚拟饱和蒸汽压计算方法的拟合相关系数来判断其拟合效果,优选出适合超临界甲烷在页岩中吸附研究的最优虚拟饱和蒸汽压计算方法。
3.1 Dubinin法页岩吸附相体积利用式(1)计算,吸附势利用式(6)计算,虚拟饱和蒸汽压采用Dubinin法(式(7))计算。基于Dubinin法的特征曲线参数见表 2,基于Dubinin法页岩3个温度的吸附相体积和吸附势的关系见图 2。从图 2中可看出,部分吸附势小于零,主要是因为基于Dubinin法计算的虚拟饱和蒸汽压偏低,温度308.4 K的虚拟饱和蒸汽压为12.046 MPa,温度323.4 K的虚拟饱和蒸汽压为13.246 MPa,温度为338.4 K的虚拟饱和蒸汽压为14.504 MPa,这说明Dubinin法对于较高压力的超临界甲烷吸附存在局限性,比较适合压力较低超临界甲烷吸附。采用D-A模型(式(4))对图 2中吸附相体积和吸附势数据点(排除小于零的数据点)进行非线性拟合,得到D-A方程改进式中的参数(Vo,E,t)。基于Dubinin法的特征曲线拟合结果见图 3,从图 3中可见,页岩吸附相体积和吸附势数据点都几乎落在同一条曲线上,说明页岩吸附特征曲线和温度无关。可见,基于Dubinin法的拟合页岩特征曲线具有较高的拟合精度,其中Woodford页岩相关系数最大为0.9984,Tarrant页岩的相关系数最小为0.9881。Dubinin法计算的虚拟饱和蒸汽压偏低,不适合用于压力较高的页岩中超临界甲烷吸附特征曲线研究。
| 表2 Dubinin法拟合的吸附特征曲线 Table 2 Regression parameters for the characteristic curve using the Dubinin method |
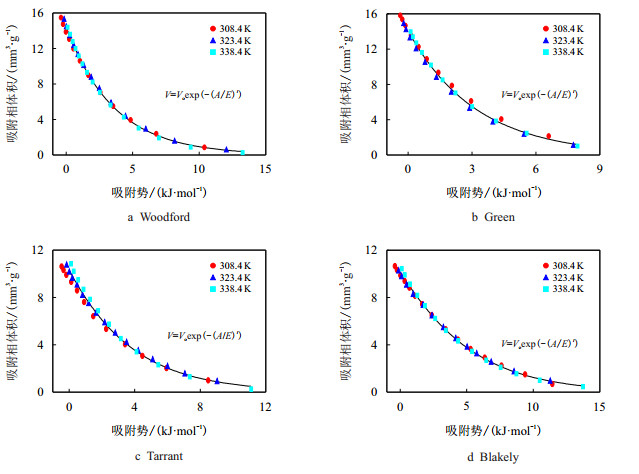 |
| 图2 Dubinin法拟合的吸附特征曲线 Fig. 2 Characteristic curves for shale samples using the Dubinin method |
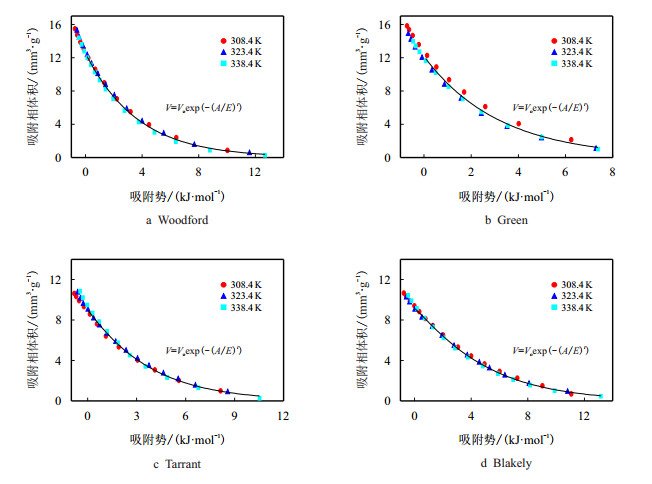 |
| 图3 Reid法拟合的吸附特征曲线 Fig. 3 Characteristic curves for shale samples using the Reid method |
基于Reid法页岩的吸附相体积和吸附势的关系见图 3,可以看出,部分吸附势小于零,主要是因为基于Reid法计算的虚拟饱和蒸汽压偏低,温度308.4 K的虚拟饱和蒸汽压为10.498 MPa,温度323.4 K的虚拟饱和蒸汽压为11.168 MPa,温度为338.4 K的虚拟饱和蒸汽压为11.817 MPa,这也说明Reid法对于较高压力的超临界甲烷吸附存在局限性,较适合压力较低的超临界甲烷吸附。
基于Reid法拟合的吸附特征曲线参数见表 3,可见,基于Reid法的拟合页岩特征曲线具有较高拟合精度,其中Blakely页岩的相关系数最大为0.9979,Green页岩的相关系数最小为0.9825。Reid法计算的虚拟饱和蒸汽压偏低,不适合用于压力较高的页岩中超临界甲烷吸附特征曲线研究。
| 表3 Reid法的吸附特征曲线参数 Table 3 Regression parameters for the characteristic curve using the Reid method |
基于Antoine方程外推法页岩的吸附相体积和吸附势的关系见图 4,从图中可看出基于该方法计算的吸附势偏大,导致不同温度的吸附相体积和吸附势数据点较分散,可能是因为基于Antoine方程外推法计算的虚拟饱和蒸汽压偏高,温度308.4 K的虚拟饱和蒸汽压为42.877 MPa,温度323.4 K的虚拟饱和蒸汽压为51.045 MPa,温度为338.4 K的虚拟饱和蒸汽压为59.887 MPa。
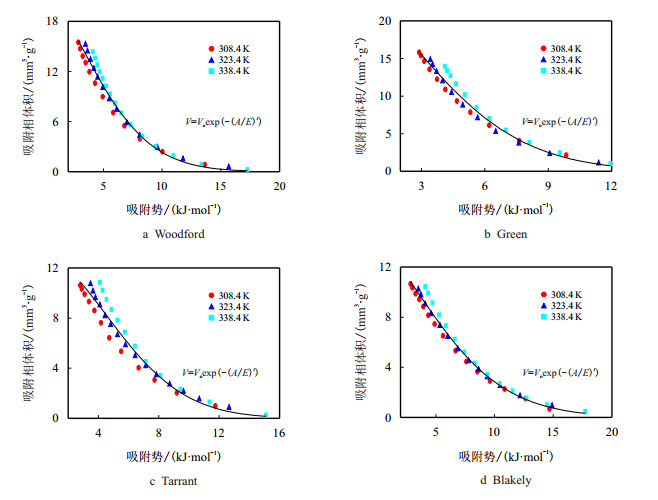 |
| 图4 Antoine方程外推法拟合的吸附特征曲线 Fig. 4 Characteristic curves for shale samples using the Antoine equation |
Antoine方程外推法拟合的吸附特征曲线参数见表 4,相关系数均低于0.9900,其中Blakely页岩的相关系数最大,为0.9825,Tarrant页岩的相关系数最小,为0.9482,可见基于Antoine方程外推法的拟合页岩特征曲线的拟合精度不太理想。Antoine方程外推法计算的虚拟饱和蒸汽压偏高,吸附势偏大,页岩吸附特征曲线的拟合效果不理想。
| 表4 Antoine方程外推法的吸附特征曲线参数 Table 4 Regression parameters for the characteristic curve using the Antoine equation |
基于Astakhov法页岩的吸附相体积和吸附势的关系见图 5,可以看出,该方法计算的吸附势偏大,不同温度的吸附相体积和吸附势数据点较分散,温度308.4 K的虚拟饱和蒸汽压为36.472 MPa,温度323.4 K的虚拟饱和蒸汽压为42.600 MPa,温度为338.4 K的虚拟饱和蒸汽压为49.078 MPa。
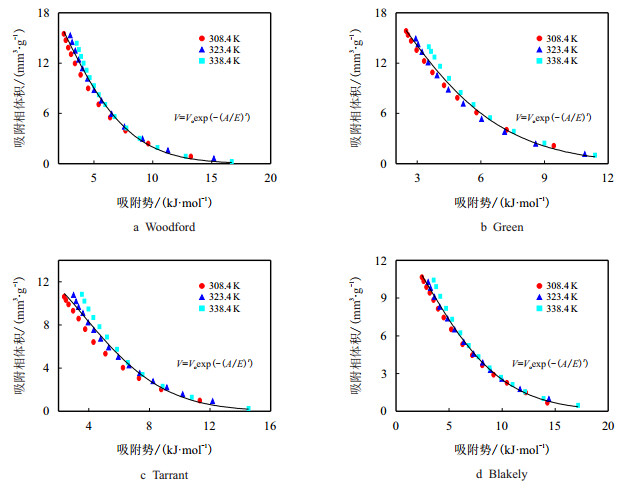 |
| 图5 Astakhov法拟合的吸附特征曲线 Fig. 5 Characteristic curves for shale samples using the Astakhov method |
Astakhov法的页岩特征曲线拟合方程外推法拟合的吸附特征曲线参数见表 5,可见Astakhov法的拟合页岩特征曲线的拟合精度不太理想,相关系数均低于0.9900,其中Blakely页岩的相关系数最大,为0.9868,Tarrant页岩的相关系数最小,为0.9573。Astakhov法计算的虚拟饱和蒸汽压偏高,基于该方法计算的吸附势偏大,%导致页岩吸附特征曲线的拟合效果不理想。
| 表5 Astakhov法的吸附特征曲线参数 Table 5 Regression parameters for the characteristic curve using the Astakhov method |
页岩吸附势中的虚拟饱和蒸汽压采用Amankwah法(式(11))计算时,需先确定系数k的值。Amankwah K A等[19]将式(12)和式(6)代入D-A吸附模型中可得到一个4参数(Vo,E,t,k)的方程,对每个温度下的等温吸附数据非线性拟合可得到每个温度下系数k的值
| $ \frac{V}{{{V_{\rm{o}}}}}{\rm{ = }}{{\rm{e}}^{- {{\left[{\frac{{{\rm{R}}T}}{E}\ln \frac{{{p_{\rm{c}}}{{\left( {T/{T_{\rm{c}}}} \right)}^k}}}{p}} \right]}^t}}} $ | (12) |
| $ V = 22.4{n_{{\rm{ad}}}} $ | (13) |
将式(12)拟合的每个温度的k值代入式(5)中,可得到每个温度下的页岩吸附势A,利用D-A方程的改进式(式(3))对吸附相体积V与吸附势A,进行非线性拟合得到页岩的吸附特征曲线,而并不能得到单一的吸附特征曲线[17, 31],同时也得到多个k值,对于一个特定的吸附体系不能得到最优的k值,说明这种方法得到的k值不合理。
在前人研究的基础上[17, 25],对Amankwah求取系数k值方法进行改进,步骤为:
(1) 假定一个系数k值,分别代入式(11)和式(5)得到虚拟饱和蒸汽压和页岩的吸附势(保证吸附势大于零);
(2) 利式(3)对吸附相体积V与吸附势A进行非线性拟合得到页岩吸附特征曲线,并得到拟合曲线的相关系数;
(3) 改变系数k值,重复步骤(1)、(2),得到一系列k值和相关系数的对应关系;
(4) 对k和相关系数进行回归得到k和相关系数的多项式,该多项式在合理范围内中相关系数极大值对应的k值为最优k值。
页岩样品的k和相关系数的多项式曲线见图 6。多项式(b0,b1,b2,b3,b4)参数见表 6。%看出每个页岩样品的k值和相关系数间拟合多项式的表达式不同且每个多项式的拟合精度高,相关系数均大于0.9999。根据前文分析,最优k值除与吸附剂有关外,还与吸附体系中的温度和压力有关,即满足计算的吸附势大于零。通过该方法得到各页岩吸附体系的最优k分别为:Woodford页岩2.3165,Green页岩2.3005,Tarrant页岩2.3758,Blakely页岩2.3262。
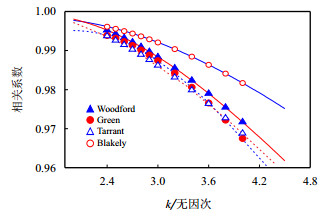 |
| 图6 k和相关系数的回归多项式曲线 Fig. 6 k and correlation coefficent curve for characteristic regression analysis |
| 表6 k和相关系数拟合的多项式参数 Table 6 Regression parameters for relationship between k and correlation coefficient |
用最优k值计算的吸附势A,其与吸附相体积V关系见图 7。用D-A方程的改进式(式(3))进行非线性拟合得到页岩的吸附特征曲线(图 7,蓝色曲线),其特征曲线参数见表 7,可见Amankwah法具有较高拟合精度,拟合效果较好,该方法可得到最优的页岩中超临界甲烷吸附特征曲线。
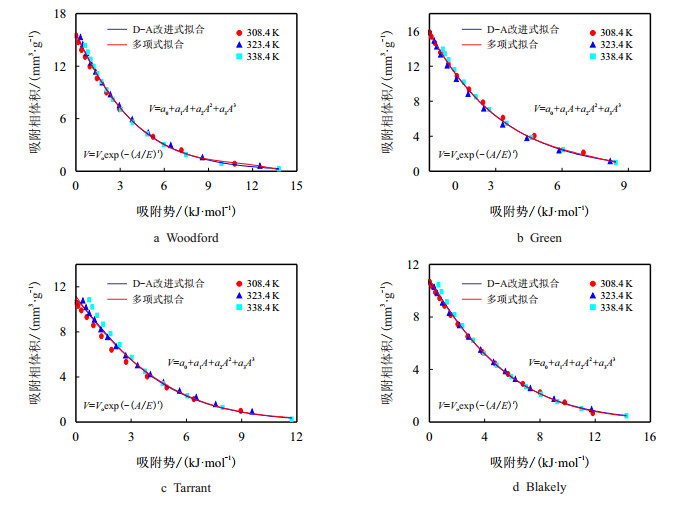 |
| 图7 Amankwah法拟合的吸附特征曲线 Fig. 7 Characteristic curves for shale samples using the Amankwah method |
| 表7 Amankwah方法的吸附特征曲线参数 Table 7 Regression parameters for the characteristic curve using the Amankwah method |
采用多项式对图 7中页岩的吸附势A和吸附相体积V数据点进行回归,可得三阶多项式定量表达的吸附特征曲线,其中多项式的表达式曲线见图 7(红色曲线),多项式的参数见表 8。其拟合相关系数与D-A方程改进式拟合相关系数相差较小,两种方法拟合的吸附特征曲线基本重合,采用多项式和D-A方程改进式都能通过拟合得到页岩中超临界甲烷的吸附特征曲线。
| 表8 多项式的吸附特征曲线参数 Table 8 Regression parameters for the characteristic curve from the polynomial curves fitting |
但采用多项式拟合的吸附特征曲线参数(a0, a1, a2, a3)没有物理意义,而采用D-A方程改进式拟合的吸附特征曲线参数(Vo, E, t)具有明确的物理意义。
从图 7中可看出,每种页岩的吸附特征曲线得到的页岩极限吸附相体积Vo只有一个,由其得到页岩极限吸附量也只有一个,而Langmuir模型得到页岩饱和吸附量是温度的函数[7];同时,页岩极限吸附相体积与TOC含量存在一定的相关性,即随着TOC含量的增加而增加。吸附特征能E是描述页岩表面与气体之间的作用力,从表 7中可看出,其与极限吸附相体积成相反的相关性,即极限吸附相体积越大,吸附特征能越小;同时,周亚平等研究认为吸附特征能与微孔孔径成反比[37],即微孔越大,吸附特征能越小,说明页岩极限吸附相体积越大,微孔半径越大,其吸附特能越小。指数t反映了吸附剂表面能量分布的不均匀性,从表 7见,其与TOC含量存在一定的关联性,即随着TOC含量的增加而呈增加的趋势;页岩中有机质、黏土矿物和非黏土矿物表面分布能量不同,有机质表面分布能量高于黏土矿物和非黏土矿物表面分布能量[13],甲烷分子将在有机质、黏土矿物与非黏土矿物表面竞争吸附,TOC含量增加,甲烷分子在有机质、黏土矿物与非黏土矿物表面吸附竞争增多,反映页岩表面能量分布非均匀性增强。
4 结语(1) 将D-A方程改进式应用于页岩中超临界甲烷吸附特征,得到了具有物理意义参数的吸附特征曲线,研究结果表明:页岩中超临界甲烷吸附特征曲线与温度无关。
(2) 页岩吸附势中的虚拟饱和蒸汽压的经验公式中,Dubinin法和Reid法计算的虚拟饱和蒸汽压偏低,Antoine方程外推法和Astakhov法计算的虚拟饱和蒸汽压偏高,而Amankwah法是计算虚拟饱和蒸汽压的最优方法,饱和蒸汽压除与吸附体系有关外,还与吸附体系的温度和压力范围有关。
| [1] | U S Energy Information Administration(EIA). Technically recoverable shale oil and shale gas resources:an assessment of 137 shale formations in 41 countries outside the United States[EB/OL]. http://www.eia.gov/analysis/studies/worldshalegas. |
| [2] |
张金川, 金之钧, 袁明生. 页岩气成藏机理和分布[J].
天然气工业, 2004, 24 (7) : 15 –18.
Zhang Jinchuan, Jin Zhijun, Yuan Mingsheng. Reservoiring mechanism of shale gas and its distribution[J]. Natural Gas Industry, 2004, 24 (7) : 15 –18. |
| [3] | Curtis J B. Fractured shale gas systems[J]. AAPG Bulletin, 2002, 86 (11) : 1921 –1938. |
| [4] | Ross D J K, Bustin R M. The importance of shalecomposition and pore structure upon gas storage potential of shale gas reservoirs[J]. Marine and Petroleum Geology, 2009, 26 (6) : 916 –927. DOI:10.1016/j.marpetgeo.2008.06.004 |
| [5] | Beaton A P, Pawlowicz J G, Anderson S D A, et al. Total organic carbon and adsorption isotherms of the duvernay and muskwa formations in alberta:shale gas data release[R]. Energy Resources Conservation Board, ERCB/AGS, Edmonton, Alberta, 2010. |
| [6] | Gasparik M, Ghanizadeh A, Bertier P, et al. Highpressure methane sorption isotherms of black shales from the Netherlands[J]. Energy & fuels, 2012, 26 (8) : 4995 –5004. |
| [7] | Zhang T, Ellis G S, Ruppel S C, et al. Effect of organicmatter type and thermal maturity on methane adsorption in shale-gas systems[J]. Organic Geochemistry, 2012, 47 : 120 –131. DOI:10.1016/j.orggeochem.2012.03.012 |
| [8] |
李武广, 杨胜来, 陈峰, 等. 温度对页岩吸附解吸的敏感性研究[J].
矿物岩石, 2012, 32 (2) : 115 –120.
Li Wuguang, Yang Shenglai, Chen Feng, et al. The sensitivity study of shale gas adsorption and desorption with rising reservoir temperature[J]. Journal of Mineralogy and Petrology, 2012, 32 (2) : 115 –120. |
| [9] |
武景淑, 于炳松, 李玉喜. 渝东南渝页1井页岩气吸附能力及其主控因素[J].
西南石油大学学报:自然科学版, 2012, 34 (4) : 40 –48.
Wu Jingshu, Yu Bingsong, Li Yuxi. Adsorption capacity of shale gas and controlling factors from the Well Yuye 1 at the southeast of Chongqing[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2012, 34 (4) : 40 –48. |
| [10] |
张志英, 杨盛波. 页岩气吸附解吸规律研究[J].
实验力学, 2012, 27 (4) : 492 –497.
Zhang Zhiying, Yang Shengbo. Study on the adsorption and desorption trend of shale gas[J]. Journal of Experimental Mechanics, 2012, 27 (4) : 492 –497. |
| [11] | Guo S. Experimental study on isothermal adsorption of methane gas on three shale samples from Upper Paleozoic strata of the Ordos Basin[J]. Journal of Petroleum Science and Engineering, 2013, 110 : 132 –138. DOI:10.1016/j.petrol.2013.08.048 |
| [12] |
郭为, 熊伟, 高树生, 等. 页岩气等温吸附/解吸特征[J].
中南大学学报:自然科学版, 2013, 44 (7) : 2836 –2840.
Guo Wei, Xiong Wei, Gao Shusheng, et al. Isothermal adsorption/desorption characteristics of shale gas[J]. Journal of Central South University:Science and Technology, 2013, 44 (7) : 2836 –2840. |
| [13] |
闫建萍, 张同伟, 李艳芳, 等. 页岩有机质特征对甲烷吸附的影响[J].
煤炭学报, 2013, 38 (5) : 805 –811.
Yan Jianping, Zhang Tongwei, Li Yanfang, et al. Effect of the organic matter characteristics on methane adsorption in shale[J]. Journal of China Coal Society, 2013, 38 (5) : 805 –811. |
| [14] |
杨峰, 宁正福, 孔德涛, 等. 页岩甲烷吸附等温线拟合模型对比分析[J].
煤炭科学技术, 2013, 41 (11) : 86 –89.
Yang Feng, Ning Zhengfu, Kong Detao, et al. Comparison analysis on model of methane adsorption isotherms inshales[J]. Coal Science and Technology, 2013, 41 (11) : 86 –89. |
| [15] |
盛茂, 李根生, 陈立强, 等. 页岩气超临界吸附机理分析及等温吸附模型的建立[J].
煤炭学报, 2014, 39 (S1) : 179 –183.
Sheng Mao, Li Gensheng, Chen Liqiang, et al. Mechanisms analysis of shale-gas supercritical adsorption and modeling of isorption adsorption[J]. Journal of China Coal Society, 2014, 39 (S1) : 179 –183. |
| [16] | Clarkson C R, Haghshenas B. Modeling of supercritical fluid adsorption on organic-rich shales and coal[C]//SPE Unconventional Resources Conference-USA, Society of Petroleum Engineers, 2013. |
| [17] |
熊健, 梁利喜, 刘向君. 基于吸附势理论的页岩吸附甲烷模型及其应用[J].
成都理工大学学报:自然科学版, 2014, 41 (5) : 604 –611.
Xiong Jian, Liang Lixi, Liu Xiangjun. Study on adsorption model of shale to CH4 based on adsorption potential theory and its application[J]. Journal of Chengdu University of Technology: & Technology Edition, 2014, 41 (5) : 604 –611. |
| [18] | Polanyi M. The potential theory of adsorption[J]. Science, 1963, 141 : 1010 –1013. DOI:10.1126/science.141.3585.1010 |
| [19] | Amankwah K A, Schwarz J A. A modified approach for estimating pseudo-vapor pressures in the application of the Dubinin-Astakhov equation[J]. Carbon, 1995, 33 (9) : 1313 –1319. DOI:10.1016/0008-6223(95)00079-S |
| [20] | Reich R, Ziegler W T, Rogers K A. Adsorption of methane, ethane, and ethylene gases and their binary and ternary mixtures and carbon dioxide on activated carbon at 212301 K and pressures to 35 atmospheres[J]. Industrial and Engineering Chemistry Process Design and Development, 1980, 19 (3) : 336 –344. DOI:10.1021/i260075a002 |
| [21] |
杜晓明, 吴二冬. 应用吸附势理论研究氢在沸石上的超临界吸附[J].
物理化学学报, 2007, 23 (6) : 813 –819.
Du Xiaoming, Wu Erdong. Application of the adsorption potential theory to hydrogen adsorption on zeolites above critical temperature[J]. Acta Physico-Chimica Sinica, 2007, 23 (6) : 813 –819. DOI:10.1016/S1872-1508(07)60047-3 |
| [22] |
崔永君, 李育辉, 张群, 等. 煤吸附甲烷的特征曲线及其在煤层气储集研究中的作用[J].
科学通报, 2005, 50 (S1) : 76 –81.
Cui Yongjun, Li Yuhui, Zhang Qun, et al. The adsorption characteristic curve of coal methane and its role in coalbed methane reservoir research[J]. Chinese Science Bulletin, 2005, 50 (S1) : 76 –81. |
| [23] |
苏现波, 陈润, 林晓英, 等. 吸附势理论在煤层气吸附/解吸中的应用[J].
地质学报, 2008, 82 (10) : 1382 –1389.
Su Xianbo, Chen Run, Lin Xiaoying, et al. Application of adsorption potential theory in the fractionation of coalbed gas during the process of adsorption/desorption[J]. Acta Geologica Sinica, 2008, 82 (10) : 1382 –1389. |
| [24] |
杨宏民, 于保种, 王兆丰. 基于吸附势理论的煤对N2吸附特性的研究[J].
煤矿安全, 2010, 40 (4) : 1 –3.
Yang Hongmin, Yu Baozhong, Wang Zhaofeng. Study on adsorption characteristic of coal to nitrogen based on adsorption potential theory[J]. Safety in Coal Mines, 2010, 40 (4) : 1 –3. |
| [25] |
熊健, 梁利喜, 刘向君, 等. 基于吸附势理论的页岩对甲烷吸附特性[J].
科技导报, 2014, 32 (17) : 19 –22.
Xiong Jian, Liang Lixi, Liu Xiangjun, et al. Adsorption characteristics of shale to CH4 based on adsorption potential theory[J]. Science & Technology Review, 2014, 32 (17) : 19 –22. |
| [26] | Dubinin M M, Astakhov V A. Development of the concepts of volume filling of micropores in the adsorption of gases and vapors by microporous adsorbents[J]. Bulletin of the Academy of Sciences of the USSR, Division of Chemical Science, 1971, 20 (1) : 3 –7. DOI:10.1007/BF00849307 |
| [27] | Do D D. Adsorption Analysis:Equilibria and Kinetics[M]. London: Imperial College Press London, 1998 . |
| [28] | Ozawa S, Kusumi S, Ogino Y J. Physical adsorption of gases at high pressures(IV):An improvement of the Dubinin-Astakhov adsorption equation[J]. Colloid & Interface Science, 1976, 56 : 83 –91. |
| [29] |
范壮军, 何凤艳. Dubinin方程在CO2吸附于活性炭的应用[J].
炭素, 2003, 31 (3) : 3 –8.
Fan Zhuangjun, He Fengyan. Application of CO2 adsorption on activated carbon with Dubinin equation[J]. Carbon, 2003, 31 (3) : 3 –8. |
| [30] | Zhan L, Li K, Zhang R, et al. Improvements of the DA equation for application in hydrogen adsorption at supercritical conditions[J]. The Journal of supercritical fluids, 2004, 28 (1) : 37 –45. DOI:10.1016/S0896-8446(03)00003-2 |
| [31] | Hao S, Chu W, Jiang Q, et al. Methane adsorption characteristics on coal surface above critical temperature through Dubinin Astakhov model and Langmuir model[J]. Colloids and Surfaces A:Physicochemical and Engineering Aspects, 2014, 444 : 104 –113. |
| [32] | 周理.超临界吸附研究疑惑、问题与分析[C].第四届全国氢能学术会议论文集, 2002:154-162. |
| [33] | Dubinin M M. The potential theory of adsorption of gases and vapors for adsorbents with energetically nonuniform surfaces[J]. Chem. Rev., 1960, 60 : 235 –241. DOI:10.1021/cr60204a006 |
| [34] | Dubinin M M. Radushkevich L V[J]. The equation of the characteristic curve of the activated charcoal[J], Proceedings of the USSR Academy of Sciences, Doklady physical chemistry, 1947, 55 : 331 –337. |
| [35] | Reid R C, Sherwood T K. The properties of gases and liquids[M]. New York: McGraw-Hill, 1966 . |
| [36] | NIST. Thermophysical properties of fluid systems[EB/OL]. http://webbook.nist.gov/chemistry/fluid/. |
| [37] |
周亚平, 周理. 超临界氢在活性炭上的吸附等温线研究[J].
物理化学学报, 1997, 13 (2) : 119 –127.
Zhou Yaping, Zhou Li. Study on the adsorption Isotherms of supercritical hydrogen on activated carbon[J]. Acta Physico-Chimica Sinica, 1997, 13 (2) : 119 –127. |
 2015, Vol. 37
2015, Vol. 37


