2. 中国地质大学地球物理与信息技术学院, 北京 海淀 100083;
3. 中国石油大学理学院, 山东 青岛 266580
2. School of Geophysics and Information Technology, China University of Geosciences, Haidian, Beijing 100083, China;
3. College of Science, China University of Petroleum, Qingdao, Shandong 266580, China
在随钻测井仪器出现之前,井下地层的信息是依靠电缆测井获得,其中感应类电阻率测井仪器是最常用的测井仪器之一[1-3]。这类仪器的频率基本在20 kHz左右,收发天线具有多种不同的间距,对应着不同的探测深度,因此测量到的视电阻率曲线中包含着不同探测深度处的电阻率信息。基于几何因子理论,利用软件聚焦技术[4]可以获得固定探测深度处的电阻率值,这对地质解释人员更好地认识地层的侵入特性以及是否存在低阻环带有很大的帮助。随着勘探和开发技术的进步,出现了随钻测井[5-6],随钻电磁波电阻率仪器[7-11]在地层评价中开始发挥越来越大的作用。这类仪器多采用几百千赫兹到几兆赫兹的频率,并且具有多个收发源距,测量的信息中同样包含着多个探测深度处的电阻率信息。由于其与感应类仪器的原理不同,几何因子理论不再适用,且原始的测量曲线探测深度关系不确定,不能与阵列感应曲线直接比较,但工程上常需要在几个月甚至几年后进行阵列感应的测量,并希望通过对两者的比较,获得储层的侵入特性变化及剩余油气体积信息。为解决上述问题,本文提出了一种合成方法,可以得到具有固定探测深度的随钻电磁波电阻率曲线,方便与阵列感应曲线的对比,这对地质解释人员更方便地评价地层特性具有重要的意义。
本文的合成方法通过下面几个步骤实现:首先对测井曲线进行井眼校正,然后利用迭代反演方法同时对围岩及相对倾角进行校正,实现各条曲线的分辨率匹配,之后进行三参数反演得到侵入半径、侵入带电阻率和原状地层电阻率,最后采用提出的伪源距概念实现固定探测深度处视电阻率值计算。由于随钻过程中很多情况下井眼不需要校正,即便校正,方法也非常简单,这里就不再赘述。
1 相对倾角及围岩同时校正的迭代反演方法在垂直井和大斜度井中,随钻电磁波传播电阻率测井仪会受围岩的影响,其中大斜度井中仪器还会受仪器与地层相对倾角的影响[12-16],去除这些影响的传统方法是图版法。这种方法实现简单,但在多点校正时会因工作量大而不适用,因此本文采用了一种基于正演数值模拟的迭代反演方法,此方法适用于多点反演,可以较大限度地消除相对倾角和围岩的影响,改善仪器的分辨率。
1.1 方法原理当地层界面已知时,一般的反演方法都能取得较好的效果。但当地层界面未知,需要从测井曲线中提取时,许多反演方法就难以达到理想的效果。随钻电磁波传播电阻率测井仪大多数都具有对称结构,可以将相位差和幅度比曲线的交点定为地层界面,也可以利用曲线求导的方法获得地层界面。然后采用纵向一维的正演模型,利用格林函数方法[17- 20]实现正演计算,反演时本文采用下面的迭代过程
| $ \left\{ {\begin{array}{*{20}{l}} {\sigma _j^n = {\alpha ^n}\sigma _j^{n-1} + {\beta ^n}\left( {\sigma _j^{{\rm{mea}}}-f_j^{n-1}} \right){\rm{, }}n = 1}\\ {\sigma _j^n = {\alpha ^n}\sigma _j^{n - 1} + {\beta ^n}\left( {\sigma _j^{{\rm{mea}}} - f_j^{n - 1}} \right)\frac{{\sigma _j^{n - 1} - \sigma _j^{n - 2}}}{{f_j^{n - 1} - f_j^{n - 2}}}{\rm{, }}n > 1} \end{array}} \right. $ | (1) |
式中:
在进行围岩及相对倾角校正时,通常选分辨率较高的曲线,本例中选取仪器的频率为2 mHz,源距为0.508 m,两接收线圈间距为0.2032 m,仪器和地层的相对倾角为60°,地层模型选为Oklahoma地层,该地层的层厚和相邻两层的电阻率对比度变化范围较广,是验证算法常用的典型地层。反演中地层边界采用曲线求导的方式获得,模拟结果见图 1。观察发现,大多数地层的反演结果与真值基本吻合,只是在上百欧姆米的高阻层时结果与真值存在很小偏差,这主要是曲线求导获得的边界与真实值存在差异造成的,并不影响该方法的有效性。
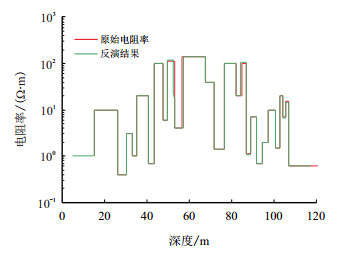 |
| 图1 反演结果 Fig. 1 Result of inversion |
完成围岩校正后,可以近似认为仪器在每层中的响应只受侵入的影响,可以采用径向一维反演获得侵入带电阻率、侵入半径及原状地层电阻率三参数。本文的反演方法采用高斯牛顿梯度下降法。
2.1 高斯牛顿-梯度下降法在给定反演初始值
| $ \min \left\{ {\left\| {\boldsymbol{b} -\boldsymbol{J} \delta \boldsymbol{} \boldsymbol{x}} \right\|:\left\| {\delta \boldsymbol{x} } \right\| \le \Delta } \right\} $ | (2) |
式中:
b=f-F(xc)—函数值的差;
f—实测的响应值;
F(xc)—模拟计算的响应值;
J—雅可比矩阵;
δx—待求解的参数x的变化量;
Δ—参数变化量的约束值。
根据给定的初始值求解式(2)得到δx值,则更新后x=xc+δx,这种方法的重点在于如何计算式(2),首先对雅可比矩阵J进行奇异值分解,如式(3)
| $ \boldsymbol{J} = \boldsymbol{Y}\mathit{\pmb{\Lambda}} {\boldsymbol{V}^{\rm{T}}} $ | (3) |
其中,U和V分别为M×N和N×N阶矩阵,且满足UTU=VTV=I,I为单位矩阵,Λ为N×N阶的对角矩阵,包含奇异值
| $ {\lambda _1} \ge {\lambda _2} \ge \cdots \ge {\lambda _j} \ge \cdots \ge {\lambda _p} > 0, \\ {\lambda _{p + 1}} = {\lambda _{p + 2}} = \cdots = {\lambda _N} = 0 $ | (4) |
其中,p为雅可比矩阵J的秩。若不考虑约束条件
| $ \delta \boldsymbol{x} = \boldsymbol{V}{\mathit{\pmb{\Lambda}} ^{ - 1}}\boldsymbol{g} $ | (5) |
其中,g=UTb, Λ的元素为
| $ \left\{ {\begin{array}{*{20}{c}} {\Lambda _{jj}^{-1} = 1/{\lambda _j}{\rm{, }}{\lambda _j} > 0}\\ {\Lambda _{jj}^{-1} = 0{\rm{, 其他}}} \end{array}} \right. $ | (6) |
实际求解式(2)时,由于非零奇异值有可能很小,容易出现上溢,因此,为了使迭代过程稳定,引进阻尼因子
| $ \delta \boldsymbol{x}\left( \mu \right) = \boldsymbol{V}{\left( {{\mathit{\pmb{\Lambda}} ^2} + \mu \boldsymbol{I}} \right)^{ - 1}}\mathit{\pmb{\Lambda}} \boldsymbol{g} $ | (7) |
当μ=0,
| $ \phi \left( \mu \right) = \left\| {\delta \boldsymbol{x} \left( \mu \right)} \right\|-\Delta = 0 $ | (8) |
则相应的
| $ {\mu ^{k + 1}} = {\mu ^k}-\left( {\left\| {\delta {\bf\boldsymbol {x}}\left( {{\mu ^k}} \right)} \right\|/\Delta } \right)\phi \left( {{\mu ^k}} \right)/\phi '\left( {{\mu ^k}} \right) $ | (9) |
其中
| $ \phi '\left( {{\mu ^k}} \right) = \frac{{[\delta \boldsymbol{x} {{\left( {{\mu ^k}} \right)}^{\rm{T}}}\boldsymbol{V} {{\left( {{\mathit{\pmb{\Lambda}} ^2} + {\mu ^k}\boldsymbol{I} } \right)}^{-1}}{\boldsymbol{U} ^{\rm{T}}}\delta x\left( {{\mu ^k}} \right)]}}{{\left\| {\delta {\bf\boldsymbol {x}}\left( {{\mu ^k}} \right)} \right\|}} $ | (10) |
选择仪器的频率为2 mHz和400 kHz,源距为0.5080,0.7620,1.1684 m,两个接收线圈间距为0.2032 m。给定侵入电阻率Rxo=1.0Ω·m,原状地层电阻率
| 表1 迭代结果 Table 1 Result of iteration |
通过其他模拟算例发现,只要不选择与侵入电阻率或真实电阻率值相近的视电阻率曲线,都能反演出满意的结果,并且只需几步迭代即可,说明了该反演方法的有效性和快速性。
3 固定探测深度曲线实现方法获得地层的侵入带电阻率、侵入半径及原状地层电阻率之后,利用提出的伪源距的概念,对固定探测深度处的视电阻率值进行计算。
3.1 探测深度的定义随钻电磁波电阻率测井仪的探测深度[21]常定义为侵入带电导率与原状地层电导率对仪器响应的贡献各占50%时的侵入半径深度。假如选取泥浆电阻率Rm=0.06 Ω·m,侵入电阻率Rxo=0.55 Ω·m,原状地层电阻率Rt=30.0 Ω·m的地层,钻铤直径为0.1778 m,井眼直径为0.2032 m,计算的视电阻率随侵入半径变化的曲线见图 2。图中的横直线代表 50%的响应值,每条曲线与该横线的交点处向下的箭头所指的侵入半径即为该曲线的探测深度。图中的2 MHz 0.5080 m Rp和2 MHz 0.5080 m Ra分别代表频率为2 MHz,源距为0.5080 m的相位差视电阻率值和幅度比视电阻率值,其余曲线标识的含义与之类似。
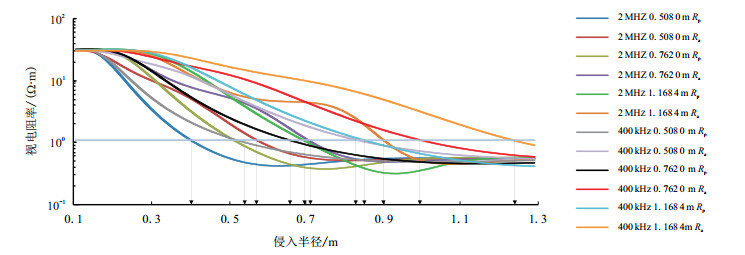 |
| 图2 探测深度曲线 Fig. 2 Curves of depth of investigation |
经过三参数反演得到Rxo和Rt后,按照上节描述的探测深度的计算方法,计算不同频率和不同源距下的探测深度值,曲线见图 3。
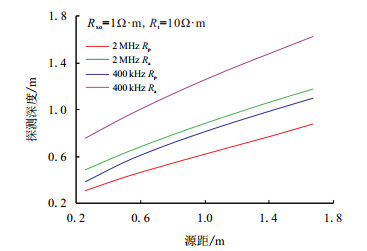 |
| 图3 探测深度与源距的关系曲线 Fig. 3 Relationship curves between depth of investigation and spacing |
观察发现,探测深度与源距的关系基本成一平滑的曲线。将要合成的探测深度值在图 3中进行插值,得到的源距称之为与固定探测深度对应的伪源距。
3.3 固定探测深度处视电阻率计算利用得到的Rxo、Rt和r,计算不同频率下,仪器在此径向二层地层模型中视电阻率随源距的变化曲线,见图 4。
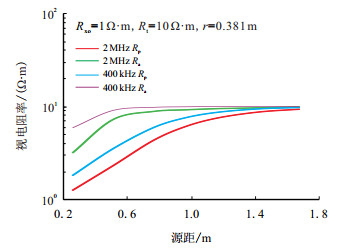 |
| 图4 视电阻率与源距的关系 Fig. 4 Relationship between apparent resistivity and spacing |
观察图 4发现,视电阻率与源距的关系也基本呈平滑的曲线,利用上节得到的伪源距在图 4上进行插值,便得到固定探测深度处的视电阻率值。
3.4 数值举例以三层地层为例,模型1假设围岩电阻率为Rs,目的层厚d=2 m,目的层Rxo=1.0 Ω·m,Rt=10.0Ω·m,r=0.381 m,采用混合法[14]进行正演模拟,结果见图 5,图中2 MHz 0.5080 m表示频率为2 MHz,源距为0.5080 m时的视电阻率曲线,其余曲线含义与之类似。选取固定探测深度为0.2540,0.5080,0.7620,1.0160和1.5240 m。利用上面介绍的方法和绘制的多个图版,通过两次插值得出固定探测深度处的视电阻率。计算结果如表 2。
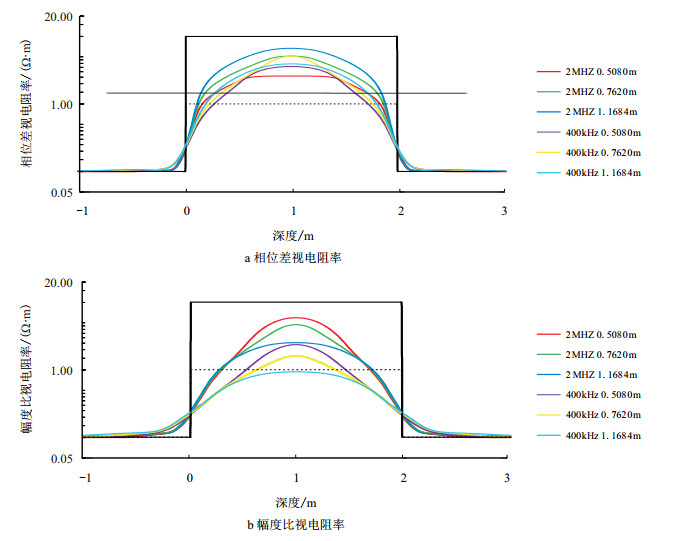 |
| 图5 模型1正演曲线 Fig. 5 Forward logs of model 1 |
| 表2 固定探测深度处视电阻率 Table 2 Apparent resistivity in fixed depth of investigation |
在插值计算过程中,发现外插的精度要低于内插的精度,因此,计算探测深度为0.2540及0.5080 m的电阻率时应尽量选取2 MHz的工作频率,而计算0.7620,1.0160和1.524 m时应尽量选取400 kHz的工作频率。在实际中应根据具体情况进行合理地选择,尽量让固定探测深度处的视电阻率由内插值得到。此例中,0.2540 m和0.5080 m选择2 MHz的相位差视电阻率,0.7620 m选择2 MHz的幅度比视电阻率,1.0160 m选择400 kHz的相位差视电阻率,1.5240 m选择400 kHz的幅度比视电阻率。合成后的曲线应该是矩形脉冲形式,为了与常规的测井曲线相比较,将其处理成图 6所示的形式。
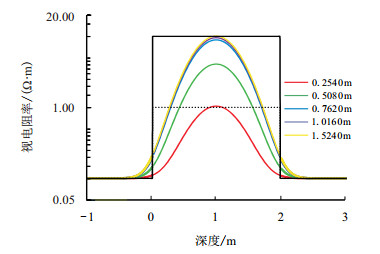 |
| 图6 模型1具有固定探测深度的测井曲线 Fig. 6 Logs in fixed depth of investigation of model 1 |
观察图 5发现,由于受侵入和围岩的影响,很难利用图 5的正演测井曲线很好地判断目的层的侵入特性,而从图 6可以清楚地看出,随着探测深度的增加,电阻率逐渐增大,是典型的低侵特征。0.2540 m深度处的电阻率反映的是侵入带的电阻率,0.5080 m深度处的电阻率受侵入和原状地层共同的影响介于两者之间,由于侵入半径为0.381 m,因此,0.7620,1.0160和1.5240 m的曲线基本反映的是原状地层的电阻率,且1.524 m的值与原状地层的电阻率值能很好地吻合。
为进一步说明方法的有效性,模型2将上例中的层厚由2.0 m减小到0.6 m,其余参数不变,考察该方法在薄层中的应用。正演曲线和合成后的曲线见图 7、图 8。
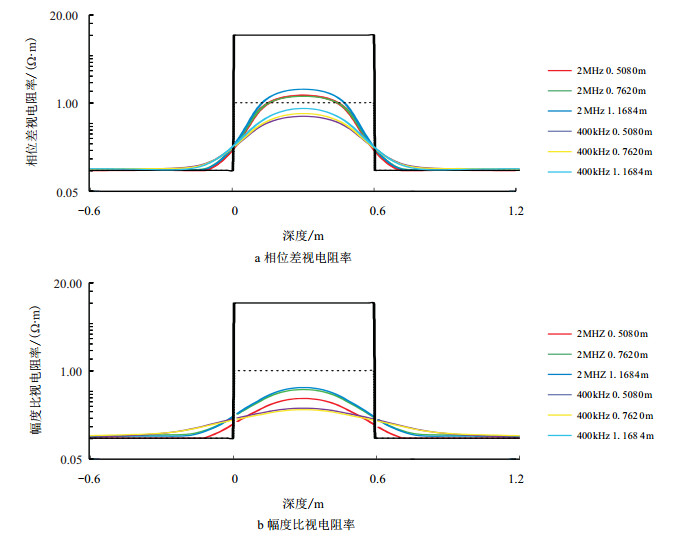 |
| 图7 模型2正演曲线 Fig. 7 Forward logs of Model 2 |
 |
| 图8 模型2具有固定探测深度的测井曲线 Fig. 8 Logs in fixed depth of investigation of Model 2 |
从图 7中看出,由于仪器在薄层中受围岩的影响严重,曲线的值明显低于层厚为2.0 m时的值,而且从曲线的形态很难判断出地层参数的径向分布特性。观察图 8,由于层厚较薄,受围岩的影响严重,致使深探测的合成曲线也无法反映地层的真实电阻率,但曲线随探测深度变化的特征完全和层厚2.0 m的一致,能反映地层径向的电参数分布特性,因此,通过上面两个算例,可以说明本文提出的方法是有效的,能够帮助地质解释人员更好地认识地层剖面,实现更准确的地层评价。
4 结论(1) 合成的具有固定探测深度的曲线相比原始曲线能很好地反映地层在径向上的变化特征,有助于地质解释人员更好地利用该特征进行地层评价,提升了该仪器的应用价值。
(2) 厚层时,合成的深探测视电阻率值能基本反映真实的地层电阻率值,结果比较可靠。
(3) 薄层时,由于受围岩影响严重而无法反映地层的真实电阻率值,但曲线反映的径向特征规律正确,说明该方法在薄层下仍然具有一定的应用价值。
| [1] | 刘智涌.相位感应测井仪器设计及其信号处理研究[D].成都:电子科技大学, 2003. http://cdmd.cnki.com.cn/article/cdmd-10614-2003120360.htm |
| [2] |
肖加奇, 张国艳, 洪德成, 等. 层状各向异性地层中三维感应测井响应快速计算及资料处理[J].
地球物理学报, 2013, 56 (2) : 696 –706.
Xiao Jiaqi, Zhang Guoyan, Hong Decheng, et al. Fast forward modeling and date processing of 3D induction logging tool in layered anisotropic formation[J]. Chinese Journal of Geophysics, 2013, 56 (2) : 696 –706. |
| [3] |
王昌学, 储昭坦, 肖承文, 等. 井环境对阵列感应测井响应的影响分析[J].
地球物理学报, 2013, 56 (4) : 1392 –1403.
Wang Changxue, Chu Zhaotan, Xiao Chengwen, et al. The analysis of effect of the borehole environment on responses of array induction logging[J]. Chinese Journal of Geophysics, 2013, 56 (4) : 1392 –1403. |
| [4] | 杨长平.阵列感应测井中信号聚焦的分析及应用[D].天津:天津大学, 2009. http://cdmd.cnki.com.cn/article/cdmd-10056-2010091652.htm |
| [5] |
张辛耘, 郭彦军, 王敬农. 随钻测井的昨天、今天和明天[J].
测井技术, 2006, 30 (6) : 487 –492.
Zhang Xinyun, Guo Yanjun, Wang Jingnong. The logging while drilling:Past, present and future[J]. Well Logging Technology, 2006, 30 (6) : 487 –492. |
| [6] |
邹晓萍, 陈恭洋. 边际油田薄油层开发中的地质导向技术[J].
西南石油大学学报:自然科学版, 2013, 35 (5) : 65 –72.
Zou Xiaoping, Chen Gongyang. Application of geosteering technique in the marginal oil sheet developing[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2013, 35 (5) : 65 –72. |
| [7] | Coope D, Shen L C, Huang F S C. The theory of 2 MHz resistivity tool and its application to measurement-whiledrilling[J]. The Log Analyst, 1984, 25 (3) : 1 –11. |
| [8] |
刘四新, 佟文琪. 电磁波测井的现状和发展趋势[J].
地球物理学进展, 2004, 19 (2) : 235 –237.
Liu Sixin, Tong Wenqi. The situation and progress of electromagnetic well logging[J]. Progress in Geophysics, 2004, 19 (2) : 235 –237. |
| [9] |
陈爱新. 随钻电阻率测井仪器探测特性分析[J].
天然气工业, 2007, 27 (5) : 61 –62.
Chen Aixin. Instrument analysis of resistivity logging while drilling[J]. Natural Gas Industy, 2007, 27 (5) : 61 –62. |
| [10] |
张旭, 魏宝君, 刘坤, 等. 利用积分方程的加速迭代算法计算随钻电磁波电阻率测量仪器的响应[J].
地球物理学报, 2009, 52 (9) : 2394 –2401.
Zhang Xu, Wei Baojun, Liu Kun, et al. Computing electromagnetic wave resistivity MWD tool's response using accelerated iteration algorithm for integral equations[J]. Chinese Journal of Geophysics, 2009, 52 (9) : 2394 –2401. |
| [11] |
刘得军, 马中华, 苑赫, 等. 自适应高阶矢量有限元方法在随钻电阻率测井中的应用[J].
中国石油大学学报:自然科学版, 2012, 36 (4) : 77 –83, 92.
Liu Dejun, Ma Zhonghua, Yuan He, et al. Application of adaptive higher-order vector finite element method to simulate resistivity logging-while-drilling tool response[J]. Journal of China University of Petroleum, 2012, 36 (4) : 77 –83, 92. |
| [12] |
杨震, 刘庆成, 岳步江, 等. 随钻电磁波电阻率测井仪器响应影响因素数值模拟[J].
测井技术, 2011, 35 (4) : 325 –330.
Yang Zhen, Liu Qingcheng, Yue Bujiang, et al. Numerical simulation on influence factors of electromagnetic wave resistivity logging while drilling response[J]. Well Logging Technology, 2011, 35 (4) : 325 –330. |
| [13] |
孙向阳, 聂在平, 赵延文, 等. 用矢量有限元方法模拟随钻测井仪在倾斜各向异性地层中的电磁响应[J].
地球物理学报, 2008, 51 (5) : 1600 –1607.
Sun Xiangyang, Nie Zaiping, Zhao Yanwen, et al. The electromagnetic modeling of logging while drilling tool in tilted anisotropic formations using vector finite element method[J]. Chinese Journal of Geophysics, 2008, 51 (5) : 1600 –1607. |
| [14] |
沈金松. 用边有限元法计算三维各向异性介质的电磁响应[J].
测井技术, 2004, 28 (1) : 11 –15.
Shen Jinsong. Modeling of the 3-D electromagnetic response to the anisotropic medium by the edge finite element method[J]. Well Logging Technology, 2004, 28 (1) : 11 –15. |
| [15] |
文艺, 韩晓梅. 大斜度井随钻电磁波层厚影响模拟及机理分析[J].
西南石油大学学报:自然科学版, 2013, 35 (4) : 75 –80.
Wen Yi, Han Xiaomei. Simulation of bed thickness effect and mechanism analysis of electromagnetic wave resistivity logging while drilling in highly deviated wells[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2013, 35 (4) : 75 –80. |
| [16] |
刘红岐, 夏宏泉, 郭璞, 等. 随钻电阻率测井介电效应校正图版分析及方法[J].
西南石油大学学报:自然科学版, 2010, 32 (2) : 58 –63.
Liu Hongqi, Xia Hongquan, Guo Pu, et al. Study on the correction chart for dielectric effect of resistivity logging while drilling[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2010, 32 (2) : 58 –63. |
| [17] |
魏宝君, 张庚骥, 柳清伙. 层状单轴各向异性介质并矢Green函数的递推算法及精确计算[J].
中国科学E辑:信息科学, 2007, 37 (6) : 63 –80.
Wei Baojun, Zhang Gengji, Liu Qinghuo. Recursive algorithm and accurate computation of dyadic Green's function for stratified uniaxial anisotropic media[J]. Science in China:Series E, 2007, 37 (6) : 63 –80. |
| [18] |
杨锦舟, 魏宝君, 林楠. 径向成层介质的Green函数及其在随钻电磁波电阻率测量中的应用[J].
中国石油大学学报:自然科学版, 2009, 33 (3) : 53 –58.
Yang Jinzhou, Wei Baojun, Lin Lan. Green's function for radial stratified media and its application to electromagnetic wave resistivity measurement while drilling tool[J]. Journal of China University of Petroleum:Edition of Natural Science, 2009, 33 (3) : 53 –58. |
| [19] |
魏宝君, 张克, 欧永峰, 等. 采用混合法和递推矩阵算法模拟层状介质中随钻电磁波电阻率测量仪器的响应[J].
中国石油大学学报:自然科学版, 2013, 37 (1) : 61 –69.
Wei Baojun, Zhang Ke, Ou Yongfeng, et al. Simulating electromagnetic wave resistivity MWD tool's response in stratified media using hybrid method and recursive matrix algorithm[J]. Journal of China University of Petroleum, 2013, 37 (1) : 61 –69. |
| [20] |
魏宝君, 王莎莎, 欧永峰. 用并矢Green函数的矢量本征函数展开式模拟随钻感应测井仪器的响应[J].
地球物理学报, 2011, 54 (5) : 1391 –1401.
Wei Baojun, Wang Shasha, Ou Yongfeng. Simiulation the response of induction logging while drilling tools by vector eigenfuntion expansion formulae for dyadic Green's functions[J]. Chinese Journal of Geophysics, 2011, 54 (5) : 1391 –1401. |
| [21] |
史晓锋, 李铮, 蔡志权. 随钻电磁波传播电阻率测量工具探测深度研究[J].
测井技术, 2002, 26 (2) : 113 –117.
Shi Xiaofeng, Li Zheng, Cai Zhiquan. Investigation depth of MWD propagation resistivity logging[J]. Well Logging Technology, 2002, 26 (2) : 113 –117. |
 2015, Vol. 37
2015, Vol. 37


