2. 中海油研究总院, 北京 朝阳 100028;
3. 中国石油长庆油田分公司, 陕西 西安 710018;
4. 中海石油(中国)有限公司天津分公司, 天津 塘沽 300452
2. CNOOC Research Institute, Chaoyang, Beijing 100028, China;
3. Changqing Oilfield Branch, CNPC, Xi'an, Shaanxi 710018, China;
4. Tianjin Branch(China), CNOOC, Tanggu, Tianjin 300452, China
对于注水开发油田,受储层非均质的影响,油藏中某些部位会出现注入水快速突破、注入孔隙体积倍数高、无效水循环等特征,导致驱替过程不均衡,进而影响油田的开发效果。为了使得驱替过程更加均衡,提高采收率,获得更高的经济效益,有必要在布井时进行井网优化设计,充分考虑储层的非均质性,布置与其相匹配的井网[1-4]。目前,在井网优化设计中,经常使用油井见水时间和面积波及系数等指标作为井网优化的目标函数[5-6]。但是用这些指标作为优化的目标函数存在不足:如油井见水时间和面积波及系数都不能单独作为表征均衡驱替的参数和均衡驱替判别的充分条件,因为见水时间相同只能反映注采连线上的驱替速度相同,不能反映油藏其他部位的驱替状况,而面积波及系数最大时,被波及部位的驱替程度不同,含油饱和度有较大差异,某些部位注入水大量无效循环,不能反映开发过程中驱替的均衡性。本文依据均衡驱替的最主要特征就是注入水的波及范围大,各部位的剩余油饱和度差异较小,同时还表现为注入水在各个方向上均匀推进,注水效率高等[5],因此引入油藏流场强度作为表征均衡驱替的参数,并以油藏流场强度变异系数作为井网优化的目标函数。油藏流场是指油气存储空间和存储流体以及流体在油藏中的变化规律的总称[7]。油藏流场强度大的部位注入水流动能力强,水驱效果好;油藏流场强度小的部位表示注入水很少波及,水驱效果较差,油藏流场能直观展示储层的流体流动和分布状态,可以反映储层驱替均衡程度和井网布置是否合理。
1 油藏流场强度的确定 1.1 评价指标集的选取油藏流场是一个多因素相互影响、相互作用的复杂体系,需综合考虑影响油藏流场的各项因素。油藏流场评价指标可分为地质因素和开发因素两类。地质因素主要包括孔隙度、岩石渗透率、有效厚度、岩石和流体压缩系数等。开发因素主要包括注采比、注入水流速、含水饱和度、井网形式、累积注水量等。
各种指标对油藏流场的影响程度不尽相同,有些指标对流场的影响是重复的,有些指标虽然是独立的,但对油藏流场的影响较小,因此,首先要对评价指标进行筛选。静态因素无法调整,但其影响可以通过这些开发指标反映出来。本文主要采用逻辑分析法,将影响流场的指标按因果关系、等价关系和过程关系分类,剔除原因、等价多余和过程等指标,选择对油藏流场影响程度较大的过水倍数、流体流速和含水饱和度3个评价指标,建立油藏流场定量描述的评价指标集[8]。
1.2 流场强度的计算过水倍数是指单位孔隙体积内累积通过注入水的体积倍数,它反映的是注入水对油藏在时间的累积效应;流体流速是指单位时间内通过单位储层截面积的流体流量,它反映的是注入水在油藏中的瞬时流动状态;含水饱和度反映的是油藏中油水的分布状态。在这里,把由过水倍数、流体流速和含水饱和度3者确定的油藏流场的大小定义为油藏流场强度。为研究需要,把油藏网格化处理,以网格为基本对象研究各网格的油藏流场强度,进而确定整个油藏的流场分布。
过水倍数、流体流速和含水饱和度越大,对油藏流场的影响越大,流场强度越大。因此采用升梯形法来确定它们对油藏流场强度的隶属函数。
简化的升梯形法分布模式为
| $ {\mu _{\rm{A}}}(x) = \frac{{x - {a_1}}}{{{a_2} - {a_1}}},{a_1} \le x \le {a_2} $ | (1) |
式中:a1,a2—相应参数的最小和最大值;x—相应参数的取值;μA(x)—相应参数x的隶属度,无因次。
根据3个指标对油藏流场影响程度的大小,依据层次分析法的专家打分法建立评价指标权重的评判矩阵,如表 1所示。
| 表1 评价指标评判矩阵 Table 1 Evaluation matrix of the evaluation index |
经过一致性校验,求得评价指标的权重向量为
| $ \boldsymbol{\omega} = {(0.5085,0.2933,0.1982)^{\rm{T}}} $ | (2) |
式中:ω—权重向量,无因次。
油藏流场强度的表达式为
| $ \boldsymbol{W} = \boldsymbol{X}\boldsymbol{\omega} $ | (3) |
| $ \boldsymbol{X}\left\{ {\begin{array}{*{20}{c}} {{x_{11}}}&{{x_{12}}}&{{x_{13}}}\\ \cdots & \cdots & \cdots \\ {{x_{m1}}}&{{x_{m2}}}&{{x_{m3}}} \end{array}} \right\} $ | (4) |
式中:W—油藏流场强度,无因次;X—评价指标集,由相应的隶属度函数确定。
2 井网优化数学模型的建立和求解井网优化是通过调整油田区块内油水井的井位,使得油藏流场分布均匀,进而改善水驱开发效果,获得更高的经济效益,是一个典型的最优化问题[9-11]。与单井组优化不同,井网整体优化中,井组之间相互制约,相互影响,减小某口井在某井组的井距,可能导致其在另一井组的井距增大,因此,优化时,不能孤立出单个井组进行优化,而应把井网看成一个整体,对每口井进行优化。
2.1 目标函数井网优化就是通过井网中各口井的井位调整,匹配油藏的非均质性,使得油藏流场分布均匀,从而最大化的实现均衡驱替。在统计学上用变异系数来衡量一组数据离散程度的大小,本文通过定义油藏流场变异系数来表征油藏流场分布的均匀程度,油藏流场变异系数越大,表示油藏流场分布越不均匀,油藏流场变异系数越小,表示油藏流场分布越均匀,因此取油藏流场强度变异系数最小作为井网优化的目标。
| $ \min F\left( \boldsymbol{W} \right) = \sqrt {\frac{{{{\sum\limits_{i = 1}^n {\left( {{W_i} - \frac{1}{n}\sum\limits_{i = 1}^n {{W_i}} } \right)} }^2}}}{{n - 1}}} \cdot \frac{n}{{\sum\limits_{i = 1}^n {{W_i}} }} $ | (5) |
式中:Wi—各网格的流场强度,无因次;F(W)—各网格流场强度的变异系数,无因次;n—总的网格数。
2.2 约束条件优化过程中需要对井位优化变量进行必要的约束,在井网优化过程中,各口井的位置不可超出油田边界,且任意两口井之间的距离不可太小,否则在经济上不可行[12-13]。基于以上考虑,给出以下约束条件
| $ \left( {{x_i},{y_i}} \right) \in \mathit{\Omega} \;\;\;\;i = 1,2 \cdots m $ | (6) |
| $ \begin{align} & {{d}_{ij}}=\sqrt{{{\left( {{x}_{i}}-{{x}_{j}} \right)}^{2}}+{{\left( {{y}_{i}}-{{y}_{j}} \right)}^{2}}}≥{{d}_{\min }} \\ & i=1,2\cdots m;j=1,2\cdots m \\ \end{align} $ | (7) |
式中:xi,yi,xj,yj—第i、j口井的x向和y向坐标,m;Ω—油藏边界;dij—第i口井和第j口井之间的距离,m;dmin—最小井距,m;m—总井数,口。
综上,井网优化问题可以表述为:在井位变量满足非线性约束条件(6)和(7),求解使目标函数F(W)取得最小值的最优井位(xi*, yi*),i=1, 2, …m。
2.3 数学模型的求解目前求解大型多维优化模型的方法主要有梯度类算法和搜索类算法。根据井网优化数学模型,井位优化是一个大尺度、多峰值、有约束的优化问题,梯度的获取很困难。通常采用伴随方法和离散极大值原理来求取梯度,但是该方法需要将伴随矩阵嵌入到油藏数值模拟计算中,求解过程非常复杂[14]。因此,梯度类算法目前仍无法较好地应用于实际井网优化问题的求解。通过对比各种优化算法的优缺点,本文选取遗传算法(GA)作为数学模型的求解算法[15]。遗传算法(GA)在求解井网优化数学模型时,根据优化模型规模选择适当的种群数量和迭代步数,避免搜索过程陷入局部最优解,同时根据个体适应度值选择合适的交叉与变异概率,使井网优化过程中,能更好地确定最优的井位调整方向和位置[16]。遗传算法求解井网优化数学模型的求解流程图见图 1,其基本计算步骤如下:
 |
| 图1 求解流程图 Fig. 1 Solution flow diagram |
(1) 选定一组井网井位方案作为初始种群;
(2) 将各初始方案分别写进数值模拟器井处理文件中;
(3) 运行数值模拟器,得到油藏压力和饱和度分布;
(4) 根据压力和饱和度计算油藏流场强度及其变异系数(目标函数);
(5) 对井网方案种群进行交叉变异操作,并计算相应的目标函数值;
(6) 对种群进行选择操作,构成下一代井网方案种群,并保留每一代流场强度变异系数最小(目标函数值)的井网井位方案;
(7) 判断是否满足停止准则,若满足,则停止迭代,输出所保留流场强度变异系数(目标函数)最小的井网井位方案;否则,转至步骤(2),继续进行迭代求解。
3 实例分析以某实际油田为算例,构建油藏流场概念模型,网格数为48×48×1,网格大小为Δx=Δy=30 m,Δz=10 m。概念模型采用反九点法井网,井网排距360 m,井距360 m。为反映实际模型的特点,平面渗透率分布以变异系数为0.5随机产生,残余油饱和度为25%,束缚水饱和度为30%,其相对渗透率曲线如图 2所示。
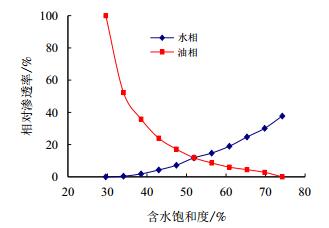 |
| 图2 油水相对渗透率曲线 Fig. 2 Curve of oil and water relative permeability |
模型共25口井(图 3),其中A01、C03、D05、C11、G13、C15、A21、C23、A25等9口为水井,其余16口为油井,各井的注采量按照产量劈分原理分配,对于油井来说,边井的产液量为100 m3/d,中心油井产液量为200 m3/d;对于注水井来说,角井的注入量为50 m3/d,边井的注入量为100 m3/d,中心G13的注入量为200 m3/d,油藏整体保持总注入量为800 m3/d,地面注采比1:1。为了对比井网优化前后的效果,在井网优化过程中,各口井的注入量和采出量都保持不变。以此模型为基础研究井网优化前后油藏流场强度的变化,并表征井网优化前和优化后的油藏流场变异系数。
 |
| 图3 优化前后油藏流场分布对比 Fig. 3 Comparison of reservoir flow field before and after optimization |
从井网优化前后的油藏流场分布对比图(图 3)可以看出,优化前的反九点规则井网由于没有油藏平面非均质性的影响,注水生产到后期时,注入水突进现象很严重,特别是中心注水井G13和边井注水井C03、C11、C15、C23之间过水倍数较大,注入水大量无效循环,油藏流场强度较大,而在G13与E07,C16与E07之间的区域油藏流场强度较小,注入水几乎没有波及,从而导致整体上油藏流场分布不均,注入水驱替不均衡;通过以油藏流场变异系数最小为优化目标对井网井位进行优化后,井网不再是规则的,这种不规则的井网与储层非均质性相匹配,使得优化后油藏流场分布变得均匀,注入水突进现象减弱,注水驱替较井位优化前均衡。
为了对比井网优化前和优化后的开发效果,将优化前后的井位结果输入到数值模拟软件进行开发指标计算,通过比较井位优化前后的采出程度与含水率曲线(图 4)可以看出,采用优化后的井网进行开采,由于井网适应储层的非均质性,油藏流场分布均匀,含水上升较慢,而且在相同采出程度下,优化后井网的含水率更低,并提高了最终采收率。
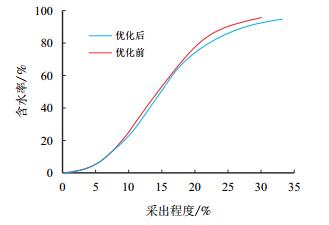 |
| 图4 优化前后采出程度与含水率曲线对比 Fig. 4 Comparison of water-cut vs. recovery percent curve before and after optimization |
(1) 选用对油藏流场影响较大的过水倍数、流体速度和含水饱和度3个指标作为油藏流场描述的评价指标集,应用模糊数学和层次分析法定量表征了油藏流场,并用油藏流场作为表征均衡驱替的标准。
(2) 建立了井网整体优化数学模型,定义了油藏流场强度变异系数概念,并以油藏流场强度变异系数最小作为优化目标,对油田井网中每一口井的井位进行调整,以实现最大化均衡驱替。
(3) 该方法可以实现井网与储层非均质的最大程度上的匹配,能改善水驱状况和提高最终采收率。
| [1] | Ramey Jr H J. Interference analysis for anisotropic formations-a case history[J]. Journal of Petroleum Technology, 1975, 27 (10) : 1290 –1298. DOI:10.2118/5319-PA |
| [2] | Rose W. Permeability anisotropy in low permeability formations[C]. SPE 10810, 1982. |
| [3] |
丁云宏, 曾斌. 渗透率各向异性的低渗透油藏开发井网研究[J].
石油学报, 2002, 23 (2) : 64 –67.
Ding Yunhong, Zeng Bin. The development well-pattern of low and anisotropic permeability reservoirs[J]. Acta Petrolei Sinica, 2002, 23 (2) : 64 –67. |
| [4] |
刘月田. 各向异性油藏注水开发布井理论与方法[J].
石油勘探与开发, 2005, 32 (5) : 101 –104.
Liu Yuetian. Well location in water-flooding anisotropic oil reservoirs[J]. Petroleum Exploration and Development, 2005, 32 (5) : 101 –104. |
| [5] |
王德龙, 郭平, 汪周华, 等. 非均质油藏注采井组均衡驱替效果研究[J].
西南石油大学学报:自然科学版, 2011, 33 (5) : 122 –125.
Wang Delong, Guo Ping, Wang Zhouhua, et al. Study on equilibrium displacement effects of injection-production well group in heterogeneous reservoirs[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2011, 33 (5) : 122 –125. |
| [6] |
李传亮, 李炼民. 各向异性地层的井距设计研究[J].
新疆石油地质, 2003, 24 (6) : 559 –561.
Li Chuanliang, Li Lianmin. Well spacing design for anisotropic reservoirs[J]. Xinjiang Petroleum Geology, 2003, 24 (6) : 559 –561. |
| [7] |
辛治国, 贾俊山, 孙波. 优势流场发育阶段定量确定方法研究[J].
西南石油大学学报:自然科学版, 2012, 34 (2) : 119 –124.
Xin Zhiguo, Jia Junshan, Sun Bo. Research on the quantitative determination of the dominant flow field development stages[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2012, 34 (2) : 119 –124. |
| [8] |
姜瑞忠, 刘小波, 王海江, 等. 指标综合筛选方法在高含水油田开发效果评价中的应用:以埕东油田为例[J].
油气地质与采收率, 2008, 15 (2) : 99 –101.
Jiang Ruizhong, Liu Xiaobo, Wang Haijiang, et al. Application of variables synthetical selection in the production effect evaluation for oilfield in high water-cut period[J]. PGRE, 2008, 15 (2) : 99 –101. |
| [9] | Beckner B L, Song X. Field development planning using simulated annealing-optimal economic well scheduling and placement[C]. SPE 30650, 1995. |
| [10] | Hazlett R, Babu D. Optimal well placement in heterogeneous reservoirs via semi-analytic modeling[J]. SPE Journal, 2005, 10 (3) : 286 –296. DOI:10.2118/84281-PA |
| [11] | Abukhamsin A Y. Optimization of well design and location in a real field[D]. California:Stanford University, 2009. |
| [12] |
张凯, 李阳, 姚军, 等. 油藏生产优化理论研究[J].
石油学报, 2010, 31 (1) : 78 –83.
Zhang Kai, Li Yang, Yao Jun, et al. Theoretical research on production optimization of oil reservoirs[J]. Acta Petrolei Sinica, 2010, 31 (1) : 78 –83. |
| [13] | 姜汉桥, 姚军, 姜瑞忠. 油藏工程原理与方法[M]. 北京: 中国石油大学出版社, 2006 . |
| [14] | Onwunalu J. Optimization of field development using particle swarm optimization and new well pattern descriptions[D]. California:Stanford University, 2010. |
| [15] | Emerick A, Silva E, Messer B, et al. Well placement optimization using a genetic algorithm with nonlinear constraints[C]. SPE 118808, 2009. |
| [16] |
关晓晶, 魏立新, 杨建军. 基于混合遗传算法的油田注水系统运行方案优化模型[J].
石油学报, 2005, 26 (3) : 114 –117.
Guan Xiaojing, Wei Lixin, Yang Jianjun. Optimization of operation plan for water injection system in oilfield using hybrid genetic algorithm[J]. Acta Petrolei Sinica, 2005, 26 (3) : 114 –117. |
 2015, Vol. 37
2015, Vol. 37


