2. 西安石油大学电子工程学院, 陕西 西安 710065;
3. 重庆理工大学电子信息与自动化学院, 重庆 沙坪坝 400054
2. College of Electronic Engineering, Xi'an Shiyou University, Xi'an, Shaanxi 710065, China;
3. College of Electronic Information & Automation, Chongqing University of Technology, Shapingba, Chongqing 400054, China
在石油开采的过程中,通过检测油井动液面深度,能够科学地了解油井供应能力,确定抽油泵的沉没深度、油层压力,分析能量衰减的异常原因等,从而合理安排采油工艺,使油井产油率最大化。而目前油井动液面深度检测方法往往存在检测精度不高等问题。因此,如何精确地进行油井动液面深度检测就成为了石油工作者和其他科技人员致力解决的问题。
随着现代油田科技的不断进步,油井动液面检测技术得到了很大的发展。目前,比较成熟的传统油井动液面深度检测方法可分为:浮筒法[1],工艺操作简便,数据直观,但不能在带有压力的环空油井中测试;压力计探测法[2],适用于一切油水井,但须保证压力计停点至少有3个点在液面以下,施工周期长;示功图法[3-4],它可进行连续计算,但受到惯性、振动及摩擦载荷的影响;物质平衡法[5],通过测试环空中的气体排量折算出油井动液面,但折算过程并不精确;声波法[6],它不用将仪器下入井中,施工方便,但当井下液面较深或有泡沫层等因素时,检测精确大大降低。这几种方法模型简单,都需要在一定的条件下进行检测。在长期探索的过程中,又陆续提出了一些改进方法,如孟开元等[7]对抽油井液位回音曲线特性分析,设计了回音信号检测电路,利用计算机提取回音信号中的特性脉冲来计算液位值;McCoy J N等[8]提出一种基于声音传播的油井动液面检测方法;田学隆等[9]提出基于泡沫液的光电传感器液位检测方法;Terzic E等[10]提出基于电容式传感器的神经网络动液面检测方法;Sengupta D等[11]提出基于静水压力FBG传感的液位检测方法。这些方法能实时监控跟踪油井动液面的变化,但往往油井环形空间狭窄,液面偏深,声波信号衰减幅度大,最终难以进行精确检测。上述方法中遇到的问题,必然会影响到油井动液面深度检测的精度,也是制约油井供应能力、油田科学发展的瓶颈。
本研究发现生活中一个有趣的现象:乐师在吹奏长号时,通过拉动套管发出不同音高的声音。长号又称拉管,在拉动套管时会改变所连入的乐管长度,进而改变管内空气的固有频率,空气柱振动特点是管子越长,则频率越低,反之亦然。这意味着管乐器声乐频率可以反映乐管的长度。而油井套管与长号的管筒有着相似的形状(如图 1),那么上述现象是否暗示着可以通过测油井管柱声场固有频率来测油井动液面深度呢?
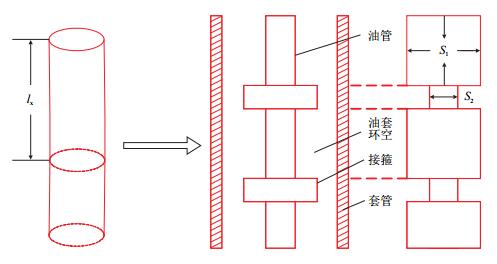 |
| 图1 长号与油管结构示意图 Fig. 1 Diagram of trumpet and oil wells |
通过分析相关文献,范理等[12]指出在管中气体、温度、压力等条件一定时,谐振管长度和管两端阻抗是影响谐振频率的最主要因素,并提出了运用声压模拟法和驻波最小点法计算声谐振管的谐振频率。宫瑞婷等[13]对声制冷机中均匀声共振管声场进行了研究,指出在共振时声波在管的刚性端面处的声压最大。汤珂等[14]研究了热声驱动器谐振频率的影响因素,指出一端封闭一端开口谐振管的驻波热声驱动器,其谐振频率与谐振管长成反比。赵辉等[15]介绍了运用管内音频信号共振的原理对管件长度进行测量的方法,并进行了相应的理论分析。在不考虑声音信号的衰减、声速变化、泡沫油等影响的情况下,油井可简化为管道模型。由此可知,油井动液面深度与管内声场固有频率之间必然存在一定的关系。
为此,本文提出一种基于管柱声场模型的油井动液面深度检测方法。首先,借助管道声学理论对典型的管道结构进行分析;然后,通过频率共振法得到管内液面深度;最后,通过实验装置对此进行验证。该方法拟为长期以来油井动液面深度检测存在的问题提供一种新的途径,从而有助于解决石油开采中迫切需要解决的关键科技问题。
1 典型管柱的管内声场特性设有一平面声波在一根有限长且截面积均匀的管中传播,管的截面积为S。若管末端有一任意声学负载,它的表面法向声阻抗为Za,则一部分声波要受到反射,另一部分要被负载所吸收。因此,管中的原始平面行波声场会受到负载的影响。通常的阻抗声管如图 2所示。
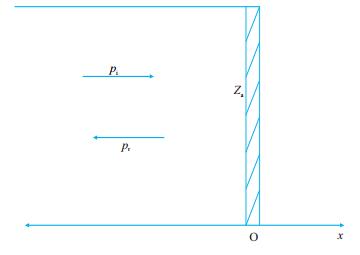 |
| 图2 声管示意图 Fig. 2 Schematic of acoustic tube |
它是一根圆柱形的刚性金属管,一端开口,一端封闭。在管内建立直角坐标系,取原点在管末端的负载处,设入射波与反射波的形式分别为
| $ {p_{\rm{i}}} = {p_{{\rm{ai}}}}{{\rm{e}}^{j(\omega t - kx)}} $ | (1) |
| $ {p_{\rm{r}}} = {p_{{\rm{ar}}}}{{\rm{e}}^{j(\omega t + kx)}} $ | (2) |
反射波声压par是由管端的声学负载引起的,它与入射波声压pai之间不仅大小不同,还可能存在相位差,一般可表示为
| $ \frac{{{p_{{\rm{ar}}}}}}{{{p_{{\rm{ai}}}}}} = {r_{\rm{p}}} = |{r_{\rm{p}}}|{{\rm{e}}^{j\sigma \pi }} $ | (3) |
由式(1),式(2)可得管中的总声压为
| $ p = {p_{\rm{i}}} + {p_{\rm{r}}} = {p_{{\rm{ai}}}}\left[{{e^{-jkx}} + |{r_{\rm{p}}}|{{\rm{e}}^{j(kx + \sigma \pi )}}} \right]{{\rm{e}}^{j\omega t}} = |{p_{\rm{a}}}|{{\rm{e}}^{j(\omega t + \phi )}} $ | (4) |
其中
| $ |{p_{\rm{a}}}| = {p_{{\rm{ai}}}}\left| {\sqrt {1 + |{r_{\rm{p}}}{|^2} + 2|{r_{\rm{p}}}|\cos 2k\left( {x + \sigma \frac{\lambda }{4}} \right)} } \right| $ | (5) |
当2k(x+σλ/4)=±(2n+1)π(n=0, 1, 2, …)时,p有极小值;当2k(x+σλ/4)=2nπ(n=0, 1, 2, …)时,p有极大值。若声负载是一刚性反射面,将入射声波全部反射,则|rp|=1,|pa|=2pai|coskx|,此时管中出现了纯粹的驻波。
2 管内空气柱共振原理对于图 2所示的圆柱形刚性管,设管道内径为d,若d/λ < 0.5,管道可近似看作一维系统,管内只有沿管长传播的一维平面波[16-17]。设声源在管口,管长为l。入射波与反射波的质点速度分别为
| $ \begin{array}{l} {v_{\rm{i}}} = {v_{{\rm{ai}}}}{{\rm{e}}^{j(\omega t-kx)}} \end{array} $ | (6) |
| $ {v_{\rm{r}}} = {v_{{\rm{ar}}}}{{\rm{e}}^{j(\omega t + kx)}} $ | (7) |
其中:vai=pai/ρ0c0,var=-par/ρ0c0。ρ0c0为媒质的特性阻抗。
管中任意处质点速度为
| $ v = {v_{\rm{i}}} + {v_{\rm{r}}} = \frac{{{p_{\rm{i}}}}}{{\rho_0{c_0}}}-\frac{{{p_{\rm{r}}}}}{{\rho_0{c_0}}} $ | (8) |
则管中任一点的声阻抗率为
| $ {Z_{\rm{s}}} = \frac{p}{v} = \rho_0{c_0}\frac{{{p_{{\rm{ai}}}}{e^{-jkx}} + {p_{{\rm{ar}}}}{e^{jkx}}}}{{{p_{{\rm{ai}}}}{e^{-jkx}}-{p_{{\rm{ar}}}}{e^{jkx}}}} $ | (9) |
设管子末端l处的声阻抗为Zal,声阻抗率为Zsl,则
| $ {Z_{{\rm{sl}}}} = \rho_0{c_0}\frac{{{p_{{\rm{ai}}}}{e^{-jkl}} + {p_{{\rm{ar}}}}{e^{jkl}}}}{{{p_{{\rm{ai}}}}{e^{-jkl}}-{p_{{\rm{ar}}}}{e^{jkl}}}} $ | (10) |
设管口输入声阻抗为Za0,声阻抗率为Zs0,则由以上可得管口声阻抗率为
| $ {Z_{{\rm{s0}}}} = {\rho _0}{c_0}\frac{{{Z_{{\rm{sl}}}} + j{\rho _0}{c_0}\tan (kl)}}{{{\rho _0}{c_0} + {jZ_{{\rm{sl}}}}\tan (kl)}} $ | (11) |
则管口声阻抗为
| $ {Z_{{\rm{a0}}}} = \frac{{{\rho _0}{c_0}}}{S}\frac{{{Z_{{\rm{al}}}} + j\frac{{{\rho _0}{c_0}}}{S}\tan (kl)}}{{\frac{{{\rho _0}{c_0}}}{S} + j{Z_{{\rm{al}}}}\tan (kl)}} $ | (12) |
其中:波数k=2π/λ=2πf/c。
若管的末端刚性封闭,即Zal→∞,则
| $ {Z_{{\rm{a0}}}} \approx \frac{{{\rho _0}{c_0}}}{S}\frac{1}{{j\tan (kl)}} =-j\frac{{{\rho _0}{c_0}}}{S}\cot (kl) $ | (13) |
当kl=(2n-1)π/2或kl=nπ时,有
| $ {Z_{{\rm{a0}}}}\left\{ \begin{array}{l} 0, kl = (2n-1)\frac{\pi }{2}\;\;\;n = 1, 2, 3, \cdots \\ \infty, kl = n\pi \;\;\;\;n = 1, 2, 3, \cdots \end{array} \right. $ | (14) |
即当kl=(2n-1)π/2(n=1, 2, 3…)时,Za0=0,此时管将发生共振。据波数定义知,此时,空气柱的共振频率为
| $ {f_n} = \frac{{(2n-1)c}}{{4{l_{\rm{p}}}}}, \;n = 1, 2, 3, \cdots $ | (15) |
其中lp为空气柱长度。考虑管端校正,则
| $ {l_{\rm{p}}} = l + 0.3d $ | (16) |
若将管子垂直竖立,通过向管中注水,调节注水深度,则液面到管口的高度lx为
| $ {l_x} = \frac{{(2n-1)c}}{{4{f_n}}}-0.3d, \;n = 1, 2, 3, \cdots $ | (17) |
由以上原理可知,只要能得到管内空气柱的共振频率,即管内声场的固有频率,就能求出管内液面深度。因此,如何精确检测共振频率是本项研究的关键。本实验通过搭建相应的软件和硬件平台,采用频率法,即快速傅立叶变换(FFT),精确得出共振频率值。
本文利用自制的实验装置,实验所用器材包括直流稳压电源、白噪声信号发生器、滤波器、功率放大器、扬声器、共振管、驻极式话筒、A/D采样卡、示波器、计算机等。实验流程如图 3所示。
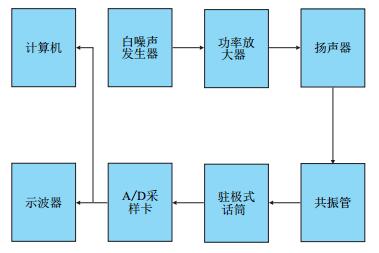 |
| 图3 实验流程图 Fig. 3 Flow diagram of experiment |
首先通过计算机控制发出白噪声信号,进行滤波处理,通过功率放大器后驱动扬声器作为驱动声源,信号传入管道,然后通过驻极式话筒得到输出信号,再经A/D采样卡将模拟信号数字化,采样频率设为2 000 Hz,采样精度为0.98 Hz,最后输送至计算机和示波器,进行频谱检测分析,获得管中空气柱的共振频率。最后,通过式(17)计算得到管内液面深度。
3.2 实验过程与结果分析实验管长为1~280 mm,内径100 mm。实验过程按照图 3所示,具体实验步骤如下:
(1) 用示波器测得直流稳压电源电压为8.8 V,并将它供给驻极式话筒。
(2) 测试话筒的输出端电压。若直流电压较高,则在话筒输出端串联一个100 pF的电容滤去直流成分,此时示波器上电压显示为0。向驻极式话筒发出声音时,示波器上有明显的波形。
(3) 在计算机虚拟信号发生器上设置相应参数,设置声音信号为白噪声,上限频率为800 Hz,下限频率为20 Hz,选中频率平均,滤波等参数。
(4) 连接白噪声发生器到驻极式话筒的部分实验电路,接通电源,调节话筒上的增益旋钮,使其输出端交流电压最大值在5 V以内,以确保A/D采样卡安全工作。
(5) 按图 3所示连接实验装置,接通电源,开始实验。
为验证本文提出的油井动液面深度检测方法,设计了两种不同的实验手段来验证方法的可行性。
(1) 在共振管内上下移动驻极式话筒的探头。在计算机上检测管内声压的幅值分布及频率值,探头在管内某处时,实验结果如图 4和图 5所示。
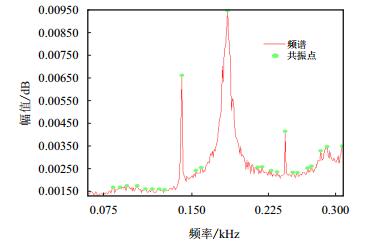 |
| 图4 探头距离管口某位置处的信号频域分布图 Fig. 4 Distribution of the signal frequency |
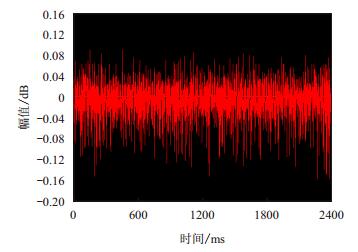 |
| 图5 探头距离管口某位置处的信号时域分布图 Fig. 5 Distribution of the signal time-domain |
由图 4知,实验所得管内空气柱的共振频率为195 Hz,令n=2,则lx=3c/4fn-0.3d=1 277.7 mm,理论值为1 280 mm,相对误差为0.18%。通过多次实验发现,当n=1时,管内的声音信号规律并不能明显体现。为此,本实验观测并分析管内声场的二阶信号。
随着探头探入管内深度h的不同,声压幅值A如图 6所示。
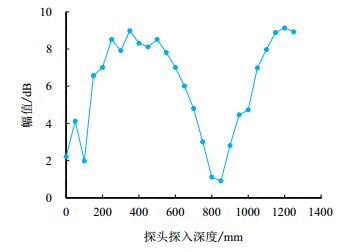 |
| 图6 声压幅值随深度变化曲线 Fig. 6 Relationship between sound pressure amplitude and depth |
图 6给出了管内声场固有频率为195 Hz时声压的幅值分布,通过图 6和表 1可知,在不同位置处,管内声压振幅不同,其最小值与最大值之比约为0.09,但并不为0。这可能是由驻极式话筒对声场的影响造成的。以上实验表明,管柱开口处近似为波节,封闭端近似为波腹,声压振幅的分布近似一段驻波。
| 表1 不同深度的声压幅值表 Table 1 Different depth of sound pressure amplitude |
(2) 向管内注水,观察并记录不同液面深度时,管内空气柱的共振频率f。通过共振频率,计算液面到管口的深度lx,并与实际值l0进行比较。由于管腔模型需满足d/λ < 0.5,实验时管子不能太短,本实验管内空气柱长度在700 mm以上。
表 2和图 7给出了管内液面深度测试值与实际值的比较。据表 2可得,在本实验中,随着管件长度的增加,误差没有明显变化,波动较小且相对误差E均在2%以内。由图 7和表 2可知,本文提出的动液面检测方法得到的管内液面深度与实际液面深度间误差较小。实验结果表明,通过管内空气柱的共振,建立油井动液面深度与管内声场固有频率关系的方法能较为精确地检测到管内液面深度,起到了很好的测量效果。
| 表2 不同深度实验测量数据表 Table 2 Different depth of measurement data |
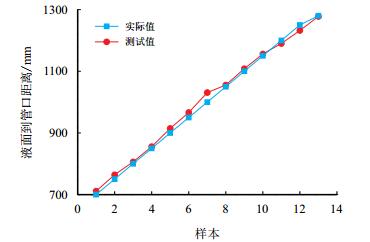 |
| 图7 管内液面深度测试值与实际值比较 Fig. 7 Comparison between the measured value and the actual value |
本文提出一种基于管柱声场模型的油井动液面深度检测方法,通过管柱测试实验表明,该方法能够检测管柱声场的固有频率,从而较精确地获得管内液面深度,为油井动液面深度检测提供了一种新的研究途径。在实际油井中,往往存在以下问题:
(1) 由于声波在套管内气体中传播时能量衰减剧烈,当传播较长距离到达液面时,被液面反射的声波幅值可能较小,现在油田普遍使用的气枪发射脉冲波的方式显然不能形成驻波,无法达到共振,本研究将在后续实验中采用气流调制喇叭发出连续波,能有效解决声波在井下传播时能量不足的问题。
(2) 随着管柱长度的增加,管内空气柱的共振频率降低,受扬声器频率限制,通常的扬声器无法满足油井液面检测需要,同样,气流调制喇叭可以满足此低频要求。
(3) 由于井内温度、湿度及液面蒸汽压力等的影响,液面上部空气密度随深度发生变化,导致声音在管内传播速度在不同深处并不相同,对此,将采用取平均值的方法,并适当引入修正。
(4) 泡沫油对声音信号的精确检测也有一定的影响。
以上各种因素,可能会对油井液面检测精度产生显著的影响。为此,下一步将重点研究管内温度、湿度、压力以及泡沫等因素对声速以及模态分布的影响和如何改进发生装置以满足长管实验要求。
| [1] |
陈殿房, 韩祥立, 杨晶. 油井液面探测方法探讨[J].
油气井测试, 2008, 17 (2) : 60 –61.
Chen Dianfang, Han Xiangli, Yang Jing. Discuss on survey method for liquid level of oil well[J]. Well Testing, 2008, 17 (2) : 60 –61. |
| [2] |
张洪. 压力计探测液面法探讨[J].
油气井测试, 2003, 12 (5) : 49 –50.
Zhang Hong. Discussion of detecting fluid level by pressure gauge[J]. Well Testing, 2003, 12 (5) : 49 –50. |
| [3] |
张向阳, 李凡磊, 陶剑清, 等. 功图液面自动监测技术在江苏油田的应用[J].
中外能源, 2008, 13 (4) : 66 –69.
Zhang Xiangyang, Li Fanlei, Tao Jianqing, et al. Application of automatic wireless testing technique of indicator diagram and well liquid level in Jiangsu Oilfield[J]. SinoGlobal Energy, 2008, 13 (4) : 66 –69. |
| [4] |
张胜利, 罗毅, 吴赞美, 等. 抽油机井示功图法计算动液面的修正算法[J].
石油钻采工艺, 2011, 33 (6) : 122 –124.
Zhang Shengli, Luo Yi, Wu Zanmei, et al. Corrected algorithm for calculating dynamic fluid level with indicator diagram for rob-pumped well[J]. Oil Drilling & Production Technology, 2011, 33 (6) : 122 –124. |
| [5] |
武德宁, 刘平良, 张少标. 物质平衡法测油井液面[J].
油气井测试, 2003, 12 (1) : 31 –32.
Wu Dening, Liu Pingliang, Zhang Shaobiao. To test the liquid level of a pump well by a material balance method[J]. Well Testing, 2003, 12 (1) : 31 –32. |
| [6] | Budenkov G A, Pryakhin A V, Strizhak V A. Device for detecting the liquid level in the annular space[J]. Russian Journal of Nondestructive Testing, 2003, 39 (9) : 654 –656. DOI:10.1023/B:RUNT.0000019715.00507.35 |
| [7] |
孟开元, 庄贵林, 曹庆年. 从抽油井液位回音信号中提取液位值的方法[J].
西安石油学院学报:自然科学版, 2001, 16 (4) : 66 –67, 84.
Meng Kaiyuan, Zhuang Guilin, Cao Qingnian. The method of extracting the liquid level value of a pumping well from the echo signal of liquid surface[J]. Journal of Xi'an Petroleum Institute:Natural Science Edition, 2001, 16 (4) : 66 –67, 84. |
| [8] | Mccoy J N, Rowlan O L. Acoustic liquid level testing of gas wells[C]. SPE 120643, 2009. |
| [9] |
田学隆, 林芳钦. 基于光电传感器的液位检测方法与装置[J].
传感器与微系统, 2009, 28 (10) : 73 –74, 78.
Tian Xuelong, Lin Fangqin. Liquid level detecting method and equipment based on optoelectronic sensor[J]. Transducer and Microsystem Technologies, 2009, 28 (10) : 73 –74, 78. |
| [10] | Terzic E, Nagarajah C R, Alamgir M. Capacitive sensorbased fluid level measurement in a dynamic environment using neural network[J]. Engineering Applications of Artificial Intelligence, 2010, 23 (4) : 614 –619. DOI:10.1016/j.engappai.2009.09.014 |
| [11] | Sengupta D, Sai Shankar M, Saidi Reddy P, et al. Sensing of hydrostatic pressure using FBG sensor for liquid level measurement[J]. Microwave and Optical Technology Letters, 2012, 54 (7) : 1679 –1683. |
| [12] |
范理, 王本仁, 金滔, 等. 谐振管谐振频率计算方法的研究[J].
声学学报, 2005, 30 (5) : 409 –414.
Fan Li, Wang Benren, Jin Tao, et al. Study on computing of resonance frequeney of resonance pipes[J]. Acta Acustica, 2005, 30 (5) : 409 –414. |
| [13] |
宫瑞婷, 余丽芳. 声制冷机中均匀声共振管声场的研究[J].
北京建筑工程学院学报, 2002, 18 (1) : 83 –86.
Gong Ruiting, Yu Lifang. The research of acoustic wave in equal-section resonance pipe of a thermoacoustic refrigerator[J]. Journal of Beijing Institute of Civil Engineering and Architecture, 2002, 18 (1) : 83 –86. |
| [14] |
汤珂, 陈国邦, 黄永华, 等. 热声驱动器谐振频率影响因素分析[J].
低温与超导, 2003, 31 (1) : 23 –26, 30.
Tang Ke, Chen Guobang, Huang Yonghua, et al. Analysis of factors influencing resonance frequency of the thermoacoustic engine[J]. Cryogenics and Superconductivity, 2003, 31 (1) : 23 –26, 30. |
| [15] |
赵辉, 丁雷, 杨培敏. 利用声共振测量管件长度的研究[J].
宇航计测技术, 1998, 18 (6) : 1 –8.
Zhao Hui, Ding Lei, Yang Peimin. The research on measurement of pipe length by means of acoustic resonance[J]. Journal of Astronaueic Metrology and Measurement, 1998, 18 (6) : 1 –8. |
| [16] | Peat K S. Acoustic impedance at the interface between a plain and a perforated pipe[J]. Journal of Sound and Vibration, 2010, 329 (14) : 2884 –2894. DOI:10.1016/j.jsv.2010.01.037 |
| [17] |
郭天葵, 钟会林, 周述苍, 等. 基于声共振原理的管道长度测量仪[J].
物理实验, 2012, 32 (5) : 28 –30.
Guo Tiankui, Zhong Huilin, Zhou Shucang, et al. Pipeline length measurement based on sound resonance[J]. Physics Experimentation, 2012, 32 (5) : 28 –30. |
 2015, Vol. 37
2015, Vol. 37


