2. 中国科学院大学, 北京 石景山 100049;
3. 西南石油大学地球科学与技术学院, 四川 成都 610500
2. University of Chinese Academy of Sciences, Shijingshan, Beijing 100049, China;
3. School of Geoscience and Technology, Southwest Petroleum University, Chengdu, Sichuan 610500, China
油水井套管损坏(以下简称套损)是油田开发中遇到的一大技术难题,而且,随着开发时间延长,套损将越来越严重。套损机理复杂,影响因素多,为攻克这一难题,国内外学者从地质、工程等不同角度对套管损坏机理和影响因素进行了研究。
陈天愚、刘殿魁研究了套损由于地层倾角、地层压力等变化而受到影响;后来又引入了摩擦元进行模拟且考虑了岩石单元的非线性特性,并对地层压力、浸水域位置、浸水域大小和泥岩水化程度进行了
分析[1-2]。练章华等分别建立了岩石、水泥环、套管互相作用的黏弹塑性及弹塑性有限元力学模型,并用复杂力学系统进行了计算机仿真研究[3-4];李军、陈勉等建立了套管-水泥环-井壁围岩组合体的力学模型,对其进行弹塑性分析,但将地应力看成是均匀的;后来又对复杂地应力下的套损问题进行了研究[5-6]。刘建军等首先给出了流固耦合的数学力学模型,借助有限元分析得到了套管-水泥环-地层组合体系应力场的动态变化规律[7]。
以上研究对套管-水泥环-围岩的受力分析起到了很大的理论指导意义,但大都集中在给定注水井井底流压,对套管、水泥环、围岩的受力分析,且很少考虑流固耦合作用。套损通常是一个缓慢的过程,是注采诱发地应力场在井眼附近导致应力集中的结果。油藏渗流场的变化,不但可以使储层岩体的物理力学参数发生变化,还将导致储层有效应力发生改变,进而导致井眼附近应力发生变化,这一系列动态变化必将导致套管受力状态发生改变。因此,考虑渗流-应力耦合作用,根据单因素理论对套管径向挤压力进行分析将使计算结果更符合实际。
1 流固耦合的数学力学模型 1.1 渗流场的数学模型假设计入源汇项,若单位体积注出(或采入)的质量流量记为q,则储层岩石介质中单相流体流固耦合渗流场的数学表达式为[8]
| $ \begin{array}{*{20}{l}} {\frac{\partial }{{\partial x}}\left( {\frac{{\rho K}}{\eta }\frac{{\partial p}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {\frac{{\rho K}}{\eta }\frac{{\partial p}}{{\partial y}}} \right) + \frac{\partial }{{\partial z}}\left( {\frac{{\rho K}}{\eta }\frac{{\partial p}}{{\partial z}}} \right) + }\\ {\phi {\rho _0}{C_{\rm{f}}}\frac{{\partial p}}{{\partial t}} + \rho \frac{{1 - {\phi _0}}}{{{{\left( {1 + {\varepsilon _{\rm{v}}}} \right)}^2}}}\frac{{\partial {\varepsilon _{\rm{v}}}}}{{\partial t}} + q = 0} \end{array} $ | (1) |
式中:
ρ-流体密度,kg/m3;
K-储层介质渗透系数,m/s;
η-流体黏度系数,Pa·s;
ϕ-储层介质孔隙度,无因次;
ϕ0-初始孔隙度,无因次;
t-时间,s;
Cf-流体的压缩系数,无因次;
p-流体压强,Pa;
ρ0-流体初始密度,kg/m3;
εv-体积应变,无因次,且εv=εx+εy+εz;
εx, εy, εz-x,y,z方向的正应变,无因次。
1.2 应力场数学模型 1.2.1 平衡微分方程平衡微分方程的数学表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial {\sigma _x}}}{{\partial x}} + \frac{{\partial {\tau _{yx}}}}{{\partial y}} + \frac{{\partial {\tau _{zx}}}}{{\partial z}} - {f_x} = 0}\\ {\frac{{\partial {\sigma _y}}}{{\partial y}} + \frac{{\partial {\tau _{zy}}}}{{\partial z}} + \frac{{\partial {\tau _{xy}}}}{{\partial x}} - {f_y} = 0}\\ {\frac{{\partial {\sigma _z}}}{{\partial z}} + \frac{{\partial {\tau _{xz}}}}{{\partial x}} + \frac{{\partial {\tau _{yz}}}}{{\partial y}} - {f_z} = 0} \end{array}} \right. $ | (2) |
式中:
σx,σy,σz-x、y、z方向的正应力,Pa;
τxy,τyz,τzx-x、y、z方向的切应力,Pa;
fx,fy,fz-x、y、z方向的体力分量,Pa;
α-系数,a∈[0, 1]。
1.2.2 几何方程对于三维问题,几何方程的数学表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {{\varepsilon _x} = \frac{{\partial u}}{{\partial x}}, {\varepsilon _y} = \frac{{\partial v}}{{\partial y}}, {\varepsilon _z} = \frac{{\partial w}}{{\partial z}}, }\\ {{\gamma _{xy}} = \frac{{\partial v}}{{\partial x}} + \frac{{\partial u}}{{\partial y}}, {\gamma _{yz}} = \frac{{\partial w}}{{\partial y}} + \frac{{\partial v}}{{\partial z}}, }\\ {{\gamma _{zx}} = \frac{{\partial u}}{{\partial z}} + \frac{{\partial w}}{{\partial x}}} \end{array}} \right. $ | (3) |
式中:
γxy,γyz,γzx-x,y,z方向的切应变,无因次;
u,v,w-位移,m。
1.2.3 本构方程 1.2.3.1 弹性本构方程对于弹性问题,应力应变的关系可用数学表达式表示为
| $ \left\{ \begin{array}{l} {\varepsilon _x} = \frac{1}{E}\left[{{\sigma _x}-\mu \left( {{\sigma _y} + {\sigma _z}} \right)} \right]\\ {\varepsilon _y} = \frac{1}{E}\left[{{\sigma _y}-\mu \left( {{\sigma _x} + {\sigma _z}} \right)} \right]\\ {\gamma _{xy}} = \frac{{2\left( {1 + \mu } \right)}}{E}{\tau _{xy}}\\ {\gamma _{yz}} = \frac{{2\left( {1 + \mu } \right)}}{E}{\tau _{yz}}\\ {\gamma _{xz}} = \frac{{2\left( {1 + \mu } \right)}}{E}{\tau _{xz}} \end{array} \right. $ | (4) |
式中:
E-弹性模量,Pa;
µ-泊松比,无因次。
研究发现,耦合场中储层岩石介质的变形特征不能用纯线弹性理论完全反映。因此,对于耦合场中储层介质的变形特征应该借助非线弹性理论或者弹塑性理论来表达。对于涉及非线弹性或者弹塑性问题的求解方法,可以利用分段线化处理方法。线化处理的思想为:在所有增量步内,把总应变增量写成塑性应变增量和弹性应变增量和的形式,其数学表达式为[8]
| $ \left\{ {{\rm{d}}\varepsilon } \right\} = \left\{ {{\rm{d}}{\varepsilon ^{\rm{e}}}} \right\} + \left\{ {{\rm{d}}{\varepsilon ^{\rm{p}}}} \right\} $ | (5) |
式中:dε,dεe,dεp-总应变、弹性应变和塑性应变,无因次。
1.3 渗流场与应力场耦合关系油田开发过程中,注水和采油作业会导致渗流场发生改变,孔隙压力不但可以使储层岩体的物理力学参数发生变化,还将导致储层有效应力发生改变,同时,应力场会反作用于渗流场,使流体压力及流动速度发生变化,从而使渗流场发生改变。孔隙介质在受到荷载作用或扰动后微观几何形状发生改变,骨架颗粒的重新排列导致孔隙介质的孔隙度和渗透性发生改变。在完全耦合分析中渗透系数不再是常量,而是一个变量,通常表示成应力、应变或者孔隙度的函数,而孔隙度又可以用应力或应变的函数表示,所以,渗透系数最终可以表示成应力和应变的函数[15]。
| $ K = {K_0}{\left[{\left( {\frac{1}{{{\phi _0}}}} \right){{\left( {1 + {\varepsilon _{\rm{v}}}} \right)}^3}-\left( {\frac{{1-{\phi _0}}}{{{\phi _0}}}} \right)\left( {{{\left( {1 + {\varepsilon _{\rm{v}}}} \right)}^{-\frac{1}{3}}}} \right)} \right]^3} $ | (6) |
式中:
K0-初始渗透系数,m/s。
1.4 边界条件与初始条件 1.4.1 渗流场的边界条件和初始条件为了求解现实中的具体问题,必须已知要求解问题的定解条件。参照文献[16-17]可知,定解条件有两类:边界条件和初始条件。
(1)边界条件
流体渗流计算的边界条件主要包括定压边界和定量边界两类。定压边界,即未知函数在边界上的数值已知,且可以随时间t改变,其数学表达式为
| $ p\left( {x, y, z} \right){|_{\left( {x, y, z} \right) \in \Gamma }} = {f_{\rm{p}}}\left( {x, y, z, t} \right) $ | (7) |
式中:
p(x, y, z)|(x, y, z)∈Γ-t时刻,边界上点(x, y, z)的压力,Pa;
fp(x, y, z, t)-t时刻,边界上压力的给定函数,Pa。
定量边界即未知函数在边界上的梯度已知,或边界上未知函数的梯度为已知的函数,其数学表达式为
| $ \frac{{\partial p}}{{\partial n}}{\rm{|}}\mathit\Gamma = {f_{\rm{p}}}\left( {x,y,z,t} \right) $ | (8) |
式中:
n-边界的法线方向。
(2)初始条件
求解油藏非稳定渗流问题,不仅需要边界条件,还需要求解问题的初始条件。初始条件主要为初始时刻流体的饱和度和压力分布,其数学表达式为[18]
| $ p(x, y, z, 0) = {p_0}(x, y, z) $ | (9) |
| $ S(x, y, z, 0) = {S_0}(x, y, z) $ | (10) |
应力场的边界条件大多为第一类边界条件,即组合体系的面力为已知,其数学表达式为[19-20]
| $ {\sigma _{ij}}{L_j} = {F_i}\left( {x, y, z} \right) $ | (11) |
式中:
Lj-边界的方向导数,j=1,2,3;
Fi(x, y, z)-面力分布函数,i=1,2,3。
应力场的第二类边界条件即为位移已知,其数学表达式为[21]
| $ {u_i} = {g_i}\left( {x, y, z} \right) $ | (12) |
式中:
gi(x, y, z)位移函数, i=1, 2, 3。
2 套管受力的单因素分析 2.1 数值模型建立针对某区块的套损情况,开展了理论模型研究。模型为一注一采模型。储层厚20 m,井距85 m,位于地下1 200 m,初始地层压力12 MPa。从地应力、壁厚、直径、渗透率、孔隙度、弹性模量、泊松比、注采压力等几个方面入手,分析它们对套管受力的影响。
图 1为单因素分析有限元模型网格。为更好地研究套管所受的径向挤压力,在套管局部采用柱坐标系进行计算,图 2为套管及局部柱坐标系网格。
 |
| 图1 单因素分析有限元网格图 Fig. 1 Single factor analysis of finite element mesh |
 |
| 图2 套管、水泥环及局部柱坐标系 Fig. 2 Local cylindrical coordinates of casing, cement annulus and formation |
套管、泥环、地层的部分力学参数如表 1所示。
| 表1 不同注水压力时各参数取值 Table 1 Parameters of core sample structured element models |
采用上述理论模型对注水压力进行定量研究,得出不同注水压力下套管的受力情况。其他参数保持不变,仅改变注水压力值,注水压力分别取13,15,17,19,30 MPa。套管径向挤压力随注水压力的变化曲线如图 3所示。
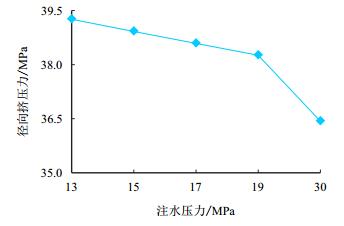 |
| 图3 不同注水压力时套管径向挤压力 Fig. 3 Radial compressive force curve with different water injection |
图 3表明,注水压力升高时,套管挤压力降低,由39.30 MPa降为36.50 MPa,与参考文献[23]给出的结论相似。表明注水压力升高时,地层有效应力减少,因而,套管所受挤压力总体上减少。
2.3.2 套管参数对套管受力的影响(1)套管弹性模量对其受力的影响
其他参数保持不变,弹性模量分别取8,9,10,11,12 GPa,套管所受径向挤压力随弹性模量的变化曲线如图 4所示。
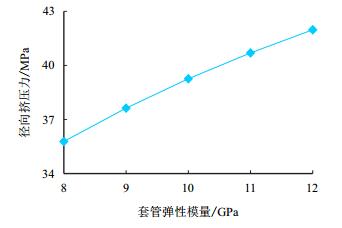 |
| 图4 套管不同弹性模量下径向挤压力曲线 Fig. 4 Radial compressive force curve with different elastic modulus of casing |
图 4表明,套管弹性模量不同,其受到的挤压力也不同。弹性模量越大,其所受挤压应力也越大,套管弹性模量由8 GPa增加到12 GPa,套管所受的径向挤压力由36.00 MPa变为42.00 MPa。因此,套管弹性模量并非越大越好,选用套管时,应选用弹性模量适中的套管,否则易造成太刚则折的后果。
(2)套管泊松比对其受力的影响
其他参数保持定值,套管泊松比分别取0.1,0.2,0.3,0.4,并对其在同一注采工况下的受力情况进行研究。套管径向挤压力随套管泊松比变化曲线如图 5所示。
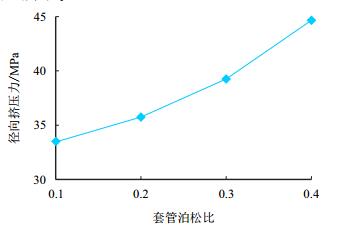 |
| 图5 不同套管泊松比下套管径向挤压力曲线 Fig. 5 Radial compressive force curve with different poisson′s ratio of casing |
由图 5可以看出,不同泊松比的套管应力不同。套管泊松比由0.1变化为0.4,套管径向挤压力由33.45 MPa增加为44.66 MPa。同时,实际情况下,泊松比与弹性模量是相关变化的,所以,在考虑泊松比的影响时,应当综合考虑弹性模量的变化。
(3)套管壁厚对套管受力的影响
其他参数保持不变,套管壁厚分别取7.12,8.12,9.12,10.12,11.12 mm。套管径向挤压力随套管壁厚的变化曲线如图 6所示。
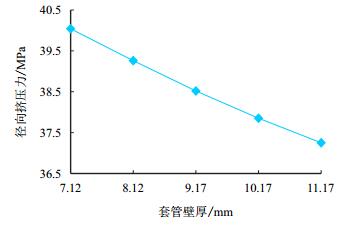 |
| 图6 不同套管壁厚下套管所受挤压力曲线 Fig. 6 Radial compressive force curve with different thicknesses of casing |
由图 6可以看出,套管径向挤压力随着套管壁厚的增加而减小,因此,适当增加套管壁厚能够减少套管受力。
(4)套管直径对套管受力的影响
其他参数保持不变,套管壁厚分别取104.00,110.00,116.00,122.00,128.00 mm。套管径向挤压力随套管直径的变化曲线如图 7所示。
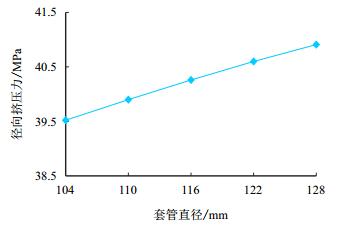 |
| 图7 不同套管直径下套管所受挤压力曲线 Fig. 7 Radial compressive force curve with different diameters of casing |
由图 7可以看出,套管直径越大,其所受到的挤压力也越大。套管壁直径由104 mm变为128 mm,所受挤压力由39.52 MPa变为40.91 MPa,变化较小。
2.3.3 地层参数对套管受力的影响(1)地层渗透率对套管受力的影响
其他参数保持不变,地层渗透率分别取127,327,527,727,927 mD,套管径向挤压力随地层渗透率的变化曲线如图 8所示。
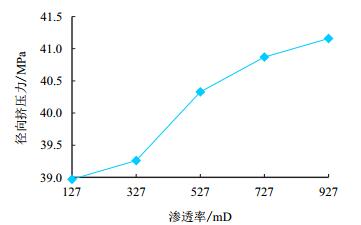 |
| 图8 不同地层渗透率下套管挤压力曲线 Fig. 8 Radial compressive force curve with different permeabilities of formation |
由图 8可以看出,地层渗透率越大,套管所受到的挤压力也越大。表明,渗透率越大,地层内部渗流场对套管的受力影响越明显。
(2)地层孔隙度对套管受力的影响
其他参数保持不变,地层孔隙度分别取0.09,0.29,0.49,0.69,套管径向挤压力随地层孔隙度的变化曲线如图 9所示。
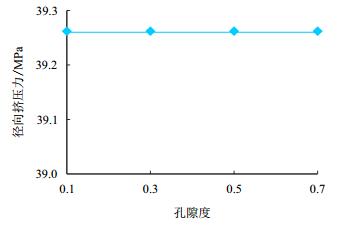 |
| 图9 不同地层孔隙度下套管挤压力曲线 Fig. 9 Radial compressive force curve with different porosities of formation |
由图 9可以看出,地层孔隙度不会对套管受力造成严重的影响。然而在实际地层中,孔隙度与其他各参数,如弹性模量、泊松比、渗透率等参数是有相关性的,所以在考虑孔隙度的影响时,还应该综合考虑其他参数的影响。
(3)地层泊松比对套管受力的影响
其他参数保持不变,地层泊松比分别取0.1,0.2,0.3,0.4,套管径向挤压力随套地层泊松比的变化曲线如图 10所示。
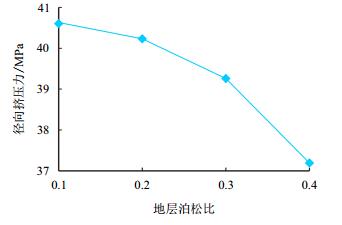 |
| 图10 不同地层泊松比下套管径向挤压力曲线 Fig. 10 Radial compressive force curve with different Poisson's ratio of formation |
由图 10可以看出,地层泊松比对套管受力亦有较大影响。地层泊松比越大,套管受力越小。当地层泊松比较大时,由于其纵向及横向变形之间的关联性差,当地层发生纵向变形时,其侧向变形相对较小,因而套管所受侧向挤压力也会相应减小。
(4)地层弹性模量对套管受力的影响
其他参数保持不变,地层弹性模量分别取8,9,10,11,12 GPa。套管径向挤压力随套管弹性模量的变化曲线如图 11所示。
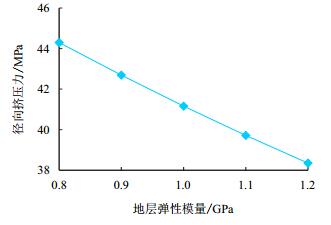 |
| 图11 不同地层弹性模量下套管所受径向力曲线 Fig. 11 Radial compressive force curve with different elastic modulus of formation |
图 11显示,地层弹性模量对套管有较大影响。表现为弹性模量越高,套管侧向挤压应力越小,与套管侧向挤压应力随套管弹性模量的变化趋势相反。地层弹性模量由8 GPa变化为12 GPa时,套管径向挤压力由44.3 MPa减小为38.35 MPa。
2.3.4 地应力对套管受力的影响研究了不同地应力时,注采作业下套管的受力情况。其他参数保持不变,地应力分别取20.00,30.00,40.00,50.00,60.00 MPa。套管径向挤压力随地应力的变化曲线如图 12所示。
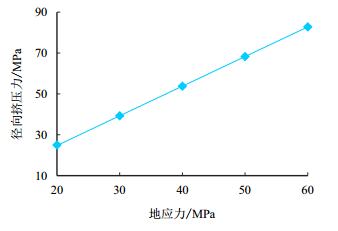 |
| 图12 不同地应力下套管径向挤压力曲线 Fig. 12 Radial compressive force curve with different crustal stress |
图 12显示,套管所受挤压力随地应力的增加而增加,几乎呈线性关系。地应力由20.00 MPa变化到60.00 MPa,套管径向挤压力由27.73 MPa升高到82.76 MPa,变化幅度较为明显,表明,地应力大小对套管挤压力影响明显。因此,在选用套管时,应当探明原地应力大小,根据地应力大小选取相应强度指标的套管。
3 结论(1)注水压力升高时,套管挤压力降低。
(2)弹性模量越大,其所受挤压应力也越大;在其他参数相同的情况下,不同泊松比的套管的应力情况基本上一致;具有较厚壁厚的套管所受到的挤压力比较小,因此,增加套管壁厚能够减少套管受力;套管直径越大,在壁厚不变的情况下,其所受到的挤压力也越大。
(3)地层渗透率越大,套管所受到的挤压力也越大;地层孔隙度单因素不会对套管受力造成严重的影响;地层泊松比对于套管受力亦有较大影响,地层泊松比越大,套管受力越小;地层弹性模量对套管有较大影响,表现为弹性模量越高,套管侧向挤压应力也越小。
(4)地应力与套管所受挤压图几乎是线性关系,直接影响到套管挤压图大小。
| [1] |
陈天愚, 刘殿魁. 套损问题影响因素分析[J].
哈尔滨工程大学学报, 2004, 25 (1) : 104 –107.
Chen Tianyu, Liu Diankui. Causes for damage to casing[J]. Journal of Harbin Engineering University, 2004, 25 (1) : 104 –107. |
| [2] |
陈天愚, 刘殿魁. 有限元方法计算套损问题[J].
哈尔滨工程大学学报, 2003, 24 (3) : 330 –333.
Chen Tianyu, Liu Diankui. Calculation of casing damage by finite element method[J]. Journal of Harbin Engineering University, 2003, 24 (3) : 330 –333. |
| [3] |
练章华, 张先普, 赵国珍, 等. 岩石、水泥环、套管互作用的粘弹塑性有限元力学模型[J].
西南石油学院学报, 1994, 16 (2) : 97 –103.
Lian Zhanghua, Zhang Xianpu, Zhao Guozhen, et al. Viscoelastic-plastic finite element mechanics models of interaetion of rock, cement ring and casing[J]. Journal of Southwestern Petroleum Institute, 1994, 16 (2) : 97 –103. |
| [4] |
练章华, 刘干唐, 董范, 等. 塑性流动地层套管破坏的有限元分析[J].
天然气工业, 2002, 22 (6) : 55 –57.
Lian Zhanghua, Liu Gantang, Dong Fan, et al. Finite element analysis of casing damage in plastic flow formation[J]. Natural Gas Industry, 2002, 22 (6) : 55 –57. |
| [5] |
李军, 陈勉, 张辉. 套管、水泥环及井壁围岩组合体的弹塑性分析[J].
石油学报, 2005, 26 (6) : 99 –103.
Li Jun, Chen Mian, ZhanG Hui. Elastic-plastic analysis of casing-concrete sheath-rock combination[J]. Acta Peirolei Sinica, 2005, 26 (6) : 99 –103. |
| [6] | 李军, 陈勉, 赵辉, 等. 复杂地应力下的石油套管损坏问题.岩石力学与石油工程研究进展[M]. 北京: 石油工业出版社, 2005 . |
| [7] | Liu Jianjun, Yu Xianbin. Stress analysis on the combination of casing-cement ring-surrounding rock considering fluid-solid coupling[J]. Electronic Journal of Geotechnical Engineering, 2012, 17 : 1863 –1873. |
| [8] | Liu Jianjun, Yu Xianbin, Zhao Jinzhou. Numerical simulation of geostress and pore pressure evolution around oil or water well under different injection-production ratio[J]. Mathematical Problems in Engineering, 2013 . |
| [9] | 周维垣. 高等岩石力学[M]. 北京: 中国水利水电出版社, 1986 . |
| [10] | 朱伯芳. 有限单元法原理与应用[M]. 北京: 中国水利水电出版社, 1988 . |
| [11] | 刘建军, 曾流芳, 纪佑军, 等. 热采井套管损坏力学机理及数值模拟[M]. 北京: 科学出版社, 2013 . |
| [12] | Yue Jiannan, Liu Jianjun. Numerical simulation of drainage process or sand cushion in saturated asphalt pavement[J]. Electronic Journal of Geotechnical Engineering, 2012, 17 (S1) : 3905 –3914. |
| [13] | Liu Jianjun, Song Rui, Zhao Jinzhou. Numerical simulation research on seepage mechanism in pore-scale deformable porous media[J]. Disaster Advances, 2013, 6 (S1) : 49 –58. |
| [14] | 纪佑军.渗流诱发套损机理及数值模拟研究[D].武汉:武汉工业学院, 2007. http://www.meeting.edu.cn/meeting/subject/paper!detail1.action?id=20756 |
| [15] | 陈卫忠, 伍国军, 贾善坡. ABAQUS在隧道及地下工程中的应用[M]. 北京: 中国水利水电出版社, 2010 . |
| [16] | 李培超.多孔介质流固耦合渗流数学模型研究[D].北京:中国科学院, 2001. http://mall.cnki.net/magazine/article/yslx200416033.htm |
| [17] | 周志军.低渗透储层流固耦合渗流理论及应用研究[D].大庆:大庆石油学院, 2003. http://cdmd.cnki.com.cn/article/cdmd-10220-2003112087.htm |
| [18] | 刘建军.裂缝性低渗透油藏流固耦合理论及工程应用[D].北京:中国科学院, 2001. http://www.cnki.com.cn/article/cjfdtotal-yslx200304026.htm |
| [19] |
黄小兰, 冒海军, 刘建军, 等. ANSYS软件在注水井套损预测中的应用[J].
岩石力学与工程学报, 2005, 24 (S1) : 5146 –5150.
Huang Xiaolan, Mao Haijun, Liu Jianjun, et al. Application of ansys in forecasting of water injection well casing damage[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24 (S1) : 5146 –5150. |
| [20] |
尹中民, 武强, 刘建军, 等. 注水井泄压对套管挤压力影响的数值模拟[J].
岩石力学与工程学报, 2004, 23 (14) : 2390 –2395.
Yin Zhongmin, Wu Qiang, Liu Jianjun, et al. Numerical simulation on effect of pressure relief of water injection well on casing squeeze pressure[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23 (14) : 2390 –2395. |
| [21] |
纪佑军, 刘建军, 程松林. 考虑流固耦合的隧道开挖数值模拟[J].
岩土力学, 2011, 32 (4) : 1229 –1233.
Ji Youjun, Liu Jianjun, Cheng Linsong. Numerical simulation of tunnel excavation considering fluid solid coupling[J]. Rock and Soil Mechanics, 2011, 32 (4) : 1229 –1233. |
| [22] | 黄小兰.渗流诱发油田套损机理研究与数值分析[D].北京:中国科学院, 2008. http://d.wanfangdata.com.cn/Thesis/Y1620464 |
| [23] |
纪佑军, 刘建军, 程林松, 等. 基于热-流-固耦合的热采井受力数值计算[J].
工程力学, 2011, 28 (3) : 224 –229.
Ji Youjun, Liu Jianjun, Cheng Linsong, et al. Numerical computation of pressure on the thermal recovery well based on thermal-hydro-mechanical coupling[J]. Engineering Mechanics, 2011, 28 (3) : 224 –229. |
| [24] |
李根生, 黄中伟, 牛继磊, 等. 地应力及射孔参数对水力压裂影响的研究进展[J].
石油大学学报:自然科学版, 2005, 29 (3) : 136 –142.
Li Gensheng, Huang Zhongwei, Niu Jilei, et al. Research advance of the influence of geostress and perforation parameters on hydraulic fracturing[J]. Journal of the University of Petroleum, China, 2005, 29 (3) : 136 –142. |
| [25] | 李志明, 张金珠. 地应力与油气勘探开发[M]. 北京: 石油工业出版社, 1997 . |
| [26] | 易浩.复杂地层套管损坏机理研究[D].成都:西南石油学院, 2005. http://cdmd.cnki.com.cn/article/cdmd-10615-2006012030.htm |
 2015, Vol. 37
2015, Vol. 37


