精确耦合模型多采用微元思想,将分支水平井分解为若干微元,引入井筒压降,通过井筒壁面处渗流与管流压力相等的原则建立由非线性方程组构成的耦合模型。通过迭代求解,获得各井筒微元段的流量和压力剖面,求解分支井产能。
Basquet R等[1]采用了微元的思想,将鱼骨分支井分成若干小段,逐段进行渗流和井筒流动的耦合,建立了鱼骨分支井的耦合模型。Wolfsteiner C等[2]基于Green函数,采用表皮系数和近井渗透率共同来体现储层非均质性,建立了适合于非均质储层的复杂结构井产能计算的耦合模型。Ouyang L B和Aziz K[3-4]结合其先前的井筒压降模型采用节点分析法建立了分支井的耦合模型。Tabatabaei M和Ghalambor A[5]建立了箱形、近井地带渗透率非均质储层渗流与考虑完井表皮系数、井筒压降、径向入流流态(层流与湍流)影响的分支井耦合模型。
中国,刘想平等[6]在单支水平井耦合模型研究成果基础上,推导给出了鱼骨型多分支井耦合模型并求解其产能,研究表明分支水平井更适合开发薄油藏,尤其是带有底水的薄油藏。黄世军等[7-8]基于井筒流体流动与管道流体流动的相似性建立了地层渗流与井筒压降的耦合模型。陈卫东等[9]通过Joshi稳态或Helmy-Wattenbarger拟稳态油藏渗流模型,引入Ouyang Liangbiao[4]井筒压降模型,并将其推广至多分支水平井模型。杨小松等[10]建立了鱼骨型多分支水平气井在常规储层中的耦合模型,分析了储层物性、井筒压降、分支井型结构等因素对产能的影响。2011年段永刚等[11-12]在其单支水平井耦合模型研究基础上,建立了分支水平井油藏与井筒耦合的不稳定流动数学模型。同年,安永生[13]研究了油藏各向异性对鱼骨分支水平井产能的影响。2012年张殿锋[14]运用不稳定渗流理论,并引入Novy井筒压降模型建立了储层渗流和井筒流动的耦合模型。上述学者研究过的分支水平井的耦合模型多采用井筒微元处理的方法,而本文着眼于对储层进行微元处理,将储层进行切片细分,提出了一类新的微元处理方法和手段,着眼于储层的细分方法相比于对分支井段的细分能够大大简化耦合方程的系数矩阵,减少计算量,节约计算成本。
1 物理模型 1.1 模型基本假设底水油藏不对称鱼骨分支水平井物理模型如图 1所示,储层上边界封闭、下边界为恒压的初始油水界面,储层厚度为h,井筒半径为rw,井筒距油水界面高度为zw,假设分支等长、等间距、两侧交错排列;各分支井段投入生产,主井筒不参与生产仅参与导流。θi表示分支i的方向与x轴的夹角;油、水相界面分明且互不相容,储层物性、流体性质均匀、各向同性,单相流体稳定渗流,油水黏度和密度为常数,不考虑毛管力作用。
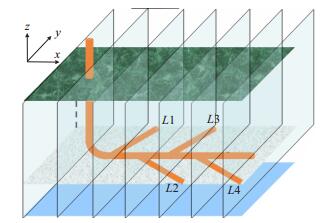 |
| 图1 底水油藏分支水平井示意图 Fig. 1 The multilateral horizontal well in the bottom water reservoir |
可对存在生产井段的储层进行切片微元细分,即沿着YZ平面将此模型的储层细分为k个等厚度的储层微元部分。储层细分的方案应根据分支井筒的长度来设计,细分的基本原则为:保持每一储层微元上的每一分支微元井段长度基本相等。对于本例微元细分如图 2所示,经过微元处理后本例将储层共分为18个微元部分,每一分支段在储层中的跨度为6个微元部分,每一储层微元中井筒微元段长度均为分支长度的1/6。
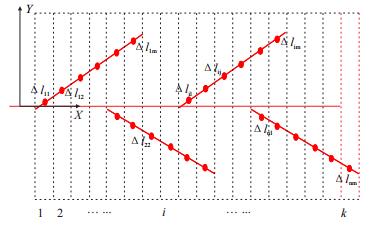 |
| 图2 底水油藏微元段划分XY平面示意图 Fig. 2 XY plane of micro-unit division in the bottom water reservoir |
经过上述对储层的细分切片微元处理后,每一储层微元切片上分布有1至2个投入生产的分支微元井段,如图 3a所示,由于底水油藏储层上边界封闭,下边界为恒压供给边界,因此当处于稳定渗流时,纵向YZ平面上的势差为提供流体渗流的动力,储层中压力干扰主要体现在YZ垂面,切片i与其他切片上的微元段在x方向上彼此干扰较小,可以忽略不计,此处理方法也是基于单支水平井底水油藏渗流模型推导过程中并不考虑各微元段在x方向上的干扰。由此针对储层微元上存在有1个、2个的生产微元段,可以分别运用单支、双支水平井产能公式表述各分支井筒微元段井底势差与流量之间的关系。
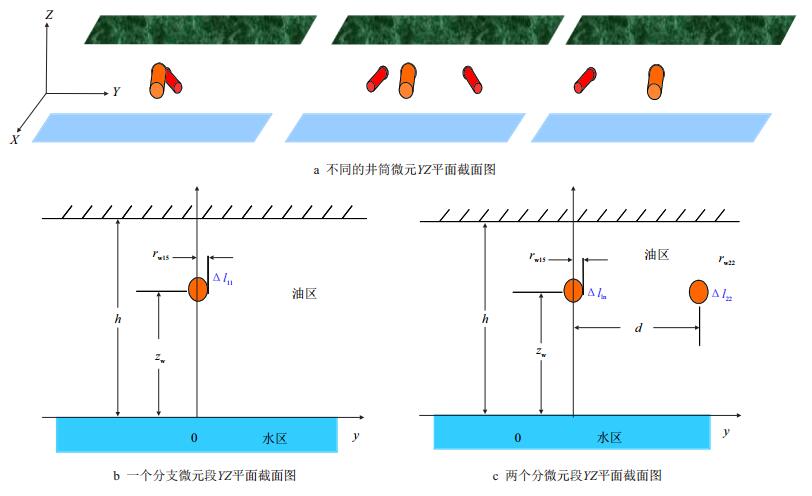 |
| 图3 底水油藏微元段划分YZ平面示意图 Fig. 3 YZ plane of micro-unit division in the bottom water reservoir |
针对存在1个分支微元段的切片,示意图如图 3b,根据YZ平面势叠加原理,采用文献[15]底水油藏单水平井产能公式,得到分支微元段井底势差与流量的关系式为
| $ {\mathit{\Phi} _e} - {\rm{ }}{\mathit{\Phi} _{{\rm{wf}}, ij}} = \frac{{{B_{\rm{o}}}{\mu _{\rm{o}}}}}{{2{\rm{\pi }}K}}\left( {\ln \frac{{4h}}{{{\rm{\pi }}{r_{\rm{w}}}}} + \ln \tan {\rm{ }}\frac{{{\rm{\pi }}{{\rm{z}}_{\rm{w}}}}}{{2h}}} \right){q_{{\rm{w}}, ij}} $ | (1) |
式中:
Φe-储层下边界处的势,MPa;
Φwf, ij井筒壁面处的势,MPa;
Bo-原油体积系数,无因次;
μo-储层原油黏度,mPa·s;
K-储层渗透率,mD;
h-储层厚度,m;
rw-井筒半径,m;
zw-井筒距离储层下边界的距离,m;
qw, ij-第i分支的第j微元的入流量,m3/s。
针对存在2个分支微元段的切片,示意图如图 3c,根据YZ平面内双井筒干扰问题,处理过程可采用文献[16]的方法,推导出两井相互干扰下的产能公式,得到该分支微元段井底势差与流量的关系式为
| $ \begin{array}{l} \mathit{\Phi} e - {\mathit{\Phi} _{{\rm{wf}}, ij}} = \frac{{{B_{\rm{o}}}{\mu _{\rm{o}}}}}{{2\pi K}}\left[{\left( {\ln \frac{{4h}}{{\pi {r_{\rm{w}}}}} + \ln \tan \frac{{\pi {{\rm{z}}_{\rm{w}}}}}{{2h}}} \right){q_{{\rm{w}}, ij}} + \frac{{{q_{{\rm{w}}, (i + 1)(j-4)}}}}{2}} \right.\\ \left. {\ln \frac{{\left( {{\rm{ch}}\frac{{{\rm{\pi }}{d_{ij}}}}{h} + \cos \frac{{{\rm{\pi }}{z_{\rm{w}}}}}{h}} \right)\left( {{\rm{ch}}\frac{{{\rm{\pi }}{d_{ij}}}}{h}-\cos \frac{{{\rm{\pi }}{r_{\rm{w}}}}}{{2h}}} \right)}}{{\left( {{\rm{ch}}\frac{{{\rm{\pi }}{d_{ij}}}}{h} + \cos \frac{{{\rm{\pi }}{r_{\rm{w}}}}}{{2h}}} \right)\left( {{\rm{ch}}\frac{{{\rm{\pi }}{d_{ij}}}}{h}-\cos \frac{{{\rm{\pi }}{z_{\rm{w}}}}}{h}} \right)}}} \right] \end{array} $ | (2) |
式中:
dij-第i分支的第j微元井段与处于同一储层微元切片上另一(本例为第i+1分支第j-4)微元井段的距离,m,其表达式为dij=
模型假设主井筒不生产,因此主井筒无加速度压降,主井筒各微元压降可表示为摩擦压降pwall, i和汇合压降pcon, i之和
| $ {p_{{\rm{wf}}, i}} - {p_{{\rm{wf}}, (i - 1)}} = \Delta {p_{{\rm{wall}}, i}} + \Delta {p_{{\rm{con}}, i}} $ | (3) |
把主井筒跟端处压力作为分支水平井的井底流压,则有
| $ {p_{{\rm{wf}}, 0}} = {p_{{\rm{wf}}}} $ | (4) |
对于不与分支结合部位的主井筒段其汇合压降pcon, i为0,但在分支与主支汇合处存在主分支汇合压降。对于汇合压降计算可采用文献[10}提供的汇合压降模型,其计算公式为
| $ \Delta {p_{{\rm{con}}, i}} = \frac{{{\rho _{\rm{o}}}}}{A}\left( {{q_{{\rm{w}}, i{\rm{ + 1}}}}{v_{{\rm{w}}, i{\rm{ + 1}}}}- {q_{{\rm{w}}, i}}{v_{{\rm{w}}, i}}- {q_{{\rm{w}}, j0}}{v_{{\rm{w}}, j0}}\cos {\theta _i}} \right) $ | (5) |
对于壁面摩擦压降计算公式如下
| $ \Delta {p_{{\rm{wall}}, i}} = \frac{{8{\rho _{\rm{o}}}{f_{{\rm{t, i}}}}}}{{{{\rm{\pi }}^2}{D^5}}}q_{{\rm{w}}, i}^2\Delta {L_i} $ | (6) |
主井筒由于不生产,其不同位置处截面流量为上游各分支井流量之和,数学表达式为
| $ {q_{{\rm{w}}, i}} = \sum\limits_{n = i}^N {{q_{{\rm{w}}, i0}}} $ | (7) |
式中:
pwf, i,pwf, (i-1)-主井筒第i,i-1微元段的井筒压力,MPa;
Δpwall, i-主井筒第i微元段的摩擦压降,Pa;
Δpcon, i主井筒第i微元段的汇合压降,Pa;
pwf, 0-主井筒跟端压力,MPa;
pwf-生产井井底流压,MPa;
ρo-原油密度,kg/m3;
A-主井筒的横截面积,m2;
qw, i-主井筒第i微元的主流流量,m3/s;
vw, i-主井筒第i微元的主流速度,m/s;
qw, j0-第j个分支跟端的总流量,m3/s;
qw, i0-第i个分支跟端的总流量,m3/s;
vw, j0-第j分支井筒的跟端流动速度,m/s;
θi-第i个分支与主井筒的夹角,(°);
ft, j-主井筒第i微元的壁面摩擦系数,计算方法参见文献[4];
D-主井筒的内径,m;
ΔLi-主井筒第i微元段长度,m。
3.2 分支井筒流动压降模型分支水平井第i分支的第j微元井段处的井筒压降可表示为摩擦压降Δpwall, ij、加速度压降Δpacc, ij、混合压降Δpmix, ij之和
| $ {p_{{\rm{wf}}, ij}} - {p_{{\rm{wf}}, i(j - 1)}} = \Delta {p_{{\rm{wall}}, ij}} + \Delta {p_{{\rm{acc}}, ij}} + \Delta {p_{{\rm{mix}}, ij}} $ | (8) |
其中各分支井筒跟端的压力等于分支井筒与主井筒交汇处的井筒压力
| $ {p_{{\rm{wf}}, i0}} = {p_{{\rm{wf}}, j}} $ | (9) |
壁面摩擦压降、加速度压降、混合压降计算式分别如式(10)~(12)
| $ \Delta {p_{{\rm{wall}}, ij}} = \frac{{8\rho {f_{{\rm{t}}, ij}}}}{{{{\rm{\pi }}^2}D_i^5}}q_{{\rm{w}}, ij}^2\Delta {l_{ij}} $ | (10) |
| $ \Delta {p_{{\rm{acc}}, ij}} = \frac{{32\rho {q_{{\rm{ws}}, ij}}}}{{{{\rm{\pi }}^2}D_i^4}}{q_{{\rm{w}}, ij}}{\rm{ }}\Delta {l_{ij}} $ | (11) |
| $ \Delta {p_{{\rm{mix}}, ij}} = \frac{{8\rho {q_{{\rm{ws}}, ij}}}}{{{{\rm{\pi }}^2}D_i^4}}{q_{{\rm{w}}, ij}}\Delta {l_{ij}} $ | (12) |
其中各分支井筒不同位置处截面流量为上游各分支微元段的流量之和
| $ {q_{{\rm{w}}, ij}} = \sum\limits_{m = j}^{{M_i}} {({q_{{\rm{ws}}, im}}} \Delta {l_{im}}) $ | (13) |
Δpwall, ij-第i分支的第j微元段井筒摩擦压降,Pa;
Δpacc, ij-第i分支的第j微元段井筒加速度压降,Pa;
Δpmix, ij-第i分支的第j微元段井筒混合压降,Pa;
pwf, i0-第i分支井筒的跟端压力,MPa;
pwf, j-主井筒第j微元段的井筒压力,MPa;
ft, ij-第i分支第j微元的壁面摩擦系数,计算方法参见文献[4];
Di-第i分支的井筒内径,m;
qw, ij-第i分支的第j微元段的平均截面流量,m3/s;
qws, ij-第i分支的第j微元段的径向入流量,m3/(m·s);
lij-第i分支第j微元段长度,m;
qws, im-第i分支的第m微元段的径向入流量,m3/(m·s);
lim-第i分支的第m微元段的长度,m。
4 耦合流动模型根据分支水平井各分支微元段的油藏流动在井壁处的压力与井筒流动在井壁处的压力相等这一关系,结合油藏渗流方程式(1)、(2)和井筒流动压降方程式(3)、(8)可得油藏渗流和井筒流动的耦合模型为
| $ \begin{array}{l} {A_1}Q = {C_1}\\ {A_2}P = {C_2}\\ {A_3}{P_0} = {C_3} \end{array} $ | (14) |
分支不对称时,储层微元分布有1个、2个分支微元段是间隔交替出现的,其分支长度,分支的排列间距,切片的疏密均会改变系数A1的情况。因此对于系数A1的构建,需根据微元细分的实际情况制定,以图 1为例,假设各分支长度相等,每分支分为6个微元段时,每分支在主井筒上间隔4个储层微元,每分支(i分支)后面两微元段与下一分支(i+1)的前两微元段出现在同一微元切片上,根据上述规律构建的方程系数矩阵分别如下,可以看出系数矩阵A1、A2和A3均为对角稀疏矩阵,求解该类问题可节约计算时间。
| $ {A_1} = {\left[\begin{array}{l} {a_{11}}\;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\;0\\ 0\;\;{a_{12}}\;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\;0\\ 0\;\; \cdots \;\;{a_{13}}\;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\;0\\ 0\;\; \cdots \;\; \cdots \;\;{a_{14}}\;\; \cdots \; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\;0\\ 0\;\; \cdots \;\; \cdots \;\; \cdots \;\;{a_{15}}\;\;0\;\;{b_{21}}\;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\;0\\ 0\;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\;{a_{16}}\;\;0\;\;{b_{22}}\;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\;0\\ 0\;\; \cdots \;\; \cdots \;\; \cdots \;\;{b_{15}}\;\;0\;\;{a_{21}}\;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\;0\\ 0\;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\;{b_{16}}\;\;0\;\;{a_{22}}\;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\;0\\ 0\;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\;{a_{23}}\;\; \cdots \;\; \cdots \;\; \cdots \;\;0\\ \vdots \\ 0\;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\;{a_{45}}\;\;0\\ 0\;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\;0\;\;{a_{46}} \end{array} \right]_{24}} $ |
| $ {A_2} = {\left[\begin{array}{l} 1\;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\;0\\ -1\;\;1\;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\;0\\ 0\;\;-1\;\;1\;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\;0\\ 0\;\; \cdots \;\;-1\;\;1\;\; \cdots \; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\;0\\ 0\;\; \cdots \;\; \cdots \;\; - 1\;\;1\;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\;0\\ 0\;\; \cdots \;\; \cdots \;\; \cdots \;\; - 1\;\;1\;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\;0\\ 0\;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; - 1\;\;1\;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\;0\\ 0\;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; - 1\;\;1\;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\;0\\ 0\;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; - 1\;\;1\;\; \cdots \;\; \cdots \;\; \cdots \;\;0\\ \vdots \\ 0\;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; \cdots \;\; - 1\;\;1 \end{array} \right]_{24}} $ |
| $ {A_3} = {\left[\begin{array}{l} 1\;\; \cdots \;\;{\kern 1pt} \cdots \;\; \cdots \;\;0\\ -1{\kern 1pt} \;\;1\;\; \cdots \;\; \cdots \;\;0\\ \vdots \\ 0\;\; \cdots \;\; \cdots \;\;-1\;\;1 \end{array} \right]_{18}} $ |
| $ {C_1} = {\left[\begin{array}{l} {p_e}-{p_{11}}\\ \cdots \\ {p_e}-{p_{16}}\\ \cdots \\ {p_e}-{p_{21}}\\ \cdots \\ {p_e} - {p_{26}}\\ \cdots \\ {p_e} - {p_{41}}\\ \cdots \\ {p_e} - {p_{46}} \end{array} \right]_{24}} - {\rho _{\rm{o}}}{\rm{g}}{z_{\rm{W}}} $ |
| $ {C_2} = {\left[\begin{array}{l} \Delta {p_{{\rm{ac}}{{\rm{c}}_{11}}}} + \Delta {p_{{\rm{wall}}, 11}} + \Delta {p_{{\rm{mi}}{{\rm{x}}_{11}}}} + \Delta {p_{{\rm{w}}{{\rm{f}}_{10}}}}\\ \cdots \\ \Delta {p_{{\rm{ac}}{{\rm{c}}_{16}}}} + \Delta {p_{{\rm{wall}}, 16}} + \Delta {p_{{\rm{mi}}{{\rm{x}}_{16}}}}\\ \cdots \\ \Delta {p_{{\rm{ac}}{{\rm{c}}_{21}}}} + \Delta {p_{{\rm{wall}}, 21}} + \Delta {p_{{\rm{mi}}{{\rm{x}}_{21}}}} + \Delta {p_{{\rm{w}}{{\rm{f}}_{20}}}}\\ \cdots \\ \Delta {p_{{\rm{ac}}{{\rm{c}}_{26}}}} + \Delta {p_{{\rm{wall}}, 26}} + \Delta {p_{{\rm{mi}}{{\rm{x}}_{26}}}}\\ \cdots \\ \Delta {p_{{\rm{ac}}{{\rm{c}}_{41}}}} + \Delta {p_{{\rm{wall}}, 41}} + \Delta {p_{{\rm{mi}}{{\rm{x}}_{41}}}} + \Delta {p_{{\rm{w}}{{\rm{f}}_{40}}}}\\ \cdots \\ \Delta {p_{{\rm{ac}}{{\rm{c}}_{46}}}} + \Delta {p_{{\rm{wall}}, 46}} + \Delta {p_{{\rm{mi}}{{\rm{x}}_{46}}}} \end{array} \right]_{24}} $ |
| $ {C_3} = {\left[\begin{array}{l} \Delta {p_{{\rm{wall}}, 1}} + \Delta {p_{{\rm{con, 1}}}} + \Delta {p_{{\rm{wf, 0}}}}\\ \vdots \\ \Delta {p_{{\rm{wall}}, 2}} + \Delta {p_{{\rm{con, 2}}}}\\ \vdots \\ \Delta {p_{{\rm{wall}}, 18}} + \Delta {p_{{\rm{con, 18}}}} \end{array} \right]_{18}} $ |
其中
| $ {a_{ij}} = \frac{{{B_{\rm{o}}}{\mu _{\rm{o}}}}}{{{\rm{2\pi }}K}}\left( {\ln \frac{{4h}}{{{\rm{\pi }}{r_{\rm{w}}}}} + \ln \tan \;\frac{{{\rm{\pi }}{z_{\rm{w}}}}}{{2h}}} \right) $ |
| $ {b_{ij}} = \frac{{{B_{\rm{o}}}{\mu _{\rm{o}}}}}{{{\rm{2\pi }}K}}\ln \frac{{\left( {{\rm{ch}}\frac{{{\rm{\pi }}{d_{ij}}}}{h} + \cos \frac{{{\rm{\pi }}{z_{\rm{w}}}}}{h}} \right)\left( {{\rm{ch}}\frac{{{\rm{\pi }}{d_{ij}}}}{h} - \cos \frac{{{\rm{\pi }}{r_{\rm{w}}}}}{{2h}}} \right)}}{{\left( {{\rm{ch}}\frac{{{\rm{\pi }}{d_{ij}}}}{h} + \cos \frac{{{\rm{\pi }}{r_{\rm{w}}}}}{{2h}}} \right)\left( {{\rm{ch}}\frac{{{\rm{\pi }}{d_{ij}}}}{h} - \cos \frac{{{\rm{\pi }}{z_{\rm{w}}}}}{h}} \right)}} $ |
分支对称是一种更为特殊的鱼骨分支水平井,如图 4所示。对于此类分支井,也可运用本文方法构建方程的系数,且构建的方程组求解更加简便。对于任意微元切片,如图 4所示,各储层微元包含有2个(若分支间距更大,则也有包含0个分支微元的情况)分支微元段,且由于是对称分布的,各对称分支的压降、流量均相等,因此微元切片上2分支微元井段的流量是相等的,因此二者之间干扰下的各分支井筒微元段井底势差与流量之间的关系式,采用等产量2分支井的干扰模型来确定方程中微元势降与流量的关系,表达式如式(15)。
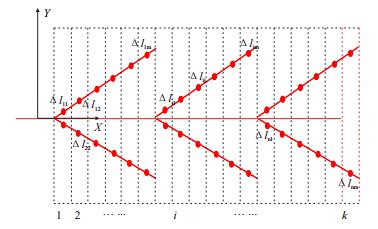 |
| 图4 分支对称的鱼骨分支水平井微元段划分示意图 Fig. 4 Micro-unit division in the symmetrical herringbone branched horizontal well |
| $ {\mathit{\Phi} _{\rm{e}}} - {\mathit{\Phi} _{{\rm{wf}}, ij}} = \frac{{{B_{\rm{o}}}{\mu _{\rm{o}}}}}{{{\rm{2\pi }}K}}\left( {\ln \frac{{4h}}{{{\rm{\pi }}{r_{\rm{w}}}}} + \ln \tan \;\frac{{{\rm{\pi }}{z_{\rm{w}}}}}{{2h}} + {F_{ij}}} \right){q_{{\rm{ws}}, ij}} $ | (15) |
式中:
| $ {F_{ij}} = \ln \frac{{\left( {{\rm{ch}}\frac{{{\rm{\pi }}{d_{ij}}}}{h} + \cos \frac{{{\rm{\pi }}{z_{\rm{w}}}}}{h}} \right)\left( {{\rm{ch}}\frac{{{\rm{\pi }}{d_{ij}}}}{h} - \cos \frac{{{\rm{\pi }}{r_{\rm{w}}}}}{{2h}}} \right)}}{{\left( {{\rm{ch}}\frac{{{\rm{\pi }}{d_{ij}}}}{h} + \cos \frac{{{\rm{\pi }}{r_{\rm{w}}}}}{{2h}}} \right)\left( {{\rm{ch}}\frac{{{\rm{\pi }}{d_{ij}}}}{h} - \cos \frac{{{\rm{\pi }}{z_{\rm{w}}}}}{h}} \right)}} $ |
| $ {d_{ij}} = \sqrt {{{\left( {{x_{ij}} - {x_{\left( {i + 1} \right)}}} \right)}^2} + {{\left( {{y_{ij}} - {y_{\left( {i + 1} \right)j}}} \right)}^2}} $ |
且dij=d(i + 1)j,此处
上述对称的鱼骨分支水平井相比不对称鱼骨井而言,耦合方程的系数矩阵得到进一步简化,组成的非线性方程组仍可运用高斯迭代法求解,计算会更省时间。
5 实例计算分析底水油藏、流体物性、分支水平井结构等基本参数如表 1所示。
| 表1 地质模型参数 Table 1 Parameters used in the simulations |
当井筒半径较小时井筒压降明显,当井筒半径较大时,井筒压降不明显,对比了1 mPa势差、不同井径造成的不同压降水平下本文简化模型与精确模型的产能计算结果。
对比分析简化模型和精确模型结果发现(图 5和图 6),简化模型采用了文献[15]的近似渗流公式,公式在进行镜像反映、势的叠加级数求和计算过程中,采取了一系列的近似与化简,会产生计算结果偏小的误差。如图 5所示,对简化模型进行+10.0%修正后与精确模型结果基本一致,同样对图 6中简化模型进行+12.2%修正,也基本与精确模型一致。图 5和图 6代表不同井径的误差分析情况,两图的平均误差为-11%。
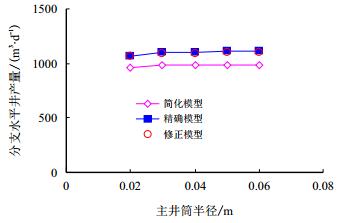 |
| 图5 分支井筒半径为0.02 m时不同主井筒半径对产量影响 Fig. 5 Productivity influenced by different radius of main well bores when the multilateral wellbore radius is 0.02 m |
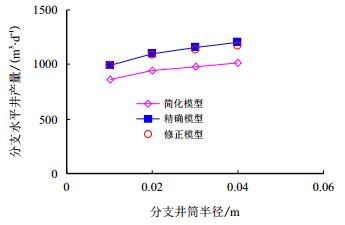 |
| 图6 主井筒半径为0.04 m时不同分支井筒半径对 Fig. 6 Productivity influenced by different radius of multilateral well bores when the main wellbore radius is 0.04 m |
此外,从图 5可以看出,由于主井筒不参与生产,仅仅参与导流,因此主井筒半径超过0.03 m后,已足够满足1 MPa势差生产时,对主井筒导流能力的要求,井筒压降对产量的影响较小。从图 6可以看出,由于生产井段为分支井段,分支井筒不仅参与渗流而且还参与导流,因此分支井筒半径对产能的影响会始终存在,当分支井筒半径小于0.02 m时,分支跟端导流能力受到限制,井筒压降对产能的影响较为敏感,超过0.02 m后,导流能力足够,井筒压降影响较小,此时分支井筒半径主要影响储层渗流能力。
5.1.2 井筒位置对计算误差的影响选择井筒压降较为明显(主分支井筒半径rw=0.02 m)和压降基本可以忽略(rw=0.04 m)的情形,分别研究了井筒垂向偏心位置对计算误差的影响。
图 7和图 8为油井不同垂向位置和井筒半径下,利用本文简化模型结果同完全精确模型的对比,可以看出两公式随井筒位置(避水高度)zw的增加,单位压差下的产量均逐步减小,二者变化趋势基本一致,但简化模型计算结果均小于精确模型,其原因同前所述。计算分析表明,如图 7所示,当井筒半径较小、压降较为明显时,简化模型平均误差约为-9.8%;而当井筒半径较大(如图 8所示)、压降不明显时,简化模型平均误差约为-11.4%。按各自比例进行修正后,可以看出修正模型与精确模型结果基本接近。上述图 7和图 8分别代表了井筒压降影响明显和不明显的情况,两种情况的平均误差为-10.5%。
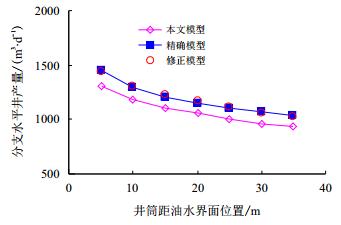 |
| 图7 rw=0.02 m时偏心位置对计算误差影响 Fig. 7 Influence of eccentric position on calculation deviation when rw=0.02 m |
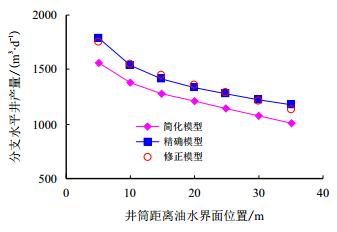 |
| 图8 rw=0.04 m时偏心位置对计算误差影响 Fig. 8 Influence of eccentric position on calculation deviation when rw=0.04 m |
综合图 5至图 8的误差分析可知,由于本文采用了文献[15]提供的势叠加、级数求和近似处理,本例简化模型与精确模型的平均偏差在-11%左右。
5.2 计算速度对比对于本例计算,迭代求解过程中方程的矩阵系数为稀疏矩阵,迭代求解速度远远快于全系数矩阵,分别进行不同井径情况下共计12批次计算,CPU运算时间统计表明,本例计算一次CPU平均用时2.8 s,完全解析模型CPU平均运算时间为8.7 s,本例计算时间约为精确模型的1/3,对于微元细分段数更多的情况,本例可以节约的时间优势会更明显。
5.3 分支井入流剖面分析选用表 1中的基本参数,计算分析了不同主、分支井筒半径对分支入流剖面的影响。
5.3.1 不同主井筒半径的影响从图 9可以看出,当主井筒半径较小时(rw=0.02 m),其导流能力受到明显限制,从主井筒跟端位置处的分支1到距离主井筒跟端最远的分支4,井筒压降依次增加,分支井各微元井底流压依次增加,因此产量依次减小。随主井筒半径增加,分支井的这种差别越来越小,当主井筒半径rw=0.06 m,其导流能力充足,各分支井流量几乎相当。
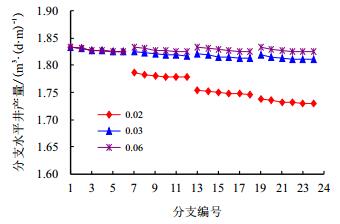 |
| 图9 分支井筒半径为0.02 m时不同主井筒半径对分支井入流量的影响 Fig. 9 Influence of different main wellbore radius on influx of multilateral well when the multilateral wellbore radius is 0.02 m |
从图 10可以看出,当分支井筒半径较小时(rw=0.01 m),分支自身导流能力受到明显限制,即同一分支上从趾端到跟端各微元流量降幅明显。当分支半径超过0.02 m后,分支导流能力基本对分支各微元产量影响不大。图 10也同时说明分支井筒半径越大,分支流量越高。
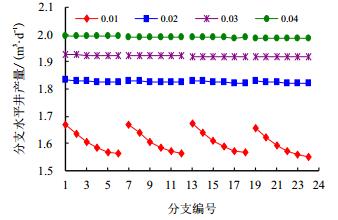 |
| 图10 主井筒半径为0.04 m不同的分支井筒半径对分支井入流量的影响 Fig. 10 Influence of different multilateral wellbore radius on influx of multilateral well when the main wellbore radius is 0.04 m |
由前面分析可以知道,井筒半径在一定范围内对耦合简化模型的流量和压降的影响明显,不同的井径对井筒的压降影响如图 11所示。
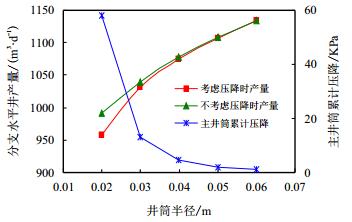 |
| 图11 井筒内径对井筒压降及产量影响 Fig. 11 Influence of wellbore radius on wellbore pressure drop and production |
不同井径计算的主井筒累计压降、分支水平井总产量、及不考虑井筒压降时的分支水平井总产量如图 11所示。井筒越细小,井筒内流体越难流动,造成主井筒累计压降越大,相应的井筒压降造成的产量差别也越大。
对于其他类型参数对井筒流量和压降的影响,运用本文的耦合公式均可做参数敏感性计算,限于篇幅本文未一一阐述。
6 结论(1)新的微元处理方法和手段着眼于储层细分,相比井段细分而言,该简化耦合模型能够大大简化耦合方程的系数矩阵,利于方程组的迭代求解,节约计算成本,尤其是对于结构规则、各分支结构参数相同(等长度、等间距、等夹角)、两侧分支对称的鱼骨分支水平井,其节约的计算时间更为明显。
(2)井筒偏心位置、井筒内径大小等参数对分支井产能和井筒压降的影响,精确与简化模型的规律变化趋势基本一致。简化模型节约了计算成本,也牺牲了一定的计算精度,简化模型预测的产能相对于精确耦合模型误差约为-11%,按此比例修正后可用于底水油藏鱼骨分支水平井产能的快速估算。
(3)水平井、分支水平井井筒流动与油藏渗流耦合模型,其流量剖面的预测精度受井筒压降模型精度影响,不论数理上多么精确的模型,在井筒压降计算模型获得足够精度之前,均不可避免存在一定程度的误差,矿场实际更青睐忽略压降影响的计算方法或通过简化、修正公式进行近似求解。
| [1] | Basquet R, Alabert F G, Caltagirone J P, et al. A semianalytical approach for productivity evaluation of wells with complex geometry in multilayered reservoirs[C]. SPE 49232, 1998. https://www.onepetro.org/conference-paper/SPE-49232-MS |
| [2] | Wolfsteiner C, Durlofsky L J, Aziz K. Approximate model for productivity of nonconventional wells in heterogeneous reservoirs[C]. SPE 62812, 2000. https://www.onepetro.org/journal-paper/SPE-62812-PA |
| [3] | Ouyang L B, Aziz K. A general single-phase wellbore/reservoir coupling model for multilateral wells[C]. SPE 72467, 2001. https://www.onepetro.org/journal-paper/SPE-72467-PA |
| [4] | Ouyang L B, Arbabi S, Aziz K. General wellbore flow model for horizontal, vertical, and slanted well completion[C]. SPE 36608, 1998. http://cat.inist.fr/?aModele=afficheN&cpsidt=6271403 |
| [5] | Tabatabaei M, Ghalambor A. A new method to predict performance of horizontal and multilateral wells[C]. SPE 13122, 2009. https://www.onepetro.org/conference-paper/IPTC-13122-MS |
| [6] |
刘想平, 张兆顺, 崔桂香, 等. 鱼骨型多分支井向井流动态关系[J].
石油学报, 2000, 21 (6) : 57 –60.
Liu Xiangping, Zhang Zhaoshun, Cui Guixiang, et al. Inflow performance relationship of a herringbone multilateral well[J]. Acta Petrolei Sinica, 2000, 21 (6) : 57 –60. |
| [7] |
黄世军, 程林松, 李秀生, 等. 多分支水平井压力系统分析模型[J].
石油学报, 2003, 24 (6) : 81 –86.
Hung Shijun, Cheng Linsong, Li Xiusheng, et al. Pressure system analysis model for multi-lateral horizontal well[J]. Acta Petrolei Sinica, 2003, 24 (6) : 81 –86. |
| [8] | 黄世军, 程林松. 复杂结构井变质量管流与地层渗流祸合模型[J]. 中国科学技术大学学报, 2004, 34 (增刊) : 19 –25. |
| [9] |
陈卫东, HillA D. 多分支井产能预测方法[J].
中国海上油气, 2006, 18 (6) : 394 –398.
Chen Weidong, Hill A D. Development of multilateral well deliverability model[J]. China Offshore Oil and Gas, 2006, 18 (6) : 394 –398. |
| [10] |
杨小松, 刘传喜, 严谨, 等. 鱼骨型多分支水平气井产能规律研究[J].
石油学报, 2008, 29 (5) : 727 –733.
Yang Xiaosong, Liu Chuanxi, Yan Jin, et al. Research on productivity law of herringbone multilateral gas well[J]. Acta Petrolei Sinica, 2008, 29 (5) : 727 –733. |
| [11] | 段永刚, 陈伟, 李冬梅, 等.底水油藏多分支井水脊突破规律研究[C]//重庆:第十一届全国渗流力学学术大会论文集, 2011. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-AGLU201104001017.htm |
| [12] |
段永刚, 陈伟, 黄诚, 等. 井筒与油藏耦合条件下的水平井非稳态产能预测(1)-数学模型[J].
西南石油学院学报, 2004, 26 (1) : 23 –25.
Duan Yonggang, Chen Wei, Huang Cheng, et al. Transient performance prediction of horizontal well with coupled in wellbore and reservoir part 1:Mathematic model[J]. Journal of Southwest Petroleum Institute, 2004, 26 (1) : 23 –25. |
| [13] |
安永生. 油藏各向异性对鱼骨状分支井产能影响分析[J].
西南石油大学学报:自然科学版, 2011, 33 (3) : 145 –148.
An Yongsheng. Analysis of influences of the reservoir anisotropy on productivity of herringbone multi-lateral well[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2011, 33 (3) : 145 –148. |
| [14] |
张殿锋. 鱼骨状分支水平井井筒流动特征及影响因素分析[J].
断块油气田, 2012, 19 (6) : 796 –799.
Zhang Dianfeng. Wellbore flow characteristics and its influencing factors of fish-bone branch horizontal wells[J]. Fault-block Oil & Gas Field, 2012, 19 (6) : 796 –799. |
| [15] |
范子菲. 底水驱动油藏水平井产能公式研究[J].
石油勘探与开发, 1993, 20 (1) : 71 –75.
Fan Zifei. Study for horizontal well's productivity formula in bottom-water drive reservoir[J]. Petroleum Exploration and Development, 1993, 20 (1) : 71 –75. |
| [16] |
时宇, 杨正明, 张训华. 气顶底水油藏水平井井间干扰研究[J].
大庆石油地质与开发, 2008, 27 (5) : 62 –66.
Shi Yu, Yang Zhengming, Zhang Xunhua. Interwell interference study on horizontalwell in gas cap oil[J]. Petroleum Geology & Oilfield Development in Daqing, 2008, 27 (5) : 62 –66. |
 2015, Vol. 37
2015, Vol. 37


