2. 中国科学院力学研究所博士后流动站, 北京 海淀 100190
2. Postdoctoral General of Institute of Mechanics, Chinese Academy of Sciences, Haidian, Beijing 100190, China
天然气水合物是近几十年来在海洋和陆地冻土带发现的新型洁净能源。据估算,全球水合物中蕴藏的天然气总量约(1.8~2.1)×1016m3,主要分布在水深大于300 m的海洋及陆地永久冻土带沉积物中,其储量相当于全球已探明传统化石燃料(煤、石油和天然气)总碳量的两倍[1]。水合物的赋存稳定性对温度和压力条件十分敏感,极易发生分解。常温常压下,1 m3的水合物分解将产生164.6 m3的甲烷和0.87 m3的自由水[2],若水深为1 000 m,将导致体积膨胀接近1倍,如此规模的体积膨胀将致使地层超孔隙压力急剧增加,有效应力降低,促使含水合物地层发生大范围变形或失稳破坏,例如海底滑坡[3-5]、沉积物滑塌[6]、海底麻坑和泥火山的形成[7-9]、软沉积物变形[10]及海底小山丘的形成[11]等。此外,作为一种温室效应较为严重的气体,海底天然气水合物的分解对全球气候的变化和海洋生态环境都将产生重大影响[12]。因此,准确预测水合物分解产生的超孔隙压力显得尤为必要。
Grozic J L H等[13]建立了预测含气土和含水合物土体响应的力学模型,通过引入热力学概念获得了水合物分解产生的超孔隙压力。但模型中存在取值难定的非常规土体参数,因此,该模型应用范围有限,且文献中并未列出超孔隙压力模型的推导过程。
Fleming P B等[14]基于现场实测数据,采用经验方法预测了美国北卡罗来纳州大洋钻探计划997号站布莱克海峡水合物储层分解产生的超孔隙压力。显然,经验预测法不能动态反馈水合物分解及沉积物压缩与超孔隙压力之间的关系。
Sultan N等[15]定量研究了有限孔隙空间内水合物分解产生的超孔隙压力。但该研究仅考虑了有限空间内水合物分解产生的最大超孔隙压力,且采用CO2水合物试验数据近似代替甲烷水合物,因此相关结论有待进一步验证。
Xu W和Germanovich L N[16]定量研究了不同渗透性能的海洋沉积物中水合物分解产生的超孔隙压力,建立了理论模型并初步考察了不同参数的影响大小,探讨了水合物分解的不同触发机制,建议了一定的规避措施。但该模型形式为微分形式,不仅存在无法确定的土体参数,还引入了无法定量的水合物分解时间,模型适用性有限。
采用热力学基本思想,建立了水合物分解导致沉积物体积膨胀的计算模型。在此体积膨胀模型基础之上,利用土体压缩和回弹特性建立了沉积物体积变化和有效应力的关系,获得了水合物分解引起的超孔隙压力理论解析模型。最后,本文针对特定的海底滑坡工程实例对超孔隙压力模型进行验证,并展开参数考察,分析各参数的影响效应。本文研究对认识水合物分解产生的超孔隙压力演变机理,保证水合物储层的稳定性,规避水合物分解带来工程风险具有重要的理论价值和现实意义。
1 水合物分解导致沉积物体积膨胀天然气水合物分解将产生大量的甲烷气体并致使孔隙体积膨胀,假设水合物分解前沉积物为饱和状态,即孔隙体积全部由固体水合物和自由水填充,且热传递和外界压力改变较孔隙压力变化更为急剧。在常温常压条件下,建立水合物沉积物初始状态和完全分解后最终状态下的相态模型,如图 1所示。
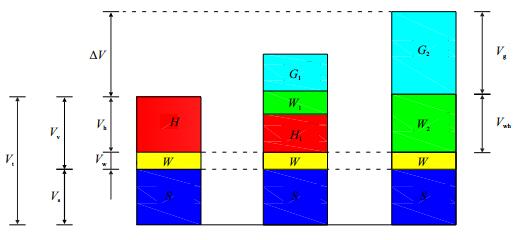 |
| 图1 水合物分解的相态模型 Fig. 1 Phase behavior model for hydrate dissociation |
图中:S-固体土颗粒的体积分数,无因次;W-自由水的体积分数,无因次;H-水合物的体积分数,无因次;W1-水合物分解产生的水的中间量;W2-水合物全部分解后产生的水的体积分数,无因次;G1-水合物分解产生的气体的中间量;G2-水合物全部分解后产生的气体的体积分数,无因次;H1-水合物分解中间阶段剩余水合物的体积分数,无因次;Vh-固体水合物的体积,m3;Vw-自由水的体积,m3;Vs-固体土颗粒的体积,m3;Vv-孔隙的体积,m3;Vt-水合物沉积物的总体积,m3;Vg-水合物全部分解后产生的气体的体积,m3;Vwh-水合物全部分解后产生的水的体积,m3;ΔV-水合物分解引起的总体积变化,m3。
设水合物未分解的初始状态总体积为1 m3,则孔隙率为
| $ n = \frac{{{V_{\rm{V}}}}}{{{V_{\rm{t}}}}} = {V_{\rm{v}}} $ | (1) |
式中:
n-孔隙率,无因次。
在初始状态时,根据图 1所示的体积关系有
| $ {V_{\rm{v}}} = {V_{\rm{h}}} + {V_{\rm{w}}} $ | (2) |
由此,自由水的饱和度为
| $ {S_{\rm{r}}} = \frac{{{V_{\rm{w}}}}}{{{V_{\rm{v}}}}} $ | (3) |
式中:
Sr-自由水的饱和度,无因次。
将式(1)和式(2)代入式(3),消去自由水的体积Vw,得
| $ {S_{\rm{r}}} = \frac{{n - {V_{\rm{h}}}}}{n} $ | (4) |
将式(4)变形,可得
| $ {V_{\rm{h}}} = n\left( {1 - {S_{\rm{r}}}} \right) $ | (5) |
在常温常压条件下,1 m3的水合物分解将产生164.6 m3的甲烷和0.87 m3的自由水。在水合物完全分解之后,水合物的体积会转变为气体的体积和水的体积。因此,水合物分解引起的体积变化可表示为
| $ \Delta V = {V_{\rm{g}}} + {V_{{\rm{wh}}}} - \Delta {V_{\rm{g}}} - {V_{\rm{h}}} $ | (6) |
在水合物分解过程中认为土颗粒和水不可压缩,因此自由水和土颗粒的体积保持不变。将ΔVg表示为
| $ \Delta {V_{\rm{g}}} = {V_{{\rm{g}}\left( {i + 1} \right)}} - {V_{{\rm{g}}i}} $ | (7) |
式中:
Vg(i+1)水合物分解引起某阶段压力增加下的自由气体体积,m3;
Vgi某分解阶段前压力未增加下的自由气体体积,m3;
下标:i水合物分解的增量步。
根据波义耳定律
| $ {p_{i + 1}}{V_{{\rm{g}}\left( {i + 1} \right)}} = {p_i}{V_{{\rm{g}}i}} $ | (8) |
式中:
pi+1水合物分解引起某阶段压力增加下的压强,Pa;
pi某分解阶段前压力未增加下的压强,Pa。
由式(8)可得
| $ \Delta {V_{\rm{g}}} = {V_{{\rm{g}}i}}\left( {\frac{{{p_i}}}{{{p_{i + 1}}}} - 1} \right) $ | (9) |
每一阶段水合物分解气体体积都会增加,因为每一次循环计算,水合物分解将释放更多的气体。将式(5)和式(9)代入式(6)可得水合物分解引起的总体积变化
| $ \Delta V = {V_{\rm{g}}} - 0.13n\left( {1 - {S_{\rm{r}}}} \right) - {V_{{\rm{g}}i}}\left( {\frac{{{p_i}}}{{{p_{i + 1}}}} - 1} \right) $ | (10) |
如果水合物分解过程发生在常温常压条件下,则可直接用式(10)计算体积变化。然而,实际情况下的温压条件与常温常压条件并不一致,此时假设气体的摩尔体积不变,可用通用气体定律来计算原位温压条件下的气体体积
| $ \left\{ {\begin{array}{*{20}{l}} {{m_{{\rm{STP}}}} = {m_{{\rm{ep}}}}}\\ {\frac{{{\rm{R}}{T_{{\rm{STP}}}}}}{{{p_{{\rm{STP}}}}{V_{{\rm{gSTP}}}}}} = \frac{{{\rm{R}}{T_{{\rm{eq}}}}}}{{{p_{{\rm{eq}}}}{V_{\rm{g}}}}}} \end{array}{\rm{ }}} \right. $ | (11) |
式中:
mSTP-常温常压条件下的气体摩尔体积,L/mol;
meq-实际温压情况下的气体摩尔体积,L/mol;
R气体常数,J/(mol·K);
TSTP-常温,K;
pSTP-常压,Pa;
VgSTP-常温常压下的气体体积,m3;
Teq-天然水合物稳定的临界平衡温度,K;
peq-天然水合物稳定的临界平衡压力,Pa。
在纯水条件下,天然气水合物稳定的临界平衡温压关系可由经验公式表示为ln(peq×1000)=38.98-8533.8/Teq。在海水条件下(设海水盐度为3.5%),天然气水合物稳定的临界温度将降低约1.5℃,即盐度含量对水合物的形成具有一定的抑制作用。
常温常压条件下有TSTP-=298.15 K,pSTP-=1.013×105 Pa,VgSTP=164.6 Vh,由此可得
| $ \frac{{298.15}}{{1.013 \times {{10}^5} \times 164.6{V_{\rm{h}}}}} = \frac{{{T_{{\rm{eq}}}}}}{{{p_{{\rm{eq}}}}{V_{\rm{g}}}}} $ | (12) |
因此原位温压条件下的气体体积可表示为
| $ {V_{\rm{g}}} = \frac{{1.013 \times {{10}^5} \times 164.6 \times {V_{\rm{h}}} \times {T_{{\rm{eq}}}}}}{{298.15 \times {p_{{\rm{eq}}}}}} $ | (13) |
将式(13)代入式(10),可得水合物分解导致沉积物的体积变化为
| $ \begin{array}{l} \Delta V = \frac{{1.013 \times {{10}^5} \times 164.6 \times n\left( {1 - {S_{\rm{r}}}} \right) \times {T_{{\rm{eq}}}}}}{{298.15 \times {p_{{\rm{eq}}}}}} - \\ 0.13n\left( {1 - {S_{\rm{r}}}} \right) - {V_{{\rm{g}}i}}\left( {\frac{{{p_i}}}{{{p_{i + 1}}}} - 1} \right) \end{array} $ | (14) |
为了确定水合物沉积物对分解导致的体积变化的响应,需获得体积变化与沉积物有效应力的关系。因水合物分解将导致沉积物孔隙压力增大,同时有效应力减少,此过程与土体在压缩固结过程之后的卸载回弹过程一致,土体有膨胀趋势。因此考虑利用土体压缩和回弹的相关指标用于建立体积变化和有效应力的关系。引入衡量土体在体积应力作用下产生体积改变能力的指标——体积变形系数
| $ {m_{\rm{v}}} = \frac{{\Delta \varepsilon }}{{\Delta \sigma '}} $ | (15) |
式中:
mv-体积变形系数,kPa-1;
Δε-水合物分解产生的应变变化,无因次;
Δσ′-水合物分解导致的有效应力变化,kPa。
引入压缩模量
| $ {E_{\rm{s}}} = \frac{1}{{{m_{\rm{v}}}}} = \frac{{\Delta \sigma '}}{{\Delta V/{V_{\rm{t}}}}}{\rm{ }} $ | (16) |
式中:
Es压缩模量,kPa。
将式(16)变形,可得体积变化和有效应力的关系
| $ \frac{{\Delta V}}{{{V_{\rm{t}}}}} = \frac{{\Delta \sigma '}}{{{E_{\rm{s}}}}} $ | (17) |
因总体积Vt-=1 m3,式(17)可变为
| $ \Delta V = {\rm{ }}\frac{{\Delta \sigma '}}{{{E_{\rm{s}}}}} $ | (18) |
若温度或热传递及压力的变化过程与孔隙压力消散过程相比足够快,则水合物沉积物有效应力的减小,可以通过将式(18)代入式(14)来计算
| $ \begin{array}{l} \frac{{\Delta \sigma '}}{{{E_{\rm{s}}}}} = \frac{{1.013 \times {{10}^5} \times 164.6 \times n\left( {1 - {S_{\rm{r}}}} \right) \times {T_{{\rm{eq}}}}}}{{298.15 \times {p_{{\rm{eq}}}}}} - \\ \;\;\;\;\;\;0.13n\left( {1 - {S_{\rm{r}}}} \right) - {V_{{\rm{gi}}}}\left( {\frac{{{p_i}}}{{{p_{i + 1}}}} - 1} \right)n \end{array} $ | (19) |
式(19)中:左侧项表示由于有效应力变化导致的土体体积变化;右侧第一项表示平衡温度和压力条件下水合物分解释放的气体体积;第二项表示常温常压条件下水合物体积和水合物分解产生的水的体积之差(1.00~0.87 m3);第三项表示由于自由气体压缩引起的体积变化。
考虑方程左侧项,由于土体的压缩模量Es难以确定,因此,需寻求常规参数替代压缩模量。水合物分解导致有效应力的变化进而引起体积变化的过程与土体固结过程相似,体积的变化与沉积物孔隙比的关系可以表示为
| $ \frac{{\Delta V}}{{{V_{\rm{t}}}}} = \frac{{\Delta e}}{{1 + {e_0}}} $ | (20) |
式中:
Δe水合物分解导致的孔隙比变化,无因次;
e0水合物未分解时的初始孔隙比,无因次。
引入压缩系数
| $ {a_{\rm{v}}} = - {\rm{ }}\frac{{\Delta e}}{{\Delta \sigma '}} $ | (21) |
式中:
av压缩系数,kPa-1;
负号孔隙比随有效应力的增加而减小。
将式(20)和式(21)代入式(16),可得
| $ {E_{\rm{s}}} = \frac{{1 + {e_0}}}{{{a_{\rm{v}}}}} $ | (22) |
由前述可知,水合物分解引起有效应力的降低与压缩之后的卸载回弹过程一致,由此,建立压缩系数与膨胀指数的关系,定义膨胀指数
| $ \begin{array}{*{20}{l}} {{C_{\rm{s}}} = \frac{{\Delta e}}{{\Delta \lg \sigma '}} = \frac{{\Delta e}}{{\lg \left( {\sigma ' + \Delta \sigma '} \right) - \lg \sigma '}}}\\ {\;\;\;\; = \frac{{\Delta e}}{{0.434\ln \left( {1 + \frac{{\Delta \sigma '}}{{\sigma '}}} \right)}}} \end{array} $ | (23) |
式中:
Cs膨胀指数,无因次;
σ′有效应力,kPa。
将式(21)和式(23)代入式(22),可得
| $ {E_{\rm{s}}} = \frac{{\left( {1 + {e_0}} \right)\Delta \sigma '}}{{0.434{C_{\rm{s}}}\ln \left( {1 + \frac{{\Delta \sigma '}}{{\sigma '}}} \right)}} $ | (24) |
采用Wroth C P[17]提出的塑性指数、土粒比重和压缩指数的关系,可近似表示为
| $ {C_{\rm{c}}} = \frac{{{I_{\rm{p}}} \times {G_{\rm{s}}}}}{{200}} $ | (25) |
式中:
Cc-压缩指数,无因次;
Ip-塑性指数,无因次;
Gs-土粒比重,无因次。
Wroth指出,当Ip-从15变为100时,Cs/Cc从0.17变为0.34,假设Cs/Cc随Ip的变化为线性关系,则Cs可表示为
| $ {C_{\rm{s}}} = \left( {0.002{I_{\rm{p}}} + 0.14} \right) \times \left( {\frac{{{I_{\rm{p}}} \times {G_{\rm{s}}}}}{{200}}} \right) $ | (26) |
对于仅由于热传递导致的水合物分解,假设在不排水条件下总应力不变,即有效应力的变化与超孔隙压力的变化相等:Δu=-Δσ′。进而,将式(24)带入式(19)消除变量Es,同时联立式(26),得到水合物分解导致的超孔隙压力变化计算表达式
| $ \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} \Delta u = - \Delta \sigma ' = \frac{{\left( {1 + {e_0}} \right)\Delta \sigma '}}{{0.434{C_{\rm{s}}}\ln \left( {1 + \frac{{\Delta \sigma '}}{{\sigma '}}} \right)}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {n\left( {1 - {S_{\rm{r}}}} \right)\left( {0.13 - 164.6\frac{{{T_{{\rm{eq}}}}}}{{298.15}}\frac{{1.013 \times {{10}^5}}}{{{p_{{\rm{eq}}}}}}} \right){\rm{ + }}{V_{{\rm{g}}i}}\left( {\frac{{{p_i}}}{{{p_{i + 1}}}} - 1} \right)} \right] \end{array}\\ {{C_{\rm{s}}} = \left( {0.002{I_{\rm{p}}} + 0.14} \right)\left( {\frac{{{I_{\rm{p}}} \times {G_{\rm{s}}}}}{{200}}} \right)} \end{array}} \right. $ | (27) |
式中:
Δu-水合物分解导致的超孔隙压力变化,kPa。
根据Nixon M F[18]的研究,游离气体体积压缩对沉积物孔隙压力或有效应力的影响不大,通常情况下可以忽略不计,因此,可以将式(27)简化表示为
| $ \left\{ {\begin{array}{*{20}{l}} {\Delta u = - \Delta \sigma ' = \frac{{\Delta \sigma '\left( {1 + {e_0}} \right)}}{{0.434{C_{\rm{s}}}\ln \left( {1 + \frac{{\Delta \sigma '}}{{\sigma '}}} \right)}}n\left( {1 - {S_{\rm{r}}}} \right)\left( {0.13 - 164.6\frac{{{T_{{\rm{eq}}}}}}{{298.15}}\frac{{1.013 \times {{10}^5}}}{{{p_{{\rm{eq}}}}}}} \right)}\\ {{C_{\rm{s}}} = \left( {0.002{I_{\rm{p}}} + 0.14} \right)\left( {\frac{{{I_{\rm{p}}} \times {G_{\rm{s}}}}}{{200}}} \right)} \end{array}} \right. $ | (28) |
通过式(28),采用逐步分解模式计算水合物分解导致的超孔隙压力变化。首先,在水合物分解前,沉积物处于静水压力条件下,初始孔隙压力采用静水条件计算,有效应力不变;其次,进行第一次迭代计算,为促进水合物分解,假设小量水合物分解,即Δσ′→0,则有ln(1+Δσ′/σ′)→Δσ′/σ′,将其代入式(28)即可得第一次迭代计算的超孔隙压力变化值;最后,根据前一步计算得到的超孔隙压力变化值(即有效应力变化值)代入式(28)中逐步迭代计算,即可获获得水合物分解所有步的超孔隙压力大小直至水合物完全分解。
需要说明的是,式(28)仅适用于超孔隙压力迅速聚集且没有发生任何消散的条件,如不排水条件。事实上,孔隙压力可能通过沉积物孔隙或沿裂缝消散,消散的孔隙压力数值取决于地层的相关特性(如渗透性),孔隙压力在低渗透率沉积物中的消散速度比在高渗透率沉积物中低。以上研究假定超孔隙压力瞬时形成,上部有低渗透层,孔隙压力不发生消散,这是一种比较保守的分析。实际上,水合物分解过程中会有部分超孔隙压力发生消散,因此有效应力降低幅度变小,对地层稳定性的影响相对减小。
此外,在实际分析中,增量步大小的选择对孔隙压力的计算至关重要,由于水合物分解具有压力依赖性,每一步分析都会因释放的气体而使压力升高,进而减少在随后分析步中产生的超孔隙压力大小。因此,每一分析步中水合物分解的数量越少或水合物分解速率越低,计算越准确。
3 工程实例分析及参数考察 3.1 自然界滑坡案例研究作为20世纪80年代后期天然气水合物研究的重要成果之一,在挪威西部大陆架发生的与天然气水合物分解有关的大型海底滑坡——Storegga滑坡。该滑坡从挪威西海岸一直延伸至冰岛南部。目前,发生滑坡的原因还不够清楚,诸多潜在因素正在调查,其中,最可能的原因为一次地震,地震使得弱沉积的海洋黏土沉积物发生扰动。然而,无论是从剪切幅度还是滑坡形状来看,存在一种辅助机制使得沉积物发生了大规模的运动,而该辅助机制已经确认为是贯穿整个滑坡区的水合物分解。若该类大型滑坡再次发生,无论是海洋环境,还是滑坡区附近的生物群及工程作业均会受到严重影响,由此引发的海啸和甲烷气体的释放也将不容忽视。工程案例分析中采用的参数取值如表 1所示[15, 19],其中水合物分解层深度和水深均取该滑坡发生海域的平均值。
| 表1 Storegga海底滑坡案例分析参数取值 Table 1 Values of parameters for the analysis of Storegga submarine landslide case |
由于海底沉积物在形成过程中经历了一定程度的早期成岩作用,沉积物中孔隙水之间连通受阻,且天然气水合物的形成也会阻碍孔隙水的连通,阻断了沉积物中孔隙水与底层海水的联系,因此采用静岩压力表征实际的沉积物压力条件更接近客观实际,即
| $ {p_{{\rm{eq}}}} = {\gamma _{\rm{w}}}h + \gamma 'D $ | (29) |
式中:
γw-水的重度,kN/m3;
h水深,m;
γ′沉积物浮重度,kN/m3;
D水合物分解层深度,m。
由表 1可得水合物为分解前,即沉积物稳定条件下的各项力学参数,如表 2所示。
| 表2 沉积物稳定条件下的力学参数 Table 2 Mechanical parameters in the sediment stability condition |
表 2中初始有效应力σ′采用经验公式计算
式中:K0-侧压力系数,无因次,K0=1-sinϕ; ϕ内摩擦角,(°)。
设水合物的分解速率为0.5%,由此可以获得水合物全部分解产生的超孔隙压力变化曲线,如图 2所示。将水合物每分解1%后产生的超孔隙压力值列于表 3。
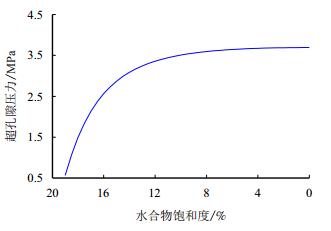 |
| 图2 Storegga海底滑坡水合物分解产生的超孔隙压力 Fig. 2 Excess pore pressure due to hydrate dissociation in Storegga submarine landslide |
| 表3 水合物每分解1%产生的超孔隙压力值 Table 3 Excess pore pressure due to every 1% hydrate dissociation |
由图 2和表 3可知,随水合物不断分解,超孔隙压力不断增加,但增加幅度逐渐降低,在Storegga海底滑坡的工程案例中,在水合物初始饱和度为19%的情况下,若水合物完全分解则产生的最终超孔隙压力为3.692 MPa,该数值逼近地层的初始有效应力3.85 MPa,由此可知,当沉积物中饱和度为19%的水合物全部分解时,产生的超孔隙压力约等于地层的有效应力,致使地层失稳且发生大面积的海底滑坡,该结论与工程案例背景相同且与杨晓云[19]分析结果一致,由此证明超孔隙压力模型的合理性和正确性。
3.2 参数考察孔隙压力模型式(28)表明,影响水合物分解产生的超孔隙压力参数诸多,为分析不同参数的影响效应,对式(28)中的各项参数进行考察。分析式(28)中的各项参数,其中初始孔隙比e0与孔隙率n之间存在关联关系;膨胀指数Cs与塑性指数Ip和土粒比重Gs存在关联关系;自由水饱和度Sr与水合物初始饱和度Sw存在关联关系;水合物平衡温度Teq与平衡压力peq存在关联关系,平衡压力peq又与水深h、浮重度γ'和分解层深度D存在关联关系;初始有效应力σ′与侧压力系数K0、浮重度γ'和分解层深度D存在关联关系,侧压力系数K0又与有效内摩擦角φ存在关联关系。综上所述,与超孔隙压力相关的独立的直接影响参数包括孔隙率n、塑性指数Ip、土粒比重Gs、水合物初始饱和度Sw、水深h、浮重度γ'、分解层深度D和有效内摩擦角φ。由于天然气水合物的地质力学行为研究资料很少,在参数考察中做如下假设:
(1)水合物分解采用理想热交换进行,即分解温度一直在水合物平衡温度以上,在分解中不考虑水合物的二次生成;(2)水合物分解完全且是瞬间完成的;(3)沉积物渗透性能较低,采用不排水条件下的岩土工程特性;(4)不考虑海底坡度的影响,假设沉积物性质一致,水合物分布均匀,分布深度一定,初始饱和度在分布范围内保持不变;(5)水合物的分解速率在整个分解过程中保持不变。
参数考察工况如表 4所示,其中各参数的取值均参照国内外关于水合物沉积物相关参数的典型取值,设定水合物分解速率为0.5%。
| 表4 水合物分解超孔隙压力模型参数考察取值工况 Table 4 Values in parametric analysis in the excess pore pressure model for hydrate dissociation |
参数考察结果如图 3所示,各工况水合物分解产生的最终超孔隙压力值列于表 5。由图可知,对于所有考察工况,随着水合物不断分解,超孔隙压力不断增大,但是增加幅度不断降低,这是由于分解前一步产生的超孔隙压力增大对下一步水合物的分解具有抑制作用。
| 表5 水合物分解产生的最终超孔隙压力值 Table 5 Final values of excess pore pressure due to hydrate dissociation |
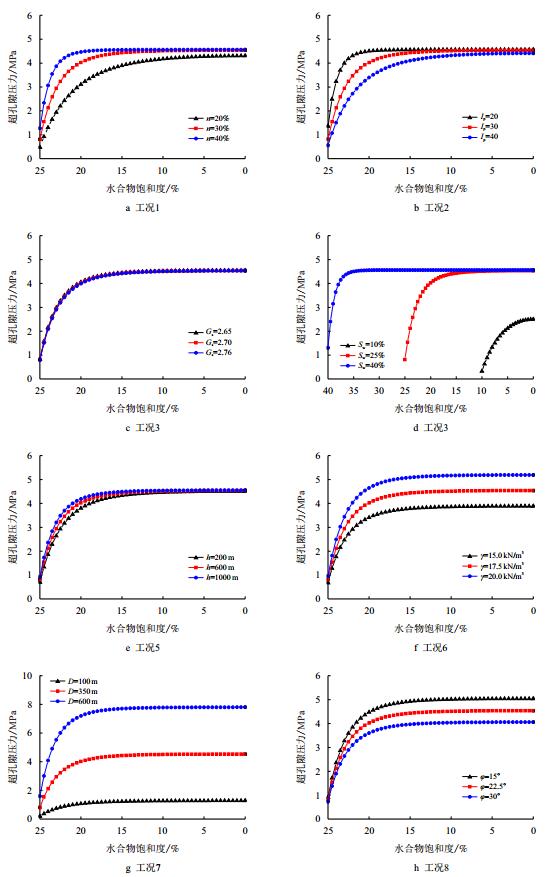 |
| 图3 参数考察分析结果 Fig. 3 Results of parametric analysis |
由图 3a、图 3d~图 3g可知,随着孔隙率n、水合物初始饱和度Sw、水深h、浮重度γ'、分解层深度D的增加,水合物完全分解后产生的超孔隙压力值也增加,由图 3b、图 3c、图 3h可知,随着塑性指数Ip、土粒比重Gs及有效内摩擦角φ的增大,水合物完全分解后产生的超孔隙压力值降低。
从图 3c和图 3e可以发现,土粒比重Gs和水深h对超孔隙压力影响十分微小,由公式(26)可知,一方面由于土粒比重数值相对于分母和塑性指数Ip而言其影响作用较小,另一方面,土粒比重Gs自身的取值范围也有限。而水深h的影响主要体现在初始静水压力的计算中,进而影响水合物的平衡临界压力,而对于特定的海洋环境,水合物平衡的临界温压关系一定,又由于二者在超孔隙压力计算模型中是相除关系,因此其影响作用相应削弱。除土粒比重Gs和水深h影响较小以外,其余各参数的影响均较为明显,其中尤以水合物初始饱和度Sw和分解层深度D的影响最为显著。
分析不同参数的影响效应,由图 3a~图 3c和图 3e可知,孔隙率n、塑性指数Ip、土粒比重Gs和水深h的影响主要体现在水合物分解的初始阶段,在分解初始阶段,超孔隙压力的增长速率有所不同,而在水合物完全分解以后,产生的最终超孔隙压力值相差较小,最大相差仅为5.6%。由图 3d、图 3f~图 3h可知,随着水合物初始饱和度Sw、浮重度γ'、分解层深度D和有效内摩擦角φ的变化,分解产生的超孔隙压力值成倍变化,最大相差有5倍之多。
通过以上参数分析可知,不同参数对超孔隙压力的影响效应不同,针对特定的实际条件,该分析对规避关键影响参数,保证地层稳定性具有重要的指导作用。
4 结论(1)基于水合物分解前后的相态模型,建立了常温常压条件下,天然气水合物分解导致的沉积物体积膨胀公式。进一步通过热力学的通用气体定律将该公式推广至一般条件下,水合物分解导致的体积膨胀模型。
(2)基于体积膨胀模型,利用土体压缩和回弹的相关指标用于建立体积变化和有效应力的关系,进而获得超孔隙压力与体积膨胀之间的关系。利用土体固结等的相关指标和文献经验公式,换算模型中存在的非常规土体参数,最终建立了天然气水合物分解超孔隙压力理论解析模型。
(3)针对超孔隙压力模型,结合典型的海底滑坡工程案例,验证了模型的合理性与正确性,并针对模型中复杂的影响参数展开参数考察,获得了不同参数对超孔隙压力的影响效应。
| [1] | Max M D. Natural gas hydrate in oceanic and permafrost environments[M]. Dordrecht: Kluwer Academic Publishers, 2003 . |
| [2] | Sloan E D. Clathrate hydrate of natural gases[M]. New York: Marcel Dekker, 1998 . |
| [3] | Paull C K, Buelow W J, Ussler W, et al. Increased continental-margin slumping frequency during sea-level lowstands above gas hydrate-bearing sediments[J]. Geology, 1996, 24 (2) : 143 –146. DOI:10.1130/0091-7613(1996)024<0143:ICMSFD>2.3.CO;2 |
| [4] | Rothwell R G, Thomson J, Kähler G. Low-sealevel emplacement of a very large Late Pleistocene 'megaturbidite' in the western Mediterranean Sea[J]. Nature, 1998, 392 (6674) : 377 –380. DOI:10.1038/32871 |
| [5] | Mienert J, Vanneste M, Bünz S, et al. Ocean warming and gas hydrate stability on the mid-norwegian margin at the Storegga Slide[J]. Marine and Petroleum Geology, 2005, 22 (1) : 233 –244. |
| [6] | Dillon W P, Nealon J W, Taylor M H, et al. Seafloor collapse and methane venting associated with gas hydrate on the blake ridge:causes and implications to seafloor stability and methanerelease[M]//Paull C K, Dillon W P. Natural Gas Hydrates:Occurrence, Distribution, and Detection. Washington DC, American:American Geophysical Union, 2001:211-233. http://onlinelibrary.wiley.com/doi/10.1029/GM124p0211/references |
| [7] | Vogt P R, Gardner J, Crane K. The Norwegian-Barents-Svalbard(NBS) continental margin:introducing a natural laboratory of mass wasting, hydrates, and ascent of sediment, pore water, and methane[J]. Geo-Marine Letters, 1999, 19 (1-2) : 2 –21. DOI:10.1007/s003670050088 |
| [8] | Van Rensbergen P, De Batist M, Klerkx J, et al. Sublacustrine mud volcanoes and methane seeps caused by dissociation of gas hydrates in Lake Baikal[J]. Geology, 2002, 30 (7) : 631 –634. DOI:10.1130/0091-7613(2002)030<0631:SMVAMS>2.0.CO;2 |
| [9] | Zühlsdorff L, Spiess V. Three-dimensional seismic characterization of a venting site reveals compelling indications of natural hydraulic fracturing[J]. Geology, 2004, 32 (2) : 101 –104. DOI:10.1130/G19993.1 |
| [10] | Kennett J P, Fackler-Adams B N. Relationship of clathrate instability to sediment deformation in the upper Neogene of California[J]. Geology, 2000, 28 (3) : 215 –218. DOI:10.1130/0091-7613(2000)28<215:ROCITS>2.0.CO;2 |
| [11] | Davies R, Cartwright J, Rana J. Giant hummocks in deepwater marine sediments:Evidence for large-scale differential compaction and density inversion during early burial[J]. Geology, 1999, 27 (10) : 907 –910. DOI:10.1130/0091-7613(1999)027<0907:GHIDWM>2.3.CO;2 |
| [12] | Kennett J P, Cannariato K G, Hendy I L, et al. Methane hydrates in quaternary climate change:The clathrate gun hypothesis[M]. Washington D C: AGU, 2003 . |
| [13] | Grozic J L H, Kvalstad T J. Effect of gas on deepwater marine sediments[C]//Proceedings of The International Conference on Soil Mechanics and Geotechnical Engineering. Aa Balkema Publishers, 2001, 3:2289-2294. |
| [14] | Flemings P B, Liu X, Winters W J. Critical pressure and multiphase flow in Blake Ridge gas hydrates[J]. Geology, 2003, 31 (12) : 1057 –1060. DOI:10.1130/G19863.1 |
| [15] | Sultan N, Cochonat P, Foucher J P, et al. Effect of gas hydrates melting on seafloor slope instability[J]. Marine Geology, 2004, 213 (1) : 379 –401. |
| [16] | Xu W, Germanovich L N. Excess pore pressure resulting from methane hydrate dissociation in marine sediments:A theoretical approach[J]. Journal of Geophysical Research, 2006, 111 (B1) : 1 –12. |
| [17] | Wroth C P. Correlations of some engineering properties of soils[C]//Proceedings of the Second International Conference on the Behaviour of Off-Shore Structures, held at Imperial College, London, England, 1979. Correlations of some engineering properties of soils |
| [18] | Nixon M F. Influence of gas hydrates on submarine slope stability[D]. Albert:University of Calagary, 2005. Influence of gas hydrates on submarine slope stability |
| [19] | 杨晓云.天然气水合物与海底滑坡研究[D].北京:中国石油大学, 2010. http://cdmd.cnki.com.cn/article/cdmd-10425-2010280307.htm |
 2015, Vol. 37
2015, Vol. 37


