西南石油大学学报（自然版）  2015, Vol. 37 Issue (3): 9-16
引用本文
尹洪军, 赵二猛, 付京, 等 .页岩气藏压裂水平井五区复合模型产能分析[J]. 西南石油大学学报（自然版）, 2015, 37(3): 9-16.
Yin Hongjun, Zhao Ermeng, Fu Jing, et al . Production Analysis of Composite Model of Five Regions for Fractured Horizontal Wells in Shale Gas Reservoirs[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2015, 37(3): 9-16.
页岩气藏压裂水平井五区复合模型产能分析    [PDF全文]
尹洪军1,2, 赵二猛1,2, 付京1,2,3, 王磊1,2, 钟会影1,2    
1. 东北石油大学提高采收率教育部重点实验室, 黑龙江 大庆 163318;
2. 东北石油大学非常规油气成藏与开发省部共建国家重点实验室培育基地, 黑龙江 大庆 163318;
3. Geological Science & Engineering, Missouri University of Science and Technology, Rolla, Missouri 65401-6540, USA
收稿日期: 2015-03-04 ; 网络出版时间: 2015-05-20
基金项目: 国家科技重大专项(2011ZX05051);中国石油和化学工业联合会科技项目(2014-01-02)。
作者简介: 尹洪军, 1964年生, 女, 汉族, 黑龙江大庆人, 教授, 博士生导师, 博士, 主要从事油气田开发工程方面的教学和研究工作。E-mail:yinhj7176@126.com;
赵二猛, 1991年生, 男, 汉族, 河南漯河人, 硕士研究生, 主要从事油气渗流理论与应用方面的研究。E-mail:18745953495@163.com;
付京, 1994年生, 女, 汉族, 黑龙江大庆人, 主要从事油气田开发工程方面的研究。E-mail:417430582@qq.com;
王磊, 1990年生, 男, 汉族, 黑龙江大庆人, 硕士研究生, 主要从事油气田开发方面的研究。E-mail:wangleidqpi@163.com。
通信作者: 钟会影, 1981年生, 女, 汉族, 辽宁辽阳人, 讲师, 硕士, 主要从事孔隙级微观渗流理论与应用及油藏数值模拟方面的研究。E-mail:zhhy987@126.com
摘要: 水平井结合水力压裂技术已经成为高效开发页岩气藏的有效手段。为此, 建立并求解了综合考虑页岩气解吸、扩散和渗流特征的页岩气藏压裂水平井五区复合渗流模型, 获得了Laplace空间的产量解析解。运用Stehfest数值反演技术得到了实空间的无因次产量, 绘制并分析了无因次产能递减曲线。研究结果表明:产能递减曲线可划分为6个流动阶段; 窜流系数主要影响解吸扩散及以后的流动阶段; 导流能力主要影响早期裂缝线性流动阶段; 压裂区宽度越大, 产能越大; 压裂区渗透率主要对中后期的产能曲线产生影响, 渗透率越大, 压裂之后形成的缝网与天然微裂缝沟通的越好, 产能越大。研究结果可为页岩气藏分段压裂水平井产能递减分析提供科学依据。
关键词: 页岩气     压裂水平井     五区复合模型     产能分析     吸附解吸    
Production Analysis of Composite Model of Five Regions for Fractured Horizontal Wells in Shale Gas Reservoirs
Yin Hongjun1,2, Zhao Ermeng1,2, Fu Jing1,2,3, Wang Lei1,2, Zhong Huiying1,2    
1. MOE Key Laboratory of Enhanced Oil Recovery, Northeast Petroleum University, Daqing, Heilongjiang 163318, China;
2. Accumulation and Development of Unconventional Oil and Gas, State Key Laboratory Cultivation Base Jointly-constructed by Heilongjiang; Province and the Ministry of Science and Technology, Northeast Petroleum University, Daqing, Heilongjiang 163318, China;
3. Geological Science & Engineering, Missouri University of Science and Technology, Rolla, Missouri 65401-6540, USA
Abstract: Horizontal wells with hydraulic fracturing technology have become an efficient way to produce from shale gas reservoir. Therefore, a composite mathematical model of five regions for fractured horizontal wells in shale gas reservoirs is established in this paper with consideration of desorption, diffusion and percolation characteristics. Then the analytical solution is deduced in Laplace space. Based on the Stehfest numerical inversion algorithms, the analytical solution of dimensionless production in real space is obtained, and dimensional production decline curve is plotted and analyzed. The results show that decline curve can be divided into six different flow regimes according to the characteristics; interporosity flow coefficient mainly influences the shape of desorption and later stages; hydraulic fracture conductivity mainly influences the shape of early linear flow stage, permeability of the stimulated region mainly influences the shape of mid-to late stage. The greater the width of stimulated region is, the higher the production is, and the greater the permeability is, the higher the production is, because the fracture network after being hydraulic fractured is connected well with natural fractures. The results obtained can provide scientific basis for reasonable analysis to production analysis for fractured horizontal wells in shale gas reservoirs.
Key words: shale gas     fractured horizontal wells     composite model of five regions     production analysis     adsorption and desorption    
引言

中国页岩气资源丰富，可采资源量约31.6×1012m3，居世界首位，勘探开发前景广阔[1-2]。页岩气主要以吸附和游离状态存在于页岩之中，其中吸附气含量20%~85%，其渗流机理主要包括页岩基质表面的解析、基质内部的扩散及天然裂缝中的渗流[3-7]。页岩气藏由于孔隙度小，渗透率低，不经压裂基本没有自然产能，而水平井开采结合水力压裂技术已成为目前开发页岩气藏最为有效的方式[8-10]。为此，国内外学者围绕页岩气藏压裂水平井的渗流机理开展了相关研究工作。

分段压裂之后，水平井会产生复杂的裂缝网络，在主裂缝周围会产生许多支缝[11]，如图 1所示。1986年，Lee[12]首次提出了垂直裂缝井三线性流试井模型并得到了解析解。2009年，Brown M[13]建立了多级压裂水平井三线性流模型，如图 2所示，模型假设主裂缝之间的区域均被改造。此后，姚军[14]、高杰[15]分别将此模型应用到低渗透油藏和页岩气藏中，但是三线性流模型仅适用于主裂缝间距较小的情况。而微地震监测表明[16]，水力压裂改造的体积是有限的，当水平井裂缝间距较大时，裂缝之间有部分区域并没有被改造。2012年，Stalgorova[17]建立了如图 3所示的三区复合模型，模型考虑了主裂缝之间未被改造的区域，却忽略了裂缝之外未压裂区对水平井的影响。2013年，Stalgorova[18]在以往研究的基础上，建立了如图 4所示的五区复合模型。2014年，苏玉亮[19]应用此模型对常规油藏进行了产能预测。关于将此模型在页岩气藏中应用的研究还未见报道，为此，本文在Stalgorova建立的五区复合模型的基础上，建立了考虑了页岩气解析、扩散的产能预测模型，并且对模型进行了求解，最后分析了窜流系数、压裂区弹性储容比、水力裂缝导流能力等参数对产能的影响。

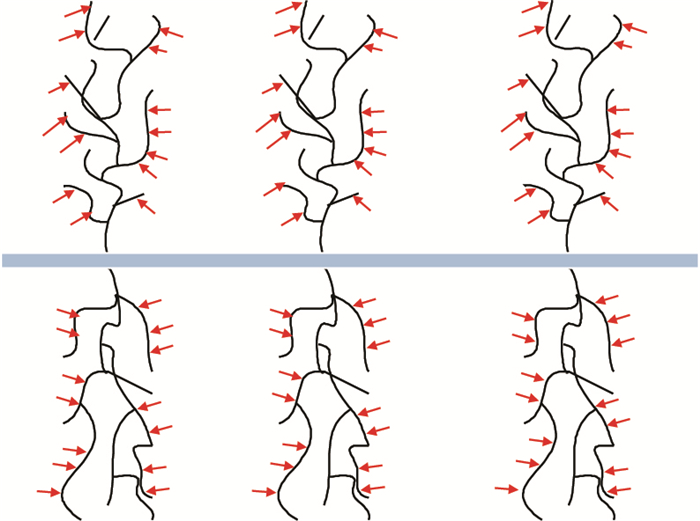图1 压裂水平井示意图 Fig. 1 Schematic diagram for fractured horizontal well
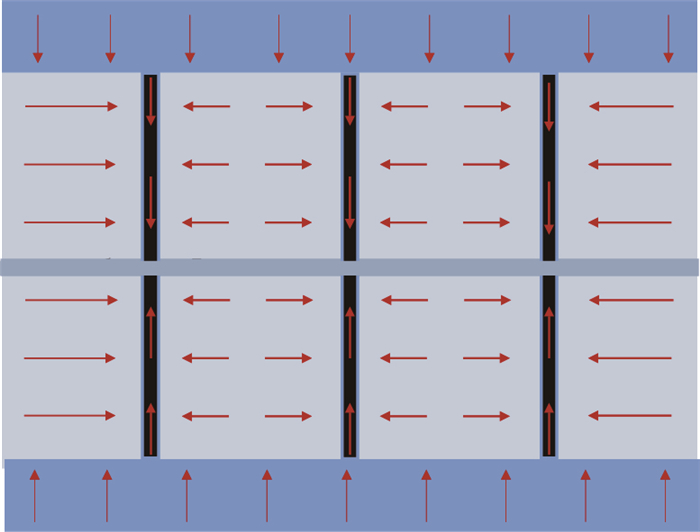图2 Brown三线性流模型图 Fig. 2 Schematic diagram for Brown model of trilinear flow
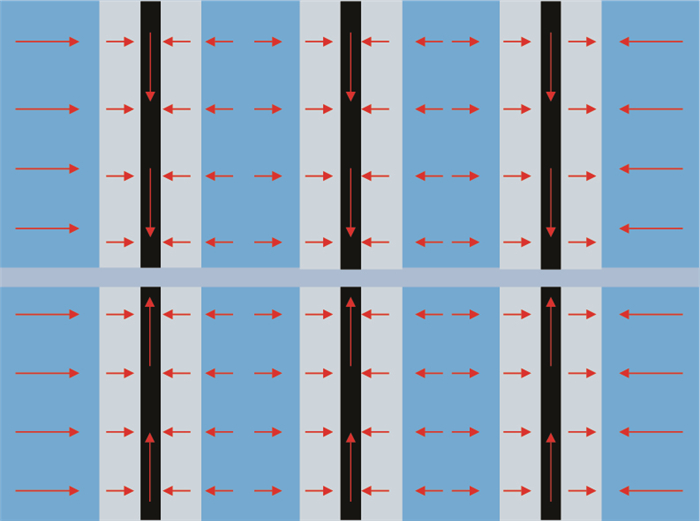图3 Stalgorova三区复合模型图 Fig. 3 Schematic diagram for Stalgorova composite model of three regions
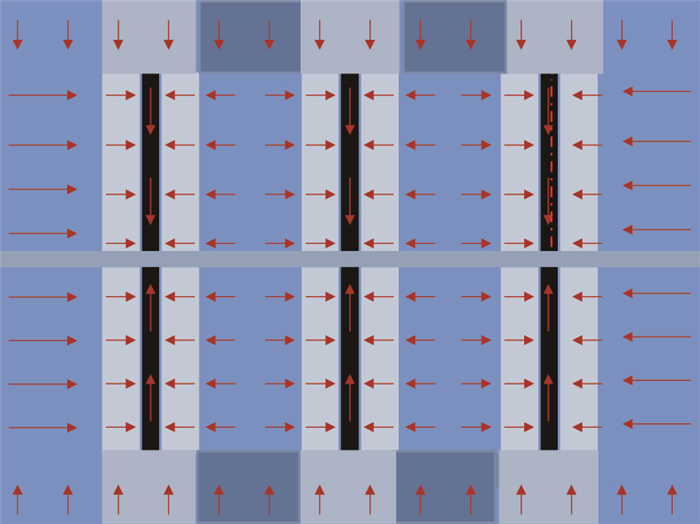图4 Stalgorova五区复合模型图 Fig. 4 Schematic diagram for Stalgorova composite model of five regions
1 五区复合物理模型

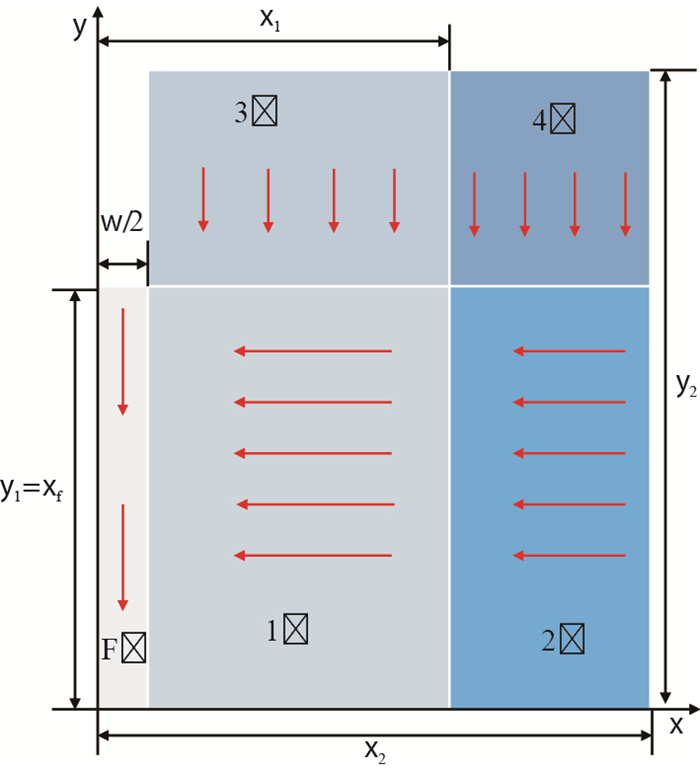
水平井经过压裂之后，主裂缝之间及裂缝之外还有部分区域未被压裂，而几个区域内渗流特征不尽相同，因此，需要对其进行分区。由于对称性，本文只选取了裂缝之间区域的1/4作为压裂水平井五区复合模型物理模型。模型由F区、1区、2区、3区、4区5部分组成。F区为人工裂缝区，1区为压裂改造区，2区、3区和4区为未改造区。3区、4区的流体分别流向1区和2区，2区流体流向1区，1区流体流向人工裂缝，最终人工裂缝内的流体流向井筒，流体在每个区域内都是线性流动。

图5 压裂水平井五区复合模型物理模型 Fig. 5 Physical model of composite model of five regions for fractured horizontal wells

模型假设条件为：(1)人工裂缝沿水平井筒均匀分布，裂缝宽度为w；裂缝半长为xf，缝端封闭；(2)气藏外边界封闭；(3)裂缝完全贯穿储层，裂缝高度等于储层有效厚度；(4)气体流动为单相等温渗流；(5)忽略毛管力和重力影响；(6)储层半宽为y2，压裂裂缝半间距为x2，1、3区x方向宽度为x1，1、2区y方向宽度为y1。

2 五区复合不稳定渗流数学模型

定义如下无因次量：

无因次拟压力：${\psi _{\rm{D}}}=\dfrac{{{\psi _{\rm{i}}} - \psi }}{{{\psi _{\rm{i}}} - {\psi _{{\rm{wf}}}}}}$；

无因次产量：${q_{\rm{D}}}=\frac{{{q_{{\rm{Fsc}}}}\mu {B_{\rm{g}}}}}{{2\pi {K_1}h({\psi _{\rm{i}}} - \psi)}}$；

无因次时间：${t_{\rm{D}}}=\dfrac{{{K_1}t}}{{{\Lambda _1}x_{\rm{f}}^{\rm{2}}}}$；

无因次距离：${x_{\rm{D}}}=\frac{x}{{{x_{\rm{f}}}}}, {y_{\rm{D}}}=\frac{y}{{{x_{\rm{f}}}}}$；

无因次裂缝宽度：${w_{\rm{D}}}=\dfrac{w}{{{x_{\rm{f}}}}}$；窜流系数：$\lambda=\dfrac{{{K_1}\tau }}{{{\Lambda _1}x_{\rm{f}}^{\rm{2}}}}$；

储容比：${\omega _j}=\dfrac{{{\phi _j}\mu {C_{{\rm{t}}j}}}}{{{\Lambda _j}}}$   (j=1，2，3，4)；

无因次裂缝导流能力：${F_{{\rm{CD}}}}=\frac{{{K_{\rm{f}}}w}}{{{K_1}{x_{\rm{f}}}}}$；

无因次储层导流能力：

${R_{{\rm{CD1}}}}=\frac{{{K_2}{x_{\rm{f}}}}}{{{K_4}{y_2}}}, {R_{{\rm{CD2}}}}=\frac{{{K_{\rm{1}}}{x_{\rm{f}}}}}{{{K_{\rm{3}}}{y_2}}}, {R_{{\rm{CD3}}}}=\frac{{{K_{\rm{1}}}{x_{\rm{f}}}}}{{{K_{\rm{2}}}{x_2}}}$

无因次浓度：${V_{j{\rm{D}}}}={V_j} - {V_{\rm{i}}}$   (j=1，2，3，4)；

无因次导压系数：${\eta _{j{\rm{1}}}}=\dfrac{{{\eta _j}}}{{{\eta _1}}}$   (j=F，2，3，4)。

其中：

导压系数：${\eta _j}=\dfrac{{{K_j}}}{{{\phi _j}\mu {C_{{\rm{t}}j}}}}$，  (j=F，1，2，3，4)；

解析时间：$\;\tau=\frac{{{R^2}}}{{6D{\pi ^2}}}$；

拟压力：$\psi(p)=\frac{{{\mu _{\rm{i}}}{Z_{\rm{i}}}}}{{{p_{\rm{i}}}}}\int_{{p_0}}^{{p_{\rm{i}}}} {\frac{p}{{\mu Z}}} {\rm{d}}p$；

${\Lambda _j}={\phi _j}\mu {C_{{\rm{t}}j}}+\dfrac{{{p_{{\rm{sc}}}}T{\mu _{\rm{i}}}{Z_{\rm{i}}}}}{{{K_1}{T_{{\rm{sc}}}}{p_{\rm{i}}}({\psi _{\rm{i}}} - {\psi _{{\rm{wf}}}})}}$(j=1，2，3，4)。

2.1 4区数学模型

由于页岩气藏孔隙度小，页岩对甲烷分子的吸附以单分子层吸附为主，考虑到吸附解析作用的可逆性，因此使用Langmuir等温吸附方程描述页岩气的解吸过程

$ {V_{\rm{E}}}=\frac{{{V_{\rm{L}}}\psi }}{{{\psi _{\rm{L}}}+\psi }} $ (1)

结合式(1)及无因次浓度和无因次拟压力的定义，可得

$ {V_{{\rm{ED}}}}=- \alpha {\psi _{{\rm{1D}}}} $ (2)

式中：α-吸附系数，$\alpha=\dfrac{{{V_{\rm{L}}}{\psi _{\rm{L}}}({\psi _{\rm{i}}} - {\psi _{{\rm{wf}}}})}}{{({\psi _{\rm{L}}}+\tilde{\psi})({\psi _{\rm{L}}}+{\psi _{\rm{i}}})}}$

页岩气由基质扩散到裂缝遵循Fick第一扩散定律，其在无因次下的形式为

$ \dfrac{{\partial {V_{{\rm{4D}}}}}}{{\partial {t_{\rm{D}}}}}=\dfrac{1}{\lambda }({V_{{\rm{ED}}}} - {V_{{\rm{4D}}}}) $ (3)

将运动方程、状态方程代入连续性方程中，同时结合Fick扩散定律，可得4区中渗流控制方程为

$ \frac{{{\partial ^2}{\psi _{{\rm{4D}}}}}}{{\partial y_{\rm{D}}^2}}=\frac{1}{{{\eta _{{\rm{41}}}}}}\left[{{\omega _4}\frac{{\partial {\psi _{{\rm{4D}}}}}}{{\partial {t_{\rm{D}}}}}-(1-{\omega _4})\frac{{\partial {V_{{\rm{4D}}}}}}{{\partial {t_{\rm{D}}}}}} \right] $ (4)

对式(3)、式(4)及定解条件进行Laplace变换，可得4区数学模型为

$ \left\{ \begin{array}{l} \frac{{{\partial ^2}{{\bar \psi }_{{\rm{4D}}}}}}{{\partial y_{\rm{D}}^2}}=\frac{1}{{{\eta _{{\rm{41}}}}}}s{f_4}(s){{\bar \psi }_{{\rm{4D}}}}\\ {{\bar \psi }_{{\rm{4D}}}}{\left| {_{{y_{\rm{D}}}=1\;}\;={{\bar \psi }_{{\rm{2D}}}}} \right|_{{y_{\rm{D}}}=1}}\\ \frac{{\partial {{\bar \psi }_{{\rm{4D}}}}}}{{\partial {y_{\rm{D}}}}}\left| {_{{y_{\rm{D}}}={y_{{\rm{2D}}}}}} \right.=0 \end{array} \right. $ (5)

求解式(5)得到4区压力解表达式为

$ {{\bar \psi }_{{\rm{4D}}}}={{\bar \psi }_{{\rm{2D}}}}\left| {{y_{\rm{D}}}=1} \right.\frac{{\cosh \left[{\sqrt {\frac{{s{f_4}(s)}}{{{\eta _{{\rm{41}}}}}}(} {y_{{\rm{2D}}}}-{y_{\rm{D}}})} \right]}}{{\cosh \left\lfloor {\sqrt {\frac{{s{f_4}(s)}}{{{\eta _{{\rm{41}}}}}}(} {y_{{\rm{2D}}}} - 1)} \right\rfloor }} $ (6)

式中：

$ {f_4}(s)={\omega _4}+\dfrac{{\alpha(1 - {\omega _4})}}{{1+\lambda s}} $
2.2 3区数学模型

3区也为沿y方向的线性流动，根据外边界封闭及3区与2区交界处压力连续的条件，可得3区数学模型为

$ \left\{ \begin{array}{l} \frac{{{\partial ^2}{{\bar \psi }_{{\rm{3D}}}}}}{{\partial y_{\rm{D}}^2}}=\frac{1}{{{\eta _{{\rm{31}}}}}}s{f_3}(s){{\bar \psi }_{{\rm{3D}}}}\\ {{\bar \psi }_{{\rm{3D}}}}{\left| {_{{y_{\rm{D}}}=1}={{\bar \psi }_{{\rm{1D}}}}} \right|_{{y_{\rm{D}}}=1}}\\ \frac{{\partial {{\bar \psi }_{{\rm{3D}}}}}}{{\partial {y_{\rm{D}}}}}\left| {_{{y_{\rm{D}}}={y_{{\rm{2D}}}}}} \right.=0 \end{array} \right.\; $ (7)

将式(6)代入式(7)，可得3区压力解表达式为

$ {{\bar \psi }_{{\rm{3D}}}}={{\bar \psi }_{{\rm{1D}}}}\left| {_{{y_{\rm{D}}}=1}} \right.\frac{{\cosh \left[{\sqrt {\frac{{s{f_3}(s)}}{{{\eta _{{\rm{31}}}}}}}({y_{\rm{D}}}-{y_{{\rm{2D}}}})} \right]}}{{\cosh \left[{\sqrt {\frac{{s{f_3}(s)}}{{{\eta _{{\rm{31}}}}}}}(1-{y_{{\rm{2D}}}})} \right]}} $ (8)

式中：

$ {f_3}(s)={\omega _3}+\frac{{\alpha(1 - {\omega _3})}}{{1+\lambda s}}. $
2.3 2区数学模型

2区为沿着x方向的线性流动，根据外边界封闭条件及2区与1区交界面处压力连续的条件，可得2区数学模型为

$ \left\{ \begin{array}{l} \frac{{{\partial ^2}{{\bar \psi }_{{\rm{2D}}}}}}{{\partial x_{\rm{D}}^2}}+\frac{1}{{{R_{{\rm{CD1}}}}{y_{{\rm{2D}}}}}}\frac{{\partial {{\bar \psi }_{{\rm{4D}}}}}}{{\partial {y_{\rm{D}}}}}\left| {_{{y_{\rm{D}}}=1}} \right.=\frac{1}{{{\eta _{{\rm{21}}}}}}s{f_2}(s){{\bar \psi }_{{\rm{2D}}}}\\ {{\bar \psi }_{{\rm{2D}}}}\left| {_{{x_{\rm{D}}}={x_{{\rm{1D}}}}}} \right.={{\bar \psi }_{{\rm{1D}}}}\left| {_{{x_{\rm{D}}}={x_{{\rm{1D}}}}}} \right.\\ \frac{{\partial {{\bar \psi }_{{\rm{2D}}}}}}{{\partial {x_{\rm{D}}}}}\left| {_{{x_{\rm{D}}}={x_{{\rm{2D}}}}}} \right.=0 \end{array} \right.\;\; $ (9)

将式(8)代入式(9)，可得2区压力解表达式为

$ {{\bar \psi }_{{\rm{2D}}}}={{\bar \psi }_{{\rm{1D}}}}\left| {_{{x_{\rm{D}}}={x_{{\rm{1D}}}}}} \right.\frac{{\cosh \left[{\sqrt {{c_1}(} {x_{{\rm{2D}}}}-{x_{\rm{D}}})} \right]}}{{\cosh \left\lfloor {\sqrt {{c_1}(} {x_{{\rm{2D}}}} - {x_{{\rm{1D}}}})} \right\rfloor }} $ (10)

式中：${f_2}(s)={\omega _2}+\dfrac{{\alpha(1 - {\omega _2})}}{{1+\lambda s}}$；

$ \begin{array}{l} {c_1}=\frac{{s{f_2}(s)}}{{{\eta _{{\rm{21}}}}}}+\\ \;\;\;\;\;\frac{1}{{{R_{{\rm{CD1}}}}{y_{{\rm{2D}}}}}}\sqrt {\frac{{s{f_4}(s)}}{{{\eta _{{\rm{41}}}}}}} \tanh \left[{\sqrt {\frac{{s{f_4}(s)}}{{{\eta _{{\rm{41}}}}}}(} {y_{{\rm{2D}}}}-1)} \right]. \end{array} $
2.4 1区数学模型

1区为沿着x方向的线性流动，根据2区与1区交界面处流量连续及1区与人工裂缝区交界面处压力连续的条件，可得1区数学模型为

$ \left\{ \begin{array}{l} \frac{{{\partial ^2}{{\bar \psi }_{{\rm{1D}}}}}}{{\partial x_{\rm{D}}^2}}+\frac{1}{{{R_{{\rm{CD2}}}}{y_{{\rm{2D}}}}}}\frac{{\partial {{\bar \psi }_{{\rm{3D}}}}}}{{\partial {y_{\rm{D}}}}}\left| {_{{y_{\rm{D}}}=1}} \right.=s{f_1}(s){{\bar \psi }_{{\rm{1D}}}}\\ {{\bar \psi }_{{\rm{1D}}}}\left| {_{{x_{\rm{D}}}={w_{\rm{D}}}/2}} \right.={{\bar \psi }_{{\rm{FD}}}}\left| {_{{x_{\rm{D}}}={w_{\rm{D}}}/2}} \right.\\ \frac{{\partial {{\bar \psi }_{{\rm{1D}}}}}}{{\partial {x_{\rm{D}}}}}\left| {_{{x_{\rm{D}}}={x_{{\rm{1D}}}}}} \right.=\frac{1}{{{R_{{\rm{CD3}}}}{x_{{\rm{2D}}}}}}\frac{{\partial {{\bar \psi }_{{\rm{2D}}}}}}{{\partial {x_{\rm{D}}}}}\left| {_{{x_{\rm{D}}}={x_{{\rm{1D}}}}}} \right. \end{array} \right.\;\;\; $ (11)

将式(10)代入式(11)，可得1区压力解表达式如式(12)所示。

$ {{\bar \psi }_{{\rm{1D}}}}={{\bar \psi }_{{\rm{FD}}}}\left| {_{{x_{\rm{D}}}={w_{\rm{D}}}/2}} \right.\frac{{{c_3}\sinh \left[{\sqrt {{c_2}}({x_{\rm{D}}}-{x_{{\rm{1D}}}})} \right]+\cosh \left[{\sqrt {{c_2}}({x_{\rm{D}}}-{x_{{\rm{1D}}}})} \right]}}{{{c_4}}} $ (12)

式中：${f_1}(s)={\omega _1}+\dfrac{{\alpha(1 - {\omega _1})}}{{1+\lambda s}}$；

$ \begin{array}{l} {c_2}=\frac{1}{{{R_{{\rm{CD2}}}}{y_{{\rm{2D}}}}}}\sqrt {\frac{{s{f_3}(s)}}{{{\eta _{{\rm{31}}}}}}} \tanh \left[{\sqrt {\frac{{s{f_3}(s)}}{{{\eta _{{\rm{31}}}}}}(} {y_{{\rm{2D}}}}-1)} \right]+\\ s{f_1}(s)\\ {c_3}=\frac{1}{{{R_{{\rm{CD3}}}}{x_{{\rm{2D}}}}}}\sqrt {\frac{{{c_1}}}{{{c_2}}}} \tanh \left[{\sqrt {{c_1}(} {x_{{\rm{1D}}}}-{x_{{\rm{2D}}}})} \right];\\ {c_4}={c_3}\sinh \left[{\sqrt {{c_2}}(\frac{{{w_{\rm{D}}}}}{2}-{x_{{\rm{1D}}}})} \right]+\\ \cosh \left[{\sqrt {{c_2}}(\frac{{{w_{\rm{D}}}}}{2}-{x_{{\rm{1D}}}})} \right]. \end{array} $
2.5 人工裂缝区模型

人工裂缝区为沿着y方向的线性流动，根据缝端封闭条件及井底定压条件，结合达西定律，可得人工裂缝区数学模型为

$ \left\{ \begin{array}{l} \frac{{{\partial ^2}{{\bar \psi }_{{\rm{FD}}}}}}{{\partial {y_{\rm{D}}}^2}}+\frac{2}{{{F_{{\rm{CD}}}}}}\frac{{\partial {{\bar \psi }_{{\rm{2D}}}}}}{{\partial {x_{\rm{D}}}}}\left| {_{{x_{\rm{D}}}=\frac{{{w_{\rm{D}}}}}{2}}} \right.=\frac{s}{{{\eta _{{\rm{F1}}}}}}{{\bar \psi }_{{\rm{FD}}}}\\ {{\bar \psi }_{{\rm{FD}}}}\left| {_{{y_{\rm{D}}}=0}} \right.=1\\ \frac{{\partial {{\bar \psi }_{{\rm{FD}}}}}}{{\partial {y_{\rm{D}}}}}\left| {_{{y_{\rm{D}}}=1}} \right.=0 \end{array} \right.\; $ (13)

将式(12)代入式(13)，可得F区压力解表达式

$ {{\bar \psi }_{{\rm{FD}}}}=\frac{{\cosh \left[{\sqrt {{c_6}}(1-{y_{\rm{D}}})} \right]}}{{s\cosh(\sqrt {{c_6}})}} $ (14)

式中：

$ \begin{array}{l} {c_5}=\sqrt {{c_2}} \frac{{{c_3}\cosh \left[{\sqrt {{c_2}} \left({\frac{{{w_{\rm{D}}}}}{2}-{x_{{\rm{1D}}}}} \right)} \right]+\sinh \left[{\sqrt {{c_2}} \left({\frac{{{w_{\rm{D}}}}}{2}-{x_{{\rm{1D}}}}} \right)} \right]}}{{{c_4}}};\\ {c_6}=\frac{s}{{{\eta _{{\rm{F1}}}}}} - \frac{2}{{{F_{{\rm{CD}}}}}}{c_5}. \end{array} $

根据达西定律，当yD=0时，求得产能公式为

$ {\bar q_{{\rm{FD}}}}=\frac{{{F_{{\rm{CD}}}}\sqrt {{c_6}} \tanh \sqrt {{c_6}} }}{{s\pi }} $ (15)

根据式(15)，可以求得Laplace空间中的无因次产量，通过Stehfest数值反演技术[20]可以得到在实空间中的产量解。

3 产能递减曲线及影响因素分析

计算参数取值：

ω1=0.02，ω2=ω3=ω4=0.01，λ=150，FCD=100，x1D=1.2，x2D=1.5，y1D=1，y2D=1.2，η41=η31=η21=0.1，ηF1=100，K2/K1=K3/K1=0.1，K4/K2=1，α=5，由此计算出RCD1=0.83，RCD2=8.33，RCD3=6.67。

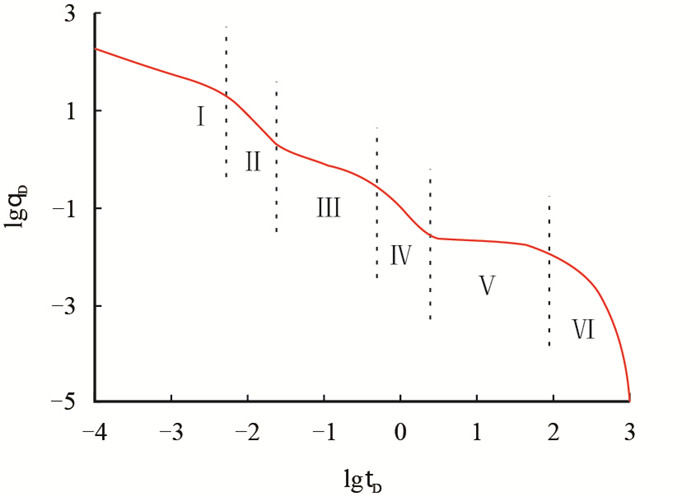
图 6反映了页岩气藏多级压裂水平井生产过程中各个流动阶段的产量递减特征。从图中可以看出，产能递减曲线主要分为6个流动阶段。Ⅰ为主裂缝线性流动阶段，其特点为在双对数曲线上斜率为0.5，持续时间不长，在实际生产中很难被监测到；Ⅱ为主裂缝边界影响与压裂区供气复合流动阶段，其特点是在双对数曲线上斜率为1左右；Ⅲ为1区和2区线性流动阶段，其特点为在双对数曲线上斜率为0.5；Ⅳ为2区边界影响和3区与4区供气阶段，其特点是在双对数曲线上斜率为1左右；Ⅴ为页岩气的解吸扩散阶段，随着气藏压力的降低，吸附在页岩基质表面的页岩气发生解吸，然后扩散进入裂缝，此阶段的特点是曲线缓慢下降，这也是页岩气藏具有较长稳产期的原因；Ⅵ为3区与4区的外边界反应阶段，压力传播到达封闭外边界后，没有充足的气源供给，产量迅速下降。

图6 产能递减曲线不同流动阶段的划分 Fig. 6 The division of different seepage stages on the production decline curves

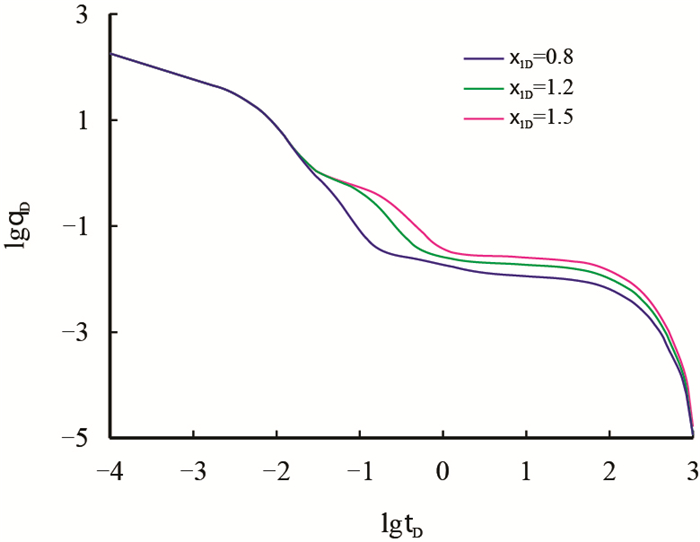
图 7对比了不同压裂区宽度(x1D)对产能递减曲线的影响。计算过程中，保持裂缝间距(x2D)不变，只改变x1D的数值。从图中可以看出，压裂区宽度主要对主裂缝线性流动以后的阶段产生影响，x1D越大，压裂区供气能力就越强，产能就越大。x1D=1.5时，五区复合模型就变成了三线性流模型，因此，使用三线性流模型进行产能预测时预测结果相对本文五区复合模型会偏高。

图7 x1D对产能递减曲线的影响 Fig. 7 The effect of x1D on the production decline curves

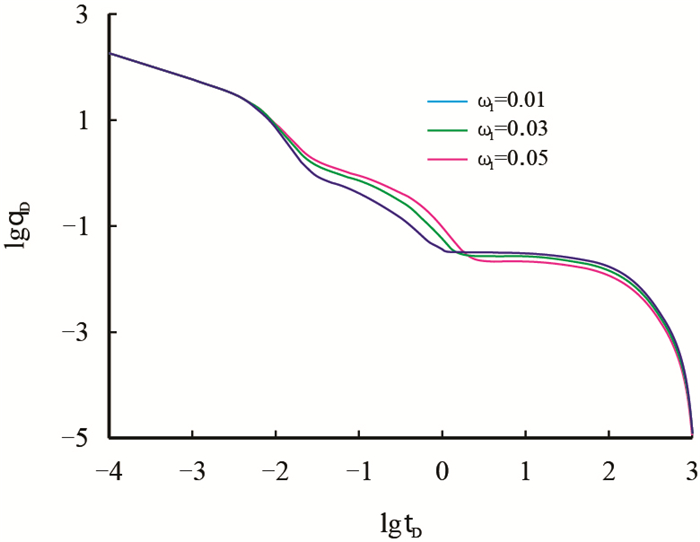
图 8对比了不同的1区弹性储容比时的产能递减曲线。从图中可以看到，1区弹性储容比主要影响1区和2区的线性流动及2区边界影响阶段，储容比越大，线性流动持续的时间越长，产量越大，递减速度越慢。这是因为，根据1区弹性储容比的定义，此阶段的气体主要来自裂缝系统的游离气，储容比越大，裂缝系统中储存着越多的气体，因此产量也越大，随着气体源源不断地供给，递减速度也越慢，但后期由于页岩基质吸附气的解吸扩散，储容比的作用就会逐渐减弱直至消失。

图8 ω1对产能递减曲线的影响 Fig. 8 The effect of ω1 on the production decline curves

图 9反映了不同窜流系数下的产能递减曲线。从中可以看出，窜流系数主要影响解吸扩散及以后的流动阶段，对前期的产量并没有影响。窜流系数越大，解吸扩散阶段开始及结束的时间越早，解吸扩散阶段的产量越高，后期产量就越低。这是因为，根据窜流系数的定义可知，窜流系数反映了解吸时间的早晚，解吸时间越早，窜流系数就越小，因此发生解吸扩散的时间越早，由于解析气的供给，产量递减越慢，产量越高，但是气体总量是一定的，解吸扩散阶段产能越大，后期产能就越小，产量递减就越快。

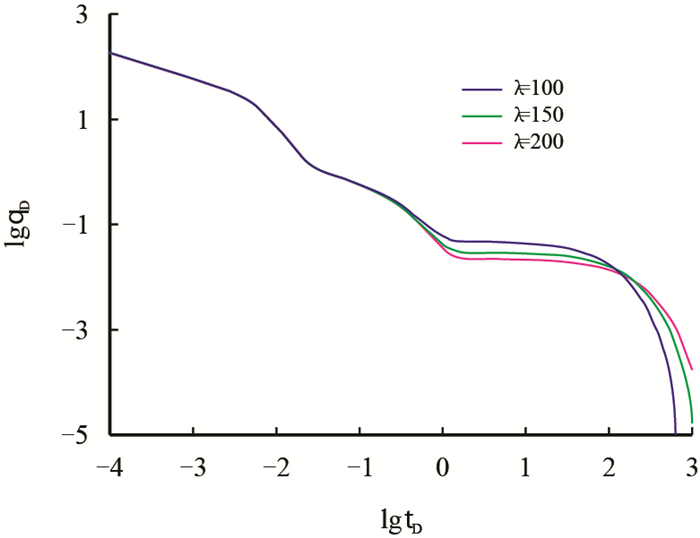图9 λ对产能递减曲线的影响 Fig. 9 The effect of λ on the production decline curves

图 10反映了不同裂缝导流能力下的产能递减曲线。从图中可以看出，导流能力主要影响早期裂缝线性流动阶段，随着时间的增加，其影响作用逐渐消失。导流能力越小，裂缝线性流持续的时间越长，无因次产量也越小；反之，导流能力越大，裂缝线性流持续的时间越短，无因次产量也越大。

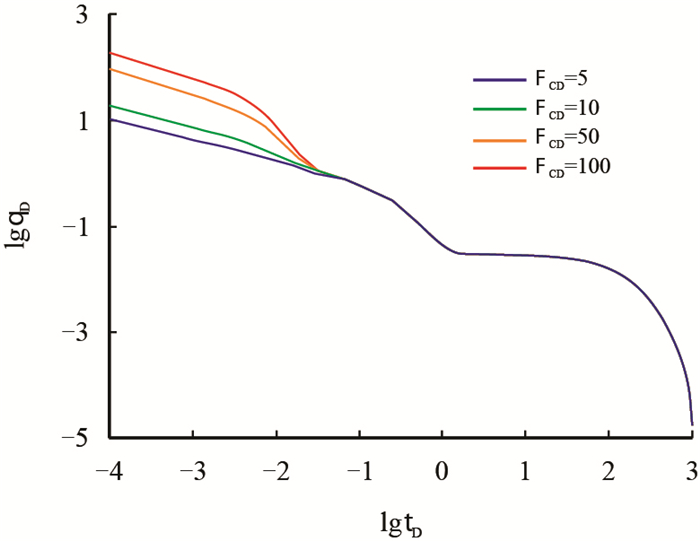图10 FCD对产能递减曲线的影响 Fig. 10 The effect of FCD on the production decline curves

图 11反映了1区渗透率不同情况下的产能递减曲线假设(β=K1/K2)。从图中可以看出，1区渗透率主要对中后期的产能曲线产生影响，渗透率越大，产能越大，这是因为1区渗透率越大，说明压裂之后形成的缝网与天然微裂缝沟通的越好，整个裂缝系统的导流能力越大，气体渗流阻力就越小，因此产能也就越大。

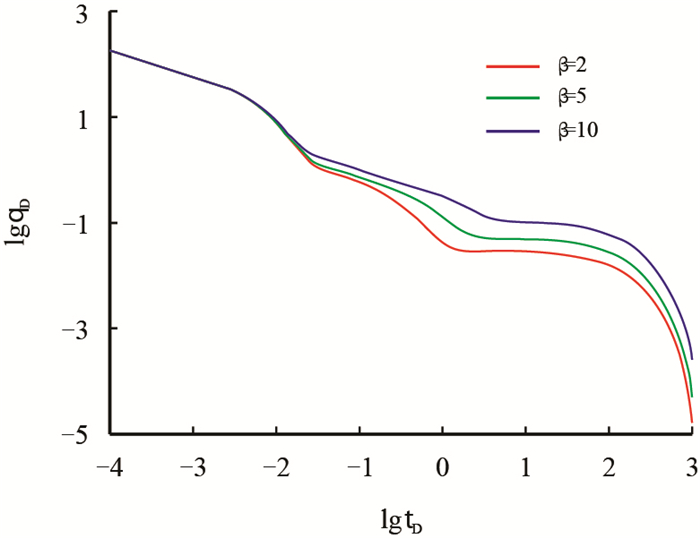图11 β对产能递减曲线的影响 Fig. 11 The effect of β on the production decline curves
4 结论

(1)建立并求解了综合考虑页岩气解吸、扩散和渗流特征的页岩气藏压裂水平井五区复合渗流模型，绘制并分析了产能递减曲线。

(2)页岩气藏压裂水平井产能递减曲线可以分为6个流动阶段：主裂缝线性流动阶段、主裂缝边界影响与压裂区供气复合流动阶段、1区和2区线性流动阶段、2区边界影响和3区与4区供气阶段、解吸扩散阶段和3区与4区的外边界反应阶段。

(3)1区弹性储容比主要影响1区和2区的线性流动及2区边界影响阶段，储容比越大，线性流动持续的时间越长，产量越大，递减速度越慢。窜流系数主要影响解吸扩散及以后的流动阶段，窜流系数越大，解吸扩散阶段开始及结束的时间越早，解吸扩散阶段的产量越高，后期产量就越低。

(4)主裂缝导流能力主要影响早期裂缝线性流动阶段，导流能力越小，裂缝线性流持续的时间越长，无因次产量也越小。1区渗透率主要对中后期的产能曲线产生影响，渗透率越大，压裂之后形成的缝网与天然微裂缝沟通的越好，产能越大。压裂区宽度主要对主裂缝线性流动以后的阶段产生影响，宽度越大，产能就越大。

符号说明

ψi-原始条件下的拟压力，Pa；

ψ-拟压力，Pa；

ψwf-井底拟压力，Pa；

qFsc-标况下每条裂缝的产量，m3/s；

µ-页岩气黏度，Pa·s；

Bg页岩气体积系数，无因次；

K1，K2，K3，K4-1区、2区、3区和4区的渗透率，D；

h-页岩气储层厚度，m；

t-时间，s；

xf裂缝半长，m；

x，y-距离，m；

w-裂缝宽度，m；

λ-窜流系数，无因次；

τ解析时间，s；

ω j-j区的储容比，无因次；

ϕ j-j区的孔隙度，无因次；

Vtj-j区的综合压缩系数，Pa−1；

Kf-j区水力裂缝区渗透率，D；

VjD-j区的无因次页岩气浓度，m3/m3；

Vj-j区的页岩气浓度，m3/m3；

Vi-j区原始条件下的页岩气浓度，m3/m3；

η j1-j区的无因次导压系数；

η j-j区的导压系数，m2·Pa/（Pa·s）；

r-页岩气基质岩块半径，m；

D-页岩气扩散系数，m2/s；

µi-原始条件下的页岩气黏度，Pa·s；

Zi-原始条件下的页岩气偏差因子，无因次；

pi-原始条件下的页岩气储层压力，Pa；

p0-参考压力，Pa；

p-页岩气储层压力，Pa；

Z-页岩气偏差因子，无因次；

psc-标准状况下的压力，Pa；

T-页岩气储层温度，K；

Tsc标准状况下的温度，K；

VE-等温吸附量，m3/m3；

VL-Langmuir体积，m3/m3；

ψL-Langmuir压力，Pa；

VED-无因次等温吸附量；

α-吸附系数，无因次；

ψFD，ψ1D，ψ2D，ψ3D，ψ4D-F区、1区、2区、3区和4区的无因次拟压力；

$\tilde \psi $-地层平均拟压力，Pa；

${\bar \psi _{{\rm{FD}}}}, {\bar \psi _{{\rm{1D}}}}, {\bar \psi _{{\rm{2D}}}}, {\bar \psi _{{\rm{3D}}}}, {\bar \psi _{{\rm{4D}}}}$-拉氏空间中F区、1区、2区、3区和4区的无因次拟压力；

s-拉氏因子，无因次；

RCD1，RCD2，RCD3-1区、2区和3区无因次储层导流能力；

x1D，x3D-1区和3区x 方向的无因次宽度、压裂裂缝无因次半间距；

y1D，y2D-1区和2区y方向无因次宽度、储层无因次半宽；

下标D-无因次；

下标F，1，2，3，4 -水力裂缝、1区、2区、3区和4区的相关参数。

参考文献
[1] 江怀友, 鞠斌山, 李治平, 等. 世界页岩气资源现状研究[J]. 中外能源, 2014, 19 (3) : 14 –22.
Jiang Huaiyou, Ju Binshan, Li Zhiping, et al. The world's shale gas resources today[J]. Sino-Global Energy, 2014, 19 (3) : 14 –22.
[2] 滕吉文, 刘有山. 中国油气页岩分布与存储潜能和前景分析[J]. 地球物理学进展, 2013, 28 (3) : 1083 –1108.
Teng Jiwen, Liu Youshan. Analysis of distribution, storage potential and prospect for shale oil and gas in China[J]. Progress in Geophysics, 2013, 28 (3) : 1083 –1108.
[3] 于荣泽, 张晓伟, 卞亚南. 页岩气藏流动机理与产能影响因素分析[J]. 天然气工业, 2012, 32 (9) : 10 –15.
Yu Rongze, Zhang Xiaowei, Bian Yanan. Flow mechanism of shale gas reservoirs and influential factors of their productivity[J]. Natural Gas Industry, 2012, 32 (9) : 10 –15.
[4] Vassilellis G D, Li C, Seager R, et al. Investigating the expected long-term production performance of shale reservoirs[C]. SPE 138134, 2010.
[5] 任岚, 舒亮, 胡永全, 等. 纳米尺度页岩储层的气体流动行为分析[J]. 西南石油大学学报:自然科学版, 2014, 36 (5) : 111 –116.
Ren Lan, Shu Liang, Hu Yongquan, et al. Analysis of gas flow behavior in nano-scale shale gas reservoir[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2014, 36 (5) : 111 –116.
[6] 任建华, 蔺景德, 张亮, 等. 页岩气藏吸附特征及其对产能的影响[J]. 新疆石油地质, 2013, 34 (4) : 441 –444.
Ren Jianhua, Lin Jingde, Zhang Liang, et al. Adsorption characteristics and impact on productivity of shale gas reservoir[J]. Xinjiang Petroleum Geology, 2013, 34 (4) : 441 –444.
[7] 侯读杰, 包书景, 毛小平, 等. 页岩气资源潜力评价的几个关键问题讨论[J]. 地球科学与环境学报, 2012, 34 (3) : 7 –16.
Hou Dujie, Bao Shujing, Mao Xiaoping, et al. Discussion on the key issues of resource potential evaluation for shale gas[J]. Journal of Earth Sciences and Environment, 2012, 34 (3) : 7 –16.
[8] 琚宜文, 卜红玲, 王国昌. 页岩气储层主要特征及其对储层改造的影响[J]. 地球科学进展, 2014, 29 (4) : 492 –506.
Ju Yiwen, Bu Hongling, Wang Guochang. Main characteristics of shale gas reservoir and its effect on the reservoir reconstruction[J]. Advances in Earth Science, 2014, 29 (4) : 492 –506.
[9] 张小涛, 吴建发, 冯曦, 等. 页岩气藏水平井分段压裂渗流特征数值模拟[J]. 天然气工业, 2013, 33 (3) : 47 –52.
Zhang Xiaotao, Wu Jianfa, Feng Xi, et al. Numerical simulation of seepage flow characteristics of multi-stage fracturing(MSF)in horizontal shale gas wells[J]. Natural Gas Industry, 2013, 33 (3) : 47 –52.
[10] 王妍, 高文冰. 国内外页岩气勘探与开发技术分析[J]. 地下水, 2014, 36 (2) : 205 –208.
Wang Yan, Gao Wenbing. Exploration and exploitation technical analysis in shale gas reservoir at home and abroad[J]. Ground Water, 2014, 36 (2) : 205 –208.
[11] 赵金洲, 任岚, 胡永全. 页岩储层压裂缝成网延伸的受控因素分析[J]. 西南石油大学学报:自然科学版, 2013, 35 (1) : 1 –9.
Zhao Jinzhou, Ren Lan, Hu Yongquan. Controlling factors of hydraulic fractures extending into network in shale formations[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2013, 35 (1) : 1 –9.
[12] Lee, Brockenbrough. A new approximate analytic solution for finite-conductivity vertical fractures[C]. SPE 12013, 1986.
[13] Brown M, Ozkan E, Raghavan R, et al. Practical solutions for pressure transient responses of fractured horizontal wells in unconventional reservoirs[C]. SPE 125043, 2009.
[14] 姚军, 殷修杏, 樊冬艳, 等. 低渗透油藏的压裂水平井三线性流试井模型[J]. 油气井测试, 2011, 20 (5) : 1 –5.
Yao Jun, Yin Xiuxing, Fan Dongyan, et al. Trilinear-flow well test model of fractured horizontal well in low permeability reservoir[J]. Well Testing, 2011, 20 (5) : 1 –5.
[15] 高杰, 张烈辉, 刘启国, 等. 页岩气藏压裂水平井三线性流试井模型研究[J]. 水动力学研究与进展:A辑, 2014, 29 (1) : 108 –113.
Gao Jie, Zhang Liehui, Liu Qiguo, et al. Well test model of trilinear flow for fractured horizontal wells in shale gas reservoirs[J]. Chinese Journal of Hydrodynamics, 2014, 29 (1) : 108 –113.
[16] Maxwell S C. What does microseismicity tells us about hydraulic fractures[C]. SPE 146932, 2011.
[17] Stalgorova, Associates, Matter, et al. Practical analytical model simulate production of horizontal wells with branch fractures[C]. SPE 162515, 2012.
[18] Stalgorova, Matter. Analytical model for Unconventional Multifractured composite systems[C]. SPE 162516, 2013.
[19] 苏玉亮, 王文东, 盛广龙. 体积压裂水平井复合流动模型[J]. 石油学报, 2014, 35 (3) : 504 –510.
Su Yuliang, Wang Wendong, Sheng Guanglong. Compound flow model of volume fractured horizontal well[J]. Acta Petrolei Sinica, 2014, 35 (3) : 504 –510.
[20] 同登科, 陈钦雷. 关于Laplace数值反演Stehfest方法的一点注记[J]. 石油学报, 2001, 22 (6) : 91 –92.
Tong Dengke, Chen Qinlei. A note of Laplace numerical inversion for Stehfest method[J]. Acta Petrolei Sinica, 2001, 22 (6) : 91 –92.