2. 中国石油长庆油田勘探开发研究院, 陕西 西安 710021
2. Exploration & Development Research Institue, Changqing Oilfield Company, PetroChina, Xi'an, Shaanxi 710021, China
定向井、大斜度井开发致密气藏时,为获得较高产量,通常在射孔段进行水力压裂[1-3]。由于井筒倾斜及钻完井对近井地应力场的改变等因素,压裂缝通常与垂向存在一定夹角,即形成了倾斜缝。国内外学者[4-8]对斜井筒压裂工艺及倾斜缝的产生机理进行了大量研究,但目前压裂倾斜缝的压力动态研究非常少。
Cinco L H[9]利用Green函数和Newman乘积原理推导了倾斜板源函数,得到了无限导流倾斜缝的井底压力解析解,同时将其流动阶段划分为线性流、过渡流和拟径向流。Dinh A V[10]扩展了Cinco L H[9]解析解,详细地讨论了裂缝无限导流下的压力响应特征,给出了各流动阶段的井底压力解析表达式。以上方法均是假设裂缝为无限导流。实际中,缝内往往存在压力损耗,即裂缝有限导流。忽略裂缝的有限导流能力将对试井分析及压后效果评价产生较大误差。
本文将压裂倾斜缝离散为若干微元,结合Darcy公式描述了缝内流动,通过耦合气藏流动建立了倾斜缝不稳定流动模型。利用该模型计算了井底压力曲线,划分了流动阶段,分析了气藏及裂缝参数对压力动态的影响,并进行了实例研究。
1 物理模型在均质、各向异性、上下封闭无界气藏中,处在生产段的倾斜井筒压裂后形成图 1所示的倾斜缝。压裂缝贯穿储层,横向延伸方向为水平最大主应力方向,纵向沿井筒方向。地层及流体均微可压缩,且压缩系数为常数。单相气体在地层中的流动服从不稳定渗流。不考虑重力的影响。
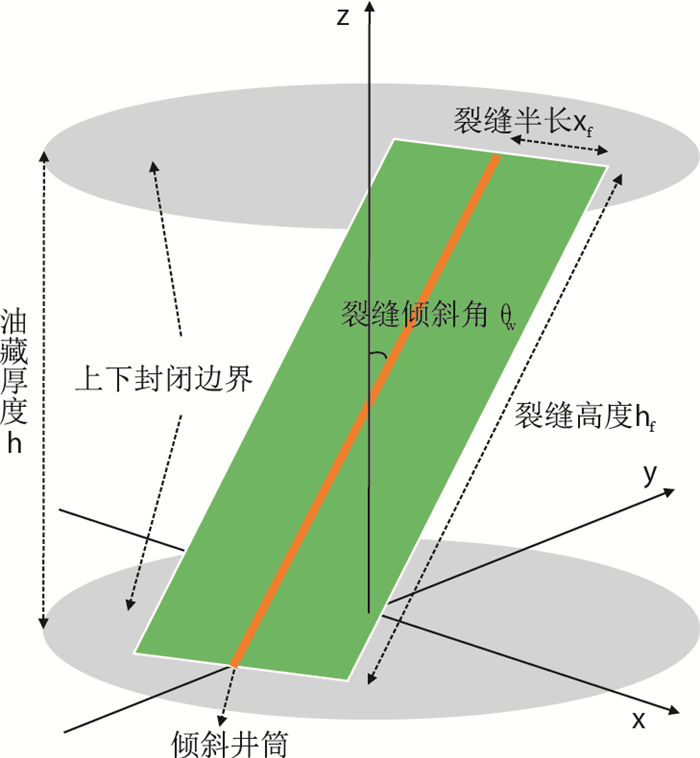 |
| 图1 压裂倾斜缝示意图 Fig. 1 An inclined fracture fully penetrating infinite slab reservoir |
将该裂缝离散为2
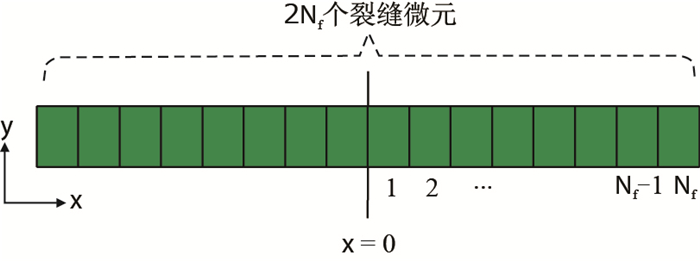 |
| 图2 离散裂缝微元 Fig. 2 Discrete fracture segments |
地层流体从储层流向井筒过程中,会存在气藏流动和裂缝内部流动。以下分别对该两种流动过程建模,再在裂缝面进行压力和流量耦合,从而建立倾斜缝流动模型。对于气体流动,还需引入拟压力函数[11]
| $ m(p) = 2\int\limits_{{p_0}}^p {\dfrac{p}{{\mu Z}}{\rm{d}}p} $ | (1) |
定义无因次拟压力、无因次流量、无因次时间及裂缝各无因次参数如下
| ${m_{{\rm{wD}}}} = \dfrac{{{K_{\rm{h}}}h\sqrt {{K_{\rm{h}}}/{K_{\rm{v}}}} \left[{m({p_{\rm{i}}})-m({p_{\rm{w}}})} \right]}}{{1.291 \times {{10}^{ - 3}}{q_{\rm{w}}}T}};$ |
| ${q_{{\rm{fD}}i}} = \dfrac{{2{x_{\rm{f}}} \cdot {q_{{\rm{f}}i}}}}{{{q_{\rm{w}}}{B_{\rm{g}}}}};$ |
| ${m_{{\rm{fD}}i}} = \dfrac{{{K_{\rm{h}}}h\sqrt {{K_{\rm{h}}}/{K_{\rm{v}}}} \left[{m({p_i})-m({p_{{\rm{f}}i}})} \right]}}{{1.291 \times {{10}^{ - 3}}{q_{\rm{w}}}T}};$ |
| ${t_{\rm{D}}} = \dfrac{{3.6{K_{\rm{h}}}t}}{{\phi \mu {c_{\rm{t}}}x_{\rm{f}}^2}};$ |
| $ {F_{\rm{D}}} = \dfrac{{{K_{\rm{f}}}w{}_{\rm{f}}}}{{{K_{\rm{h}}}{x_{\rm{f}}}}}; $ |
| ${h_{{\rm{fD}}}} = \dfrac{{{h_{\rm{f}}}}}{{{x_{\rm{f}}}}}\sqrt {\dfrac{{{K_{\rm{h}}}}}{{{K_{\rm{v}}}}}{{\cos }^2}{\theta _{\rm{w}}} + {{\sin }^2}{\theta _{\rm{w}}}};$ |
| $\theta _{\rm{w}}^{\rm{'}} = {\tan ^{ - 1}}\left( {\sqrt {\dfrac{{{K_{\rm{v}}}}}{{{K_{\rm{h}}}}}} \cdot \tan {\theta _{\rm{w}}}} \right);$ |
| ${x_{\rm{D}}} = \dfrac{x}{{{x_{\rm{f}}}}};$ |
| ${y_{\rm{D}}} = \dfrac{y}{{{x_{\rm{f}}}}};$ |
| ${z_{\rm{D}}} = \dfrac{z}{{{x_{\rm{f}}}}}\sqrt {\dfrac{{{K_{\rm{h}}}}}{{{K_{\rm{v}}}}}} ;$ |
| ${z_{{\rm{fD}}}} = \dfrac{{{z_{\rm{f}}}}}{{{x_{\rm{f}}}}}\sqrt {\dfrac{{{K_{\rm{h}}}}}{{{K_{\rm{v}}}}}} ;$ |
| ${h_{\rm{D}}} = \dfrac{h}{{{x_{\rm{f}}}}}\sqrt {\dfrac{{{K_{\rm{h}}}}}{{{K_{\rm{v}}}}}{{\cos }^2}{\theta _{\rm{w}}} + {{\sin }^2}{\theta _{\rm{w}}}} 。$ |
根据国内学者[12-14]的研究,裂缝内线性不稳定流动方程为
| $ \dfrac{{{\partial ^2}m({p_{\rm{f}}})}}{{\partial {x^2}}} + \dfrac{{{q_{\rm{f}}}}}{{{K_{\rm{f}}}{w_{\rm{f}}} \cdot {h_{\rm{f}}}}}\dfrac{{{p_{\rm{f}}}}}{z} = \dfrac{{{\phi _{\rm{f}}}\mu {c_{{\rm{ft}}}}}}{{{K_{\rm{f}}}}}\dfrac{{\partial m({p_{\rm{f}}})}}{{\partial t}} $ | (2) |
虽然对缝内进行不稳定流动建模可提高计算精度,但在流动早期,由于不稳定流动形成的裂缝线性流持续时间非常短,对试井分析意义不大。假设裂缝内为稳定流且足以满足压力分析的精度要求[15]。因此可忽略等式(2)的右端项,其无因次化后的形式为
| $ \dfrac{{{\partial ^2}{m_{{\rm{fD}}}}}}{{\partial x_{\rm{D}}^{\rm{2}}}} - \dfrac{\pi }{{{F_{\rm{D}}}}}{q_{{\rm{fD}}}} = 0 $ | (3) |
基于图 2的裂缝微元,将等式(3)离散为
| $ {m_{{\rm{f D}}i - 1}} - 2{m_{{\rm{fD}}i}} + {m_{{\rm{fD}}i + 1}} = \Delta x_{\rm{D}}^2\dfrac{\pi }{{{F_{\rm{D}}}}}{q_{{\rm{fD}}i}} $ | (4) |
由于倾斜缝沿斜井筒对称,只以井筒一侧的裂缝和储层为研究对象即可。根据公式(4),将图 2中的裂缝右半长共
| $ \left[{\begin{array}{*{20}{c}} {-4{\rm{ }}4/3{\rm{ }}0}& \cdots &{0\;0}&0\\ {1-2{\rm{ }}1}& \cdots &{0\;0}&0\\ \vdots & \cdots & \vdots &{}\\ {0\;\;0\;\;0}& \ddots &{1\;-2}&1\\ {0\;\;0\;\;0}& \cdots &{0\;1}&{ - 1} \end{array}} \right] \cdot \left[{\begin{array}{*{20}{c}} {{m_{{\rm{fD1}}}}}\\ {{m_{{\rm{fD2}}}}}\\ \vdots \\ {{m_{{\rm{fD}}{N_{\rm{f}}}-1}}}\\ {{m_{{\rm{fD}}{N_{\rm{f}}}}}} \end{array}} \right] = \\ \Delta x_{\rm{D}}^2\frac{{\rm{\pi }}}{{{F_{\rm{D}}}}}\left[{\begin{array}{*{20}{c}} {{q_{{\rm{fD1}}}}}\\ {{q_{{\rm{fD2}}}}}\\ \vdots \\ {{q_{{\rm{fD}}{N_{\rm{f}}}-1}}}\\ {{q_{{\rm{fD}}{N_{\rm{f}}}}}} \end{array}} \right] - \left[{\begin{array}{*{20}{c}} {8{m_{{\rm{wD}}}}/3}\\ 0\\ \vdots \\ 0\\ 0 \end{array}} \right] $ | (5) |
记等式(5)左端系数矩阵为
单相气体在上下封闭,水平无界,各向异性储层中的不稳定流动方程为
| $ {\eta _{\rm{h}}}\left( {\dfrac{{{\partial ^2}m}}{{\partial {x^2}}} + \dfrac{{{\partial ^2}m}}{{\partial {y^2}}}} \right) + {\eta _{\rm{v}}}\dfrac{{{\partial ^2}m}}{{\partial {z^2}}} = \dfrac{{\partial m}}{{\partial t}} $ | (6) |
将裂缝看成倾斜板源,地层流体不断流入裂缝造成储层压力不断下降。由倾斜板源函数[9]和叠加原理可得,井以定产量生产时,压裂倾斜缝在气藏中任意一点产生的拟压力降为
| $ \begin{array}{*{20}{l}} {{m_{\rm{D}}}\left( {{x_{\rm{D}}}, {y_{\rm{D}}}, {z_{\rm{D}}}, {t_{\rm{D}}};{\theta _{{{\rm{w}}^\prime }}}, {z_{{\rm{fD}}}}, {h_{{\rm{fD}}}}, {h_{\rm{D}}}} \right) = }\\ {\sum\nolimits_{j = - {N_{\rm{f}}}}^{{N_{\rm{f}}}} {\frac{{\sqrt {{\rm{ \pi }}} }}{{4{h_{{\rm{fD}}}}}} \cdot } \int_0^{{t_{\rm{D}}}} {{q_{{\rm{fD}}}}\left( {{x_{{\rm{D}}j}}, \tau } \right)\frac{1}{{\sqrt {{t_{\rm{D}}} - \tau } }}} \left( {{\rm{erf}}\frac{{1{\rm{ /}}2 + {x_{\rm{D}}} - {x_{{\rm{D}}j}}}}{{2{N_{\rm{f}}}\sqrt {{t_{\rm{D}}} - \tau } }} + {\rm{erf}}\frac{{1/2 - {x_{\rm{D}}} + {x_{{\rm{D}}j}}}}{{2{N_{\rm{f}}}\sqrt {{t_{\rm{D}}} - \tau } }}} \right) \times }\\ {\int_{ - \frac{{{h_{{\rm{fD}}}}}}{2}}^{\frac{{{h_{{\rm{fD}}}}}}{2}} {{\rm{exp}}\left[{-\frac{{{{\left( {{y_{\rm{D}}} + z\sin {\theta _{{{\rm{w}}^\prime }}}} \right)}^2}}}{{4\left( {{t_{\rm{D}}}-\tau } \right)}}} \right] \cdot } \\ \left[{1 + 2\sum\nolimits_{n = 1}^\infty {{\rm{exp}}\left( {-\frac{{{n^2}{\rm{ }}{{\rm{\pi }}^2}\tau }}{{h_{\rm{D}}^2}}} \right) \cdot } {\rm{cos}}\frac{{n{\rm{ \pi }}{z_{\rm{D}}}}}{{{h_{\rm{D}}}}} \cdot {\rm{cos}}\left( {n{\rm{ \pi }}\frac{{z\cos {\theta _{{{\rm{w}}^\prime }}}-{z_{{\rm{fD}}}}}}{{{h_{\rm{D}}}}}} \right)} \right]{\rm{d}}z{\rm{d}}\tau } \end{array} $ | (7) |
为求得井底压力动态,将连续时间离散。由气藏拟压力计算等式(7),可得第n时间点,第i裂缝微元的拟压力为
| $ \begin{array}{*{20}{l}} {m_{{\rm{fD}}i}^n\left( {{x_{{\rm{D}}i}}, 0, {z_{{\rm{fD}}}}, t_{\rm{D}}^n} \right) = }\\ {\sum\nolimits_{j = - {N_{\rm{f}}}}^{{N_{\rm{f}}}} {\sum\nolimits_{k = 1}^n {q_{{\rm{fD}}j}^k} } \int_{t_{\rm{D}}^{k - 1}}^{t_{\rm{D}}^k} {\frac{{\sqrt {{\rm{ \pi }}} }}{{4{h_{{\rm{fD}}}}}} \cdot \frac{1}{{\sqrt {t_{\rm{D}}^n - \tau } }}} \left( {{\rm{erf}}\frac{{1/2 + {x_{{\rm{D}}i}} - {x_{{\rm{D}}j}}}}{{2{N_{\rm{f}}}\sqrt {t_{\rm{D}}^n - \tau } }} + {\rm{erf}}\frac{{1/2 - {x_{{\rm{D}}i}} + {x_{{\rm{D}}j}}}}{{2{N_{\rm{f}}}\sqrt {t_{\rm{D}}^n - \tau } }}} \right) \times }\\ {\int_{ - \frac{{{h_{{\rm{fD}}}}}}{2}}^{\frac{{{h_{{\rm{fD}}}}}}{2}} {\exp \left[{-\frac{{{{\left( {z\sin {\theta _{{{\rm{w}}^\prime }}}} \right)}^2}}}{{4\left( {t_{\rm{D}}^n-\tau } \right)}}} \right] \cdot } \\ \left[{1 + 2\sum\nolimits_{n = 1}^\infty {\exp \left( {-\frac{{{n^2}{\rm{ }}{{\rm{\pi }}^2}\tau }}{{h_{\rm{D}}^2}}} \right) \cdot } \cos \frac{{n{\rm{ \pi }}{z_{{\rm{fD}}}}}}{{{h_{\rm{D}}}}} \cdot \cos \left( {n{\rm{ \pi }}\frac{{z\cos {\theta _{{{\rm{w}}^\prime }}}-{z_{{\rm{fD}}}}}}{{{h_{\rm{D}}}}}} \right)} \right]{\rm{d}}z{\rm{d}}\tau } \end{array} $ | (8) |
设等式(8)右端积分项为
| $ m_{{\rm{fD}}i}^n\left( {{x_{{\rm{D}}i}}, 0, {z_{{\rm{fD}}}}, t_{\rm{D}}^n} \right) = \sum\nolimits_{J = 1}^{{N_{\rm{f}}}} {\sum\nolimits_{k = 1}^n {q_{{\rm{fD}}J}^k \cdot GC_{i, J}^{n, k}} } $ | (9) |
对于离散的裂缝半长,等式(9)共有
| $ \left[{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {GC_{1, 1}^{n, n}} & \cdots \\ \end{array}} & {GC_{1, i}^{n, n}} & \cdots & {GC_{1, {N_{\rm{f}}}}^{n, n}} \\ {\begin{array}{*{20}{c}} \vdots & {} \\ \end{array}} & \vdots & {} & \vdots \\ {\begin{array}{*{20}{c}} {GC_{i, 1}^{n, n}} & \cdots \\ \end{array}} & {GC_{i, i}^{n, n}} & \cdots & {GC_{i, {N_{\rm{f}}}}^{n, n}} \\ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} \vdots \\ {GC_{{N_{\rm{f}}}, 1}^{n, n}} \\ \end{array}} & {\begin{array}{*{20}{c}} {} \\ \cdots \\ \end{array}} \\ \end{array}} & {\begin{array}{*{20}{c}} \vdots \\ {GC_{{N_{\rm{f}}}, i}^{n, n}} \\ \end{array}} & {\begin{array}{*{20}{c}} {} \\ \cdots \\ \end{array}} & {\begin{array}{*{20}{c}} \vdots \\ {GC_{{N_{\rm{f}}}, {N_{\rm{f}}}}^{n, n}} \\ \end{array}} \\ \end{array}} \right] \cdot \left[{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {q_{{\rm{fD1}}}^n} \\ \vdots \\ \end{array}} \\ {q_{{\rm{fD}}i}^n} \\ \vdots \\ {q_{{\rm{fD}}{N_{\rm{f}}}}^n} \\ \end{array}} \right] =\\ \left[{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {m_{{\rm{fD}}1}^n} \\ \vdots \\ \end{array}} \\ {m_{{\rm{fD}}i}^n} \\ \vdots \\ {m_{{\rm{fD}}{N_{\rm f}}}^n} \\ \end{array}} \right] - \left[{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\sum\nolimits_{J = 1}^{{N_{\rm{f}}}} {\sum\nolimits_{k = 1}^{n-1} {q_{{\rm{fD}}J}^k \cdot GC_{1, J}^{n, k}} } } \\ \vdots \\ \end{array}} \\ {\sum\nolimits_{J = 1}^{{N_{\rm{f}}}} {\sum\nolimits_{k = 1}^{n-1} {q_{{\rm{fD}}J}^k \cdot GC_{i, J}^{n, k}} } } \\ \vdots \\ {\sum\nolimits_{J = 1}^{{N_{\rm{f}}}} {\sum\nolimits_{k = 1}^{n-1} {q_{{\rm{fD}}J}^k \cdot GC_{{N_{\rm{f}}}, J}^{n, k}} } } \\ \end{array}} \right] $ | (10) |
记等式(10)左端系数矩阵为
考虑井筒存储效应的边界条件为
| $ 1 - \dfrac{{{C_{\rm{D}}}}}{{\Delta t_{\rm{D}}^n}}(m_{{\rm{wD}}}^n - m_{{\rm{wD}}}^{n - 1}) = \dfrac{1}{{{N_{\rm{f}}}}}\sum\nolimits_{i = 1}^{{N_{\rm{f}}}} {q_{{\rm{fD}}i}^n} $ | (11) |
等式(5)、式(10)和式(11)即是求解裂缝流量
| $ \left[{\begin{array}{*{20}{c}} {{N_{\rm{f}}}{C_{\rm{D}}}/\Delta t_{\rm{D}}^n}&{{\boldsymbol{O}^{\rm{T}}}}&{{\boldsymbol{D}^{\rm{T}}}}\\ \boldsymbol{C}&\boldsymbol{A}&{-\boldsymbol{I}}\\ \boldsymbol{O}&\boldsymbol{I}&\boldsymbol{B} \end{array}} \right] \cdot \left[{\begin{array}{*{20}{c}} {m_{{\rm{wD}}}^n}\\ {\boldsymbol{m}_{{\rm{fD}}}^n}\\ {\boldsymbol{q}_{{\rm{fD}}}^n} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {{N_{\rm{f}}} + {N_{\rm{f}}}{C_{\rm{D}}}m_{{\rm{wD}}}^{n-1}{\rm{ /}}\Delta t_{\rm{D}}^n}\\ \boldsymbol{O}\\ \boldsymbol{b} \end{array}} \right] $ | (12) |
其中:
D——
I——
O——
将等式(12)编程实现,再对离散时间段和裂缝微元数进行敏感性分析。大量计算表明,等分裂缝半长为10个微元,并将时间在一个对数区间内分为1、2、5、8时间点可以得到精确的计算结果。
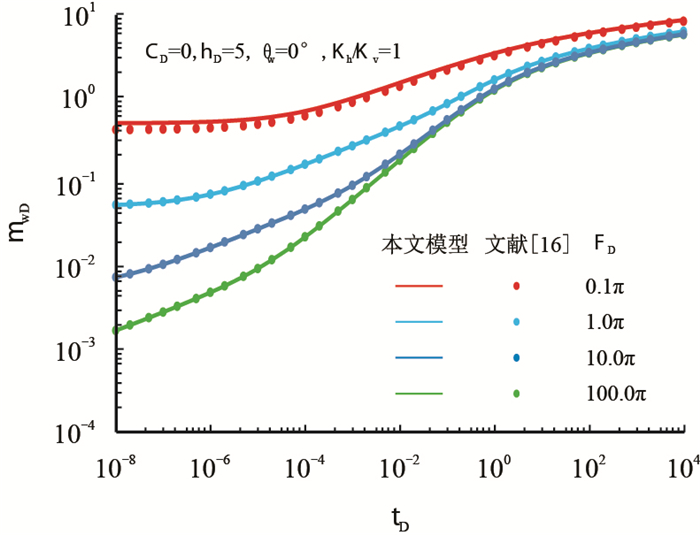
为验证模型的准确性,分别利用有限导流垂直缝和无限导流倾斜缝两个特例验证。对于垂直缝有限导流,与Cinco L H结果[16]对比。如图 3所示,在低裂缝导流能力(
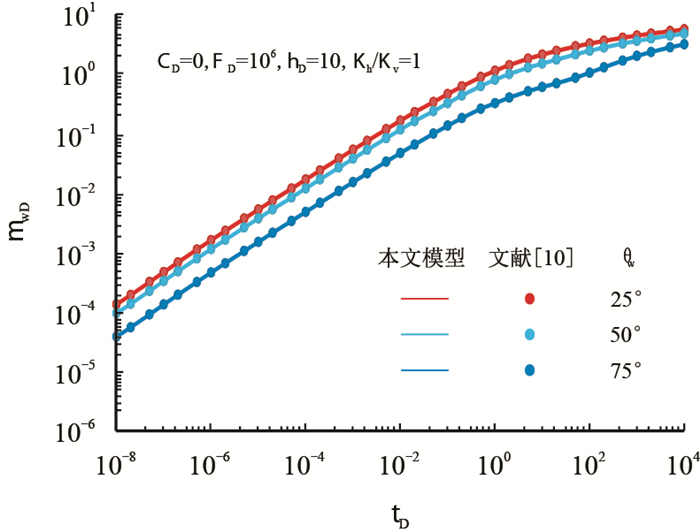
对倾斜裂缝无限导流,与Dinh A V模型[10]对比。如图 4所示,在整个生产时间内,本文结果与文献[16]结果一致。由此说明,本文建立的压裂倾斜缝流动模型计算结果可靠。
3.2 压力动态特征假设斜井筒在生产段压裂后,形成图 1所示的倾斜缝。各无因次参数取值为:裂缝导流能力
如图 5所示,不考虑井筒储存效应时,压裂倾斜缝流动形态可划分为:(1)裂缝与地层双线性流;(2)地层线性流;(3)早期径向流;(4)拟复合线性流;(5)晚期拟径向流。
 |
| 图5 不考虑井筒存储效应的倾斜缝压力及压力导数曲线 Fig. 5 Pressure and derivative responses of inclined fracture without the effect of wellbore storage |
(1) 裂缝与地层双线性流是由倾斜缝内稳定线性流和气藏不稳定线性流组成(图 6a)。在该阶段,流动只发生于裂缝及附近地层,压力波未达到上下封闭边界。在双对数图上,压力及压力导数都呈现斜率为1/4的直线段。Cinco-Ley[17]给出了压裂直缝双线性流的井底压力解析表达式
| $ {p_{{\rm{wD}}}} = \frac{{2.45}}{{\sqrt {{F_{\rm{D}}}} }}t_{\rm{D}}^{1{\rm{ /}}4} $ | (13) |
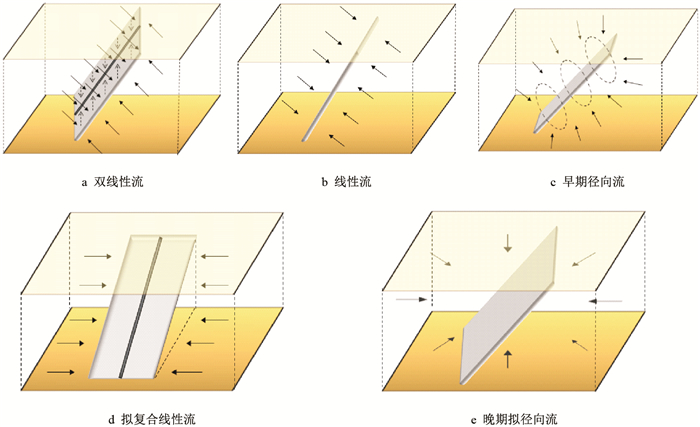 |
| 图6 倾斜缝各流动阶段示意图 Fig. 6 Schematic of flow regimes of inclined fracture |
将公式(13)引入到倾斜缝,则有
| $ \frac{{{K_{\rm{h}}}{h_{\rm{f}}}\left[{m({p_{\rm{i}}})-m({p_{\rm{w}}})} \right]}}{{1.291 \times {{10}^{ -3}}{q_{\rm{w}}}T}} = \frac{{2.45}}{{\sqrt {{F_{\rm{D}}}} }}t_{\rm{D}}^{1{\rm{ /}}4} $ | (14) |
由于裂缝贯穿储层,有
| $ \frac{{{K_{\rm{h}}}h\left[{m({p_{\rm{i}}})-m({p_{\rm{w}}})} \right]}}{{1.291 \times {{10}^{ -3}}{q_{\rm{w}}}T \cdot \cos {\theta _{\rm{w}}}}} = \frac{{2.45}}{{\sqrt {{F_{\rm{D}}}} }}t_{\rm{D}}^{1{\rm{ /}}4} $ | (15) |
结合无因次井底压力定义,并考虑储层渗透率各向异性,可得压裂倾斜缝在双线性流阶段的井底压力解析表达式为
| $ \begin{array}{l} {m_{{\rm{wD}}}} = \frac{{{K_{\rm{h}}}h\sqrt {{K_{\rm{h}}}/{K_{\rm{v}}}} \left[{m({p_{\rm{i}}})-m({p_{\rm{w}}})} \right]}}{{1.291 \times {{10}^{ -3}}{q_{\rm{w}}}T}} = \\ \;\;\;\;\;\cos {\theta _{{{\rm{w}}^\prime }}}\frac{{2.45}}{{\sqrt {{F_{\rm{D}}}} }}t_D^{1/4} \end{array} $ | (16) |
(2) 地层线性流是指流动初期地层流体线性地垂直于裂缝面流向倾斜缝(图 6b)。此时,压力波仍未达到上下封闭边界。压力及压力导数在双对数曲线上表现为斜率1/2的直线。由Gringarten[18]给出的压裂直缝线性流井底压力解析表达式
| $ {p_{\rm{wD}}} = \sqrt {\pi {t_{\rm{D}}}} $ | (17) |
可以推得压裂倾斜缝在地层线性流阶段的井底压力解析表达式为
| $ {m_{\rm{wD}}} = \dfrac{{{K_{\rm{h}}}h\sqrt {{K_{\rm{h}}}/{K_{\rm{v}}}} \left[{m({p_{\rm{i}}})-m({p_{\rm{w}}})} \right]}}{{1.291 \times {{10}^{ - 3}}{q_{\rm{w}}}T}} = \\ \cos \theta_{\rm{w}}'\sqrt {\pi {t_{\rm{D}}}} $ | (18) |
(3) 早期径向流是指若气藏厚度大,压裂缝横向延伸短,且井斜角较大时,倾斜缝几何形态类似于斜井,则在裂缝周围产生倾斜径向流动(图 6c)。反之,该流动阶段不会出现。压力导数在双对数诊断图上表现为一水平线,其值为
| $ {t_{\rm{D}}} \cdot {m_{\rm{wD}}'} = 0.5\cos\theta_{\rm{w}}' $ | (19) |
(4) 由图 6d可以看出,拟复合线性流出现于早期径向流之后,其产生的条件与早期径向流相同。该阶段的流动特征与多段压裂水平井的复合线性流相似,压力导数在双对数图上呈斜率为1/2的直线。
(5) 晚期拟径向流是指在水平无界气藏中,地层流体以拟径向流的形式向压裂缝流动,压力波以圆形等值线向外传播(图 6e)。在双对数诊断图上无因次压力导数表现为大小0.5的水平直线段。
图 7为考虑井筒存储效应的倾斜缝压力及压力导数曲线,由图可以看出,考虑井筒存储效应时,井筒续流段(图 7中的(1)区)掩盖了裂缝与地层双线性流阶段,其他流动阶段均与图 5所示的(2)、(3)、(4)、(5)相同。如果井筒存储系数更大,续流段甚至还会掩盖地层线性流阶段。
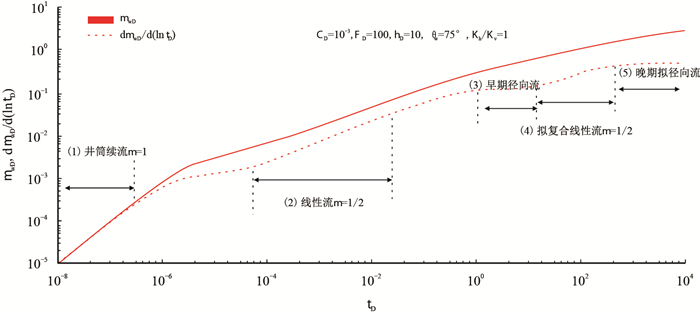 |
| 图7 考虑井筒存储效应的倾斜缝压力及压力导数曲线 Fig. 7 Pressure and derivative responses of inclined fracture with the effect of wellbore storage |
影响倾斜缝压力动态的因素有裂缝倾斜角、无因次裂缝导流能力、气藏厚度和储层渗透率各向异性。
从图 8所示倾斜角对压裂倾斜缝压力动态影响的双对数曲线中可以看出,裂缝倾斜角对压力动态影响较大,几乎贯穿了整个生产时间段,直到流动达到拟径向流阶段。裂缝倾角越大,无因次井底压力及压力导数就越小,且随倾角的增大,减小幅度变大。这是由于随着倾斜角增大,裂缝与储层的接触面积变大,近井渗流阻力减小,而当倾斜角大于60℃时,其余弦值急剧减小,使得压力值减幅增大。同时可以得出,裂缝倾斜角较小时(
 |
| 图8 倾斜角对压裂倾斜缝压力动态的影响 Fig. 8 The effect of inclination angle on transient responses of inclined fracture |
图 9给出了不同裂缝导流能力下的倾斜缝压力响应双对数曲线,可以看出裂缝导流能力对压力动态的影响主要在生产的早中期,即双线性流及线性流阶段。无因次裂缝导流较小时(
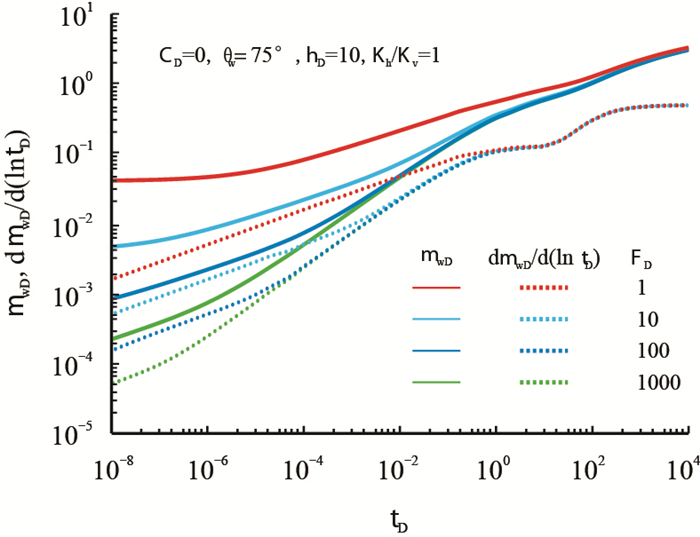 |
| 图9 裂缝导流能力对压裂倾斜缝压力动态的影响 Fig. 9 The effect of fracture conductivity on transient responses of inclined fracture |
图 10为气藏厚度对压裂倾斜缝压力动态影响,从压力动态双对数曲线上可以得出,气藏厚度只影响早期径向流和拟复合线性流。无因次气藏厚度较小时(
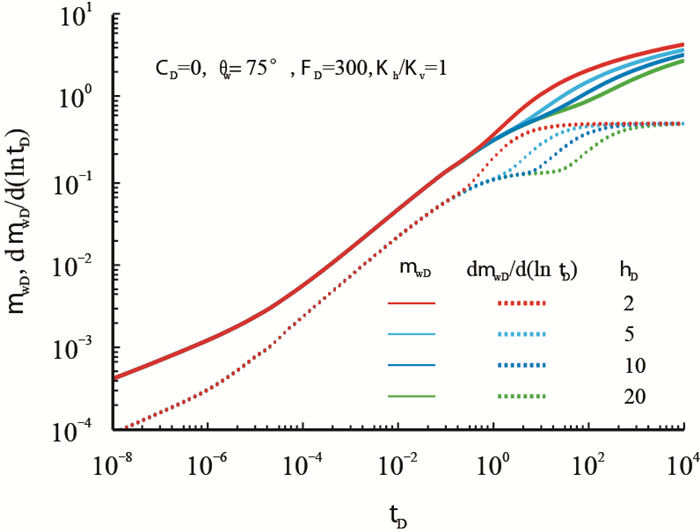 |
| 图10 气藏厚度对压裂倾斜缝压力动态的影响 Fig. 10 The effect of formation thickness on transient responses of inclined fracture |
储层渗透率各向异性对压裂倾斜缝压力动态的影响见图 11,可以看出,渗透率各向异性影响了除拟径向流外的生产时间段。随渗透率各向异性的增强,拟复合线性流持续时间减少,早期径向流阶段的无因次压力导数值变大,最终与晚期拟径向流合并而消失。这是由于当
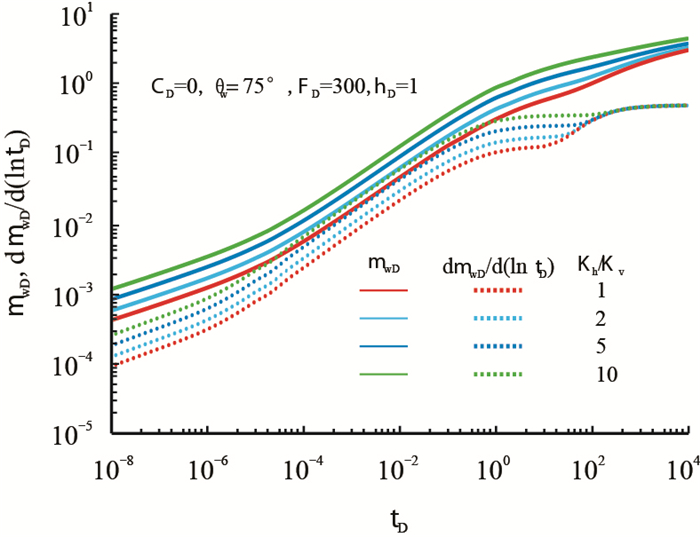 |
| 图11 储层渗透率各向异性对压裂倾斜缝压力动态的影响 Fig. 11 The effect of permeability anisotropy on transient responses of inclined fracture |
基于以上的研究理论,以苏里格气田一口压裂定向井为例,利用本文流动模型解释该井的压力测试结果,为矿场同类井的压裂设计及压后效果评价提供实例基础。解释所需的参数为:气藏有效厚度37 m,平均孔隙度0.19,储层水垂渗透率比为5,井筒半径0.09 m,综合压缩系数13.83
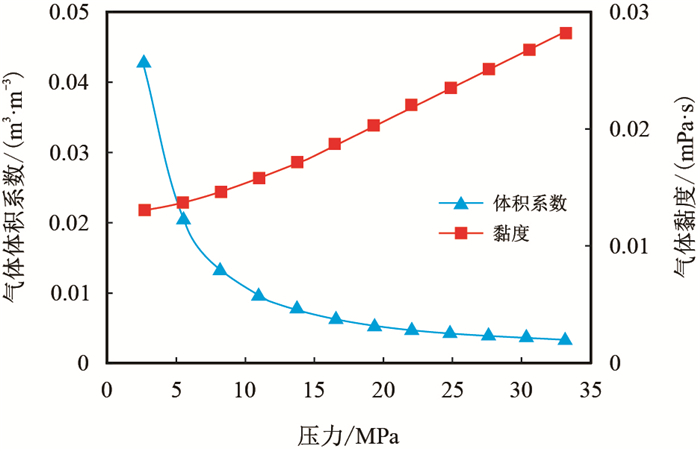 |
| 图12 气体PVT高压物性 Fig. 12 Pressure/volume/temperature property of gas |
利用遗传算法[19, 20],拟合理论值与实际测试数据,优化储层渗透率、裂缝倾斜角、裂缝半长和导流能力。由图 13所示的压力恢复双对数拟合结果可得解释参数如下:储层渗透率
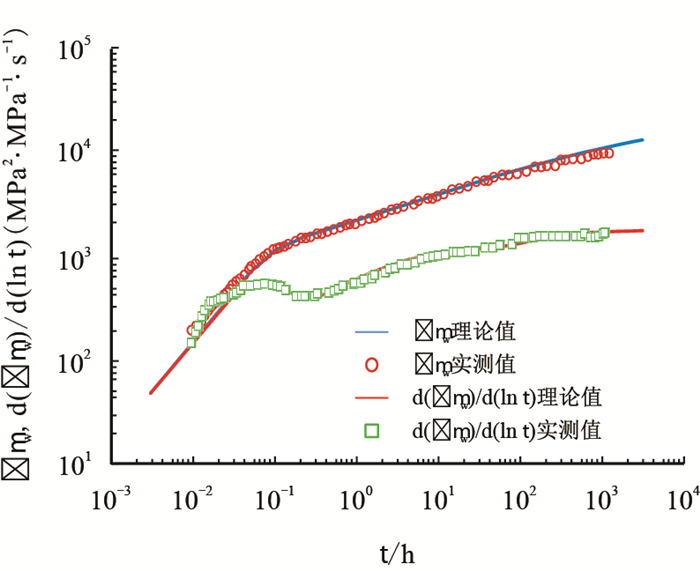 |
| 图13 理论值与实测数据拟合效果图 Fig. 13 Matching of the field data with the theoretical value |
(1) 针对压裂倾斜缝,通过离散裂缝为微元,利用实空间倾斜板源函数及势叠加原理,建立了压裂倾斜缝不稳定流动模型。
(2) 明确了倾斜缝的流动特征,并给出了对应流动阶段的井底压力解析表达式。不考虑井筒储存效应时,压裂倾斜缝流动形态分为:裂缝与地层双线性流、地层线性流、早期径向流、拟复合线性流和晚期拟径向流。其中早期径向流和拟复合线性流只有在气藏厚度大,压裂缝短,且井斜角较大时才会出现。当考虑井筒存储效应时,井筒续流段会掩盖裂缝与地层双线性流。
(3) 参数敏感性分析表明:裂缝倾斜角和储层渗透率各向异性对井底压力动态影响时间最长,会一直延续到晚期拟径向流阶段。无因次裂缝导流能力唯一决定了裂缝与地层双线性流和地层线性流的出现与否及持续时间。随着储层厚度的增大,早期径向流的持续时间增加,拟复合线性流的出现时间推迟。
(4) 现场实例验证了本文模型的正确性。
符号说明
m——气体拟压力,MPa2/(mPa
p——地层压力,MPa;
Z——气体压缩因子,无因次;
h——储层厚度,m;
T——地层温度,℃;
t——时间,h;
n——离散生产时间点,无因次;
下标w——生产井;
下标f——裂缝;
下标i——裂缝微元索引;
下标D——无因次。
| [1] |
刁素, 颜晋川, 任山, 等. 川西地区定向井压裂工艺技术研究及应用[J].
西南石油大学学报:自然科学版, 2009, 31 (1) : 111 –115.
Diao Su, Yan Jinchuan, Ren Shan, et al. Research and field application on hydraulic fracturing technology of directional wells in western region of Sichuan[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2009, 31 (1) : 111 –115. |
| [2] |
贾长贵, 李明志, 李凤霞, 等. 低渗裂缝型气藏斜井压裂技术研究[J].
天然气工业, 2007, 27 (5) : 106 –108.
Jia Changgui, Li Mingzhi, Li Fengxia, et al. A study on fracturing technology of deviated wells in lowpermeability, fractured gas reservoir[J]. Natural Gas Industry, 2007, 27 (5) : 106 –108. |
| [3] | 牛增前, 隋向云, 张平. 大斜度井压裂工艺研究[J]. 石油钻采工艺, 2005, 27 (S) : 61 –63. |
| [4] | Daneshy A A. A study of inclined hydraulic fractures[J]. SPE Journal, 1973, 13 (2) : 61 –68. DOI:10.2118/4062-PA |
| [5] | Wright C A, Stewart D W, Emanuele M A. Reorientation of propped refracture treatments in the Lost Hills Field[C]. SPE 27896, 1994. |
| [6] |
陈勉, 陈治喜, 黄荣樽. 大斜度井水压裂缝起裂研究[J].
石油大学学报:自然科学版, 1995, 19 (2) : 30 –35.
Chen Mian, Chen Zhixi, Huang Rongzui. Hydraulic fracturing of highly deviated wells[J]. Journal of the University of Petroleum, China, 1995, 19 (2) : 30 –35. |
| [7] |
张广清, 陈勉, 王强. 斜井井筒附近水力裂缝空间转向模型研究[J].
石油大学学报:自然科学版, 2004, 28 (4) : 51 –55.
Zhang Guangqing, Chen Mian, Wang Qiang. Threedimensional model for space reorientation of hydraulic fractures near deflecting well bore[J]. Journal of the University of Petroleum, China, 2004, 28 (4) : 51 –55. |
| [8] |
贾长贵, 李明志, 邓金根, 等. 斜井压裂大型真三轴模拟试验研究[J].
西南石油大学学报, 2007, 29 (2) : 135 –137.
Jia Changgui, Li Mingzhi, Deng Jingen, et al. Large-scale three dimensional simulation test for directional perforation and fracturing in deflected well[J]. Journal of Southwest Petroleum University, 2007, 29 (2) : 135 –137. |
| [9] | Cinco L H, Miller F G, Ramey H J. Unsteady-state pressure distribution created by a directionally drilled well[C]. SPE 5591, 1975. |
| [10] | Dinh A V, Tiab D. Transient-pressure analysis of a well with an inclined hydraulic fracture using type curve matching[C]. SPE 120545, 2009. |
| [11] |
马时刚, 苏彦春, 王世民, 等. 拟压力不同简化形式对气井产能计算的影响[J].
天然气勘探与开发, 2010, 33 (3) : 30 –32.
Ma Shigang, Su Yanchun, Wang Shimin, et al. Effects of pseudo pressure in differently simplified forms on productivity calculation[J]. Natural Gas Exploration & Development, 2010, 33 (3) : 30 –32. |
| [12] | 张枫, 赵仕民, 秦建敏, 等. 有限导流裂缝水平井产能研究[J]. 天然气地球科学, 2009, 20 (5) : 817 –821. |
| [13] |
王军磊, 贾爱林, 何东博, 等. 致密气藏分段压裂水平井产量递减规律及影响因素[J].
天然气地球科学, 2014, 25 (2) : 278 –285.
Wang Junlei, Jia Ailin, He Dongbo, et al. Rate decline of multiple fractured horizontal well and influence factors on productivity in tight gas reservoirs[J]. Natural Gas Geoscience, 2014, 25 (2) : 278 –285. |
| [14] |
魏漪, 宋新民, 冉启全, 等. 致密油藏压裂水平井非稳态产能预测模型[J].
新疆石油地质, 2014, 35 (1) : 67 –72.
Wei Yi, Song Xinmin, Ran Qiquan, et al. An unstable productivity prediction model for fractured horizontal well in tight oil reservoirs[J]. Xinjiang Petroleum Geology, 2014, 35 (1) : 67 –72. |
| [15] |
焦春艳, 何顺利, 张海杰, 等. 变导流能力下压裂井生产动态研究[J].
西南石油大学学报:自然科学版, 2011, 33 (4) : 107 –110.
Jiao Chunyan, He Shunlin, Zhang Haijie, et al. Study on production performance of fractured well under the condition of variable conductivity[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2011, 33 (4) : 107 –110. |
| [16] | Cinco L H, Samaniego V F, Dominguez A N. Transient pressure behavior for a well with a finite-conductivity vertical fracture[C]. SPE 6014, 1978. |
| [17] | Cinco L H, Samaniego V F. Transient pressure analysis for fractured wells[J]. Journal of Petroleum Technology, 1981, 33 (9) : 1749 –1766. DOI:10.2118/7490-PA |
| [18] | Gringarten A C, Ramey H J. The use of source and greens functions in solving unsteady-flow problems in reservoirs[J]. SPE Journal, 1973, 13 (5) : 285 –296. DOI:10.2118/3818-PA |
| [19] |
黄辉, 吴晓东, 孙天礼. 基于遗传算法的低渗透气藏水平井压裂参数优化[J].
天然气工业, 2008, 28 (5) : 91 –93.
Huang Hui, Wu Xiaodong, Sun Tianli. Genetic algorithmbased optimizing hydraulic fracturing parameters for horizontal wells in low-permeability reservoirs[J]. Natural Gas Industry, 2008, 28 (5) : 91 –93. |
| [20] |
吴明录, 姚军, 王子胜, 等. 利用双种群遗传算法进行数值试井自动拟合[J].
油气地质与采收率, 2007, 14 (2) : 81 –83.
Wu Minglu, Yao Jun, Wang Zisheng, et al. Numerical well testing auto-matching applying double population genetic algorithm[J]. Petroleum Geology and Recovery Efficiency, 2007, 14 (2) : 81 –83. |
 2015, Vol. 37
2015, Vol. 37