2. 中国石化东北石油局, 吉林 长春 130062
2. Northeast Petroleum Bureau, SINOPEC, Changchun, Jilin 130062, China
页岩气储层纳米孔隙特征体现了与其他气藏不同的地质特征和渗流特征[1-4],页岩气储层基质孔喉直径约为1~1 000 nm,渗透率
针对页岩气储层扩散作用机理,国内外学者做了较多研究[5-9]。2002年,Civan指出,气体在微孔介质中的流动状态取决于介质本身的岩石物理性质和气体分子平均自由程[10, 11],并归纳总结了Liepman,Stahl和Kaviany等人研究成果,提出利用克努森数划分气体流动区域;2007年阿尔伯特研究中心的Javadpour F等[12]首次提出了页岩气藏纳米级孔隙中的流动不能简单地以渗流处理,并对页岩气藏中气体的平均自由程和克努森数进行了测试分析;Thorstenson D C等[13]开展了关于Fick定律描述多孔介质中的气体扩散的应用研究;田冷等[14]考虑页岩气解吸、扩散、渗流,建立了页岩气多级压裂水平井产能模型。
基于以上成果,结合考虑解吸{\twodash}吸附的页岩气藏压裂水平井的三线性渗流模型,建立了考虑扩散作用的扩展模型,并进行了解析解的推导,从而定量分析扩散作用对页岩气藏生产的影响程度。
1 页岩气渗流扩散作用界限随着压力梯度的增加,大量的气体从基岩有机质表面解吸出来而进入纳米孔隙中,极低的渗透率较难形成达西渗流,而以页岩气分子由高浓度区向低浓度区的扩散过程为其主要渗流模式,尤其是当孔隙直径很小和压力较低时,扩散作用更为明显。
从分子运动论的观点来看,气体扩散的本质是气体分子不规则热运动的结果,根据气体在多孔介质中的扩散机理的研究[15-18],可以用克努森(Knudsen)数评价扩散作用的大小,克努森数(
| $ {K_{\rm{n}}} = \dfrac{\lambda }{d} $ | (1) |
| $ \lambda = \dfrac{k_{\rm{B}}T}{{\sqrt 2 \pi {\delta ^2}p}} \times {10^{21}} $ | (2) |
若保持压力不变,孔隙直径变大时,
以页岩气中的主要成分甲烷分子为例,计算不同压力下气体分子的自由程(其中:
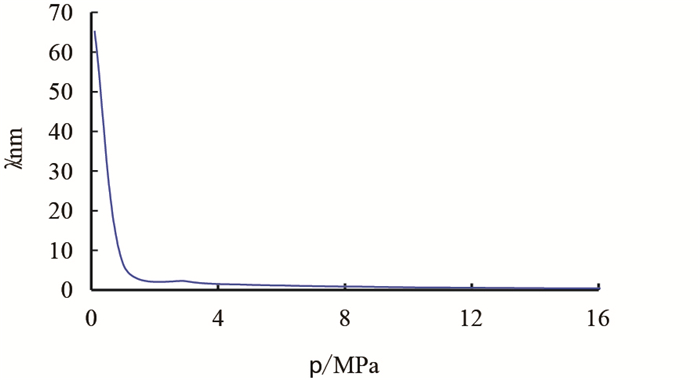 |
| 图1 分子自由程与压力的关系图 Fig. 1 Relationship between molecular free path and pressure |
在常温常压下(20℃,0.10 MPa),甲烷分子的平均自由程约为63.00 nm。在实际页岩气储层中,甲烷分子的压力远大于常压,所以,实际气藏条件下甲烷分子的平均自由程要小的多(图 1),整体表现为
气藏温度一定(
 |
|
图2
不同孔隙直径下克努森系数与压力的关系图
Fig. 2
Relationship between |
由图 2可以看出,由直径小于100.00 nm的孔隙构成的页岩气储层,实际生产中,井底压力一般都会低于10.00~MPa,甚至可达到5.00~MPa,因此,其基质的渗流过程会受扩散作用的影响,且孔隙半径越小,随着井底压力的下降,扩散作用越显著。
2 考虑扩散作用的页岩气藏渗流模型 2.1 考虑扩散作用的流动方程2007年,Florence F A等[19, 20]通过引入克努森系数,提出了适合致密气和页岩气非达西扩散流动渗透率表达式,该表达式把微观渗流转换为了宏观渗流的形式
| $ K = {K_0}\left [\dfrac{{128}}{{15{\pi ^2}}}{\tan ^{-1}}(4{K_{\rm{n}}}^{0.4}){K_{\rm{n}}}\right]\left [1 + \dfrac{{4{K_{\rm{n}}}}}{{1 + {K_{\rm{n}}}}}\right] $ | (3) |
由于页岩气在储层中的流动一般都在高压下进行(大于5.00 MPa),分子自由程随压力变化已经很小,因此,克努森系数可认为是一个常数,其运动方程可写为
| $ v = - \dfrac{K}{\mu }\dfrac{{{\rm{d}}p}}{{{\rm{d}}x}} = \\ \,\,\,\,- \dfrac{{{K_0}\left [\dfrac{{128}}{{15{\pi ^2}}}{{\tan }^{-1}}(4{K_{\rm{n}}}^{0.4}){K_{\rm{n}}}\right]\left [1 + \dfrac{{4{K_{\rm{n}}}}}{{1 + {K_{\rm{n}}}}}\right]}}{\mu }\dfrac{{{\rm{d}}p}}{{{\rm{d}}x}} $ | (4) |
运用该方程可建立考虑扩散作用的页岩气藏压裂水平井三线性渗流模型。
2.2 三线性渗流模型页岩气藏水平井压裂会形成带有一条主裂缝的裂缝网络,页岩气则通过基岩解吸、扩散和渗流到达裂缝网络中,然后,通过主裂缝流入井内,形成了完整的渗流过程。然而,基岩、裂缝网络和主裂缝的渗流有比较明显的区别。基岩是页岩气的存储空间,其渗流多级模式突出;裂缝网络增加渗流通道,形成基岩与主裂缝的连通桥梁,同时,也有部分游离气参与渗流;主裂缝是主要渗流通道,是井与储层之间的接触桥梁,渗透率很高。以上3种介质中的渗流很复杂,按其关系进行简化。即分成如图 3中的3个部分渗流模式,由于天然气在3个部分的渗流速度较为缓慢,因此,假设3个部分都遵循线性渗流,即定义为三线性渗流。
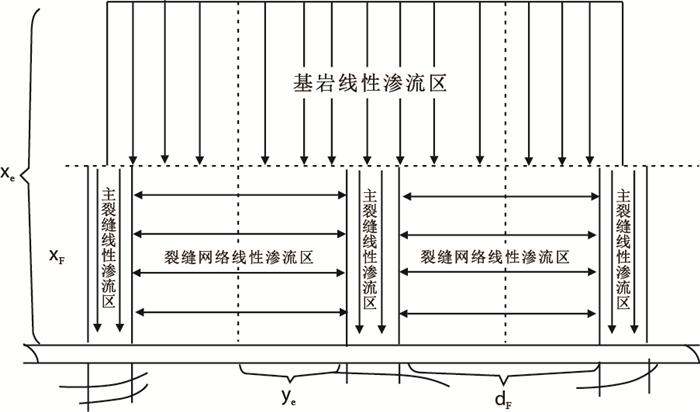 |
| 图3 多级压裂水平井三线性渗流模型示意图 Fig. 3 The model of three-linear seepage in multi-stage fractured horizontal well |
(1) 基岩渗流:基岩中页岩气通过裂缝面渗入裂缝网络,简化为通过基岩整体以线性渗流模式流入裂缝网络系统,其几何规模为平面上的压裂网络区域的3/4;
(2) 裂缝网络渗流:把页岩气在裂缝网络体系中的渗流简化为由两主裂缝中间分别向各自主裂缝的线性渗流,渗流通道是裂缝网络等效渗透率,其值可等价为天然裂缝渗透率,一般为基质渗透率的100倍;
(3) 主裂缝渗流:将主裂缝内的渗流简化为接受两边裂缝网络窜流的主裂缝空间的线性渗流,其渗透率可达到几百,甚至几千毫达西。
根据建立的模型及压裂缝网的分布,定义图 3中的参数:
则3个部分的渗流数学模型为:
基质渗流方程
| $ - \dfrac{\partial }{{\partial x}}\left[{{\rho _{{\rm{gm}}}}{v_{\rm{m}}}} \right] = \dfrac{\partial }{{\partial t}}\left( {{\phi _{\rm{m}}}{\rho _{{\rm{gm}}}} + {\rho _{{\rm{gsc}}}}{V_{\rm{E}}}} \right) $ | (5) |
裂缝网络渗流方程
| $ - \dfrac{\partial }{{\partial y}}\left[{{\rho _{{\rm{gf}}}}{v_f}} \right] + 2{q_{{\rm{mf}}}} = \dfrac{\partial }{{\partial t}}\left( {{\phi _{\rm{f}}}{\rho _{{\rm{gf}}}}} \right) $ | (6) |
主裂缝渗流方程
| $ - \dfrac{\partial }{{\partial x}}\left[{{\rho _{{\rm{gF}}}}{v_{\rm{F}}}} \right] + 2{q_{{\rm{fF}}}} = \dfrac{\partial }{{\partial t}}\left( {{\phi _{\rm{F}}}{\rho _{{\rm{gF}}}}} \right) $ | (7) |
其中:
| ${v_{\rm{m}}} = - \dfrac{{{K_{\rm{m}}} \dfrac{{128}}{{15{\pi ^2}}}{{\tan }^{ - 1}}\left (4{K_{\rm{n}}}^{0.4}\right ){K_{\rm{n}}} \left (1 + \dfrac{{4{K_{\rm{n}}}}}{{1 + {K_{\rm{n}}}}}\right )}}{\mu }\dfrac{{{\rm{d}}p}}{{{\rm{d}}x}};$ |
| ${v_{\rm{f}}} = - \dfrac{{{K_{\rm{f}}}}}{\mu }\dfrac{{\partial {p_{\rm{f}}}}}{{\partial y}};$ |
| ${v_{\rm{F}}} = - \dfrac{{{K_{\rm{F}}}}}{\mu }\dfrac{{\partial {p_{\rm{F}}}}}{{\partial y}};$ |
| ${\rho _{\rm{gm}}} = \dfrac{{{p_{\rm{m}}}M}}{{RTz}};$ |
| ${\rho _{\rm{gf}}} = \dfrac{{{p_{\rm{f}}}M}}{{RTz}};$ |
| ${\rho _{\rm{gF}}} = \dfrac{{{p_{\rm{F}}}M}}{{RTz}};$ |
| ${V_{\rm{E}}} = \dfrac{{{V_{\rm{L}}}{p_{\rm{m}}}}}{{{p_{\rm{L}}} + {p_{\rm{m}}}}};$ |
| ${q_{\rm{mf}}} = {\rho _{\rm{gm}}}{q_{\rm{gf}}} = \dfrac{{{p_{\rm{m}}}}}{z}\dfrac{M}{{RT}}\dfrac{{{{\rm k}_{\rm{m}}}}}{\mu }\dfrac{{\partial {p_{\rm{m}}}}}{{\partial x}}\left| {_{x = {x_{\rm{F}}}}} \right.;$ |
| ${q_{\rm{fF}}} = {\rho _{\rm{gf}}}{q_{\rm{gf}}} = \dfrac{{{p_{\rm{f}}}}}{z}\dfrac{M}{{RT}}\dfrac{{{k_{\rm{f}}}}}{\mu }\dfrac{{\partial {p_{\rm{f}}}}}{{\partial x}}\left| {_{y = {y_{\rm{e}}}}} \right.。$ |
经过渗流方程的整理和拉普拉斯的变换,可得到单一主裂缝到井筒的流量公式
| $ \begin{split} {q_{\rm{F}}} = & \dfrac{{6.89 \times {{10}^6}\left( {p_{\rm i}^2 - p_{{\rm{wf}}}^2} \right){K_{\rm{f}}}h{C_{{\rm{FD}}}}{x_{\rm{e}}}{{\left\{ {{K_{\rm{m}}}\left[{\dfrac{{128}}{{15{p_{\rm i} ^2}}}{{\tan }^{-1}}\left( {4{K_{\rm{n}}}^{0.4}} \right){K_{\rm{n}}}} \right]\left[{1 + \dfrac{{4{K_{\rm{n}}}}}{{1 + {K_{\rm{n}}}}}} \right]} \right\}}^2}\left( {{y_{{\rm{eD}}}} - \dfrac{{{W_{\rm{D}}}}}{2}} \right)}}{{\pi {y_{{\rm{eD}}}}{\eta _{\rm{m}}}T\mu z}}\cdot\\[6pt] & \left[{2{\eta _{\rm{f}}}\left( {{x_{{\rm{eD}}}}-1} \right) + {C_{{\rm{fD}}}}{y_{{\rm{eD}}}}{\eta _{\rm{m}}} + {C_{{\rm{FD}}}}^2{y_{{\rm{eD}}}}{\eta _{\rm{m}}}} \right]t_{\rm{D}}^{ - 1/4} \end{split} $ | (8) |
其中:
| ${C_{\rm{FD}}} = {{K_{\rm{F}}}w}/{K_{\rm{f}}x_{\rm{F}}};$ |
| ${C_{\rm{Fd}}} = {K_{\rm{m}}x_{\rm{F}}}/{K_{\rm{m}}y_{\rm{e}}};$ |
| ${x_{\rm{eD}}} = {{{x_{\rm{e}}}}}/{{{x_{\rm{F}}}}};$ |
| ${y_{\rm{eD}}} = {{{y_{\rm{e}}}}}/{{{x_{\rm{F}}}}};$ |
| ${w_{\rm{D}}} = {w}/{{{x_{\rm{F}}}}};$ |
| ${t_{\rm{D}}} = 1.69 \times {10^{ - 7}}\dfrac{{{K_{\rm{f}}}}}{{{\phi _{\rm{f}}}\mu {C_{\rm{tf}}}{x_{\rm{F}}}^2}}t。$ |
则水平井总的流量
| $ q = {q_{\rm{F}}}{n_{\rm{F}}} $ | (9) |
由图 1可以看到,储层压力大于8.00 MPa时,分子自由程随着压力的增加而趋于一个定值(0.5 nm左右),因此,井底压力大于8.00 MPa时,扩散作用将与分子自由程无关,而只与孔隙直径有关。
将多孔介质抽象为一簇毛细管,假设孔隙度一定,应用Poiseuille公式得到不同孔隙直径对应的渗透率。
| $ d = 5.66 \times {10^3}\sqrt {\dfrac{K}{\phi }} $ | (10) |
假设2000 m深的气藏压力为20.00 MPa,基质孔隙度为0.045,则可计算不同孔隙直径受扩散作用引起的渗透率增大程度,结果如表 1。从表中可以看出,随着孔隙直径的增大,扩散作用引起的渗透率增大值在减小,尤其是孔隙小于10.00 nm时,渗透率的变化非常大,当孔隙达到35.70 nm时,扩散带来的渗透率增加趋于0,达到了扩散的适用阈值,亦即若孔隙直径小于35.70 nm时,渗流要考虑扩散作用,若大于35.70 nm时,扩散作用可以不用考虑。
| 表1 不同孔径下扩散作用的渗透率增加程度 Table 1 Value added of permeability by diffusion for different pore |
应用考虑扩散作用的模型解析解分析压裂水平井的产量变化,基础数据如表 2所示。
| 表2 气藏基本参数 Table 2 Basic parameter of the gas reservoir |
在扩散作用范围内,不同孔隙大小的页岩气储层所对应的气井产量增加值如图 4所示,初产时期,扩散作用所带来的产量增加值最大可达5 000 m
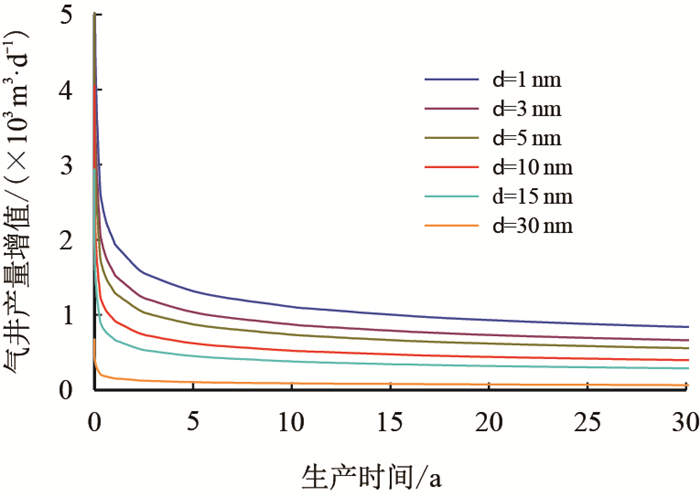 |
| 图4 不同孔隙直径下扩散对气井生产的影响 Fig. 4 The effect of diffusion for different pore |
若已知孔隙直径,以渗透率增加至趋于0为标准,计算扩散作用下的压力阈值为表 3所示,当生产时的压力低于此值时就需要考虑扩散作用。
| 表3 不同孔隙直径下扩散影响的压力阀值 Table 3 Limited value of pressure by diffusion for different pore |
当孔隙直径(
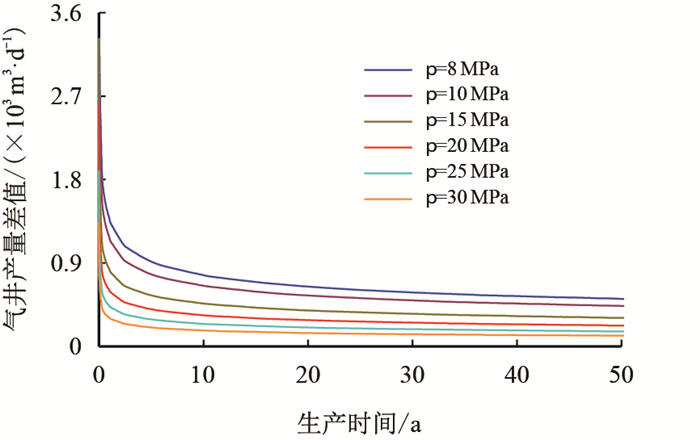 |
| 图5 不同储层压力下扩散对气井生产的影响 Fig. 5 The effect of diffusion for different original pressure |
由图 5可知,储层压力越低,受扩散作用影响越显著,以生产5 a时的产量增加值为例,最大可达到900 m
对页岩气藏来说,随着储层深度的增加,气藏的压力、温度都会改变,从而扩散作用对气井生产的影响也不同。设气井垂直井筒流压梯度为0.20 MPa/100 m,井口油压为1.00 MPa,地层压力系数为1;地层温度梯度为3℃/100 m,地面温度为20℃,应用产能公式计算扩散作用影响的最大孔隙直径见表 4。
| 表4 不同深度条件下扩散作用影响的最大孔径 Table 4 The max pore diameter affected by diffusion for different depth of the reservoir |
由表 4可知:随着储层深度的增加,扩散作用影响的最大孔隙直径减小,亦即,对较深储层而言,扩散作用的影响要小于浅层。
4 结论(1)建立的模型产量公式可应用于页岩气藏压裂水平井的考虑扩散作用的理论预测和因素分析。
(2)储层压力条件下,克努森系数受压力的影响变小,孔隙大小起主要作用。孔隙越小,克努森系数越大,扩散作用越大
(3)克努森系数可以评价扩散的影响程度,但在页岩气藏产量分析时,应考虑渗透率的增加程度来分析扩散影响程度。
(4)给出了不同深度页岩气藏压裂水平井考虑扩散作用时的孔隙直径范围。
(5)可根据渗透率、孔隙度、孔隙直径三者的近似关系综合分析扩散影响的适用范围,下一步需要给出考虑扩散作用的定量化建议。
符号说明
p——压力,MPa;
m,f,F——基质系统,裂缝网络系统,主裂缝系统。
| [1] | Soeder D J. Porosity and permeability of eastern devonian gas shale[C]. SPE Formation Evaluation, 1988, 3(1):116-124. http://www.osti.gov/scitech/biblio/7244188 |
| [2] | Javadpour J. Nanopores and apparent permeability of gasflow in mudrocks(shales and siltstone)[J]. Journal of Canadian Petroleum Technology, 2009, 48 (8) : 16 –21. DOI:10.2118/09-08-16-DA |
| [3] |
周玉辉, 张烈辉, 闫玉乐. 页岩气藏相渗规律研究[J].
新疆石油地质, 2013, 34 (4) : 445 –447.
Zhou Yuhui, Zhang Liehui, Yan Yule. A Study of relative permeability regularity in shale gas reservoirs[J]. Xinjiang Petroleum Geology, 2013, 34 (4) : 445 –447. |
| [4] |
程远方, 李友志, 时贤. 页岩气体积压裂缝网模型分析及应用[J].
天然气工业, 2013, 33 (9) : 53 –60.
Cheng Yuanfang, Li Youzhi, Shi Xian. Analysis and application of fracture network models of volume fracturing in shale gas reservoir[J]. Natural gas industry, 2013, 33 (9) : 53 –60. |
| [5] |
李海平, 贾爱林, 何东博, 等. 中国石油的天然气开发技术进展及展望[J].
天然气工业, 2010, 30 (1) : 5 –7.
Li Haiping, Jia Ailin, He Dongbo. Technical progress and outlook of natural gas development for the PetroChina[J]. Natural Gas Industry, 2010, 30 (1) : 5 –7. |
| [6] |
程远方, 董丙响, 时贤. 页岩气藏三孔双渗模型的渗流机理[J].
天然气工业, 2012, 32 (9) : 44 –48.
Cheng Yuanfang, Dong Bingxiang, Shi Xian. Seepage mechanism of a triple-porosity dual-permeability model for shale gas reservoirs[J]. Natural Gas Industry, 2012, 32 (9) : 44 –48. |
| [7] |
何学秋, 聂百胜. 孔隙气体在煤层中扩散的机理[J].
中国矿业大学学报, 2001, 30 (1) : 1 –4.
He Xueqiu, Nie Baisheng. Diffusion Mechanism of Porous Gases in Coal Seams[J]. Journal of China University of Mining & Technology, 2001, 30 (1) : 1 –4. |
| [8] |
盛茂, 李根胜, 黄中伟, 等. 考虑表面扩散作用的页岩气瞬态流动模型[J].
石油学报, 2014, 35 (2) : 347 –351.
Sheng Mao, Li Gensheng, Huang Zhongwei, et al. Shale gas transient flow model with effects of surface diffusion[J]. Acta Petrolei Sinica, 2014, 35 (2) : 347 –351. |
| [9] |
陈富勇, 琚宜文, 李小诗, 等. 构造煤中煤层气扩散渗流特征及其机理[J].
地学前缘, 2010, 17 (1) : 195 –201.
Chen Fuyong, Ju Yiwen, Li Xiaoshi, et al. Diffusionosmosis characteristics of coalbed methane in tectonically deformed coals and their mechanism[J]. Earth Science Frontiers, 2010, 17 (1) : 195 –201. |
| [10] |
杨建, 康毅力, 桑宇, 等. 致密砂岩天然气扩散能力研究[J].
西南石油大大学学报:自然科学版, 2009, 31 (6) : 76 –79.
Yang Jian, Kang Yili, Sang Yu, et al. Research on diffusibility of the gas in tight sand gas reservoir[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2009, 31 (6) : 76 –79. |
| [11] |
陈尚斌, 朱炎铭, 王红岩, 等. 川南龙马溪组页岩气储层纳米孔隙结构特征及其成藏意义[J].
煤炭学报, 2012, 32 (5) : 775 –782.
Chen Shangbin, Zhu Yanming, Wang Hongyan, et al. Structure characteristics and accumulation significance of nanopores in Longmaxi shale gas reservoir in the Southern Sichuan Basin[J]. Journal of China Coal, 2012, 32 (5) : 775 –782. |
| [12] | Javadpour F, Fisher D, Unsworth M. Nanoscale gas flow in shale gas sediments[J]. Journal of Canadian Petroleum Technology, 2007, 46 (10) : 55 –61. |
| [13] | Thorstenson D C, Pollock D W. Gas transport in unsaturated porous media:The adequacy of Fick's law[J]. Reviews of Geophysics, 1989, 27 (1) : 61 –78. DOI:10.1029/RG027i001p00061 |
| [14] |
田冷, 肖聪, 刘明进, 等. 考虑页岩气扩散的多级压裂水平井产能模型[J].
东北石油大学学报, 2014, 38 (5) : 93 –102.
Tian Leng, Xiao Cong, Liu Mingjin, et al. Productivity model for multi-stage fractured horizontal well for shale gas reservoir taking diffusion into consideration[J]. Journal of Northeast Petroleum University, 2014, 38 (5) : 93 –102. |
| [15] | 林瑞泰. 多孔介质传热传质引论[M]. 北京: 科学出版社, 1995 . |
| [16] | 时钧. 化学工程手册(1)[M]. 北京: 化学工业出版社, 1996 . |
| [17] |
聂百盛, 张力, 马文芳. 煤层甲烷在煤孔隙中扩散的微观机理[J].
煤田地质与勘探, 2000, 28 (6) : 20 –22.
Nie Baisheng, Zhang Li, Ma Wenfang. Diffusion micromechanism of coal bed methane in coal proes[J]. Coal Geology & Exploration, 2000, 28 (6) : 20 –22. |
| [18] |
赵孟军, 宋岩, 柳少波, 等. 扩散作用对天然气成藏后的影响——以大宛齐油田为例[J].
天然气地球科学, 2003, 14 (5) : 393 –397.
Zhao Mengjun, Song Yan, Liu Shaobo, et al. The diffusion influence on gas pool:Dawanqi Oilfield as an example[J]. Natural Gas Geoscience, 2003, 14 (5) : 393 –397. |
| [19] | Florence F A, Rushing J A, Newsham K E, et al. Improved permeability prediction relations for low permeability sands[C]. SPE 107954, 2007. http://www.pe.tamu.edu/blasingame/data/0_TAB_Public/TAB_Publications/SPE_107954_(Florence)_Improved_Permeability_Pred_Relations_Low_Perm_Sands.pdf |
| [20] | Villazon G G M, Sigal R F, Civan F, et al. Parametric investigation of shale gas production considering nanoscale pore size distribution, formation factor, and non-darcy flow mechanisms[C]. SPE 147438, 2011. |
 2015, Vol. 37
2015, Vol. 37


