2. EMS Energy Institute and G3 Center, Pennsylvania State University, University Park, 16802, USA
2. EMS Energy Institute and G3 Center, Pennsylvania State University, University Park, 16802, USA
支撑裂缝的渗透率是评价水力压裂作业效果的重要指标,裂缝闭合时,支撑剂由于硬度较高,在围压的作用下嵌入裂缝壁面,造成裂缝宽度的损失和渗透率的下降,以往学者[1-8]针对支撑剂嵌入机理进行了大量的实验和数值模拟研究,讨论了闭合压力、地层弹性模量、支撑剂粒径等参数的影响规律,其中,卢聪等[5]的实验结果表明,嵌入作用能使导流能力下降20%~50%,因此,支撑剂的嵌入是影响支撑裂缝渗透率的重要因素之一。
此外,CO2、CH4等吸附性气体吸附于岩石孔隙和岩石基质中,将使岩石的体积膨胀,对渗透率同样具有显著影响。这种溶胀作用在煤岩中尤为明显,Hemant Kumar等[9-10]、Levine J R[11]、Chikatamarla L[12-13]、Ravikoviteh P I[14]等学者,分别采用实验和数值模拟的方法,研究了煤岩基质膨胀对裂缝渗透率的影响。而对于页岩,类似的吸附机理同样存在,文献[15-18]分别从CO2驱替、埋存等工程角度出发,研究了页岩中的气体吸附特性。但由于页岩远比煤岩致密,页岩吸附后的体积膨胀,以及页岩中溶胀作用对渗透率影响的相关研究较少。本文以页岩中支撑裂缝的渗透率为研究对象,通过实验手段,探索页岩中吸附溶胀作用和支撑剂嵌入作用对渗透率的影响。
1 实验装置渗透率测量实验装置[19],如图 1所示,由注射泵组、岩芯夹持器、储气室以及数据采集系统等组成。ISCO 500D型高压注射泵组通过注水,可以为岩芯提供最高35 MPa的轴压和围压,泵压控制精度为±0.007 MPa,具有恒压注入和恒流速注入两种模式;直径2.5 cm,长5.0 cm的标准页岩岩样,首先被包裹在耐高压的橡胶套中进行密封,再由Temco岩芯夹持器夹持,并施加轴压和围压;储气室共分上下游两个,上游体积为26.70 mL,下游体积为16.83 mL,气室的出口分别连接有压力传感器,用于测量和记录实验过程中气室内的压力值;压力传感器的电压信号通过一个16通道的数据采集盒(National Instruments-USB 6211)接收和转化,数据采集盒通过USB与电脑连接,实验过程中的压力数据在Labview软件平台中记录,该软件平台同时集成了泵组的控制功能。
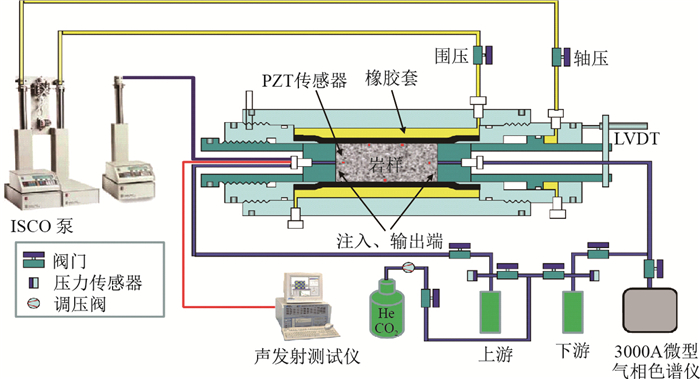 |
| 图1 脉冲法测量渗透率实验流程图 Fig. 1 Schematic of permeability measurement using pulse test method |
本次实验选用的吸附气体是纯度为99.995%的CO2,非吸附气体选用纯度为99.999%的He;页岩岩样选用Greenriver页岩,标准尺寸为直径2.5 cm,长5.0 cm,固定碳含量5%~8%,灰分产量87%~92%,水分含量0.5%~1.0%,内聚力强度约10 MPa;参照岩样选用Westerly花岗岩,同样为标准尺寸;支撑剂选用40/80目的Carbo陶粒,颗粒粒径为0.177~0.400 mm。实验轴压和围压同为25 MPa,实验温度为室温23 ℃,注气压力为2~9 MPa,测量系统的采集频率为100 Hz。
在实验准备阶段,将标准尺寸的岩芯沿轴向切成对称的两半,页岩岩芯的切面用细砂纸进行打磨抛光,花岗岩由于硬度高,需要用极细的金属铝粒进行打磨抛光,如图 2所示,在抛光后的岩芯表面均匀平铺一层支撑剂颗粒,再将两半岩芯重新拼接,支撑剂被夹在两半岩芯中间,从而形成一个人工模拟的支撑裂缝,将重新拼接的岩芯用铝箔进行包裹,再用胶带进行密封,将包裹好的岩芯放入耐高压橡胶套内,最后放入岩芯夹持器内进行实验。
 |
| 图2 实验准备阶段的岩样加工和包裹 Fig. 2 The sample processing and packaging before experiment |
本次研究设计了3组不同气体和岩样的实验,通过实验结果的相互比对,揭示支撑剂嵌入和吸附气体溶胀作用对渗透率的影响。
(1)He在花岗岩支撑裂缝中的渗透率实验
由于花岗岩硬度高,支撑剂不发生嵌入作用,该组实验即不存在支撑剂的嵌入作用,也不存在吸附气体的溶胀作用。
(2)He在页岩支撑裂缝中的渗透率实验
页岩强度低于支撑剂强度,且He为非吸附性气体,因此,该组实验存在支撑剂的嵌入作用,但不存在吸附气体的溶胀作用。
(3)CO2在页岩支撑裂缝中的渗透率实验
该组实验同时包含支撑剂的嵌入和吸附气体的溶胀作用。
采用Pulse test(脉冲测试法)实验方法[10],测量He和CO2在支撑裂缝中的渗透率:首先进行管线流程的气密性检查,再进行轴压和围压的注水加压测试。测试完成后对系统内进行抽真空,并施加25 MPa的轴压和围压开始实验。关闭上游气室的出口,将一定压力的气体注入上游气室,与下游形成一个压力差,待压力稳定后,打开上游气室的出口,气体在压差作用下,从上游气室经过岩芯裂缝到达下游气室,并最终达到压力平衡,记录平衡过程中,上下游气室压力值的变化,裂缝内的渗透率通过以下公式进行计算
| $ K=\dfrac{{\gamma \mu LV_{{\rm{u}}} V_{{\rm{d}}} }}{{p_{{\rm{eq}}} A(V_{{\rm{u}}}+V_{{\rm{d}}})}} $ | (1) |
式中:
K-渗透率,D;
γ-衰减系数,s-1;
µ-气体的黏度,Pa·s;
L-岩芯长度,m;
Vu,Vd-上、下游气室的体积,m3;
peq-系统平衡后的压力,MPa;
A-气体的过流断面,m2。
对实验过程中单位时间内上、下游气室的压差与初始时刻气室的压差的比值取对数,并作关于时间的曲线,得到的曲线为直线,衰减系数γ就是这条直线的斜率
| $ \gamma=\dfrac{{\lg \left[{\dfrac{{{\rm{d}}(p_{{\rm{u}}}-p_{{\rm{d}}})}}{{p_{{\rm{u}}}^0-p_{{\rm{d}}}^0 }}} \right]_{\rm{t}} }}{{{\rm{d}}t}} $ | (2) |
式中:
pu,pd-单位时间内上、下游气室的压力,MPa;
p u0,p u0-初始时刻上、下游气室的压力,MPa。
为了提高实验结果的准确性,对每个压力下的渗透率进行了3次重复测量,并将测量结果全部绘制在渗透率曲线中。特别地,注气压力的变化采用了由低压到高压,再反向由高压到低压的双向重复测量方法,进一步消除了不确定因素对结果的影响。本次研究的渗透率曲线表现出了良好的稳定性和可重复性,因此,实验结果准确可靠。
4 实验结果及分析 4.1 He在花岗岩支撑裂缝中的渗透率实验结果He在花岗岩的渗透率随着注气压力的增加呈线性趋势增加,如图 3所示,注气压力的增加导致裂缝的有效应力降低,因而气体的渗透率增加。由于花岗岩的强度较高,支撑剂在25 MPa围压作用下,受力不均匀的颗粒发生了破碎,从而也说明了花岗岩实验中不存在支撑剂的埋置作用,实验前后的花岗岩岩样对比如图 4所示。
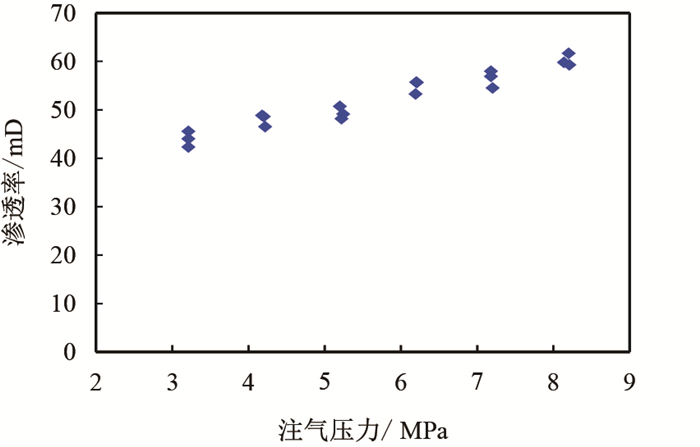 |
| 图3 He在花岗岩支撑裂缝中的渗透率变化 Fig. 3 The permeability evolution of He in propped westerly granite |
 |
| 图4 实验前后的花岗岩岩样对比 Fig. 4 The granite sample before and after experiment |
He在页岩中的渗透率明显低于在花岗岩中的渗透率,如图 5所示,支撑剂的嵌入作用导致裂缝的有效缝宽变窄,从而导致渗透率降低,与花岗岩相比,页岩由于支撑剂的嵌入作用损失了约50%左右的渗透率,可见,嵌入作用对渗透率的影响十分明显。
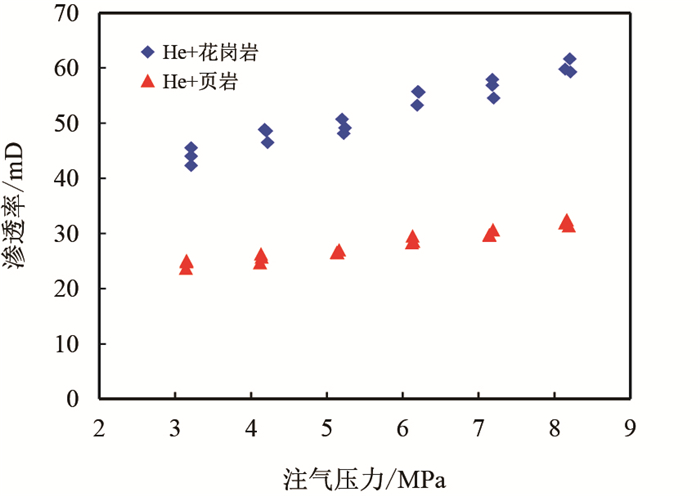 |
| 图5 He在页岩支撑裂缝中的渗透率变化 Fig. 5 The permeability evolution of He in propped shale |
对比实验前后页岩岩芯的表面,如图 6所示,图 6a为实验前经过砂纸打磨的岩芯壁面,图 6b为实验后裂缝的壁面,在25 MPa围压的作用下,支撑剂的嵌入,对岩芯表面的破坏作用十分明显。
 |
| 图6 支撑剂嵌入对岩样表面的破坏作用 Fig. 6 The damage in the sample surface due to the proppant embedment |
CO2在页岩中的渗透率,随着注气压力的增加呈现典型的“U”型曲线,与吸附气体在煤岩中的渗透率曲线变化规律相同,说明CO2的吸附溶胀作用对渗透率起到了显著影响,如图 7所示,注气压力的升高使渗透率增加,而CO2吸附溶胀作用使渗透率降低,在两种机理的共同作用下,渗透率的变化曲线呈现“U”型。
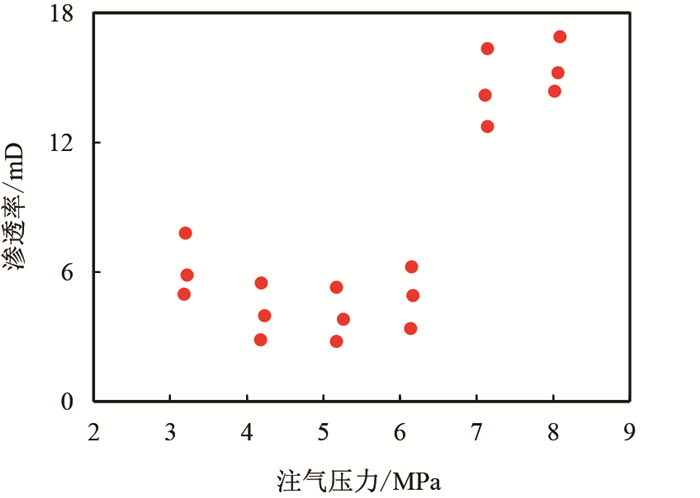 |
| 图7 CO2在页岩支撑裂缝中的“ U”型渗透率曲线 Fig. 7 The U shape of CO2 permeability curve in propped shale |
CO2在页岩中的吸附特性符合Langmuir等温吸附模型,即气体的吸附量随着压力的升高而增大,当压力高于某一压力值时,气体的吸附量达到最大,此后保持恒定,这一压力值称为Langmuir压力。在图 7的渗透率变化曲线中,当注气压力较低时,气体大量吸附,溶胀作用加剧,有效缝宽被膨胀的岩石侵蚀,渗透率降低。当气压小于5 MPa时,气体的吸附溶胀作用占主导地位,因而渗透随气压的升高呈下降趋势;当气压在5 MPa附近时,气体的吸附量达到最大值,此时的渗透率也达到了最小值;当气压大于5 MPa时,气体的吸附量不再继续增加,而注气压力的升高,导致有效应力减小,并开始主导渗透率的变化,因此,渗透率呈现上升趋势。
以上分析表明,在本次实验的温度、压力条件下,CO2在页岩中的Langmuir压力约为5 MPa,这一结论与孙宝江等在30℃下进行的CO2吸附页岩实验结果吻合[20]。
4.4 溶胀和嵌入作用对渗透率的影响规律分析如图 8所示,将He在花岗岩、页岩以及CO2在页岩中的渗透率实验结果进行比对,结果表明,非吸附性气体的渗透率变化呈线性,而吸附气体,由于影响渗透率的机理复杂,渗透率变化曲线呈非线性;与花岗岩相比,页岩由于支撑剂的嵌入作用,渗透率降低了约50%,与He相比,CO2使页岩的渗透率进一步降低,特别是注气压力在Langmuir压力附近时,渗透率由25 mD左右,降低至5 mD左右,降幅约80%,当压力大于Langmuir压力时,渗透率得到了一定的恢复。
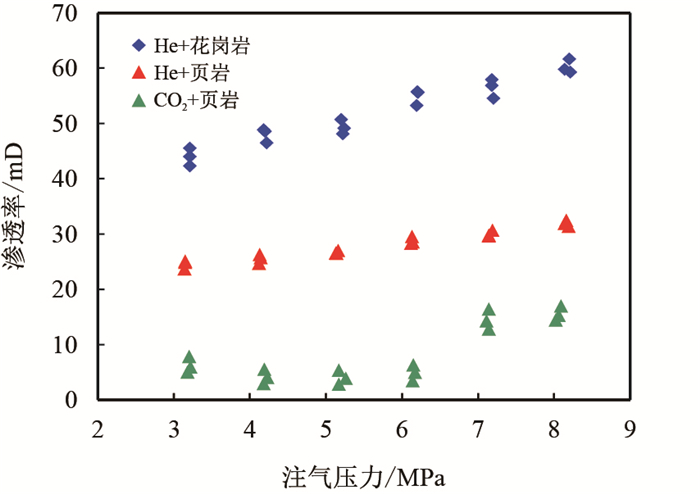 |
| 图8 He、CO2在花岗岩和页岩中的渗透率变化对比图 Fig. 8 Comparisons of He permeability in granite and shale and CO2 permeability in shalee |
值得注意的是,图 8中,He和CO2在页岩中的渗透率差异,并非单纯的由吸附溶胀作用引起的,CO2的吸附溶胀作用一方面使岩石膨胀,裂缝宽度减小,另一方面还降低了岩石的强度,而岩石强度的降低势必进一步加重支撑剂的嵌入作用,因此,溶胀对嵌入的影响有必要进一步通过实验探索。
实验结果的分析表明,在页岩中,吸附气体的溶胀作用同样会影响渗透率,且由此损失的渗透率值较大。与CO2类似,甲烷也是典型的吸附性气体,因此,在页岩气藏的开发中,溶胀作用对渗透率的影响应当予以重视,特别是在生产过程中,应保障气藏压力尽量远离Langmuir压力。
5 结论(1)采用Pulse test实验方法,测量了非吸附气体He和吸附气体CO2在Greenriver页岩和Westerly花岗岩支撑裂缝中的渗透率,其中,支撑剂的嵌入作用使He在页岩中的渗透率与花岗岩相比,降低了约50%。
(2)通过实验方法,研究了CO2吸附气体对Greenriver页岩支撑裂缝渗透率的影响,结果表明,CO2渗透率曲线呈典型的“U”型,与吸附气体在煤岩中的渗透率曲线变化规律相同,从而说明吸附溶胀作用对页岩支撑裂缝的渗透率同样有显著影响,并且CO2渗透率在Langmuir压力值附近达到最小值。
(3)对比分析He和CO2在页岩支撑裂缝中的渗透率曲线,结果表明,非吸附气体的渗透率主要由有效应力主导,曲线呈线性变化,而吸附气体的渗透率受溶胀作用和有效应力的双重影响,曲线呈“U”型变化,且溶胀作用的存在比单纯的支撑剂嵌入作用更能降低渗透率。
| [1] |
赵金洲, 何弦桀, 李勇明. 支撑剂嵌入深度计算模型[J].
石油天然气学报, 2014, 36 (12) : 209 –212.
Zhao Jinzhou, He Xianjie, Li Yongming. A calculation model of proppant embedment depth[J]. Journal of Oil and Gas Technology, 2014, 36 (12) : 209 –212. |
| [2] |
郭建春, 卢聪, 赵金洲, 等. 支撑剂嵌入程度的实验研究[J].
煤炭学报, 2008, 33 (6) : 661 –664.
Guo Jianchun, Lu Cong, Zhao Jinzhou, et al. Experimental research on proppant embedment[J]. Journal of China Coal Society, 2008, 33 (6) : 661 –664. |
| [3] |
郭天魁, 张士诚. 影响支撑剂嵌入的因素研究[J].
断块油气田, 2011, 18 (4) : 527 –529, 544.
Guo Tiankui, Zhang Shicheng. Study on the factors affecting proppant embedment[J]. Fault-Block Oil & Gas Field, 2011, 18 (4) : 527 –529, 544. |
| [4] |
胡智凡, 卢渊, 伊向艺, 等. 单层铺砂条件下支撑剂嵌入深度对裂缝导流能力影响实验研究[J].
科学技术与工程, 2014, 14 (5) : 232 –234, 246.
Hu Zhifan, Lu Yuan, Yi Xiangyi, et al. Under the condition of single sanding closure pressure affecting proppant embed depth study[J]. Science Technology and Engineering, 2014, 14 (5) : 232 –234, 246. |
| [5] |
卢聪, 郭建春, 王文耀, 等. 支撑剂嵌入及对裂缝导流能力损害的实验[J].
天然气工业, 2008, 28 (2) : 99 –101.
Lu Cong, Guo Jianchun, Wang Wenyao, et al. Experimental research on proppant embedment and its damage to fractures conductivity[J]. Natural Gas Industry, 2008, 28 (2) : 99 –101. |
| [6] |
吴国涛, 胥云, 杨振周, 等. 考虑支撑剂及其嵌入程度对支撑裂缝导流能力影响的数值模拟[J].
天然气工业, 2013, 33 (5) : 65 –68.
Wu Guotao, Xu Yun, Yang Zhenzhou, et al. Numerical simulation considering the impact of proppant and its embedment degree on fracture flow conductivity[J]. Natural Gas Industry, 2013, 33 (5) : 65 –68. |
| [7] |
赵阳升, 胡耀青, 杨栋, 等. 三维应力下吸附作用对煤岩体气体渗流规律影响的实验研究[J].
岩石力学与工程学报, 1999, 18 (6) : 651 –653.
Zhao Yangsheng, Hu Yaoqing, Yang Dong, et al. The experimental study on the gas seepage law of rock related to adsorption under 3-D stress[J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18 (6) : 651 –653. |
| [8] |
温庆志, 张士诚, 王雷, 等. 支撑剂嵌入对裂缝长期导流能力的影响研究[J].
天然气工业, 2005, 25 (5) : 65 –68.
Wen Qingzhi, Zhang Shicheng, Wang Lei, et al. Influence of proppant embedment on fracture long-term flow conductivity[J]. Natural Gas Industry, 2005, 25 (5) : 65 –68. |
| [9] | Hemant Kumar, Derek Elsworth, Jonathan P, et al. Effect of CO2 injection on heterogeneously permeable coalbed reservoirs[J]. Fuel, 2014, 135 (1) : 509 –521. |
| [10] | Hemant Kumar, Derek Elsworth, Jishan Liu, et al. Optimizing enhanced coalbed methane recovery for unhindered production and CO2 injectivity[J]. International Journal of Greenhouse Gas Control, 2012, 11 : 86 –97. DOI:10.1016/j.ijggc.2012.07.028 |
| [11] | Levine J R. Model study of the influence of matrix shrinkage permeability of coal bed reservoirs[J]. Geological Society, 1996, 109 (1) : 197 –212. DOI:10.1144/GSL.SP.1996.109.01.14 |
| [12] | Chikatamarla L, Cui X, Bustin R M. Implications of volumetric swelling/shrinkage of coal in sequestration of acid gases[C]//Coalbed Methane Symposium, Tuscaloosa, AL.2004. |
| [13] | Xiaojun Cui, Bustin R M, Laxmi Chikatamarla. Adsorption-induced coal swelling and stress:Implications for methane production and acid gas sequestration into coal seams[J]. Journal of Geophysical Research: Solid Earth, 2007, 112 (B10) . |
| [14] | Ravikoviteh P I, Neimark A V. Density functional theory model of adsorption on amorphous and microporous silica material[J]. Langmuir, 2006, 22 (6) : 11171 –11179. |
| [15] |
熊伟, 郭为, 刘洪林, 等. 页岩的储层特征以及等温吸附特性[J].
天然气工业, 2012, 32 (1) : 113 –116.
Xiong Wei, Guo Wei, Liu Honglin, et al. Shale reservoir characteristics and isothermal adsorption properties[J]. Natural Gas Industry, 2012, 32 (1) : 113 –116. |
| [16] | Daniel JKR, Bustin R M. The importance of shale composition and pore structure upon gas storage potential of shale gas reservoirs[J]. Marine and Petroleum Geology, 2009, 26 (6) : 916 –927. DOI:10.1016/j.marpetgeo.2008.06.004 |
| [17] | Andreas B, Sascha A, Yves G, et al. Carbon dioxide storage potential of shales[J]. International Journal of Greenhouse Gas Control, 2008, 2 (3) : 297 –308. DOI:10.1016/j.ijggc.2008.03.003 |
| [18] | Tongwei Zhang, Geoffrey S Ellis, Stephen C Ruppel, et al. Effect of organic-matter type and thermal maturity on methane adsorption in shale-gas systems[J]. Organic Geochemistry, 2012, 47 : 120 –131. DOI:10.1016/j.orggeochem.2012.03.012 |
| [19] | Shugang Wang, Derek Elsworth, Jishan Liu. Permeability evolution in fractured coal:The roles of fracture geometry and water-content[J]. International Journal of Coal Geology, 2011, 87 (1) : 13 –25. DOI:10.1016/j.coal.2011.04.009 |
| [20] |
孙宝江, 张彦龙, 杜庆杰, 等. CO2在页岩中的吸附解吸性能评价[J].
中国石油大学学报:自然科学版, 2013, 37 (5) : 95 –99, 106.
Sun Baojiang, Zhang Yanlong, Du Qingjie, et al. Property evaluation of CO2 adsorption and desorption on shale[J]. Journal of China University of Petroleum, 2013, 37 (5) : 95 –99, 106. |
 2015, Vol. 37
2015, Vol. 37


