2. 中国石油大庆油田有限责任公司第八采油厂, 黑龙江 大庆 163000
2. No. 8 Oil Production Company of Daqing Oil-field Company Ltd., Daqing, Heilongjiang 163000, China
目前,确定待测井曲线类型的方法均基于试井基本原理[1-2],通过预设一组参数,选取相应的试井模型,绘制理论曲线,最后通过测试时间确定出曲线类型。其预测的曲线类型与预设一组参数和选取的模型有直接的关系,且试井曲线对参数和模型敏感性极强,微小的变动将会出现不同的结果。因此在很多低渗透油藏实测的试井曲线往往与预期的试井设计大相径庭[3]。
判别分析[4-7]是多元统计学中用来确定未知样品所属类型的一种统计分析方法,以实际样品数据为依据,分析其共性,对新样本进行判别分类,克服了理想假设情况以及实测过程中的系统误差。白玉峰等[8]借助于判别分析对心血管功能进行定量地判别与预测,张成虎等[9]基于个人消费信贷数据,建立个人信用评分的线性判别模型。田方等[10]利用逐步判别分析方法,建立了各油田的砂泥岩剖面油水判别函数,定量地确定地层的油、水性质,提高测井解释精度。王研等[11]应用判别分析数学原理,并利用气测录井资料,建立了快速识别松辽盆地东南隆起区油、气、水层判别模型。该方法已在自然科学和社会科学的各个领域得到广泛应用[12-15],包括医学、经济学、环境科学、地质学等领域的多个层面,但尚未在试井曲线类型判别上应用。本文根据油田实测试井曲线,并将其分为:井储型、驼峰型、径向流型和上翘型,利用多组判别分析方法,最终建立了曲线类型判别模型。从已用曲线类型出发,预测的曲线类型更贴合实际情况,选取的参数已明确固定,人为主观因素影响小,可帮助快速判断压力曲线类型,优化监测方案,减少井储型监测井监测比例。在八厂油田实际试井中进行曲线类型预测运用,取得了良好的效果。
1 多组判别分析方法 1.1 方法原理多组判别法的基本思想是基于统计上的费舍准则,即判别的结果应该使多组间区别最大,使每组内部离散性最小。在费舍准则意义下,确定线性判别函数
| $ y(x) = c_1 x_1 + c_2 x_2 + \cdots c_p x_p $ | (1) |
式中:
判别函数系数的确定原则是使两组间区别最大,使每组内部离散性最小。有了判别函数后,对于每一个新的样品,将
设有
假定所建立的判别函数为
| $ y(x) = c_1 x_1 + c_2 x_2 + \cdots c_p x_p \buildrel \Delta \over = {{\boldsymbol{c}}}'{{\boldsymbol{x}}} $ | (2) |
式中:
| $ {\bf{c}} = \left[ {{c_1}{\rm{,}}{c_2}{\rm{,}} \cdots {\rm{,}}{c_p}} \right]',{\bf{x}} = \left[ {{x_1}{\rm{,}}{x_2}{\rm{,}} \cdots {\rm{,}}{x_p}} \right]' $ |
根据求随机变量线性组合的均值和方差的性质可知,
| $ \overline y ^{(i)} = {{\boldsymbol{c}}}'\overline {{\boldsymbol{x}}} ^{(i)}, \sigma _i^2 = {{\boldsymbol{c}}}'s^{(i)} {{\boldsymbol{c}}} $ | (3) |
式中:
记
在多总体情况下,多组判别准则就是要选取系数向量
| $ \lambda = \dfrac{{\sum\limits_{i = 1}^k {n_i (\overline y ^{(i)} - \overline y )^2 } }}{{\sum\limits_{i = 1}^k {q_i \sigma _i^2 } }} $ | (4) |
式中:
如果取
| $ \lambda = \dfrac{{{{\boldsymbol{c}}}'{{\boldsymbol{A}}}{{\boldsymbol{c}}}}}{{{{\boldsymbol{c}}}'{{\boldsymbol{E}}}{{\boldsymbol{c}}}}} = \dfrac{{{{\boldsymbol{c}}}'\sum\limits_{i = 1}^k {n_i (\overline {{\boldsymbol{x}}} ^{(i)} - \overline {{\boldsymbol{x}}} )} (\overline {{\boldsymbol{x}}} ^{(i)} - \overline {{\boldsymbol{x}}} )'{{\boldsymbol{c}}}}}{{{{\boldsymbol{c}}}'\sum\limits_{i = 1}^k {q_i s^{(i)} } {{\boldsymbol{c}}}}} $ | (5) |
式中:
为求
利用对向量求导的公式
| $ \begin{array}{c} \dfrac{{\partial \lambda }}{{\partial {{\boldsymbol{c}}}}} = \dfrac{{2{{\boldsymbol{A}}}{{\boldsymbol{c}}}}}{{({{\boldsymbol{c}}}'{{\boldsymbol{E}}}{{\boldsymbol{c}}})^2 }} \cdot ({{\boldsymbol{c}}}'{{\boldsymbol{E}}}{{\boldsymbol{c}}}) - \dfrac{{2{{\boldsymbol{E}}}{{\boldsymbol{c}}}}}{{({{\boldsymbol{c}}}'{{\boldsymbol{E}}}{{\boldsymbol{c}}})^2 }} \cdot ({{\boldsymbol{c}}}'{{\boldsymbol{A}}}{{\boldsymbol{c}}}) \\[8pt] = \dfrac{{2{{\boldsymbol{A}}}{{\boldsymbol{c}}}}}{{{{\boldsymbol{c}}}'{{\boldsymbol{E}}}{{\boldsymbol{c}}}}} - \dfrac{{2{{\boldsymbol{E}}}{{\boldsymbol{c}}}}}{{{{\boldsymbol{c}}}'{{\boldsymbol{E}}}{{\boldsymbol{c}}}}} \cdot \dfrac{{{{\boldsymbol{c}}}'{{\boldsymbol{A}}}{{\boldsymbol{c}}}}}{{{{\boldsymbol{c}}}'{{\boldsymbol{E}}}{{\boldsymbol{c}}}}} \\[8pt] = \dfrac{{2{{\boldsymbol{A}}}{{\boldsymbol{c}}}}}{{{{\boldsymbol{c}}}'{{\boldsymbol{E}}}{{\boldsymbol{c}}}}} - \dfrac{{2{{\boldsymbol{E}}}{{\boldsymbol{c}}}}}{{{{\boldsymbol{c}}}'{{\boldsymbol{E}}}{{\boldsymbol{c}}}}} \cdot \lambda \\ \end{array} $ | (6) |
因此
| $ \dfrac{{\partial \lambda }}{{\partial {{\boldsymbol{c}}}}} = 0 \Rightarrow \dfrac{{2{{\boldsymbol{A}}}{{\boldsymbol{c}}}}}{{{{\boldsymbol{c}}}'{{\boldsymbol{E}}}{{\boldsymbol{c}}}}} - \dfrac{{2\lambda {{\boldsymbol{E}}}{{\boldsymbol{c}}}}}{{{{\boldsymbol{c}}}'{{\boldsymbol{E}}}{{\boldsymbol{c}}}}} = 0 \Rightarrow {{\boldsymbol{A}}}{{\boldsymbol{c}}} = \lambda {{\boldsymbol{E}}}{{\boldsymbol{c}}} $ | (7) |
这说明
| $ \lambda _1 \geqslant \lambda _2 \geqslant \cdots \geqslant \lambda _m > 0 $ | (8) |
于是可构造
| $ y_l (x) = {{\boldsymbol{c}}}^{(l)^{'}} x\begin{array}{*{20}c} {} & {} & {} \\ \end{array}l = 1, 2, \cdots, m $ | (9) |
式中:
对于每一个判别函数必须给出一个
| $ p_l = \dfrac{{\lambda _l }}{{\sum\limits_{l = 1}^m {\lambda _l } }}\begin{array}{*{20}c} {} & {} & {} \\ \end{array}l = 1, 2, \cdots, m $ | (10) |
式中:
| $ \overline y _l^{(i)} = {{\boldsymbol{c}}}^{(l)'} \overline {{\boldsymbol{x}}} ^{(i)} \begin{array}{*{20}c} {} & {} & {} \\ \end{array}l = 1, \cdots, m;i = 1, \cdots, k $ | (11) |
对待判别样品
| $ D_i^2 = \sum\limits_{l = 1}^m {\left[{y_l (x)-\overline y _l^{(i)} } \right]^2 \begin{array}{*{20}c} {} & {} & {} \\ \end{array}i = 1, 2, \cdots, k} $ | (12) |
若
式中:
考虑每个判别函数的判别能力不同,记
| $ D_i^2 = \sum\limits_{l = 1}^m {\left[{y_l \left( x \right)-\overline y _l^{\left( i \right)} } \right]} ^2 \lambda _l $ | (13) |
为了检验
| $ D^2 = \sum\limits_{i = 1}^p {\sum\limits_{j = 1}^p {\sum\limits_{l = 1}^m {n_l \cdot s_{ij}^{ - 1} \left( {\overline x _i^{(l)} - \overline {{\boldsymbol{x}}} _i } \right)} } } \left( {\overline x _j^{(l)} - \overline x _j } \right) $ | (14) |
统计量
在建立多个总体的判别函数后,可将已知类别的样品代入判别函数进行回判。如果错判率在25%以下,则可以认为判别函数是有效的,否则认为模型是无效的。其常用的计算公式为
| $ \mbox{错判率}=\dfrac{\mbox{判错的样品数}}{\mbox{总样品数}} $ | (15) |
大庆油田第八采油厂某油田为低渗透油藏,根据历年试井测压资料成果,设计试井关井时间为240h,但仅有小部分测试成果符合预期的试井设计,大大影响了试井测试经济效益。本文将利用多组判别分析原理,并结合大庆油田第八采油厂某油田录井、测井、钻完井等静态资料以及生产动态资料,选取典型井的参数作为样本,建立该油田的测试曲线类型判别模型,对该油田待测试井进行试井曲线类型预测,优化监测井点部署方案。
2.1 数据准备通过多组判别原理可知,要建立曲线类型预判模型,需明确组数(曲线类型)、变量(作为预判模型的静、动态参数)和已知样本(已有测试成果的井)。统计分析八厂某油田历年实测测试资料,其试井双对数曲线,主要分为4种曲线类型:径向流型、驼峰型、井储型和上翘型(图 1)。结合录井、测井、钻完井等静态资料以及生产动态资料等,最终选取四个参数(有效厚度、含水率、测井渗透率、产量)作为建立预判模型的变量参数,其参数优选的过程是用已知的开发参数作为基础数据,利用多组判别的方法逐步判断,选择预判错误率最低的一组数据作为预判模型的变量参数,这些参数包括厚度、含水率、产量、测井渗透率、体积系数和油粘度。本文利用变量数从6个逐渐减少为1个,选取共63次多组判别过程中,错判率最小的一组变量组合作为变量参数,各参数组合的错判率见表 1所示。
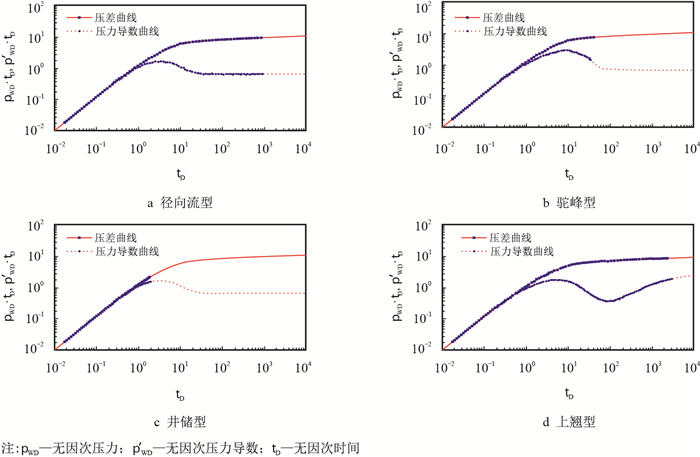 |
| 图1 四种曲线类型 Fig. 1 Four curve types |
| 表1 多组判别变量参数优选表 Table 1 Multi-group discriminant variable parameter optimization |
根据各测试井的地质情况、位置情况、参数完整性以及曲线类型等因素,优选出44口典型井(径向流型、驼峰型、井储型和上翘型),作为建立预判模型的样本。其44口典型井的基本参数数据见表 2。
| 表2 曲线类型预判模型样品数据及回代结果表 Table 2 The sample data of curve type forecasting model and back substitution results |
选取176个径向流型、驼峰型、井储型和上翘型的数据作为判别模型的已知样本,通过多组判别分析理论,构建一个判断八厂某油田测试井曲线类型的模型。其4种曲线类型的判别方程为
井储型
| $ y_1 (x) = - 111.565 + 7.384x_1 + 1.187x_2 +19.855x_3 + 1.295x_4 $ | (16) |
驼峰型
| $ y_2 (x) = - 71.188 + 5.793x_1 + 0.948x_2 + 14.966x_3 + 1.078x_4 $ | (17) |
径向流型
| $ y_3 (x) = - 74.255 + 6.833x_1 + 0.833x_2 + 13.447x_3 + 1.191x_4 $ | (18) |
上翘型
| $ y_4 (x) = - 121.548 + 8.415x_1 + 1.174x_2 + 18.613x_3 + 1.452x_4 $ | (19) |
为进一步验证建立模型的准确性,将作为样本的44口典型井数据回代入新建的试井曲线类型判别模型中,根据判别准则重新判别分类(回代曲线类型见表 2)。其重新判别确定的曲线类型与原曲线类型结果进行对比,见表 3所示。从表 3中可以看出,所建立的判别模型对径向流型、驼峰型、井储型和上翘型的识别能力强,其总的错判率为9.09%。计算获得的马氏统计量为
| 表3 回代验证错判结果表 Table 3 False rates verification results |
针对井5,实际监测结果为径向流型曲线,但是模型判断为上翘型,而井34实际监测结果为上翘型,但是模型判断为径向流型。其原因主要是:(1)两口井的地理位置非常相近,实际地下距离为270m;(2)两口井的试井解释结果相近,解释结果如表 4所示;(3)两井的实测试井双对数曲线均处于径向流型与上翘型的临界位置,如图 2所示。
| 表4 井5和井34试井解释结果 Table 4 The well-test results of well 5 and well 34 |
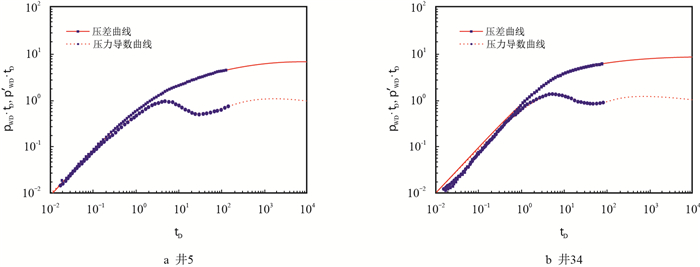 |
| 图2 井5和井34试井双对数曲线 Fig. 2 The Log-Log well-test curves of Well 5 and Well 34 |
对现场的试井解释而言,径向流型曲线和上翘型曲线都能够很准确地解释出地层参数。
综上所述,马氏统计量大于临界值,错判率在规定的精度内,建立的曲线类别模型较为准确可靠,可用有效厚度、含水率、测井渗透率、产量4个参数预判待测试井的曲线类型。
3 实测井曲线类型预测根据现场28口待测新井的数据资料,利用本文建立的判别模型进行试井测试曲线类型预判,其径向流型、驼峰型、井储型和上翘型分为5口、11口、4口和8口;将该预判结果与后期现场实际测试的结果进行了对比分析,如表 5所示,可以看出,用本文建立的模型预判新井的曲线类型,符合率达到85.7%,该预测模型符合率较高,可应用于现场对待测井曲线类型的预判。
| 表5 现场实例应用符合率检验结果表 Table 5 Field application of coincidence rates test results |
(1) 通过研究多组判别基本原理,结合低渗透油藏测试实际情况,获得了利用多组判别模型来预测测试曲线类型的方法。该方法操作简单、方便,基于实测已有的数据,更加符合油藏实际情况。
(2) 研究获得了利用有效厚度、含水率、测井渗透率、产量4个参数预判待测试井的曲线类型的判别模型,其马氏统计量大于临界值,错判率为9.09%,能较为准确地识别径向流型、驼峰型、井储型和上翘型4种曲线类型。
(3) 将建立的多组曲线类型预测模型,应用于大庆油田第八采油厂某油田28口测试井中,预测结果符合率为85.7%。研究成果可为现场工作人员优化监测井点部署提供科学依据,有效地提升监测成果质量。
| [1] | 林加恩. 实用试井分析方法[M]. 北京: 石油工业出版社, 1996 . |
| [2] | 刘能强. 实用现代试井解释方法[M]. 北京: 石油工业出版社, 2007 . |
| [3] |
杨秀祥, 程时清, 袁玉金, 等. 特低渗透油藏试井解释中的模型选择及油藏诠释[J].
油气井测试, 2007, 16 (2) : 14 –16.
Yang Xiuxiang, Cheng Shiqing, Yuan Yujin, et al. Well testing model selection and reservoir annotation to low permeability reservoirs[J]. Well Testing, 2007, 16 (2) : 14 –16. |
| [4] | 高惠璇. 应用多元统计分析[M]. 北京: 北京大学出版社, 2005 . |
| [5] | 范金城, 梅长林. 数据分析[M]. 北京: 科学出版社, 2002 . |
| [6] | Schrider L A, Byrd Jr J. Discriminant analysis as a technique for exploitation of petroleum reservoirs[C]//Fall Meeting of the Society of Petroleum Engineers of AIME, Society of Petroleum Engineers, 1971. |
| [7] | Nashawi I S, Malallah A. Permeability prediction from wireline well logs using fuzzy logic and discriminant analysis[C]. SPE 133209, 2010. |
| [8] | 白玉峰, 耿美英, 连江宏, 等. 逐步Bayes判别分析在心血管功能评定中的应用[J]. 北京工业大学学报, 1994, 20 (1) : 54 –60. |
| [9] |
张成虎, 李育林, 吴鸣. 基于判别分析的个人信用评分模型研究与实证分析[J].
大连理工大学学报:社会科学版, 2009, 30 (1) : 6 –10.
Zhang Chenghu, Li Yulin, Wu Ming. Empirical analysis and model study of personal credit scoring method based on discriminant analysis[J]. Journal of Dalian University of Technology:Social Sciences, 2009, 30 (1) : 6 –10. |
| [10] | 田方, 杨永发, 麻平社, 等. 逐步判别分析法在鄂尔多斯盆地油田的应用[J]. 国外测井技术, 2005, 20 (1) : 40 –43. |
| [11] |
王研, 张灵军, 严桂林, 等. 七参数判别法及其在松辽盆地东南隆起区油、气、水层判别中的应用[J].
中国海上油气:地质, 2002, 16 (1) : 62 –65.
Wang Yan, Zhang Lingjun, Yan Guilin, et al. A 7-parameter discrimination method and its application to identification of oil-, gas-and water bearing layers in the Southeast Uplift Area, Songliao Basin[J]. China Offshore Oil and Gas:Geology, 2002, 16 (1) : 62 –65. |
| [12] |
石豫川, 王哲, 万国荣, 等. 山区高等级公路边坡岩体分级研究[J].
岩石力学与工程学报, 2005, 24 (6) : 939 –944.
Shi Yuchuan, Wang Zhe, Wan Guorong, et al. Study of mountain highway slope mass rating[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24 (6) : 939 –944. |
| [13] | 田国华, 刘江, 韩波. 低孔渗储层油水层判别分析方法[J]. 黑龙江大学自然科学学报, 2004, 21 (1) : 35 –38. |
| [14] |
杨雪, 潘保芝, 张晓明, 等. 松辽盆地低孔低渗砂岩油气层的指标判别[J].
石油物探, 2009, 48 (1) : 57 –60.
Yang Xue, Pan Baozhi, Zhang Xiaoming, et al. Index identification of low porosity & permeability sandstone reservoir in Songliao Basin[J]. Geophysical Prospecting for Petroleum, 2009, 48 (1) : 57 –60. |
| [15] | 唐洪. 油层含油性判别分析[J]. 西南石油学院学报, 2004, 26 (1) : 13 –15. |
 2015, Vol. 37
2015, Vol. 37


