引 言

近年来，数值模拟已成为石油工业的必备技术手段。由于油田区域广阔，从地质模型生成的数据往往是海量的，超出数值模拟工具的处理范围。实际应用于油藏数值模拟的计算网格都是建立在较大尺度上的，因此，一个计算网格往往包含很多特性不同的子区域。为了给定相应大尺度网格上的特性参数，必须要对地质参数，特别是渗透率进行“粗化”处理。

目前已发展了很多参数粗化的方法，包括：试探性假定方法^[1]、重整化方法^[2-4]、均匀化理论^[5-6]、大尺度平均理论^[7-8]、统计分析方法^[9]等。在众多“粗化”方法中，直接数值求解非均匀多孔介质中的单相稳态渗流，可以在各种渗透率分布条件下得到相对可靠的“粗化”渗透率值，因而得到广泛应用^[10-11]。渗透率粗化的数值算法最早由Begg S H和Carter R R提出，他们在两侧边界加定压条件，另外两侧边界加绝流条件求解流场来实现粗化^[12]，但该方法只能得到对角化的等效渗透率。为克服该缺点，Durlofsky提出利用双周期边界条件求解流场，可以有效计算出完整的渗透率张量^[13]。在具体计算过程中使用传统的五点中心差分格式^[14]

$ \left\{ \begin{array}{l} {\left( {{Q_x}} \right)_{i + 1/2, j}} = - {{\overline K}_{i + 1/2, j}}\left( {{p_{i + 1, j}} - {p_{i, j}}} \right)/\Delta x\\ {\left( {{Q_y}} \right)_{i, j + 1/2}} = - {{\overline K}_{i, j + 1/2}}\left( {{p_{i, j + 1}} - {p_{i, j}}} \right)/\Delta y \end{array} \right. $

(1)

传统算法中，采用渗透率的调和平均值作为网格界面处的平均渗透率值。大量的研究表明，调和平均会导致计算出的平均渗透率值偏低。在某些极端情况下，计算值与真值间会存在数量级上的差别，从而使数值模拟失效^[15-16]。因而，在强非均匀多孔介质中，这些建立在传统差分格式上的渗透率粗化算法计算效率不高，要得到可靠的精度结果，需要进行足够细分，然而这是与参数粗化过程的初衷相违背的。所以，高精度的粗化算法必须建立在高精度的流场数值格式之上。Liu Z F和Wang X H在研究渗流方程问题时，利用有限分析法建立了一种高精度高效率的流场差分格式^[17]。该格式只需进行很少的细分就能得到流场的高精度数值解。所以，本文利用该有限分析方法，采用Durlofsky提出的双周期边界条件，从而得到高效的求解“粗化”渗透率的新算法。

1 控制方程及双周期边界条件

二维单相稳态渗流的控制方程为

$ \nabla \cdot \left( {K\nabla p} \right) = 0 $

(2)

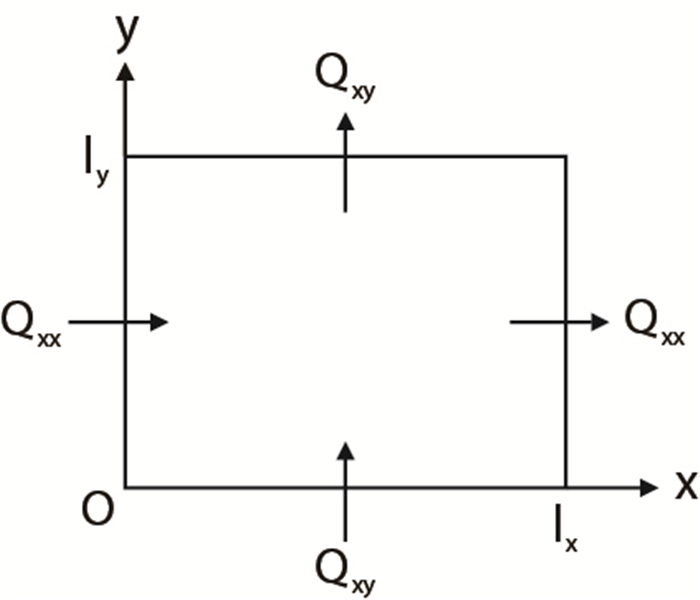
由于地质构造和地层特性的复杂分布导致渗透率等参数在空间分布上是不均匀的，在数值模拟的区域，渗透率会形成强的间断。体现在计算网格上，就是相邻计算网格的渗透率不同，且可能会存在很大的差异。求解方程(2)需要给出适定的边界条件，为有效求解出“粗化”渗透率的各分量，Durlofsky给出如下边界条件(图 1)

$ \left\{ {\begin{array}{*{20}{l}} {p\left( {{l_x}, y} \right) - p\left( {0, y} \right) = \Delta {p_x}}\\ {p\left( {x, {l_y}} \right) - p\left( {x, 0} \right) = 0}\\ {{\boldsymbol{u}}\left( {{l_x}, y} \right) = {\boldsymbol{u}}\left( {0, y} \right)}\\ {{\boldsymbol{u}}\left( {x, {l_y}} \right) = {\boldsymbol{u}}\left( {x, 0} \right)} \end{array}} \right. $

(3)

结合边界条件(3)，数值求解类拉普拉斯方程(2)，可求得等效渗透率的两个分量

$ \left\{ {\begin{array}{*{20}{l}} {{K_{xx}} = - \frac{{{Q_{xx}}/{l_y}}}{{\Delta {p_x}/{l_x}}}}\\ {{K_{xy}} = - \frac{{{Q_{xy}}/{l_x}}}{{\Delta {p_x}/{l_x}}}} \end{array}} \right. $

(4)

渗透率张量的另外两个分量$K_{yx}$与$K_{yy}$可以通过交换$x$和$y$方向上的边界条件，重新求解方程(2)得到。

2 求解控制方程的有限分析算法

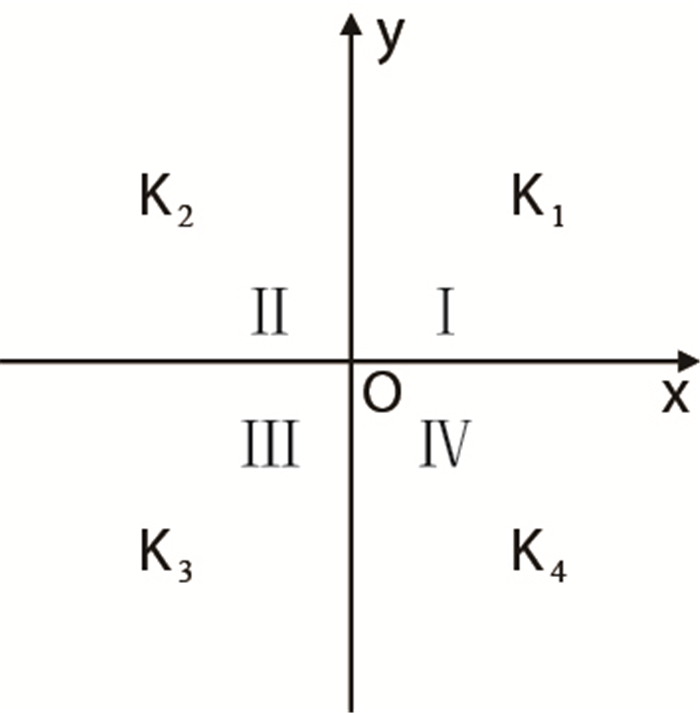
由于流量是连续的，因此渗透率的间断会导致压力梯度也相应发生间断。这一事实会造成在渗透率间断情况下数值求解相关方程的困难。假定压力在网格节点邻域(图 2)具有幂律分布，可推导出一个重要的解析解^[17]

(1)${K_1}{K_3} = {K_2}{K_4}$时

当${K_1}{K_3} = {K_2}{K_4}$时，各象限内的压力解为

$ \left\{ {\begin{array}{*{20}{l}} {{p_1} = {p_0} + {A_1}x + {B_1}y}\\[6pt] {{p_2} = {p_0} + \dfrac{{{K_1}}}{{{K_2}}}{A_1}x + {B_1}y}\\[6pt] {{p_3} = {p_0} + \dfrac{{{K_1}}}{{{K_3}}}{A_1}x + \dfrac{{{K_2}}}{{{K_3}}}{B_1}y}\\[6pt] {{p_4} = {p_0} + {A_1}x + \dfrac{{{K_1}}}{{{K_4}}}{B_1}y} \end{array}} \right. $

(5)

(2)${K_1}{K_3} \neq {K_2}{K_4}$时

当${K_1}{K_3} \neq {K_2}{K_4}$时，各象限内的压力解在极坐标下可表示为

$ \begin{equation} \left\{ {\begin{array}{*{20}{l}} {{p_1} = {A_1}{r^{1 - \alpha }}\cos \left[{\theta \left( {1-\alpha } \right)} \right] + {A_1}{r^{1 - \alpha }}C\sin \left[{\theta \left( {1-\alpha } \right)} \right] + {p_0}}\\[8pt] {{p_2} = {A_1}{r^{1 - \alpha }}\left( {\sin \dfrac{\pi }{2}\alpha + C\cos \dfrac{\pi }{2}\alpha } \right)\cos \left[{(\theta-\dfrac{\pi }{2})\left( {1-\alpha } \right)} \right]}\\[6pt] {\;\;\;\;\;\;\; - {A_1}{r^{1 - \alpha }}\dfrac{{K_1}}{{K_2}}\left( {\cos \dfrac{\pi }{2}\alpha - C\sin \dfrac{\pi }{2}\alpha } \right)\sin \left[{\left( {\theta-\dfrac{\pi }{2}} \right)\left( {1-\alpha } \right)} \right] + {p_0}}\\[8pt] {{p_3} = {A_1}{r^{1 - \alpha }}\left( {\sin \dfrac{\pi }{2}\alpha - \dfrac{{K_1}}{{K_4}}C\cos \dfrac{\pi }{2}\alpha } \right)\cos \left[{\left( {\theta + \dfrac{\pi }{2}} \right)\left( {1-\alpha } \right)} \right]}\\[6pt] {\;\;\;\;\;\; + {A_1}{r^{1 - \alpha }}\dfrac{{K_4}}{{K_3}}\left( {\cos \dfrac{\pi }{2}\alpha + \dfrac{{K_1}}{{K_4}}C\sin \dfrac{\pi }{2}\alpha } \right)\sin \left[{\left( {\theta + \dfrac{\pi }{2}} \right)\left( {1-\alpha } \right)} \right] + {p_0}}\\[8pt] {{p_4} = {A_1}{r^{1 - \alpha }}\cos [\theta \left( {1-\alpha } \right)] + {A_1}{r^{1 - \alpha }}\dfrac{{K_1}}{{K_4}}C\sin \left[{\theta \left( {1-\alpha } \right)} \right] + {p_0}} \end{array}} \right. %\sweqno \end{equation} $

(6)

$ \begin{equation} \alpha = \left| {\dfrac{2}{\pi }{\tan^{ - 1}}\left( {\dfrac{{{K_3}{K_1} - {K_2}{K_4}}}{{\sqrt {{K_1}{K_2}{K_3}{K_4}({K_1} + {K_2} + {K_3} + {K_4})(\dfrac{1}{{{K_1}}} + \dfrac{1}{{{K_2}}} + \dfrac{1}{{{K_3}}} + \dfrac{1}{{{K_4}}})} }}} \right)} \right| \end{equation} $

(7)

$ \begin{equation} C = {\rm{sgn}}\left (\dfrac{{{K_1}}}{{{K_2}}} - \dfrac{{{K_4}}}{{{K_3}}}\right )\sqrt {\dfrac{{{K_4}\left( {{K_1} + {K_2} + {K_3} + {K_4}} \right)}}{{{K_1}{K_2}{K_3}(\dfrac{1}{{{K_1}}} + \dfrac{1}{{{K_2}}} + \dfrac{1}{{{K_3}}} + \dfrac{1}{{{K_4}}})}}} \end{equation} $

(8)

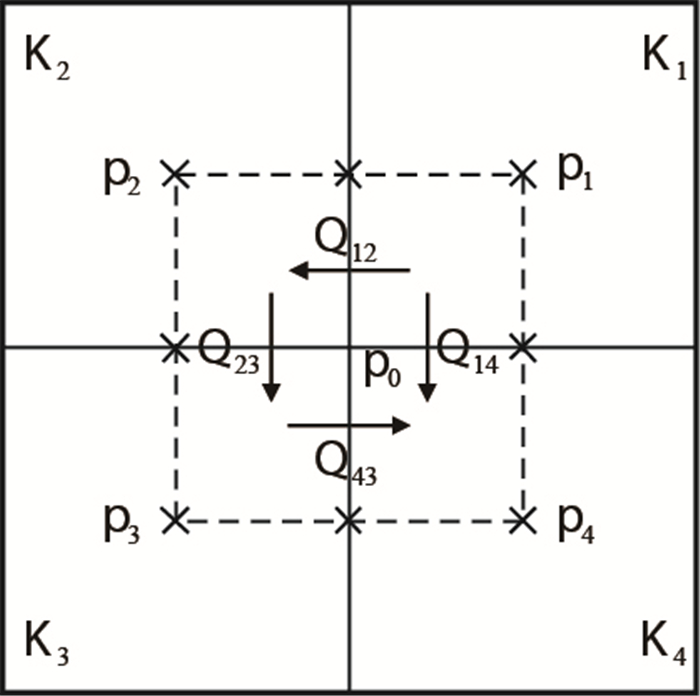
基于式(6)，可以构建相应的有限分析算法。图 3给出了典型的二维方网格系统的局部示意图。网格边长不妨设定为1。确定跨网格界面流量与网格节点压力以及各网格渗透率的关系，是数值算法的核心。

利用角域幂律解式(6)，可以得到跨界面流量计算表达式

$ \left\{ \begin{array}{l} {Q_{12}} = {\gamma _{12}}\left( {{p_1} - {p_2}} \right)\\ {Q_{23}} = {\gamma _{23}}\left( {{p_2} - {p_3}} \right)\\ {Q_{43}} = {\gamma _{43}}\left( {{p_4} - {p_3}} \right)\\ {Q_{14}} = {\gamma _{14}}\left( {{p_1} - {p_4}} \right) \end{array} \right. $

(9)

$ \left\{ \begin{array}{l} {\gamma _{12}} = \dfrac{{{\lambda _{Q, 12}}}}{{{\lambda _1} - {\lambda _2}}} \\[7pt] {\gamma _{23}} = \dfrac{{{\lambda _{Q, 23}}}}{{{\lambda _2} - {\lambda _3}}} \\[7pt] {\gamma _{43}} = \dfrac{{{\lambda _{Q, 43}}}}{{{\lambda _4} - {\lambda _3}}} \\[7pt] {\gamma _{14}} = \dfrac{{{\lambda _{Q, 14}}}}{{{\lambda _1} - {\lambda _4}}} %\\ \end{array} \right. $

(10)

$ {\lambda _2} \!=\!{\left( {\dfrac{{\sqrt 2 }}{2}} \right)^{1\! -\! \alpha }}\dfrac{{{K_1}}}{{{K_2}}}\left( {C\sin \dfrac{\pi }{2}\alpha \! -\! \cos \dfrac{\pi }{2}\alpha } \right)\sin \dfrac{\pi }{4}\left( {1 \!- \!\alpha } \right)+ \\ {\left( {\dfrac{{\sqrt 2 }}{2}} \right)^{1 \!\!- \alpha }}\left( {\sin \dfrac{\pi }{2}\alpha \!+\! C\cos \dfrac{\pi }{2}\alpha } \right)\cos \dfrac{\pi }{4}\left( {1\! -\! \alpha } \right) $

(11)

$ \begin{equation} {\lambda _1} = {\left( {\dfrac{{\sqrt 2 }}{2}} \right)^{1 - \alpha }}\left[{\cos \dfrac{\pi }{4}\left( {1-\alpha } \right) + C\sin \dfrac{\pi }{4}\left( {1-\alpha } \right)} \right] %\sweqno \end{equation} $

(12)

$ \begin{array}{l} {\lambda _3} = {\left( {\frac{{\sqrt 2 }}{2}} \right)^{1 - \alpha }}\cos \frac{\pi }{4}\left( {1 - \alpha } \right)\left( {\sin \frac{\pi }{2}\alpha - \frac{{{K_1}}}{{{K_4}}}C\cos \frac{\pi }{2}\alpha } \right) - \\ {\left( {\frac{{\sqrt 2 }}{2}} \right)^{1 - \alpha }}\frac{{{K_4}}}{{{K_3}}}\sin \frac{\pi }{4}\left( {1 - \alpha } \right)\left( {\cos \frac{\pi }{2}\alpha + \frac{{{K_1}}}{{{K_4}}}C\sin \frac{\pi }{2}\alpha } \right) \end{array} $

(13)

$ \begin{equation} {\lambda _4} = {\left( {\dfrac{{\sqrt 2 }}{2}} \right)^{1 - \alpha }}\left[{\cos \dfrac{\pi }{4}\left( {1-\alpha } \right)-\dfrac{{{K_1}}}{{{K_4}}}C\sin \dfrac{\pi }{4}\left( {1-\alpha } \right)} \right] \end{equation} $

(14)

$ {\lambda _{Q, 12}} = \dfrac{1}{{{2^{1 - \alpha }}}}\left (\cos \dfrac{\pi }{2}\alpha - C\sin \dfrac{\pi }{2}\alpha \right ){K_1} $

(15)

$ {\lambda _{Q, 23}} = \dfrac{1}{{{2^{2 - \alpha }}}}\sin \pi \alpha + C\left( {1 + \cos \pi \alpha } \right)\\ + \dfrac{1}{{{2^{2 - \alpha }}}}\dfrac{{{K_1}}}{{{K_2}}}\left[{\sin \pi \alpha-C\left( {1-\cos \pi \alpha } \right)} \right]{K_2} $

(16)

$ {\lambda _{Q, 43}} = \dfrac{1}{{{2^{1 - \alpha }}}}\left( {\cos \dfrac{\pi }{2}\alpha + \dfrac{{{K_1}}}{{{K_4}}}C\sin \dfrac{\pi }{2}\alpha } \right){K_4} $

(17)

$ {\lambda _{Q, 14}} = \dfrac{1}{{{2^{1 - \alpha }}}}C{K_1} $

(18)

以上有限分析算法结合双周期边界条件，就可以得到求解“粗化”渗透率的高效算法。

3 数值算例

考察大小为$L{\times}M$的方网格计算系统中的单相稳态渗流。边界条件为双周期边界条件。为便于比较，还给出了其他一些常用差分算法(调和平均、几何平均等)的计算结果。

3.1 算例1

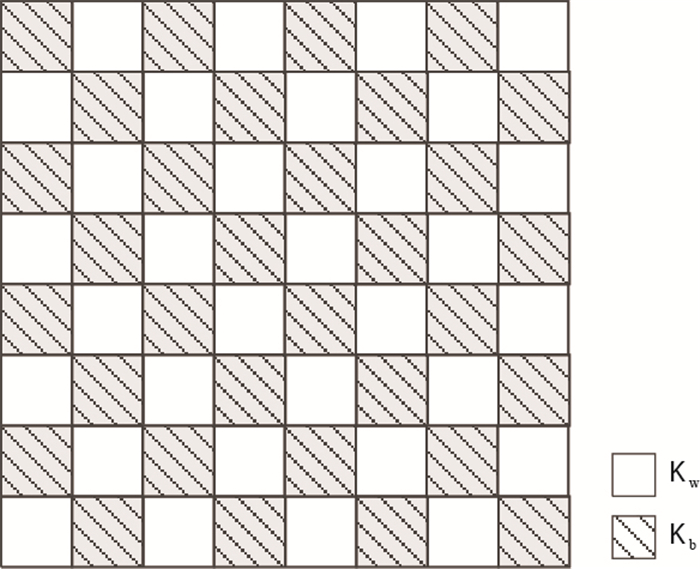
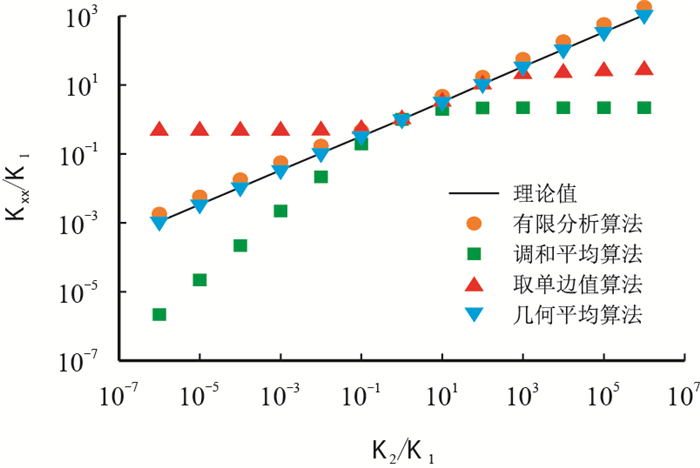
二维空间中具有棋盘型渗透率分布的算例常被用来检验相关理论分析和数值方法的有效性(图 4)。设黑白网格中的渗透率分别为$K_{\rm{b}}$、$K_{\rm{w}}$，则相应等效渗透率的准确值为$\sqrt {{K_{\rm{b}}}{K_{\rm{w}}}}$^[15]。图 5给出了对原始网格没有进行细分条件下各算法的计算结果。

有限分析算法的计算结果与理论值非常接近。虽然几何平均算法在本算例条件下也能得到很好的结果，但对其他条件，其结果可能变差。

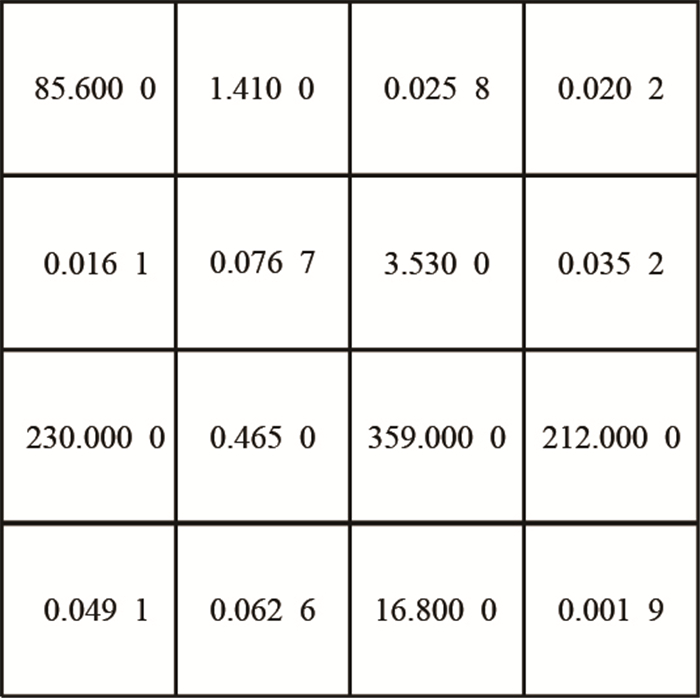
3.2 算例2

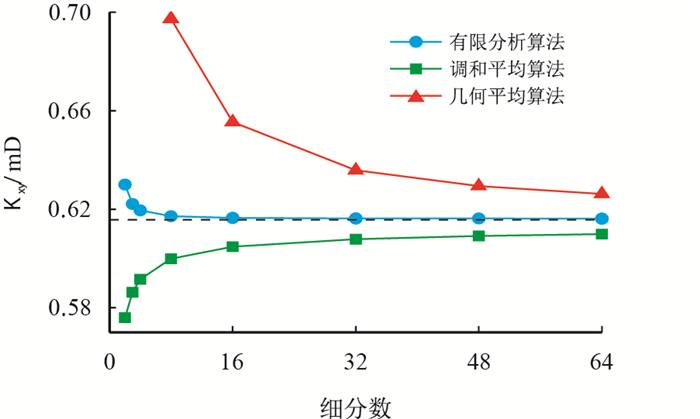
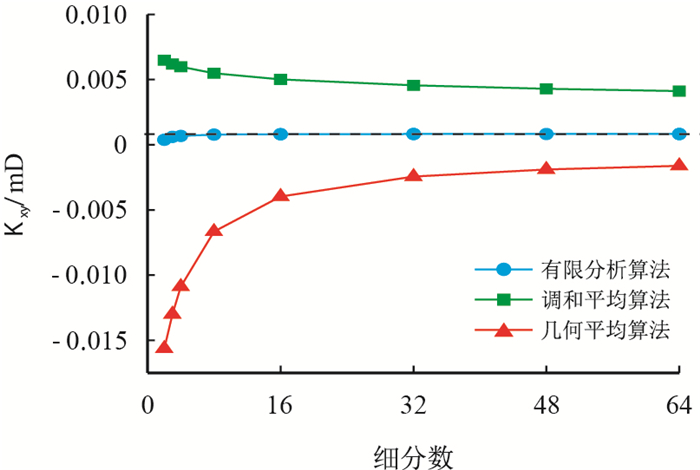
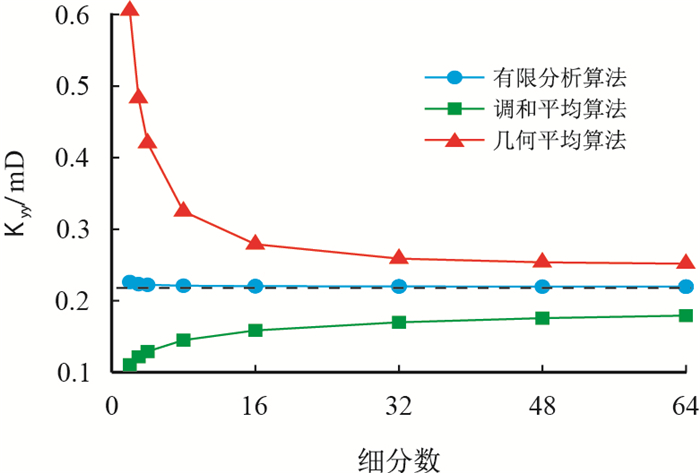
给出了二维空间中大小为4×4具有随机渗透率分布的网格系统，渗透率分布如图 6所示。图 7~图 9给出了各种算法所得的3个等效渗透率分量($K_{xx}$，$K_{xy}$，$K_{yy}$) 计算结果对细分数的收敛情况。

结果表明，有限分析法对3个分量的计算结果都能很快地收敛，一般情况下只需将原始网格细分至2×2或者3×3的计算网格就已经能得到非常精确的等效渗透率值，而调和平均算法则始终收敛很慢；几何平均算法虽然在棋盘式分布中能得到正确结果，但对其他随机分布的渗透率情况，其收敛速度也将变得很缓慢。

4 结 语

基于有限分析算法，提出了一种求解非均匀多孔介质“粗化”渗透率的数值方法，该方法适用于由线性Darcy定律描述的渗流流场。该算法沿用了Durlofsky提出的双周期边界条件，因而可以计算出完整的渗透率张量，同时又具有很高的计算效率。经过多个数值算例的检验，新算法在粗网格条件下(2×2或3×3的计算网格)，就可以获得相当高的精度。

由于本文中所利用的有限分析算法是基于线性Darcy定律的，因而对于特低渗透等非Darcy渗流并不适用。如何建立相关非Darcy渗流的有限分析数值算法，是未来一项很有挑战性的工作。

符号说明

$Q$——流量，m³/s；

$\overline K$——平均渗透率，mD；

$p$——压力，Pa；

$\Delta x$——横向步长，m；

$\Delta y$——纵向步长，m；

$l$——区域边长，m；

$x$——横坐标，m；

$y$——纵坐标，m；

$\Delta p$——压差，Pa；

$\boldsymbol{u}$——速度，m/s；

$K$——渗透率，mD；

$p_0$——网格节点压力，Pa；

$K_1，K_2，K_3，K_4$——第1、2、3、4象限的渗透率，mD；

$r$——极坐标的极径，m；

$\theta$——极坐标的极角，(°)；

$p_1，p_2，p_3，p_4$——第1、2、3、4象限的压力，Pa；

$A_1，B_1$——系数，无因次；

$Q_{12}，Q_{23}，Q_{43}，Q_{14}$——界面1到界面2的流量，界面2到界面3的流量，界面4到界面3的流量，界面1到界面4的流量，m³/s；

$L$——横向网格数；

$M$——纵向网格数；

下标$x，y$——$x$向，$y$向；

下标$i，j$——$x$向第$i$个网格，$y$向第$j$个网格。