2. 美国科罗拉多矿业大学石油工程系, 科罗拉多 高登 80401;
3. 中国地质大学(北京)能源学院, 北京 海淀 100083
2. Department of Petroleum Engineering, Colorado School of Mines, Golden, Colorado 80401, USA;
3. School of Energy Resources, China University of Geosciences(Beijing), Haidian, Beijing 100083, China
目前,中国二氧化碳排放量居世界第二位,并仍在快速增长,预计到2025年前后,中国的二氧化碳排放总量会超过美国,居世界第一位。另一方面,中国石油供求矛盾日益突出,2010年以后进口依赖度始终约在50%以上。中国大陆东部地区老油气田开采区是封闭条件非常好的地下储气库,向油层中注入二氧化碳可以实现温室气体的长期埋存,同时还能大幅度提高原油的采收率[1-2]。数值模拟是油藏二氧化碳驱项目方案设计、预测和管理的主要技术手段。由于混相驱或非混相驱过程中二氧化碳同原油和地下水的复杂相互作用,常用的黑油模型已不适用,必须采用组分模型进行计算分析。
本文的目的是建立裂缝性油藏二氧化碳驱的多相多组分数值计算模型,给出相关的计算方法和主要公式;这一计算模型主要包括裂缝性油藏二氧化碳驱多相多组分的基本控制方程、二氧化碳的吸附及原油重组分的沉淀、多组分气相和油相物性的计算、沥青质沉积对渗透率的影响、油-水-气(二氧化碳)三相地下条件下的相平衡计算方法等。
裂缝性油藏数值模拟最常采用的理论是双孔隙度-单渗透率、双孔隙度-双渗透率等双重介质模型[3-5]。从双重介质的概念出发,很多学者都提出了相应的三重介质模型,其中,基于多重相关连续介质的多重介质模型灵活有效、适用性广[6-8],本文以此多重介质模型为基础,研究裂缝性油藏数值模拟的组分模型。
多相多组分流体在地下条件下的相平衡计算是组分模型的核心问题之一,主要有平衡常数法、基于Rachford-Rice函数的闪蒸计算法和Gibbs自由能最小化法3种计算方法。本文分别给出了采用这3种方法计算油-水-气(二氧化碳)三相流体相平衡的主要计算公式,并简要分析了这3种相平衡计算方法的优缺点。
1 基本控制方程注入的二氧化碳在油藏条件下通常呈超临界状态(以下简称为气相)。假设二氧化碳驱过程中等温、不发生化学反应、且孔隙中相平衡能够瞬时完成,则多相多组分流体的流动由质量守恒定律来控制。
1.1 质量守恒方程裂缝性油藏可用裂缝-基质的双重介质理论来描述,裂缝和基质同为储集空间,裂缝为主要的流动通道。根据文献[6-8]的多重介质理论,双重介质中裂缝间的流动、基质间的流动、裂缝-基质间的多相流动,都可抽象地归纳为单元间的流动,从而采用统一的质量守恒表达式。同时,这一理论还能够考虑不同的裂缝分布模式,如图 1所示的裂缝分布,可以抽象为图 2所示的概念模型,并根据此概念模型确定裂缝系统和基质系统间的窜流系数。其他的分布模式可参考文献[8]。
 |
| 图1 裂缝性储层的一种裂缝分布 Fig. 1 A fracture pattern of fractured formation |
 |
| 图2 裂缝分布对应的概念模型 Fig. 2 Conceptual model of the fracture pattern |
本文考虑的流体包括气相(二氧化碳)、水相和油相,每相流体都包含有若干质量组分。多孔介质中单元n中组分κ的质量守恒方程为
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\int\limits_{{V_n}} {{M^\kappa }} {\rm{d}}{V_n} = \int\limits_{{\mathit{\Gamma} _n}} {{{\vec F}^\kappa } \cdot \vec n} {\rm{d}}{\mathit{\Gamma} _n} + \int\limits_{{V_n}} {{q^\kappa }} {\rm{d}}{V_n} $ | (1) |
孔隙介质中各相流体组分κ的质量累积为
| $ {M^\kappa } = \phi \sum\limits_\beta {{S_\beta }} {\rho _\beta }x_\beta ^\kappa + M_{{\rm{ads}}}^\kappa $ | (2) |
多孔介质中多相流动用扩展的Darcy定律来描述,组分κ因渗流引起的质量传输项为
| $ {{\vec F}^\kappa }{{\rm{|}}_{{\rm{adv}}}} = \sum\limits_\beta {x_\beta ^\kappa {{\vec F}_\beta }} $ | (3) |
| $ {{\vec F}_\beta } = {\rho _\beta }{{\vec u}_\beta } = - K\frac{{{K_{{\rm{r}}\beta }}{\rho _\beta }}}{{{\mu _\beta }}}\left( {\nabla {p_\beta } - {\rho _\beta }{\rm{\tilde g}}} \right) $ | (4) |
组分κ(如二氧化碳等)在多孔介质中的扩散采用扩展的Fick定律来描述,相β中组分κ因扩散引起的质量传输项为
| $ {\left. {F_\beta ^\kappa } \right|_{{\rm{dis}}}} =-\phi {\rho _\beta }{\rm{D}}_\beta ^\kappa \nabla x_\beta ^\kappa $ | (5) |
二氧化碳在岩石或黏土固体颗粒上的吸附是一个动态的过程,假设吸附完成的速度相对于油藏中其他物理过程来说足够快,则这一吸附过程可用瞬时、可逆、等温吸附来描述
| $ M_{{\rm{ads}}}^\kappa = (1-\phi ){\rho _{\rm{s}}}K_{{\rm{d}}, \beta }^\kappa {\rho _\beta }x_\beta ^\kappa $ | (6) |
二氧化碳注入后,原油中重组分的沉淀会对储层渗透性能造成严重影响。重组分的沉淀会阻塞孔隙喉道、降低渗透率,并可能会使岩石的湿润性由亲水转变为亲油。为了考虑这种情况并避免进行复杂的四相混合物相平衡计算,本文假设重组分的沉淀可用式(6)的等温吸附来描述,采用非线性的Langmuir等温吸附时,吸附平衡系数Kd, βκ是相β中二氧化碳摩尔分数的函数,可由试验来确定。
2 本构关系和流体的物性本构关系用来确定多相多组分流体流动各个物理过程中的变量和参数之间的内在关系和约束。根据本构关系,可由主变量来计算各相流体的物理性质。
2.1 本构关系多相多组分流动体系中,各相流体饱和度及各组分的摩尔分数应当满足如下的约束方程
| $ \sum\limits_\beta {{{\rm{S}}_\beta }} = 1 $ | (7) |
| $ \sum\limits_\kappa {x_\beta ^\kappa } = 1 $ | (8) |
气-水-油的三相体系中,毛细管力由流相的饱和度来确定。如果选择气相为参考相,则水相和油相的压力计算公式为
| $ {p_{\rm{w}}} = {p_{\rm{g}}}-{p_{{\rm{cgw}}}}\left( {{S_{\rm{w}}}, {\mkern 1mu} {S_{\rm{g}}}} \right) $ | (9) |
| $ {p_{\rm{o}}} = {p_{\rm{g}}}-{P_{{\rm{cgo}}}}\left( {{S_{\rm{w}}}, {\mkern 1mu} {S_{\rm{o}}}} \right) $ | (10) |
气水毛细管力pcgw和气油毛细管力pcgo是水相饱和度Sw和油相饱和度So的函数。油水毛细管力的计算公式为
| $ {p_{{\rm{cow}}}} = {p_{{\rm{cgw}}}}-{p_{{\rm{cgo}}}} = {p_{\rm{o}}}-{p_{\rm{w}}} $ | (11) |
气-水-油三相体系的三相相对渗透率对于准确预测多相流体流动动态十分重要。以往的数值计算模型中,通常基于这样的假定:气相为完全非润湿相,三相体系中一液相为完全的润湿相,另一液相介于二者之间为中间润湿相;用完全非润湿相和完全润湿相的两相相对渗透率作为它们各自的三相相对渗透率,中间润湿相的三相相对渗透率则由一些简单模型计算而得,如Stone Ⅱ方法等[9-11]。
然而,Dria D E和Pope G A的研究结果表明[12],对于二氧化碳驱条件下的气-水-油三相体系,各相的三相相对渗透率并不是上述计算方法中依赖于两相的饱和度,而是仅与该相的饱和度有关。据此,相β的三相相对渗透率可表示为该相饱和度的函数
| $ {K_{{\rm{r}}{\kern 1pt} \beta }} = {\mkern 1mu} {\mkern 1mu} {K_{{\rm{r}}{\kern 1pt} \beta }}\left( {{S_\beta }} \right) $ | (12) |
2.2各相流体的物性
二氧化碳组分在不同温度和压力下的密度采用文献[13]给出的关系式,不同温度和压力下的黏度可采用文献[14]中的数据。气相的主要组分为二氧化碳和天然气中烃类气体。气相的PVT性质,采用Soave-Redlich-Kwong (SRK)状态方程来描述[15-16]。纯组分的SRK状态方程为
| $ {Z^3}- {Z^2} + \left[{{A^*}-{B^*}-{{({B^*})}^2}} \right]Z -{A^*}{B^*} = 0 $ | (13) |
其中,
| $ a = {\left\{ {1 + \left( {0.48 + 1.574\omega- 0.176{\omega ^2}} \right)\left[{1-{{\left( {T/{T_c}} \right)}^{1/2}}} \right]} \right\}^2} \cdot \frac{{0.42748{{\rm{R}}^2}{T_{\rm{c}}}^2}}{{{p_{\rm{c}}}}} $ | (14) |
| $ b = \frac{{0.08664{\rm{R}}{T_{\rm{c}}}}}{{{p_{\rm{c}}}}} $ | (15) |
对于多组分的气相,则可采用文献[17]提出的混合规则进行计算,混合物的a、b系数设为am和bm,可以由纯组分的参数求得,设纯组分κ的a和b系数分别是aκ和bκ,则计算公式为
| $ {a_{\rm{m}}} = {\left( {\sum\limits_\kappa {x_{\rm{g}}^\kappa \sqrt {{a_\kappa }} } } \right)^2} $ | (16) |
| $ {b_{\rm{m}}} = \sum\limits_\kappa {x_{\rm{g}}^\kappa } {b_\kappa } $ | (17) |
根据式(13)得到气相的压缩因子后,其摩尔密度为
| $ {\rho _{\rm{g}}} = p{\rm{R}}TZ $ | (18) |
纯组分κ的黏度μκ是压力和温度的函数。根据Chapman-Enskog动力学理论,气相的动力黏度μg可由纯组分的动力黏度μκ和组成表述
| $ {\mu _{\rm{g}}} = \sum\limits_{\kappa = 1}^N {\frac{{{x_{\rm{g}}}^\kappa {\mu _\kappa }}}{{\sum\nolimits_{\lambda = 1}^N {{x_{\rm{g}}}^\lambda {\mathit{\Phi} _{\kappa \lambda }}} }}} $ | (19) |
Φκλ是二元相互作用参数,表述为
| $ {\mathit{\Phi} _{\kappa \lambda }} = \frac{{{{\left[ {1 + {{\left( {{\mu _\kappa }/{\mu _\kappa }/{\mu _\lambda }} \right)}^{1/2}}{{\left( {{M_\lambda }/{M_\lambda }} \right)}^{1/4}}} \right]}^2}}}{{{{\left[ {8\left( {1 + {M_\kappa }/{M_\lambda }} \right)} \right]}^{1/2}}}} $ | (20) |
对于油相,摩尔密度的计算公式为
| $ {\rho _{\rm{o}}} = p{\rm{R}}T{Z_{\rm{o}}} $ | (21) |
压缩因子Zo根据原油的组成成分按照式(13)计算。
原油纯组分的黏度计算公式为
| $ \ln \mu = A'-\frac{{B'}}{T} + C'T + D'{T^2} $ | (22) |
油相的黏度可由其组成按照式(23)计算
| $ {\mu _{\rm{o}}} = \prod\limits_{\kappa = 1}^{{N_{\rm{c}}}} {{\mu _\kappa }^{x_{\rm{o}}^\kappa }} $ | (23) |
对于水的摩尔密度和黏度,则根据文献[18]的关系式和数据来确定。由于水相中二氧化碳和烃类溶解度相对较小,因此假定溶解于水的二氧化碳和烃类对水相本身的摩尔密度和黏度影响不大。
2.3 沥青质沉积对渗透率的影响沥青质沉积导致的渗透率降低不仅取决于孔隙减少量,还取决于孔隙结构和沉积物质在孔隙中的分布。如图 3所示[19],可采用文献[19]的管串联模型,将孔隙结构考虑为由孔隙和喉道串联构成的毛管,R是孔隙的半径,r是喉道的半径,沥青质在串联毛管内壁均匀沉积,渗透率主要由喉道控制。
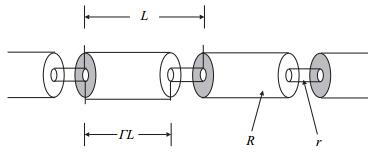 |
| 图3 串状毛管模型 Fig. 3 Tubes-in-series model |
考虑沥青质沉积后的渗透率按式(24)式(26)计算
| $ \frac{K}{{{K_0}}} = {\theta ^2}\frac{{1- {\rm{ }}\mathit{\Gamma} + {\rm{ }}\mathit{\Gamma} /{w^2}}}{{1- \mathit{\Gamma} + \mathit{\Gamma} {{\left[{\theta /\left( {\theta + w-1} \right)} \right]}^2}}} $ | (24) |
| $ \theta = \frac{{1-{S_{\rm{s}}}-{\phi _r}}}{{1-{\phi _r}}} $ | (25) |
| $ w = 1 + \frac{{1/\mathit{\Gamma} }}{{1/{\phi _r}-1}} $ | (26) |
无论是混相二氧化碳驱油还是非混相二氧化碳驱油,其形成过程都是随着油层温度、压力和原油组成的变化而产生的相态平衡变化过程。加滕完司[20]对细管二氧化碳驱油的研究表明:在温度、相对渗透率和黏度相同、压力相差不是很大的(10.3 MPa和12.4 MPa)的情况下,二氧化碳同原油的相平衡特性有着十分显著的差异;原油组分的不同,二氧化碳平衡常数变化明显。可见,准确的相平衡计算对于油藏二氧化碳驱的数值模拟至关重要。已有的一些组分模型数值计算方法需要在相平衡计算方面进行改进[21-25]。多相多组分流体在地下条件下的相平衡计算主要有平衡常数法、基于Rachford-Rice函数的闪蒸计算法和Gibbs自由能最小化法3种计算方法。
3.1 平衡常数法对于多组分体系内的相α和相β,组分κ的平衡常数定义为
| $ K_{\alpha \beta }^\kappa = \frac{{x_\alpha ^\kappa }}{{x_\beta ^\kappa }} $ | (27) |
这一平衡常数应该是多组分混合物温度、压力和组成的函数。对于烃类体系,文献[26]根据试验建议了关系式近似计算气-油平衡常数
| $ K_{{\rm{go}}}^i = \left( {\frac{{{p_{{\rm{c}}, i}}}}{p}} \right)\exp \left[{5.373\left( {1 + {\omega _i}} \right)\left( {1-\frac{{{T_{{\rm{c}}, i}}}}{T}} \right)} \right] $ | (28) |
在此基础上,Almehaideb R A等[27]根据大量的试验结果,建议了一个适用于高压体系的平衡常数计算公式
| $ K_{{\rm{go}}}^i = {\left( {\frac{{{p_{{\rm{c}}, i}}}}{{{p_{\rm{k}}}}}} \right)^{A-1}}\left( {\frac{{{p_{{\rm{c}}, i}}}}{p}} \right)\exp \left( {AK_i^*} \right) $ | (29) |
其中:
文献[28]基于多重介质模型,采用平衡常数法研究了二氧化碳驱多相多组分数值模拟方法,并编制了相应的计算程序。
平衡常数法采用基于试验的经验公式来计算平衡常数,能够避免复杂、耗时的相平衡计算,计算速度快、稳定性良好,但由于缺乏严密的热力学理论基础,难以很好地考虑原油不同组成的影响,计算结果可能同真实相平衡状态有一定的偏差。
3.2 基于Rachford-Rice函数的闪蒸计算法以气油两相体系为例,基于Rachford-Rice方法[29]的闪蒸计算的迭代步骤如下
(1) 估计组分i初始的油气平衡常数Kgoi和气相的摩尔分数nv;
(2) 按照式(30)~式(32)计算Rachford-Rice函数和新的气相摩尔分数(nv)new;
| $ f\left( {{n_{\rm{v}}}} \right) = \sum {\frac{{{z_i}\left( {K_{{\rm{go}}}^i-1} \right)}}{{1 + \left( {K_{{\rm{go}}}^i-1} \right){n_{\rm{v}}}}}} $ | (30) |
| $ f'\left( {{n_{\rm{v}}}} \right) =- \sum {\frac{{{z_i}{{\left( {K_{{\rm{go}}}^i- 1} \right)}^2}}}{{{{\left[{1 + \left( {K_{{\rm{go}}}^i-1} \right){n_{\rm{v}}}} \right]}^2}}}} $ | (31) |
| $ {\left( {{n_{\rm{v}}}} \right)_{{\rm{new}}}} = {n_{\rm{v}}}-\frac{{f\left( {{n_{\rm{v}}}} \right)}}{{f'\left( {{n_{\rm{v}}}} \right)}} $ | (32) |
(3) 迭代计算至nv同(nv)new的误差满足允许的要求;
(4) 计算组分i在气相中的摩尔分数yi和油相中的摩尔分数xi;
| $ {x_i} = \frac{{{z_i}}}{{1-{n_{\rm{v}}} + {n_{\rm{v}}}K_{{\rm{go}}}^i}} $ | (33) |
| $ {y_i} = \frac{{{z_i}K_{{\rm{go}}}^i}}{{1-{n_{\rm{v}}} + {n_{\rm{v}}}K_{{\rm{go}}}^i}} $ | (34) |
(5) 根据气相和油相的摩尔组成分别计算气相中组分i的逸度系数φgi和油相中组分i的逸度系数φoi;
(6) 计算新的油气平衡常数,返回步骤1进行迭代,直至新的平衡常数满足误差要求。
| $ K_{{\rm{go}}}^i = \frac{{\varphi _{\rm{o}}^{\rm{i}}}}{{\varphi _{\rm{g}}^i}} $ | (35) |
上述闪蒸计算方法同基于经验公式的平衡常数法相比较,有较高的精度,但是因为需要反复迭代,因此计算量较平衡常数法大。组分模拟迭代求解过程中,当式(30)右项分母接近于零时,则该算法出现不收敛的情况。此外,基于Rachford-Rice函数的闪蒸计算法主要用于两相体系的相平衡计算,适用于三相体系相应的算法还有待研究和完善[30]。
3.3 Gibbs自由能最小化法根据多相体系相平衡的热力学理论,多组分混合物处于稳定状态时应满足Gibbs自由能最小的条件。油-水-气三相体系总的Gibbs自由能为
| $ {n^{\rm{T}}}G = \sum\limits_i {{n^i}G_0^i} + {\rm{R}}T\sum\limits_\beta {\sum\limits_i {\left[{{n^{\rm{T}}}L_\beta ^{}x_\beta ^i\ln \left( {\varphi _\beta ^ix_\beta ^ip} \right)} \right]} } $ | (36) |
相β中组分i的逸度系数可由状态方程及式(37)计算得到
| $ \ln \varphi _\beta ^i = {\left\{ {\frac{1}{{{\rm{R}}T}}\int_V^\infty {\left[{{{\left( {\frac{{\partial P}}{{\partial {n^j}}}} \right)}_{T, V, {n^{j \ne i}}}}-\frac{{{\rm{R}}T}}{V}} \right]} {\rm{d}}V -\ln Z} \right\}_\beta } $ | (37) |
由于体系达到相平衡时,体系的摩尔Gibbs自由能应达到最小,因此,油-水-气三相的平衡可通过搜索式(36)中摩尔Gibbs自由能最小值来进行。Gibbs自由能最小化方法理论严密、适应性广、计算稳定、收敛性好,比较适合于多相平衡计算,但是计算量比基于Rachford-Rice函数的闪蒸计算法要大。
4 数值解法对于式(1)的质量守恒方程,采用文献[6],文献[7]和文献[28]中的积分差分法进行空间离散、采用一阶向后差分进行时间离散,可写成残差形式
| $ R_n^{\kappa, t + \Delta t} = M_n^{\kappa, t + \Delta t}-M_n^{\kappa, t}-\frac{{\Delta t}}{{{V_n}}}\left\{ {\sum\limits_m {{A_{nm}}F_{nm}^{\kappa, t + \Delta t}} + {V_n}q_n^{\kappa, t + \Delta t}} \right\} = 0 $ | (38) |
可采用Newton-Raphson迭代法对方程(38)进行求解。
5 结语裂缝性油藏二氧化碳驱的多相多组分数值计算方法主要涉及如下问题的计算模拟:裂缝性油藏的多重介质模型、多相流动及多组分的扩散、二氧化碳在岩石固体骨架上的吸附、原油重组分的沉淀、储层条件下不同组分流体物性的计算方法、沥青质沉积对渗透率的影响、多相多组分的相平衡计算方法和数值离散方法。
本文研究了裂缝性油藏二氧化碳驱的油-水-气(二氧化碳)三相、多组分的数值计算模型,较为全面地给出了上述相关问题的计算方法和主要公式。对于裂缝性油藏可采用文献[6-8]和[28]的多重介质理论来描述,以便考虑不同的裂缝分布模式。裂缝系统内、基质系统内、裂缝-基质之间的多相流动,采用扩展的Darcy定律来描述。二氧化碳在油相中的扩散可采用Fick定律来描述。采用非线性的等温吸附来描述二氧化碳在岩石颗粒上的吸附及油相中沥青质在岩石骨架上的沉淀。沥青质沉积阻塞孔道对储层绝对渗透率的影响,采用串状毛管模型来考虑。各组分的质量守恒方程采用积分差分法进行空间离散,可采用全隐式格式通过Newton迭代法进行求解。
相平衡是二氧化碳驱组分模型的核心问题之一。不同压力及组成下二氧化碳同原油相平衡特性的差异十分显著,准确的相平衡计算对于油藏二氧化碳驱的数值模拟至关重要。对于油-水-气(二氧化碳)三相的相平衡计算,分别给出了平衡常数法、基于Rachford-Rice函数的闪蒸计算法和Gibbs自由能最小化法的计算方法,并简述了3种方法各自的优点和不足。
| [1] |
沈平平, 杨永智. 温室气体在石油开采中资源化利用的科学问题[J].
中国基础科学, 2006, 8 (3) : 23 –31.
Shen Pingping, Yang Yongzhi. Problems on enhanced oil recovery by using greenhouse gas[J]. China Basic Science, 2006, 8 (3) : 23 –31. |
| [2] |
沈平平, 黄磊. 二氧化碳-原油多相多组分渗流机理研究[J].
石油学报, 2009, 30 (2) : 247 –251.
Shen Pingping, Huang Lei. Flow mechanisms of multiphase multi-component CO2-crude oil system in porous media[J]. Acta Petrolei Sinica, 2009, 30 (2) : 247 –251. |
| [3] | Barenblatt G I, Zheltov I P, Kochina I N. Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks strata[J]. Journal of Applied Mathematics and Mechanics, 1960, 24 (5) : 1286 –1303. DOI:10.1016/0021-8928(60)90107-6 |
| [4] | Warren J E, Root P J. The behavior of naturally fractured reservoirs[J]. Society of Petroleum Engineers Journal, 1963, 3 (3) : 245 –255. DOI:10.2118/426-PA |
| [5] | Kazemi H. Pressure transient analysis of naturally fractured reservoirs with uniform fracture distribution[J]. Society of Petroleum Engineers Journal, 1969, 9 (4) : 451 –462. DOI:10.2118/2156-A |
| [6] | Pruess K. A practical method for modeling fluid and heat flow in fractured porous media[J]. Society of Petroleum Engineers Journal, 1985, 25 (1) : 14 –26. DOI:10.2118/10509-PA |
| [7] | Wu Y S, Pruess K. A Multiple-porosity method for simulation of naturally fractured petroleum reservoirs[J]. SPE Reservoir Engineering, 1988, 3 (1) : 327 –336. DOI:10.2118/15129-PA |
| [8] | Wu Y S, Di Y, Kang Z, et al. A multiple-continuum model for simulating single-phase and multiphase flow in naturally fractured vuggy reservoirs[J]. Journal of Petroleum Science and Engineering, 2011, 78 (1) : 13 –22. DOI:10.1016/j.petrol.2011.05.004 |
| [9] | Aziz K, Settari A. Petroleum reservoir simulation[M]. London: Chapman & Hall, 1979 . |
| [10] | Honarpour M M, Koederitz F, Herbert A. Relative permeability of petroleum reservoirs[M]. Florida: CRC Press, Inc., 1986 . |
| [11] | Kaluarachchi J J, Parker J C. An efficient finite element method for modeling multiphase flow[J]. Water Resources Research, 1989, 25 (1) : 43 –54. DOI:10.1029/WR025i001p00043 |
| [12] | Dria D E, Pope G A, Sepehrnoori K. Three-phase gas/oil/brine relative permeabilities measured under CO2 flooding conditions[C]. SPE 20184, 1993. |
| [13] | Hendriks C A, Blok K. Underground storage of carbon dioxide[J]. Energy Conversion and Management, 1993, 34 (9) : 949 –957. |
| [14] | Goodrich J H. Review and analysis of past and ongoing carbon dioxide injection field test[C]. SPE 8832, 1980. |
| [15] | Redlich O, Kwong J N S. On the thermodynamics of solutions. V. An equation of state. Fugacities of gaseous solutions[J]. Chemical Reviews, 1949, 44 (1) : 233 –244. DOI:10.1021/cr60137a013 |
| [16] | Soave G. Equilibrium constants from a modified RedlichKwong equation of state[J]. Chemical Engineering Science, 1972, 27 (6) : 1197 –1203. DOI:10.1016/0009-2509(72)80096-4 |
| [17] | Poling B E, Prausnitz J M, O'connell J P. The properties of gases and liquids[M]. New York: McGraw-Hill, 2001 . |
| [18] | International Formulation Committee. A formulation of the thermodynamic properties of ordinary water substance[R]. IFC Secretariat, Düsseldorf, Germany, 1967. |
| [19] | Verma A, Pruess K. Thermohydrological conditions and silica redistribution near high-level nuclear wastes emplaced in saturated geological formations[J]. Journal of Geophysical Research:Solid Earth(1978-2012), 1988, 93 (B2) : 1159 –1173. DOI:10.1029/JB093iB02p01159 |
| [20] | 加滕完司. CO2驱油中油藏流体的组份变化[J].刘倩, 译.采油工艺情报, 1989(2):83-91. |
| [21] |
叶继根, 吴向红. 油气藏三维三相组分模型软件研制与应用[J].
计算物理, 2000, 17 (5) : 548 –552.
Ye Jigen, Wu Xianghong. Software development and application of compositional model with three phase and 3D for oil/gas reservoir[J]. Chinese Journal of Computational, 2000, 17 (5) : 548 –552. |
| [22] |
张茂林, 喻高明, 梅海燕. 凝析油气藏拟组分数值模拟方法[J].
西南石油学院学报, 1991, 13 (2) : 38 –46.
Zhang Maolin, Yu Gaoming, Mei Haiyan. A method of pseudo-component numerical simulation for condensate oil-gas reservoir[J]. Journal of Southwest Petroleum Institute, 1991, 13 (2) : 38 –46. |
| [23] |
张茂林, 孙良田, 李士伦. 凝析油气藏K值多组分模型数值模拟方法[J].
石油学报, 1991, 12 (1) : 60 –68.
Zhang Maolin, Sun Liangtian, Li Shilun. A K-value compositional model for a retrograde condensate reservoir[J]. Acta Petrolei Sinica, 1991, 12 (1) : 60 –68. |
| [24] |
张烈辉, 张红梅, 鲁友常, 等. 模拟混相驱动态的拟四组分模型[J].
西南石油学院学报, 1999, 21 (4) : 64 –66.
Zhang Liehui, Zhang Hongmei, Lu Youchang, et al. Psedocompositional model for miscible flooding[J]. Journal of Southwest Petroleum Institute, 1999, 21 (4) : 64 –66. |
| [25] |
郎兆新, 程林松. 拟三维全组分模型[J].
石油大学学报:自然科学版, 1990, 14 (1) : 16 –25.
Long Zhaoxin, Cheng Linsong. A pseudo-three dimensional compositional model[J]. Journal of the University of Petroleum, China, 1990, 14 (1) : 16 –25. |
| [26] | Wilson G. A modified Redlich-Kwong equation of state applicable to general physical data calculations[C]. The 65th AICHE National meeting, Cleveland, 1969. |
| [27] | Almehaideb R A, Ashour I, El-Fattah K A. Improved K-value correlation for UAE crude oil components at high pressures using PVT laboratory data[J]. Fuel, 2003, 82 (9) : 1057 –1065. DOI:10.1016/S0016-2361(03)00004-8 |
| [28] | Di Y, Wu Y S, Ju B, et al. A practical compositional method for simulation of CO2 flooding in porous and fractured petroleum reservoirs[C]. SPE 145096, 2011. |
| [29] | Rachford Jr H H, Rice J D. Procedure for use of electronic digital computers in calculating flash vaporization hydrocarbon equilibrium[J]. Journal of Petroleum Technology, 1952, 4 (10) : 19 –3. DOI:10.2118/952327-G |
| [30] | Haugen K B, Sun L. Firoozabadi A. Multiphase equilibrium calculations for compositional simulation[C]. SPE 106045, 2007. |
 2015, Vol. 37
2015, Vol. 37


