2. 中国石油天然气管道工程有限公司, 河北 廊坊 065000;
3. 中国石油天然气管道局, 河北 廊坊 065000
2. China Petroleum Pipeline Engineering Corporation, Langfang, Hebei 065000, China;
3. China Petroleum Pipeline Bureau, Langfang, Hebei 065000, China
管道运输是天然气最主要的运输方式,而且多以埋地管道为主。由于管道所受到的腐蚀作用,输气管网本身的一些问题(主要的是质量问题),人类的破坏,以及来自地震的毁灭性的破坏,天然气输气管网的泄漏问题有时候是不可避免的。一旦发生泄漏事故,考虑到天然气的燃烧扩散特点(易爆炸性和易扩散性),将给人类和人类赖以生存的环境带来严重的影响,因此对于天然气输气管网泄漏后的泄漏范围(危险区域范围和安全区域范围)的研究计算显得尤为重要[1-5]。国内外学者已对天然气泄漏后扩散的一般规律和模拟结果进行分析。得出一些编程相对简单、计算快的半经验半理论计算公式,但其结果的准确性很大程度上依赖于有害气体的扩散条件,如泄漏类型、自然风向和强度、大气压力梯度分布、周围地形建筑等与模型假设的接近程度[6-8]。国内学者朱红钧等对平坦地区天然气泄漏进行二维数值模拟[9],得出了泄漏后一定范围内的安全区域。马存栋研究了高压天然气输气管道发生泄漏事故时气体移动扩散的规律[10]。文献[11]采用特征线法进行天然气管道泄漏模拟,采用储罐和管道的零维模型来建立,由于孔洞导致的压力下降和气体泄漏过程的模型,这些储罐和管道的模型适合小孔洞或完全断裂工况下的仿真。前人对天然气泄漏问题的研究适用条件有局限性,且多为二维情况,虽有少数学者对三维问题进行研究,但所建立的模型只有地上的部分,无埋地管道模型,研究的结果都是在忽略了埋深的条件得出的,其结果不够精确,与实际情况相差较大。
对埋地天然气管道泄漏进行三维数值模拟,考虑到天然气泄漏后会经过土壤而泄漏到大气当中,而土壤为多孔介质,在多孔介质的内部,流体的流动以及相变过程很复杂,而有限容积法是处理这类问题较为常用的方法[12-17],采用有限容积法为原理的计算流体力学软件研究埋深地泄漏扩散的影响,并只针对埋深作为单一变量,其他气候条件地理条件均相同。首先对以往忽略埋深的工况进行研究,对其准确与否进行讨论,并对不同埋深管道泄漏进行模拟,分别研究了埋深对地下、地表和空气中的泄漏情况,且定量证明了埋深对泄漏的重要性。为事故后确定泄漏范围和危险区域提供了理论依据。
1 计算模型流体流动遵循动量守恒定律,忽略温度对流动的影响。模型主要包含质量守恒方程、动量守恒方程和组分守恒方程,其中,动量守恒方程为
| $ \begin{matrix} \frac{\partial \left( \rho {{u}_{i}} \right)}{\partial t}+\frac{\partial \left( \rho u{{u}_{i}} \right)}{\partial i}=-\frac{\partial p}{\partial i}+\frac{\partial }{\partial x}\left( {{\mu }_{\text{eff}}}\frac{\partial {{u}_{x}}}{\partial i} \right)+ \\ \frac{\partial }{\partial y}\left( {{\mu }_{\text{eff}}}\frac{\partial {{u}_{y}}}{\partial i} \right)+\frac{\partial }{\partial z}\left( {{\mu }_{\text{eff}}}\frac{\partial {{u}_{z}}}{\partial i} \right)+{{S}_{i}} \\ \end{matrix} $ | (1) |
式中:i=x, y, z;
Sx=0;
Sy=0
Sz=gβT (T0 − T)
ρ—流体密度,kg/m3;
ux、uy、uz — x、y,z向的速度分量,m/s;
t —时间,s;
u—速度矢量,m/s;
p—流体压强,Pa;
µeff —有效黏度,Pa·s;
g—重力加速度,g=9.8 m/s2;
βT —体积膨胀系数,无因次;
T0 —参考温度,K;
T —温度,K。
天然气输气管道发生泄漏事故规模的大小可以按照泄漏口的大小进行划分,而且孔径较小的泄漏事故发生的概率较大一些,孔径较大的泄漏事故发生的概率则相对较小。假设所研究的泄漏过程为泄漏口孔径为较小的情况,而且从孔径中排出气体的过程看做是绝热过程,认为天然气为理想气体。由伯努利方程以及绝热方程可以得到,泄漏口的气体流速
| $ {{v}_{0}}=\varphi \sqrt{\frac{2k}{k-1}\text{R}{{T}_{1}}\left[1-{{\left( \frac{{{p}_{0}}}{{{p}_{1}}} \right)}^{\frac{k-1}{k}}} \right]} $ | (2) |
式中:
v0 —泄漏速度,m/s;
φ—流速系数,无因次,代表实际流速与理论流速之比,一般为0.97~0.98;
k —绝热指数,无因次,对于天然气一般取1.3;
R—气体常数,R=8.314 J/(mol·K);
T1 —气体温度,K;
p0 —环境压力,Pa;
p1 —气体泄漏前压力(管道内介质压力),Pa。
由于孔口形状不同,引入流量系数,则体积流量为
| $ Q={{C}_{\text{D}}}{{p}_{1}}A\varphi \sigma \sqrt{\frac{M}{\text{R}{{T}_{1}}}} $ | (3) |
式中:
Q—体积流量,m3/s;
CD —流量系数,无因次;
A—泄漏孔面积,m2;
M —分子量,天然气取0.017 kg/mol;
σ—速度系数,无因次。
式(3)的流量系数CD,亦称泄漏系数。一般取值在0.6~1.0,对圆形孔,CD=1.0;三角孔,CD=0.95;长形孔,CD=0.90;孔口为内层腐蚀形成的减缩孔,0.9 < CD < 1.0;孔口为外力机械损伤形成渐扩孔,0.6 < CD < 0.9。本文选圆形孔,CD=1.0。
泄漏口的气体流速与流体的流动状态有很大关系,所以在研究泄漏过程前要先确定气体的流动状态(音速或亚音速)。在长输气体管道中由于介质压力较高,气体处于流速临界状态,流动属于音速流动,即
| $ \sigma =\sqrt{k{{\left( \frac{2}{k+1} \right)}^{\frac{k+1}{k-1}}}} $ | (4) |
气体从泄漏口出来,可以按射流处理,沿射流中心方向上的速度可表示为
| $ {{v}_{\text{m}}}=\frac{0.965}{\frac{as}{{{d}_{\text{l}}}}+0.294}{{v}_{0}} $ | (5) |
式中:vm —圆断面射流的轴心速度,m/s;dl —泄漏孔半径,m;a—紊流系数,无因次;s—到射流出口的距离,m。
由于土壤对泄漏气体的阻碍作用,从泄漏口到地表这段距离,气体的泄漏速度可以看做是分层递减的,为简化分析计算,将递减过程近似为均匀递减,则当气体泄漏到地表时会形成一个等半径的圆形的泄漏区域,此时的气体泄漏速度才是更为准确的,为简化计算,实际泄漏速度应该为射流乘以一个小于1的速度调整常数α
| $ {{v}_{\text{r}}}=\alpha {{v}_{\text{m}}} $ | (6) |
式中:α—沿程速度修正系数,无因次,与通过土壤性质有关。
根据天然气的泄漏特点,天然气通过管道泄漏口射出管外,对于埋地天然气输气管道,泄漏刚开始时,气体射入土壤中,气体在流动过程中会受到来自土壤的孔隙阻力以及毛细管压力,其泄漏速度将会在一定的程度上减小。由式(5)可知,地表速度的大小在不计其他耗省的工况中受射流距离的影响很大;由式(6),对于埋地天然气泄漏射流距离即管道埋深对地表泄漏速度的影响更大,而地表泄漏速度的大小将决定气体扩散到大气中的初速度,进而影响扩散范围。
2 计算实例 2.1 实例参数选取平坦地区泄漏工况,有埋深的情况模拟区域尺寸为:40.0 m×40.0 m×40.0 m,其中y方向范围为(-10,30),即空气域高度为30 m;不计埋深的时模拟区域尺寸为40.0 m×30.0 m×40.0 m,其中y方向范围为与前面一致。定义管道与地表的最近距离为埋深。管道外径1.0 m,泄漏口直径0.3 m,管内和环境温度300 K,土壤含水率9%。漏口气体流速为5 m/s,泄漏口方向向上,天然气中甲烷和硫化氢的浓度分别为93.5%和6.5%。网格模型如图 1所示,网格中红色为空气域,蓝色为土壤域。
 |
| 图1 网格模型 Fig. 1 Mesh model |
其中,图 1a为忽略埋深时仰视网格图,黑色密集中心位置为泄漏口,红色密集中心区域为泄漏口正上方,图 1b、图 1c分别为有埋深时管道附近网格图、管道及泄漏口的计算网格图。
2.2 忽略埋深的不准确性同一工况的天然气泄漏事故,当环境因素和泄漏速度相同时,管道的埋深对天然气的泄漏扩散范围影响很大。先对忽略埋深的不准确性进行验证。
图 2中给出了泄漏10 s和泄漏60 s时不同埋深工况地表以上1.0 m高处平面中同样位置各点的甲烷和硫化氢质量分数。对于泄漏10 s的情况,由图 2a、图 2b可以得出,在平面内同样位置忽略埋深的情况甲烷和硫化氢的质量分数都比埋深为1.4 m和2.0 m的情况甲烷的质量分数大的多,而埋深为1.4 m和2.0 m的情况甲烷和硫化氢的质量分数相差不大。对于泄漏60 s的情况,由图 2c、图 2d可以得出,泄漏60 s时忽略埋深的情况甲烷和硫化氢的质量分数仍然比埋深为1.4 m和2.0 m的情况大,但大小差距相对泄漏10 s时有所下降。
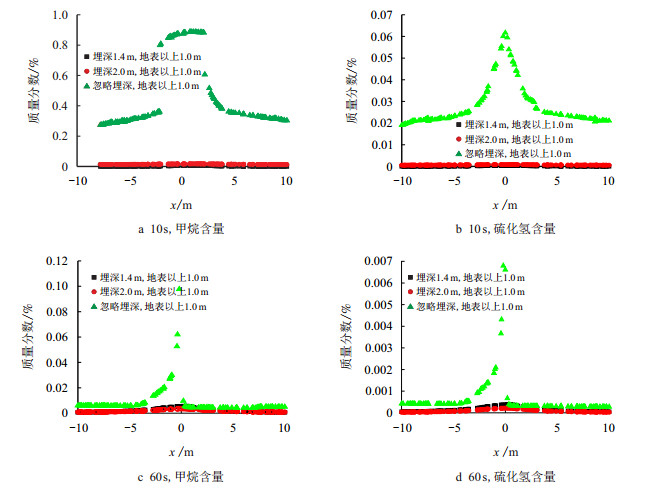 |
| 图2 不同埋深工况下,地表以上1.0 m高处平面上同一位置天然气扩散速度 Fig. 2 The diffusion velocity of natural gas at the same location of the same plane under different burial depth conditions |
所以,无论是同一时刻还是不同时刻甲烷和硫化氢的质量分数忽略埋深的情况总是比埋深为1.4 m和2.0 m的情况大,可以得出模拟过程中忽略埋深即忽略埋深所得出的各项结果都有很大的误差,忽略埋深是不准确的,所以下文对埋深为1.4 m和2.0 m的工况进行研究,在考虑埋深的基础上研究埋深对泄漏的影响。
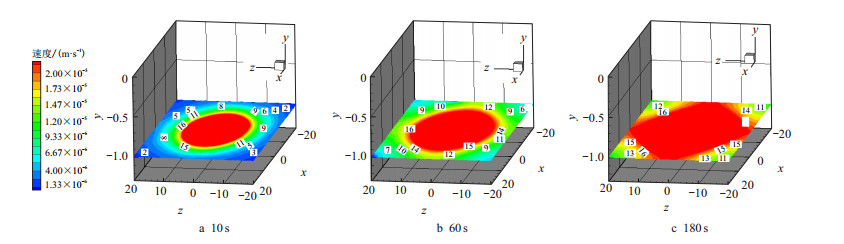
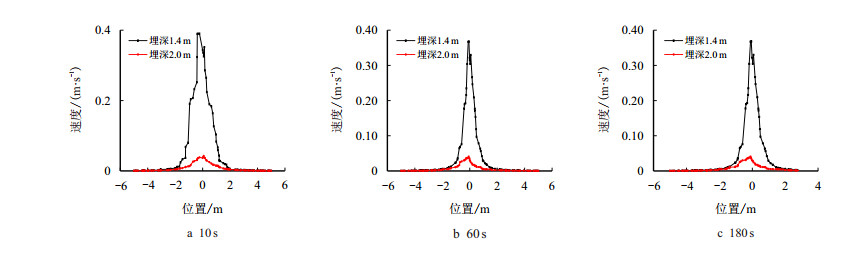
2.3 埋深对天然气泄漏扩散的影响为研究埋深对天然气泄漏扩散的影响,分别研究了地下、地表和空气中天然气的泄漏情况。图 3、图 4分别给出了该平面内埋深为1.4 m和2.0 m时不同时刻天然气质量分数流场图,图 5为泄漏过程中该平面速度散点图。
 |
| 图3 埋深1.4 m地表下1.0 m深处平面内天然气泄漏后的流场图 Fig. 3 The velocity of natural gas below the surface of the deep 1.0 m under 1.4 m burial depth conditions |
 |
| 图4 埋深2.0 m地表下1.0 m深处平面内天然气泄漏后的流场图 Fig. 4 The velocity of natural gas below the surface of the deep 1.0 m under 2.0 m burial depth conditions |
 |
| 图5 不同埋深地表以下1.0 m深处平面内天然气泄漏后的速度散点图 Fig. 5 The leakage natural gas velocity below the surface of the deep 1.0 m under different burial depth conditions |
由图 3、图 4可以得出,天然气的扩散范围在一定时间内与时间成正比,分别对比图 3a和图 4a,图 3b和图 4b,图 3c和图 4c可以看出,相同时刻埋深1.4 m比埋深2.0 m硫化氢的扩散范围大,又由图 5a中可以看出泄漏过程中埋深1.4 m比埋深2.0 m泄漏速度大,尤其是位置0处(泄漏口上方对应的位置),速度越大相同时间内泄漏的天然气就越多,其质量分数就会越大,验证了图 3、图 4。图 5b与5c中速度相差无几,说明此时该平面内速度已经稳定。综合图 3∼ 图 5可以得出,此平面内无论是扩散范围、泄漏速度、还是质量分数埋深1.4 m都比埋深2.0 m大,即埋深为扩散范围、泄漏速度、质量分数的减函数,埋深越小扩散范围、泄漏速度、质量分数越大。
对泄漏过程中地表处的天然气平均速度和质量分数进行跟踪监测得到图 6。其中图 6a、图 6b为地表处天然气平均速度随时间的变化,图 6c为地表处天然气质量分数随时间的变化。泄漏30 s之前同一部分面域内同样位置泄漏速度散点图,由图 6a可以看出泄漏10 s时两种埋深工况下泄漏速度都是中间大两边小,同样的位置埋深1.4 m都比埋深2.0 m速度大,图 6b、图 6c中为了看的更清晰减少了位置节点,可以看出这两个时刻泄漏速度中间高两边低的特点不是很明显但同样的位置埋深1.4 m还是都比埋深2.0 m速度大。分析其原因可能为:高速气流从泄漏口喷出,大量高浓度天然气迅速充满泄漏口附近地带,由于埋深的存在,天然气速度会受土壤阻碍作用速度会减小,由此可知经过越大范围的土壤层其速度会减小的越大。可以得出埋深与泄漏速度成反比,埋深越小泄漏地表速度越大。
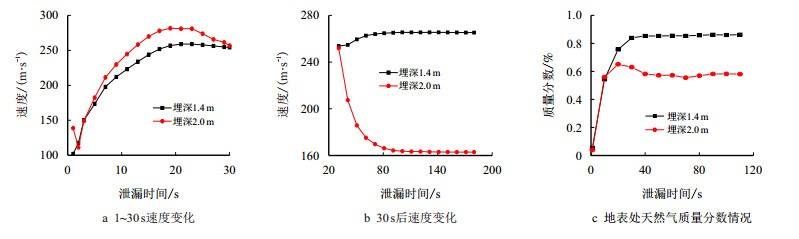 |
| 图6 不同埋深地表以下1.0 m深处平面内天然气泄漏后的速度、质量分数变化图c Fig. 6 The changes of leakage natural gas velocity and mass fraction below the surface of the deep 1.0 m under different burial depth conditions |
图 7~图 8为不同埋深整个模拟范围内空气域中天然气的泄漏扩散范围3D显示。
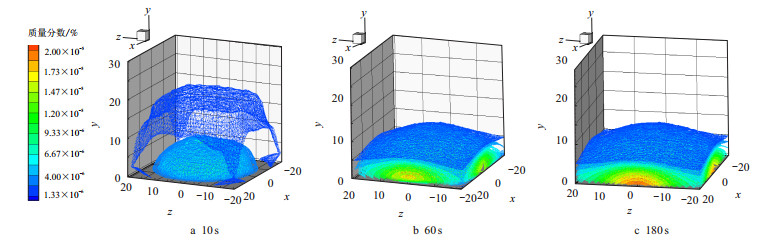 |
| 图7 埋深1.4 m,空气中天然气泄漏情况 Fig. 7 The leakage situation of natural gas in the air at 1.4 m burial depth |
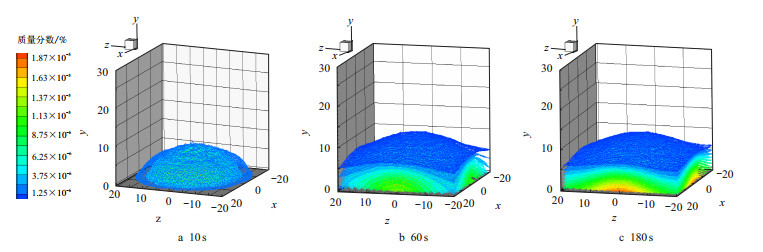 |
| 图8 埋深2.0 m,空气中天然气泄漏情况 Fig. 8 The leakage situation of natural gas in the air at 2.0 m burial depth |
可以看出10 s时天然气还未扩散到模拟范围边界,随着泄露的进行扩散范围越来越大,60 s时已经扩散到边界,其原因同图 6中结论:埋深越深,地表泄漏速度越小。综合图 7、图 8可以得出埋深与扩散范围成、高浓度范围反比,埋深越小扩散范围越大、高浓度范围越大。
为了更加清楚直观地分析管道埋深对天然气泄漏的影响,对相关数据进行分析处理,做出不同埋深危险边界的覆盖范围3D图,如图 9所示。由3D图可以清楚地看出埋深为1.4 m的工况危险范围大于埋深2.0 m的工况。其原因为:管道埋于地下,泄漏初期大量气体首先扩散到土壤中,受土壤孔隙阻力、毛细管压力的影响,埋于地下的深度越大,气体湍动能的损失越大。
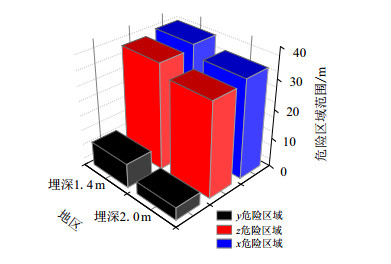 |
| 图9 不同埋深,空气中天然气泄漏准确范围 Fig. 9 The accurate leakage range of natural gas in the air at different burial depth conditions |
(1) 管道泄漏后相同条件下硫化氢的危险区域总是比甲烷的危险区域大,建议事故处理时首先考虑硫化氢的危险区域。
(2) 忽略埋深将导致硫化氢轴向危险区域扩大化,地表危险区域比实际情况小,得出的危险区域结果不精确。对于轴向,埋深对静风天气下硫化氢的危险区域影响较大,忽略埋深的比有埋深的危险区域大;埋深对有风天气硫化氢的危险区域影响不大,但对扩散范围影响较大,扩散范围忽略埋深的比有埋深的大。对于地表,埋深对静风天气下硫化氢的危险区域影响较大,忽略埋深的比有埋深的小但扩散范围忽略埋深的比有埋深的大;埋深对有风天气硫化氢危险区域影响不大但扩散范围有埋深的比忽略埋深的大。
(2) 对埋深1.8 m,泄漏口速度243.42 m/s,风速为5 m/s工况进行数值模拟。研究结果表明,含硫化氢6.5%的高含硫天然气泄漏690 s时达到稳定,径向危险区域约为(-170,80),轴向危险区域约为(-435,122),高度达到40 m左右。可为事故后抢险救灾提供较为准确的危险区域预测。
| [1] | 秦政先.天然气管道泄漏扩散及爆炸数值模拟研究[D].南充:西南石油学院, 2006:1-5. |
| [2] | 毕静, 张默, 何利民. 天然气管道泄漏扩散规律CFD研究现状分析[J]. 石油地质与工程, 2012 (6) : 1291 –131. |
| [3] |
赵洪华, 艾长胜. 管道传声特性及典型破坏声的识别[J].
中国石油大学学报:自然科学版, 2006, 30 (3) : 101 –105.
Zhao Honghua, Ai Changsheng. Pipeline acoustic propagation features and recognition of typical damage sounds[J]. Journal of China University of Petroleum:Edition of Natural Science, 2006, 30 (3) : 101 –105. |
| [4] |
李振林, 姚孝庭, 张永学, 等. 基于FLUENT的高含硫天然气管道泄漏扩散模拟[J].
油气储运, 2008, 27 (5) : 38 –41.
Li Zhenlin, Yao Tingxiao, Zhang Yongxue, et al. Simulation study on leakage and dispersion of high sulfur nature gas pipeline with FLUENT CFD-based software[J]. Oil & Gas Storage and Transportation, 2008, 27 (5) : 38 –41. |
| [5] |
李朝阳, 马贵阳. 埋地与架空输气管道泄漏数值模拟对比分析[J].
天然气工业, 2011, 31 (7) : 90 –93.
Li Zhaoyang, Ma Guiyang. A comparative study of numerical simulation on underground and aerial pipeline leakage at instantaneous and continuous states[J]. Natural Gas Industry, 2011, 31 (7) : 90 –93. |
| [6] |
钱新明, 冯长根. 易燃易爆危险物质泄漏扩散仿真及其应用的研究[J].
中国安全科学学报, 1997, 7 (3) : 30 –33.
Qian Xinming, Feng Changgen. Study on simulationand application of the release and dispersion of flammableand explosivematerials[J]. Journal of China Safety Science, 1997, 7 (3) : 30 –33. |
| [7] | Sagrado A P G, van Beeck J, Rambaud P, et al. Numerical and experimental modelling of pollutant dispersion in a street canyon[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90 (4) : 321 –339. |
| [8] | Berkowicz R. Modelling street canyon pollution:model requirements and expectations[J]. International Journal of Environment and Pollution, 1997, 8 (3) : 609 –619. |
| [9] |
朱红钧, 林元华, 马成学, 等. 平坦地区含硫化氢集输管道的泄漏扩散模拟[J].
西南石油大学学报:自然科学版, 2009, 31 (6) : 156 –157.
Zhu Hongjun, Lin Yuanhua, Ma Chengxue, et al. Numerical smulation of sulfured hydrogen-contaning gas pipeline leak and diffusion on flat areas[J]. Joumal of Southwest Petroleum University:Edition of Natural Science, 2009, 31 (6) : 156 –157. |
| [10] | 马存栋. 高压天然气管道破裂气体扩散规律模拟结果分析[J]. 油气田地面工程, 2005, 24 (3) : 8 –10. |
| [11] | Liu Y, Zheng J. Numerical simulation of the diffusion of natural gas due to pipeline failure[C]//ASME 2007 pressure vessels and piping conference. American Society of Mechanical Engineers, 2007:319-325. |
| [12] | 卢涛, 姜培学. 多孔介质融化相变自然对流数值模拟[J]. 工程热物理学报, 2005, 26 (1) : 167 –170. |
| [13] | 卢涛, 佟德斌. 饱和含水土壤埋地原油管道冬季停输温降[J]. 北京化工大学学报, 2006, 33 (4) : 37 –40. |
| [14] | Beckermann C, Viskanta R. Natural convection solid/liquid phase change in porous media[J]. International Journal of Heat and Mass Transfer, 1988, 31 (1) : 35 –46. DOI:10.1016/0017-9310(88)90220-7 |
| [15] | Wang B X, Du J H. Forced convective heat transfer in a vertical annulus filled with porous media[J]. International Journal of Heat and Mass Transfer, 1993, 36 (17) : 4207 –4213. DOI:10.1016/0017-9310(93)90083-I |
| [16] | Hamdami N, Monteau J Y, Le Bail A. Simulation of coupled heat and mass transfer during freezing of a porous humid matrix[J]. International journal of refrigeration, 2004, 27 (6) : 595 –603. DOI:10.1016/j.ijrefrig.2004.03.016 |
| [17] |
李又绿, 姚安林, 李永杰. 天然气管道泄漏扩散模型研究[J].
天然气工业, 2004, 24 (8) : 102 –104.
Li Youlü, Yao Anlin, Li Yongjie. Study on diffusion of gas pipeline leaking[J]. Natural Gas Industry, 2004, 24 (8) : 102 –104. |
 2015, Vol. 37
2015, Vol. 37


