石油机械中的摩擦磨损问题一直是研究热点,比如牙轮钻头中滑动轴承的摩擦与润滑,套管与管柱之间的摩擦,扶正器的磨损,泥浆泵和压缩机中活塞与缸套之间的摩擦问题等。由于磨损造成的零部件失效一直是制约石油装备发展的重要因素之一,因而深入研究其摩擦问题对中国石油装备产业的发展具有重要意义。
当两个物体表面相互接触时,从微观上看是两个粗糙表面上一系列微凸体的接触,具有接触的不均勻性[1]。而粗糙表面的接触行为对摩擦、磨损、润滑、密封和传热有着重要的影响[2]。由于摩擦表面的真实接触面积远小于名义接触面积且不连续,使得接触区域的温升远高于摩擦表面的平均温升,导致了温度分布不均勻,引起摩擦副表面受热变形不均勻,从而改变了两表面的接触状态,又影响了摩擦副表面的温度分布[1]。因而,两粗糙表面之间的滑动摩擦过程是一个复杂过程,属于典型的热机耦合问题。同时,摩擦磨损与两接触表面的微观形貌和接触特性有着重要的关系,微凸体的形貌直接影响接触区的应力状态。因此,研究粗糙表面在滑动摩擦中的温度与应力有重要的应用价值。
国内外学者对粗糙表面之间的接触问题进行了大量的研究,如,1966年Greenwood J A和Williamson B P[3]提出了基于统计分析的粗糙表面和光滑表面之间弹性和弹塑性混合接触模型,即G-W模型,预测了真实接触面积与法向载荷间的关系;Wang Q和Liu G[4-5]提出了一种计算两个无限大粗糙平面的有限元二维热机接触模型,采用了数字化轮廓微凸体,研究了热弹性、稳态热传导及接触界面之间的相互作用问题;Huang J H和Ju F D[6]认为二维形貌不能反映真实工程表面,需要对三维热机模型进行分析;Polonsky I A等[7]将共轭梯度法和快速傅里叶变换结合提出了三维热弹性接触模型;Gong Z Q等[8]基于弹性光滑的半无限与刚性、绝热的分形粗糙体的接触,建立了热机耦合模型;Robert LJ等[9]实现了两球状微凸体的相对滑动接触,但未考虑各微凸体的相互作用及热力耦合; Hasan S等[10]运用有限元法研究了二维刚性粗糙体与光滑弹性-理想塑性平面的滑动接触问题;Liu G等[11]基于稳态热传导对工程粗糙表面微凸体进行了三维热机耦合分析;黄健萌等[1, 12]建立了规则形状微凸体、三维分形特性微凸体与理想刚性平面接触的热力耦合模型,并通过有限元软件ANSYS对其摩擦过程中的热、力进行了数值模拟;杨国庆等[13]建立了两个微观粗糙表面的接触有限元模型,分析了不同载荷下微观结合面的变形、接触压力和真实接触面积等特性。虽然已经有很多学者对粗糙表面的接触问题进行了研究,但未考虑微凸体之间的相互作用和影响,或未研究相对运动参数对摩擦生热的影响。
Greenwood J A等认为通过假定球形微凸体的半径按某种规律变化,可以得到真实接触面积与法向载荷的正比关系[14]。因而,基于G-W弹性接触模型,本文建立了粗糙面的滑动接触有限元计算模型,将两粗糙表面简化为具有球形微凸体的粗糙表面与理想平面,模拟并分析了粗糙表面的摩擦生热及热应力变化规律,研究了摩擦系数、相对运动速度及初始变形量对粗糙面热、力的影响。
1 热机耦合计算模型 1.1 热传导基本方程根据Fourier传热定律和能量守恒定律,对于无内热源的各向同性材料,可以建立其热传导方程:
| $ \frac{{{\partial }^{2}}T}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}T}{\partial {{y}^{2}}}+\frac{{{\partial }^{2}}T}{\partial {{z}^{2}}}=\frac{\rho C}{k}\frac{\partial T}{\partial t}\text{ } $ | (1) |
式中:
T—温度,K;
t—时间,s;
ρ—材料密度,kg/m3;
C—材料比热容,J/(kg·K);
k—材料热导率,W/(m·K)。
1.2 对流边界条件由牛顿冷却公式可知,单位时间内,单位面积上对流传热的热量为
| $ \varphi =hA({{T}_{\text{f}}}\text{-}{{T}_{\text{w}}}) $ | (2) |
式中:
h—换热系数,W/(m2· ℃);
A—接触面积,m2;
Tw—接触面温度,℃;
Tf—介质温度,℃。
两表面与空气之间的热交换是其主要放热形式。由于理想表面发生运动,其外表面为强迫对流换热,粗糙体保持固定不动,其外表面可视为自然对流换热。取粗糙体外表面的对流换热系数为常数,20 W/(m2·℃)。
1.3 摩擦热量的分配摩擦产生的热量要分别传给粗糙体和理想平面,热量分配计算式为[15]
| $ \frac{{{q}_{1}}}{{{q}_{2}}}=\sqrt{\frac{{{C}_{1}}{{\rho }_{1}}{{k}_{1}}}{{{C}_{2}}{{\rho }_{2}}{{k}_{2}}}} $ | (3) |
式中:
C1,C2—对应材料的比热容,J/(kg·K);
ρ1,ρ2—对应材料的密度,kg/m3;
k1,k2—对应材料的热导率,W/(m·K)。
可知,在摩擦生热过程中,热量会更多地传人导热性能比较好的材料。
1.4 基本假设热机耦合理论模型的基本假设:(1)两部件的材料组成均匀,且各向同性;(2)部件的密度、比热、热导率、热膨胀系数、弹性模量、泊松比等物理参数为常数,且不受温度变化影响[16]; (3)仅考虑热传导和热对流效应,忽略热辐射的作用;(4)忽略粗糙体的磨损及其影响,认为动能全部转化为摩擦热而被摩擦副吸收;(5)摩擦过程中,符合库仑摩擦定律,且认为摩擦因数保持不变[12]。
2 有限元计算模型粗糙体表面的微观形貌如图 1所示,微凸体为球体且采用正方形排列,定义微凸体的半径R=80 µm,微凸体的高度h=40 µm,微凸体之间的间距l=320 µm, 粗糙体的厚度h'=200 µm。定义量纲参数l/R表征粗糙体的表面粗糙度,l/R值越大则说明粗糙体的表面粗糙度越大。对三维模型采用六面体网格进行划分,划分后的有限元模型如图 2所示。
 |
| 图1 粗糙体模型 Fig. 1 The rough body model |
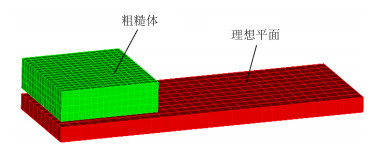 |
| 图2 有限元模型 Fig. 2 Finite element model |
两部件材料的热物理参数如表 1所示。两表面之间的摩擦因数f=0.2。由于热机耦合计算较为复杂,为节约计算时间,取滑移距离为2 000 µm。对粗糙体的5个外表面分别施加法向约束,载荷分为两步:第一步对理想平面施加位移载荷,使其对粗糙表面形成一定的压人量λ=0.8 µm; 第二步对理想平面施加速度载荷v=2 m/s。
| 表1 材料物理参数 Table 1 Material physical parameters |
图 3为粗糙体的温度场分布切片,微凸体的顶部温度达到了最大值,而且整个微凸体的温度普遍高于粗糙体基体的温度。在1 ms时刻,微凸体的最高温度达73.52 ℃,而粗糙体基体的温度基本还保持在20 ℃左右,主要是由于粗糙体在垂直于滑动表面方向的热梯度非常大,热量基本都集中在滑动表面方向,来不及向粗糙体基体内部传导,从而导致粗糙体表面的“闪温”过高。同时,由于外力的作用粗糙体的接触面发生弹性变形,而摩擦温升又会改变接触面的形变及热应力值。
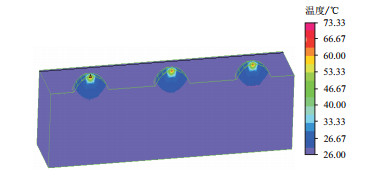 |
| 图3 粗糙体的温度场分布 Fig. 3 Temperature distribution of rough body |
图 4为粗糙体的等效应力分布云图,由图可以看出,粗糙体的高应力区域主要集中在微凸体部分,其他部分的热应力值较小。通过观察微凸体部分的热应力变化,在发生相对运动以前的最大等效应力为454.6 MPa, 而在运动结束后应力值变为535.0 MPa, 增长率为17.7%。说明摩擦生热对粗糙表面的等效应力影响较大。而且在发生滑移以前,微凸体内部的等效应力沿垂直接触面的球体直径成轴对称分布;当两接触面发生相对运动后,微凸体内部的应力分布也发生了变化,高应力区域偏向了滑移方向一侧,在滑移方向一侧的球面上出现了一个应力集中区;整个微凸体的最大等效应力并不出现在接触表面,而是在接触面以下位置。粗糙体表层应力值的变化又加剧了微凸体的热弹性变形,改变了摩擦副的接触状态,进而影响温度的分布,因而,热机耦合过程是一个各种因素相互影响的过程。
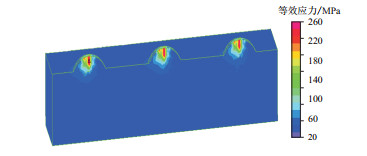 |
| 图4 粗糙体的等效应力分布 Fig. 4 Equivalent stress distribution of rough body |
图 5为微凸体表面接触应力随运动时间的变化曲线。可以看出,接触应力经历了一个快速上升和缓慢增长的阶段。发生相对运动前,粗糙峰的法向接触应力值为442.7MPa, 运动结束后为517.2MPa, 增长了16.8%。说明粗糙峰接触应力受表面温升的影响较大。
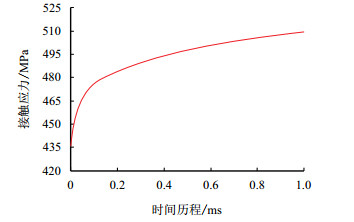 |
| 图5 接触应力随时间变化历程 Fig. 5 Contact stress changing course with time |
相对运动速度是表征滑移运动的最主要参数,它的数值大小对滑动摩擦过程产生重要的影响。图 6为不同的相对滑动速度下,滑动2 mm时粗糙体表面最高温度随位移量的变化历程。可以将温度变化曲线划分为两个阶段,第一个阶段为急速增长阶段,第二阶段为缓慢增长阶段。可以发现,相对运动速度越高,温度变化的第一个阶段持续运动的位移量就越大,而且速度越大,温度在第二阶段的变化量也越大。当速度分别为0.5, 2.0, 5.0和10.0 m/s时,粗糙峰温度变化第一个阶段对应的位移量分别为0.04, 0.12, 0.30和0.60 mm。
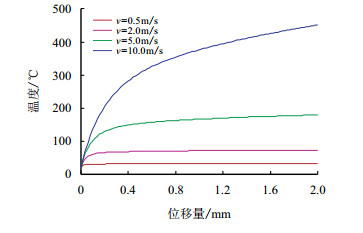 |
| 图6 不同速度下的温度变化历程 Fig. 6 Temperature changing course under different speeds |
不同相对滑动速度下,粗糙体在运动结束时的最大等效应力和法向接触应力如图 7所示。可知,相对滑动速度对粗糙体的等效应力和接触应力的影响规律不同。
 |
| 图7 不同速度下的应力值 Fig. 7 The stresses under different speeds |
初始运动时刻,理想平面对粗糙体的压入量不同时,粗糙体表面的应力值和变形量不同,则在运动过程中产生的热量就不相同,进而影响了最高温升和温度分布。图 8为不同的初始压入量下,粗糙体表面的最高温升随运动时间变化历程。虽然初始压入量不同,但最高温度变化经历第一个阶段的时间较为接近,基本均在0.05 ms时刻温度曲线发生突变。压入量越大,粗糙体表面温度达到近似平衡状态时的温度值就越大,即在滑移过程中产生的热量越多,而且温度值在第二个阶段的增长量也略大。图 9为1 ms时刻粗糙体表面最大等效应力和接触应力随初始压入量的变化,初始压入量对二者应力值的影响规律基本相同,它们与压入量近似成线性关系。
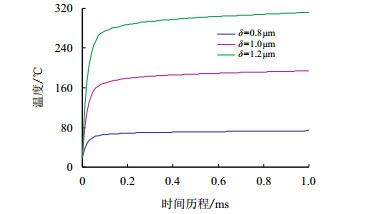 |
| 图8 不同压入量下的温度变化历程 Fig. 8 Temperature changing course under different pressure intakes |
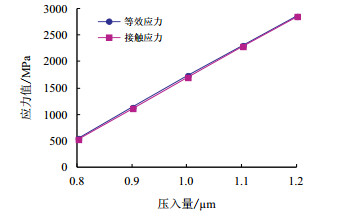 |
| 图9 不同压入量下的应力值 Fig. 9 Stresses under different pressure intakes |
表征两摩擦表面摩擦状态的一个重要参数就是摩擦因数,它直接影响接触面之间的摩擦生热量和接触应力大小。图 10为两接触表面的摩擦因数不同时,粗糙体表面的最高温度变化曲线。摩擦因数越大时,接触面之间产生的热量就越多,温度变化的第一个阶段持续的时间略长。当摩擦因数分别为0.1,0.2, 0.3和0.4时,第一阶段的持续时间分别对应为0.05, 0.08, 0.11和0.14 ms。同时在该阶段的温度增长率也越大,温度在第二个阶段的变化量也随摩擦因数的增大而增大。图 11为1 ms时粗糙体的最大等效应力和接触应力随摩擦因数的变化规律。可见,二者均随摩擦因数的增大而增加。但是,随着摩擦因数的增大,最大等效应力的增长量更大,说明摩擦因数对等效应力的影响大于其对接触应力的影响。
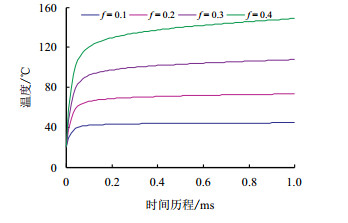 |
| 图10 不同摩擦因数下的温度变化历程 Fig. 10 Temperature changing course under different friction coefficients |
 |
| 图11 不同摩擦因数下的应力值 Fig. 11 Stresses under different friction coefficients |
(1) 粗糙体的热量主要集中在滑动表面,粗糙体表面的微凸体上出现局部高温区,而且滑移过程中微凸体的高应力区偏向了滑移方向一侧,与静态接触中应力分布不同。
(2) 粗糙体表面最高温度随运动时间的变化过程可分为急剧增长和缓慢增长两个阶段。相对运动速度越高,最高温度在第一个变化阶段的持续位移量就越大;采用不同的压入量时,温度变化的第一个阶段持续的时间基本均为0.05 ms; 随着摩擦因数的增大,温度变化的第一个阶段持续的时间略长。
(3) 粗糙体表面的最大接触应力与等效应力随着运动速度的增大而增大;初始压入量与粗糙体表面最大等效应力和接触应力值呈近似线性变化;摩擦因数对等效应力值的影响大于其对接触应力值的影响。
| [1] |
黄健萌, 高诚辉, 李友遐. 粗糙表面基于G-W接触的三维瞬态热结构分析[J].
机械强度, 2008, 30 (6) : 959 –964.
Huang Jianmeng, Gao Chenghui, Li Youxia. Transient coupled thermo-mechanical analysis of rough surface based on G-W model[J]. Journal of Mechanical Strength, 2008, 30 (6) : 959 –964. |
| [2] |
魏龙, 顾伯勤, 冯飞, 等. 粗糙表面接触模型的研究进展[J].
润滑与密封, 2009, 34 (7) : 112 –115.
Wei Long, Gu Boqin, Feng Fei, et al. Progress of study on contact models of rough surfaces[J]. Lubrication Engineering, 2009, 34 (7) : 112 –115. |
| [3] | Greenwood J A, Williamson B P. Contact of nominally flat surfaces[J]. Proceedings of Royal Society, 1966, A295 (3) : 300 –319. |
| [4] | Wang Q, Liu G. A thermo-elastic asperity contact model considering steady-state heat transfer[J]. Tribology Transaction, 1999, 42 (4) : 763 –770. DOI:10.1080/10402009908982280 |
| [5] | Liu G, Wang Q. Thermoelastic contact, frictional shear, and parameter correlations[J]. ASME Journal of Tribology, 2000, 122 (1) : 300 –307. DOI:10.1115/1.555357 |
| [6] | Huang J H, Ju F D. Thermo-mechanical cracking due to moving frictional loads[J]. Wear, 1985, 102 (1-2) : 81 –104. DOI:10.1016/0043-1648(85)90093-6 |
| [7] | Polonsky I A, Keer L M. A fast and accurate method for numerical analysis of elastic layered contacts[J]. ASME Journal of Tribology, 2000, 122 (1) : 30 –35. DOI:10.1115/1.555323 |
| [8] | Gong Z Q, Komvopoulos K. Thermomechanical analysis of semi-infinite solid in sliding contact with a fractal surface[J]. ASME Journal of Tribology, 2005, 127 (2) : 331 –342. DOI:10.1115/1.1792691 |
| [9] | Robert L J, Ravi S D, Hasnain M, et al. An analysis of elasto-plastic sliding spherical asperity interaction[J]. Wear, 2007, 262 (1-2) : 210 –219. DOI:10.1016/j.wear.2006.05.011 |
| [10] | Hasan S, Alaettin O. Thermomechanical analysis of elaatoplatic medium in sliding contact with fractal surface[J]. Tribology International, 2008, 41 (8) : 783 –796. DOI:10.1016/j.triboint.2008.01.010 |
| [11] | Liu G, Wang Q, Ao Y. Convenient formulas for modeling three-dimensional thermo-mechanical asperity contacts[J]. Tribology International, 2002, 35 (7) : 411 –424. DOI:10.1016/S0301-679X(02)00022-1 |
| [12] |
黄健萌, 高诚辉. 弹塑性粗糙体/刚体平面滑动摩擦过程热力耦合分析[J].
机械工程学报, 2011, 47 (11) : 87 –92.
Huang Jianmeng, Gao Chenghui. Thermo-mechanical research on frictional sliding between elasto-plastic rough solid and rigid flat[J]. Journal of Mechanical Engineering, 2011, 47 (11) : 87 –92. DOI:10.3901/JME.2011.11.087 |
| [13] |
杨国庆, 熊美华, 洪军, 等. 3D粗糙表面的数字化表征与接触特性分析[J].
西安交通大学学报, 2012, 46 (11) : 58 –63.
Yang Guoqing, Xiong Meihua, Hong Jun, et al. Numerical characterization and contact performances for 3D rough surfaces[J]. Journal of Xi'an Jiaotong University, 2012, 46 (11) : 58 –63. |
| [14] | Greenwood J A, Tripp J H. The contact of two nominally flat rough surfaces[J]. Proceedings of the Institution of Mechanical Engineers, 1970, 185 (48) : 625 –634. |
| [15] | 张靖周. 高等传热学[M]. 北京: 科学出版社, 2009 . |
| [16] |
孟德建, 张立军, 余卓平. 通风盘式制动器热-机耦合理论建模与分析[J].
同济大学学报:自然科学版, 2010, 38 (6) : 890 –897.
Meng Dejian, Zhang Lijun, Yu Zhuoping. Theoretical modeling and FEA of thermo-mechanical coupling dynamics of ventilated disc brake[J]. Journal of Tongji University:Natural Science, 2010, 38 (6) : 890 –897. |
 2015, Vol. 37
2015, Vol. 37


