中国东部的许多断陷盆地的油藏中,断层非常发育,断层遮挡占有主导地位,许多相邻井的油层不属于同一油藏,也不属于同一断块,现实生产中很难做出符合油藏情况的开发部署,研究断块油藏油井压力特征具有重大意义。中国学者对断块油藏方面进行了大量的研究。周路等对断层连通性及定位进行了研究[1-2];卢德唐等考虑井储和表皮效应,从试井曲线方面对两夹角断块油藏油井井底压力特征进行了研究[3];王晓冬等通过建立模型对两夹角断块油藏油井井底压力方程进行了解析求解,研究了井底压力变化特征[4]。
对于断层以不同角度相交的窄小型断块油藏,由于沉积过程中的方向性,使得油藏具有各向异性。各向异性油藏对于渗透率具有方向性,具体表现为:在地层中同一点上,流体向某一个方向流动的渗透率比其他方向大,而在与该方向垂直方向上的渗透率最小。刘月田等研究了各向异性对无限大地层油井产能及井网规划的研究[5-10];王海静等研究了各向异性对盒状油藏油井流入动态的影响[11-12];王大为等人研究了各向异性对单井或面积井网产量影响[13-15],但各向异性对两夹角断块油藏地层压力及油井井底压力影响方面的研究却不多。本文在文献[3]和文献[4]对两夹角断块油藏研究基础上,建立模型分析了各向异性对两夹角断块油藏油井井底压力特征的影响。
1 模型建立及求解 1.1 物理模型两封闭断面f1,f2围成一个等厚、无限大各向异性地层(图 1),区域渗透率主值分别为Kx,Ky,且渗透率各向异性系数为τ=Kx/Ky(τ > 1)(当τ → 0时,流体在y方向渗流速度接近为0,τ → +∞,此时模型仍然适用),区域内有一口定产井A到间断面f1,f2的距离分别为d1,d2。取两间断面交点O为坐标原点,渗透率主值Kx和Ky方向分别为x和y轴方向建立平面直角坐标系。假设间断面f1与y轴的夹角为β,间断面f2与y轴的夹角为α,忽略井筒形状的影响,则井点坐标为
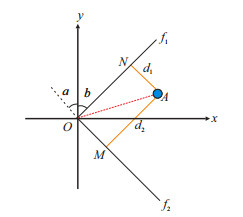 |
| 图1 变换前地层及井位分布图 Fig. 1 Distribution of formation and well location before transformation |
| $ \left( {{x_0}, {y_0}} \right) = \left[{\frac{{{d_2}\sin \beta + {d_1}\sin \left( {2\alpha } \right)}}{{\sin \left( {2\alpha + \beta } \right)}}, \frac{{{d_2}\cos \beta-{d_1}\cos \left( {2\alpha } \right)}}{{\sin \left( {2\alpha + \beta } \right)}}} \right] $ | (1) |
根据文献[1]采用如下坐标变换
| $ \left\{ {\begin{array}{*{20}{l}} {\xi = x/\sqrt \tau }\\ {\eta = y\sqrt \tau } \end{array}} \right. $ | (2) |
经变换以后,各向异性地层变为等价各向同性地层,如图 2所示。
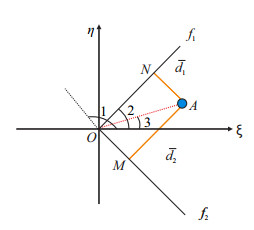 |
| 图2 变换后地层及井位分布图 Fig. 2 Distribution of formation and well location after transformation |
区域的渗透率变为
在新坐标系下OA的长度为
| $ {\bar d_0}\% = \frac{{\sqrt {{\tau ^2}{{\left[{{d_2}\cos \beta-{d_1}\cos \left( {2\alpha } \right)} \right]}^2} + {{\left[{{d_2}\sin \beta + {d_1}\sin \left( {2\alpha } \right)} \right]}^2}} }}{{\sin \left( {2\alpha + \beta } \right)\sqrt \tau }} $ | (3) |
OA与坐标轴ξ的夹角为
| $ {\gamma _3} = \arctan \left[{\tau \frac{{{d_2}\cos \beta-{d_1}\cos \left( {2\alpha } \right)}}{{{d_2}\sin \beta + {d_1}\sin \left( {2\alpha } \right)}}} \right] $ | (4) |
新坐标系下井点坐标为
| $ \left( {{\xi _0}, {\eta _0}} \right) = \left( {{{\bar d}_0}\cos {\gamma _3}, {{\bar d}_0}\sin {\gamma _3}} \right) $ | (5) |
井点到断面f1,f2距离分别为
| $ {\bar d_1} = \frac{{\left[{{d_2}\sin \beta + {d_1}\sin \left( {2\alpha } \right)} \right]\tan \beta }}{{\sin \left( {2\alpha + \beta } \right)\sqrt \tau \sqrt {{{\tan }^2}\beta + {\tau ^2}} }} -\\ \frac{{{\tau ^2}\left[{{d_2}\cos \beta-{d_1}\cos \left( {2\alpha } \right)} \right]}}{{\sin \left( {2\alpha + \beta } \right)\sqrt \tau \sqrt {{{\tan }^2}\beta + {\tau ^2}} }} $ | (6) |
| $ {\bar d_2} = \frac{{\left[{{d_2}\sin \beta + {d_1}\sin \left( {2\alpha } \right)} \right]\sqrt \tau \cot \alpha }}{{\sin \left( {2\alpha + \beta } \right)\sqrt {1 + {\tau ^2}{{\cot }^2}\alpha } }} +\\ {\rm{ }}\frac{{\sqrt \tau \left[{{d_2}\cos \beta-{d_1}\cos \left( {2\alpha } \right)} \right]}}{{\sin \left( {2\alpha + \beta } \right)\sqrt {1 + {\tau ^2}{{\cot }^2}\alpha } }} $ | (7) |
通过前文的坐标变换后,可将渗流模型等效为两夹角为
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\partial ^2}p}}{{\partial {r^2}}} + \frac{1}{r}\frac{{\partial p}}{{\partial r}}-\frac{{q\mu B\delta \left( {r-{{\bar d}_0}} \right)\delta \left( {\theta-{\gamma _3}} \right)}}{{Kh}} + }\\ {\frac{1}{{{r^2}}}\frac{{{\partial ^2}p}}{{\partial {\theta ^2}}} = \frac{{\mu \phi {c_{\rm{t}}}}}{K}\frac{{\partial p}}{{\partial t}}}\\ {p\left( {t = 0, \theta, r} \right) = {p_{\rm{e}}}}\\ {p\left( {t, \theta, r \to \infty } \right) = {p_{\rm{e}}}{\rm{;}}\frac{{\partial p\left( {t, \theta, r = 0} \right)}}{{\partial r}} = 0}\\ {\frac{{\partial p\left( {t, \theta = 0, r} \right)}}{{\partial \theta }} = 0{\rm{;}}\frac{{\partial p\left( {t, \theta = \omega, r} \right)}}{{\partial \theta }} = 0} \end{array}} \right. $ | (8) |
采用如下无因次化变形处理,
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\partial ^2}{p_{\rm{D}}}}}{{\partial r_{\rm{D}}^2}} + \frac{1}{{{r_{\rm{D}}}}}\frac{{\partial {p_{\rm{D}}}}}{{\partial {r_{\rm{D}}}}} + \frac{1}{{r_{\rm{D}}^2}}\frac{{{\partial ^2}{p_{\rm{D}}}}}{{\partial {\theta ^2}}} + }\\ {2{\rm{\pi }}\delta \left( {{r_{\rm{D}}}-{r_{{\rm{1D}}}}} \right)\delta \left( {\theta-{\gamma _3}} \right) = \frac{{\partial {p_{\rm{D}}}}}{{\partial {t_{\rm{D}}}}}}\\ {{p_{\rm{D}}}\left( {{t_{\rm{D}}} = 0, \theta, {r_{\rm{D}}}} \right) = 0}\\ {{p_{\rm{D}}}\left( {{t_{\rm{D}}}, \theta, {r_{\rm{D}}} \to \infty } \right) = 0}\\ {\frac{{\partial {p_{\rm{D}}}\left( {{t_{\rm{D}}}, \theta, {r_{\rm{D}}} = 0} \right)}}{{\partial {r_{\rm{D}}}}} = 0}\\ {\frac{{\partial {p_{\rm{D}}}\left( {{t_{\rm{D}}}, \theta = 0, {r_{\rm{D}}}} \right)}}{{\partial \theta }} = 0}\\ {\frac{{\partial {p_{\rm{D}}}\left( {{t_{\rm{D}}}, \theta = \omega, {r_{\rm{D}}}} \right)}}{{\partial \theta }} = 0} \end{array}} \right. $ | (9) |
采用有限差分方法计算模型。首先将网格进行剖分,rD方向剖分为N个网格,θ方向剖分为M 个网格,并采用如下变换:
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{1}{{{{\rm{e}}^{2{x_{\rm{D}}}}}}}\frac{{{\partial ^2}{p_{\rm{D}}}}}{{\partial x_{\rm{D}}^2}} + 2{\rm{\pi }}\delta \left( {{r_{\rm{D}}}-{r_{{\rm{1D}}}}} \right)\delta \left( {\theta-{\gamma _3}} \right) + }\\ {\frac{1}{{{{\rm{e}}^{2{x_{\rm{D}}}}}}}\frac{{{\partial ^2}{p_{\rm{D}}}}}{{\partial {\theta ^2}}} = \frac{{\partial {p_{\rm{D}}}}}{{\partial {t_{\rm{D}}}}}}\\ {{p_{\rm{D}}}\left( {{t_{\rm{D}}} = 0, \theta, {x_{\rm{D}}}} \right) = 0}\\ {{p_{\rm{D}}}\left( {{t_{\rm{D}}}, \theta, {x_{\rm{D}}} \to \infty } \right) = 0}\\ {\frac{{\partial {p_{\rm{D}}}\left( {{t_{\rm{D}}}, \theta, {x_{\rm{D}}} = 0} \right)}}{{\partial {x_{\rm{D}}}}} = 0}\\ {\frac{{\partial {p_{\rm{D}}}\left( {{t_{\rm{D}}}, \theta = 0, {x_{\rm{D}}}} \right)}}{{\partial \theta }} = 0}\\ {\frac{{\partial {p_{\rm{D}}}\left( {{t_{\rm{D}}}, \theta = \omega, {x_{\rm{D}}}} \right)}}{{\partial \theta }} = 0} \end{array}} \right. $ | (10) |
将方程组(10)离散化,得到离散方程为
| $ \frac{{p_{i + 1, j{\rm{D}}}^{n + 1}- 2p_{i, j{\rm{D}}}^{n + 1} + p_{i- 1, j{\rm{D}}}^{n + 1}}}{{\Delta x_{\rm{D}}^2}} + \\ \frac{{p_{i, j + 1{\rm{D}}}^{n + 1}- 2p_{i, j{\rm{D}}}^{n + 1} + p_{i, j - 1{\rm{D}}}^{n + 1}}}{{\Delta {\theta ^2}}} + \\ 2{\rm{\pi }}{{\rm{e}}^{2{x_{i{\rm{D}}}}}}\delta \left[{{x_{\rm{D}}}-\ln \left( {\frac{{{r_{{\rm{1D}}}}}}{{{r_{\rm{w}}}}}} \right)} \right]\delta \left( {\theta -{\gamma _3}} \right) = \\ {{\rm{e}}^{2{x_{i{\rm{D}}}}}}\frac{{p_{i, j{\rm{D}}}^{n + 1} -p_{i, j{\rm{D}}}^n}}{{\Delta {t_{\rm{D}}}}} $ | (11) |
将
| $ {a_{ij}}\delta {p_{i-1, j{\rm{D}}}} + {b_{ij}}\delta {p_{i, j-1{\rm{D}}}} + {c_{ij}}\delta {p_{i, j{\rm{D}}}} + {d_{ij}}\delta {p_{i, j + 1{\rm{D}}}} + {e_{ij}}\delta {p_{i + 1, j{\rm{D}}}} = {f_{ij}} $ | (12) |
其中
由于油井位置为(rD, γ3),则
在井点处
离散方程(12)可写成AδP=F的矩阵形式,其中A为M×N维五对角方阵;δP,F分别为M、N维列向量。该方程可采用高斯赛德尔迭代法求解,从而得到地层压力值。
2 实例计算与结果分析 2.1 实例计算国内某油田的一个断块埋深2 354~2 605 m,平均有效厚度7.5 m,x向、y向平均渗透率分别为115.9 mD和64.2 mD,平均孔隙度为20.5%,地层压力27.13 MPa,地层原油黏度10.4 mPa·s,原油密度0.855×103 kg/m3,原油体积系数1.051 m3/mm3,两断层夹角为50 °,生产井距两断层距离分别为50 m和31 m,生产井半径为0.12 m,产油量为14.64 m3/d。生产时间为100 d和300 d,计算地层压力等值线分布如图 3、4所示。
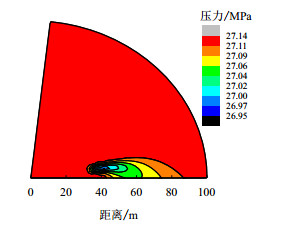 |
| 图3 生产100 d地层压力等值线图 Fig. 3 Contour map of pressure distribution at 100 d production |
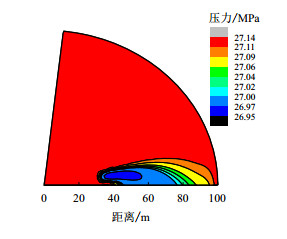 |
| 图4 生产300 d地层压力等值线图 Fig. 4 Contour map of pressure distribution at 300 d production |
由图 3和图 4可知,随着生产时间增加,压力波波及范围不断扩大,压力波波及区域地层压力迅速下降,生产井附近区域随生产时间增加而不断下降。压力波x方向波及速度大于y方向波及速度,这是因为地层x方向渗透率大于y方向渗透率。
2.2 断层夹角对油层压力影响对于不同断层夹角生产300 d地层压力等值线分布如图 5、图 6所示,油井井底压力随断层夹角变化如图 7所示。
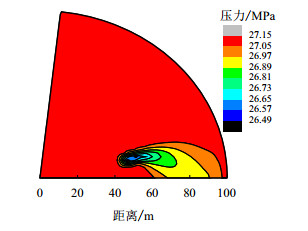 |
| 图5 40°夹角地层压力等值线图 Fig. 5 Contour map of pressure distribution of 40° angle |
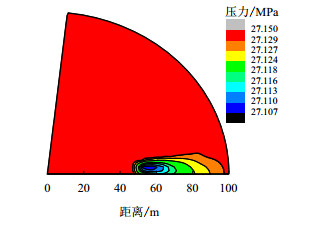 |
| 图6 60°夹角地层压力等值线图 Fig. 6 Contour map of pressure distribution of 60°angle |
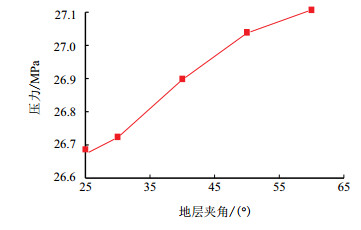 |
| 图7 井底压力随地层夹角变化曲线 Fig. 7 Relation between bottom hole pressure and formation angle |
由图 5、图 6可以看出,地层夹角越大,相同生产时间地层压降越小,压力值越高,压力波波及范围越大。主要原因是地层夹角越大,断层边界对油井生产影响越小,断层边界造成地层压降损失越小,从而地层压力值越大。从图 7可以看出,油井井底压力随地层夹角增大而增大。主要原因也由于断层夹角越大,断层对油井井底压力影响越小,油井压降损失越小。
2.3 渗透率各向异性对油井压力影响在平均渗透率
| 表1 不同渗透率各向异性系数下油井与断层距离 Table 1 The distance of oil well and cracks with different permeability anisotropic coefficients |
从表 1可以看出,随渗透率各向异性系数增加,油井与两断层之间距离的较小值先增大再减小。从图 8中看出井底压力随渗透率各向异性系数增大先增加再减小,即存在一个拐点,说明实际生产中存在最佳渗透率各向异性系数。
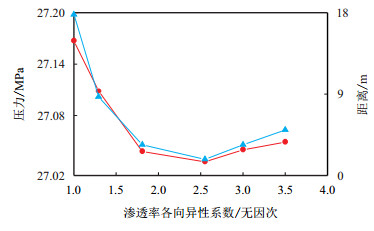 |
| 图8 井底压力随渗透率各向异性系数变化曲线 Fig. 8 Relation between bottom hole pressure and permeability anisotropic coefficient |
油井与断层距离随渗透率各向异性系数变化而变化,当油井与两断层之间距离的较小值减小,说明油井受到断层边界影响变大,从而导致油井压降损失增大;当油井与两断层之间距离的较小值增加,说明油井受到断层边界影响减小,从而导致油井压降损失减小。随着渗透率各向异性系数增加,油井与两断层之间距离的较小值先增大再减小,因而导致图 7中曲线出线拐点,即压降损失最大点。当渗透率各向异性系数大于拐点值后,油井压降损失减小,压力值升高。
3 结论(1) 由于各向异性油藏本身地质特征的复杂性,导致其开发中存在压力波波及速度在方向上存在差异,压力波在主渗透率方向上传播速度较大,地层压降更多发生在主渗透率方向上。
(2) 地层或油井井底压力随断层夹角不同发生变化。断层夹角越大,地层及油井压力值越高,反映出断层夹角越大,断层边界对生产影响越小。
(3) 渗透率各向异性系数不同,会导致油井与断层的最短距离发生改变,最终会导致油井井底发生改变。在文中计算实例中油井井底压力随渗透率各向异性系数增大呈现先减小后增大趋势。
符号说明f1,f2 —封闭断面;Kx,Ky — x向,y向渗透率,D;τ—渗透率各向异性系数,无因次;d1,d2 — xOy坐标系下生产井到两断面的距离,m;α,β—两断面与y轴的夹角,rad;x0 — xOy坐标系下井点横坐标,m;y0 — xOy坐标系下井点纵坐标,m;K —渗透率,D;γ1,γ2 —两断面与ξ轴的夹角,rad;γ —两断面间的夹角,rad;d0 —井点到坐标原点的距离,m;γ3—井点与坐标原点的连线和ξ轴的夹角,rad;ξ0 —ξOη坐标系下井点横坐标,m;η0 —ξOη坐标系下井点纵坐标,m;d1,d2 —ξOη坐标系下生产井到两断面的距离,m;p—压力,MPa;r —径向距离,m;θ —角度,rad;δ—狄拉克函数,无因次;q—单位面积产量,m3/(d·m2);B—原油体积系数,无因次;μ—原油黏度,mPa·s;h—油层厚度,m;φ—孔隙度,%;t —生产时间,h;ct —岩石压缩系数,MPa-1;pe —原始地层压力,MPa;rw —井眼半径,m;tD —无因次时间,无因次;rD —无因次井眼半径,无因次;r1D —无因次距离,无因次;pD —无因次压力,无因次;M、N —等分数,无因次;n—迭代时间步;下标i,j—沿坐标等分点计数。
| [1] |
周路, 王丽君, 罗晓容, 等. 断层连通概率计算及其应用[J].
西南石油大学学报:自然科学版, 2010, 32 (3) : 11 –18.
Zhou Lu, Wang Lijun, Luo Xiaorong, et al. The calculation application of fault connective probability[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2010, 32 (3) : 11 –18. |
| [2] |
刘宇, 李娜, 王涛. 断层的准确定位方法[J].
断块油气田, 2012, 19 (3) : 294 –296.
Liu Yu, Li Na, Wang Tao. Research on determining method of fault location[J]. Fault-block Oil & Gas Field, 2012, 19 (3) : 294 –296. |
| [3] | 卢德唐, 孔祥言. 扇形区域内有井储和表皮的井底压力[J]. 油气井测试, 1996, 5 (2) : 5 –10. |
| [4] | 王晓冬, 穆立婷. 两任意夹角断层的井壁压力计算方法[J]. 油气井测试, 1997, 6 (2) : 10 –12. |
| [5] | 刘月田, 王世军, 彭道贵. 非均质各向异性对地层渗流及油井产能的影响[J]. 西南石油学院学报, 2005, 27 (6) : 38 –41. |
| [6] | 刘月田. 各向异性油藏水平井渗流和产能分析[J]. 中国石油大学学报:自然科学版, 2002, 26 (4) : 40 –47. |
| [7] |
范乐宾, 刘月田, 顾少华, 等. 油藏各向异性对鱼骨井结构影响的数值模拟研究[J].
石油钻探技术, 2011, 39 (5) : 68 –73.
Fan Lebin, Liu Yuetian, Gu Shaohua, et al. Numerical study of the effect of reservoir anisotropy on fishbone well structure[J]. Petroleum Drilling Techniques, 2011, 39 (5) : 68 –73. |
| [8] |
刘月田. 各向异性油藏注水开发布井理论与方法[J].
石油勘探与开发, 2005, 32 (5) : 101 –104.
Liu Yuetian. Well location in water-flooding anisotropic oil reservoirs[J]. Petroleum Exploration and Development, 2005, 32 (5) : 101 –104. |
| [9] | 刘月田. 各向异性油藏水平井开发井网设计方法[J]. 石油勘探与开发, 2008, 35 (5) : 619 –624. |
| [10] | 刘月田, 葛家理. 各向异性圆形地层渗流的解析解[J]. 中国石油大学学报:自然科学版, 2000, 24 (2) : 40 –43. |
| [11] |
王海静, 薛世峰, 高存法. 各向异性油藏大斜度井入流动态[J].
石油勘探与开发, 2012, 39 (2) : 222 –227.
Wang Haijing, Xue Shifeng, Gao Cunfa. Inflow performance for highly deviated wells in anisotropic reservoirs[J]. Petroleum Exploration and Development, 2012, 39 (2) : 222 –227. |
| [12] |
王海静, 薛世峰, 高存法. 非均质各向异性油藏水平井流入动态[J].
大庆石油学院学报, 2012, 36 (3) : 79 –85.
Wang Haijing, Xue Shifeng, Gao Cunfa. Inflow performance for horizontal wells in heterogeneous, anisotropic reservoirs[J]. Journal of Daqing Petroleum Institute, 2012, 36 (3) : 79 –85. |
| [13] |
王大为, 李晓平. 各向异性油藏水平井产量公式校正方法研究[J].
西南石油大学学报:自然科学版, 2010, 32 (3) : 127 –131.
Wang Dawei, Li Xiaoping. Research on correction methods for horizontal well productivity formula in anisotropic reservoirs[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2010, 32 (3) : 127 –131. |
| [14] |
何志雄, 何家欢, 刘忠群, 等. 考虑各向异性的水平气井产能分析[J].
钻采工艺, 2010, 33 (6) : 43 –45.
He Zhixiong, He Jiahuan, Liu Zhongqun, et al. Deliverability analysis of horizontal gas well considering anisotropism[J]. Drilling & Production Technology, 2010, 33 (6) : 43 –45. |
| [15] | 陈元千, 郭二鹏. 对Joshi各向异性水平井产量公式的质疑、推导与对比[J]. 新疆石油地质, 2008, 29 (3) : 331 –334. |
 2015, Vol. 37
2015, Vol. 37


