2. 中国石油长城钻探工程公司地质研究院, 辽宁 盘锦 124010;
3. 中国石油塔里木油田公司开发事业部, 新疆 库尔勒 841000;
4. 中国石油长城钻探工程公司测试公司, 北京 朝阳 100101
2. CNPC Greatwall Drilling Company Geology Research Institute, Panjing, Liaoning 124010, China;
3. Development Department of Tarim Oilfield Company, PetroChina, Korla, Xinjiang 841000, China;
4. Well Testing Department of CNPC Greatwall Drilling Company, Chaoyang, Beijing 100101, China
对于产液量变化规律的研究,传统的做法是以经典的水驱特征曲线为基础,结合产油量预测模型来预测产液量的变化规律,国内外的学者在这方面做了很多的研究[1-5]。万新德研究了注聚后水驱油藏含水变化规律方面的研究[3];周学民在充分分析油田措施效果和潜力的基础上,研究了结构调整条件下油田产液量的变化趋势[4];胡建国提出一些预测产量的新模型[5];陈元千在这方面进行了比较深入的研究,主要成果有:1997年提出甲型水驱特征曲线与威布尔模型相结合来预测水驱开发指标[6],1998年提出丙型水驱特征曲线与威布尔模型结合和丙型水驱特征曲线与HCZ预测模型相结合的方法[7-8],1999年提出甲、丙型水驱特征曲线与广义翁式模型相结合的方法[9],而后于2000年提出乙型水驱特征曲线与威布尔模型相结合的方法[10],又于2001年提出甲、乙、丙型水驱特征曲线与Hubbert预测模型相结合来研究水驱开发指标的思路[11]。另外,景爱霞的研究思路是针对不同类型的油藏产液量的变化规律[12];韩军针对大庆葡萄花油田研究了高含水期的开发技术界限[13]。另外,国内外其他专家和学者也在这方面做过比较深入的研究[14-17]。
总的来看,这些方法在不同的生产区块具有各自的优势。然而,它们大多数的预测结果都是生产制度不变时的水驱开发指标。在油田的实际生产过程中,其生产制度经常会发生改变。本文给出了不同生产制度下产液量的变化规律,便于油田作业者根据油田的实际情况来采取相应的调整措施,为油田的高效开发提供了强有力的理论依据。
1 稳产时产液量的变化规律研究区域位于东部某油田北部背斜构造西部,构造比较平缓。开采面积为17.24 km2,地质储量12 937×104 t,其中,水驱地质储量8 215×104 t。多位专家和学者的研究结果表明,该高含水期该区块的水驱特征符合丙型水驱特征曲线。
油田在生产过程中,如果能够无限度地提高产液量,就可以保持油田稳产。在油田的后续生产中,如果没有重大的调整措施,水驱特征曲线的形式是不会发生改变的。这里可以假定一个生产区块定产油量生产,进而得到年产液量随时间的变化情况。假设生产区块以Qo=R定产量进行生产,对两边积分,有
| $ \int_0^t {{Q_{\rm{o}}}} {\rm{d}}t = \int_0^t {R{\rm{d}}t} $ | (1) |
由生产时间和累积产量的关系,式(1)可写成
| $ \int_{{N_{{\rm{pi}}}}}^{{N_{\rm{p}}}} {{\rm{d}}{N_{\rm{p}}}} = \int_0^t {R{\rm{d}}t} $ | (2) |
从而得到
| $ {N_{\rm{p}}} = {N_{{\rm{pi}}}} + Rt $ | (3) |
由水驱曲线关系Lp/Np=a+bLp,最终得到累积产液量随时间的变化
| $ {L_{\rm{p}}} = \frac{{a({N_{{\rm{pi}}}} + Rt)}}{{1 - b({N_{{\rm{pi}}}} + Rt)}} $ | (4) |
两边求导,略去生产关系代入过程,整理后得到年产液量随时间的变化
| $ {Q_{\rm{l}}} = \frac{{aR}}{{{{(1 - b{N_{{\rm{pi}}}} - bRt)}^2}}} $ | (5) |
以研究区域的某一区块为例,假设区块以年产油量36.13×104 t(2013年的产油量)的生产能力进行生产。如果没有重大的调整措施,按油田实际情况a=1.41,b=0.000 197。由生产动态知,到2013年的累积产油量为3 378.261×104 t。把2013年作为第1年,产液量随时间的变化如图 1所示。
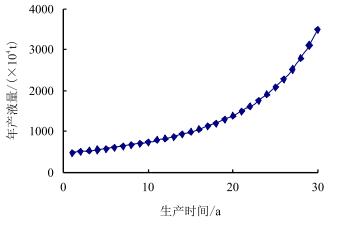 |
| 图1 年产液量变化规律 Fig. 1 The change of yearly liquid production |
从图 1中可以看出,要保持油田稳产,随着生产时间越长,需要产出的液量将越多。当再生产30 a后,产液量将会是目前的7倍,油田的生产工艺很难满足这种要求,所以定产生产是行不通的。
2 定产液量生产时产油量的变化规律假设区块以QL=κ定产液量进行生产,按照前面类似的推导过程,可以得到累积产油量随时间的变化和年产油量随时间的变化
| $ {N_{\rm{p}}} = \frac{{\kappa t + {L_{{\rm{pi}}}}}}{{a + b\left( {\kappa t + {L_{{\rm{pi}}}}} \right)}} $ | (6) |
| $ {Q_{\rm{o}}} = \frac{{a\kappa }}{{{{\left( {a + b\kappa t + b{L_{{\rm{pi}}}}} \right)}^2}}} $ | (7) |
以同一区块为例,假设区块以年产液量603.37×104 t(2013年的产液量)的生产能力进行生产。如果没有重大的调整措施,水驱特征曲线将不会改变,a=1.41,b=0.000 197。由生产动态知,到2013年的累积产液量为16 872.32×104 t。把2013年作为第1年,产油量随时间的变化如图 2所示。
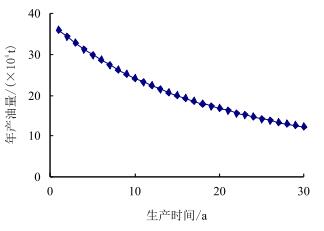 |
| 图2 年产油量变化规律 Fig. 2 The change of yearly oil production |
从图 2中可以看出,在这种工作制度下进行生产,生产20 a以后,年产油量不足20.00×104 t,不能很好的满足油田生产的要求。
3 产油量以一定速度递减时产液量的变化规律一般而言,在油田生产的中后期,要使产油量不变是不可能的。所以,必须让产量以一定的递减率生产。不同的递减率,产液量随时间的变化是不同的。产液量随时间变化的关系式的推导如下:年产油量随时间的变化为
| $ {Q_{\rm{o}}} = {Q_{{\rm{oi}}}}{(1 - k)^t} $ | (8) |
对式(8)两边积分
| $ \int_0^t {{Q_{\rm{o}}}} {\rm{d}}t = \int_o^t {{Q_{{\rm{oi}}}}} {(1 - k)^t}{\rm{d}}t $ | (9) |
由生产时间和累积产量的关系,式(9)可化为
| $ \int_{{N_{{\rm{pi}}}}}^{{N_{\rm{p}}}} {{\rm{d}}{N_{\rm{p}}}} = {Q_{{\rm{oi}}}}\left[{\frac{{{{\left( {1-k} \right)}^t}-1}}{{\ln \left( {1-k} \right)}}} \right] $ | (10) |
得到累积产油量的表达式为
| $ {N_{\rm{p}}} = {N_{{\rm{pi}}}} + {Q_{{\rm{oi}}}}\left[{\frac{{{{\left( {1-k} \right)}^t}-1}}{{\ln \left( {1-k} \right)}}} \right] $ | (11) |
将丙型水驱特征曲线的变形为
| $ {N_{\rm{p}}} = \frac{{1 - \sqrt {a(1 - {f_{\rm{w}}})} }}{b} $ | (12) |
进而得到
| $ 1 - {f_{\rm{w}}} = \frac{{{{\left( {1 - b{N_p}} \right)}^2}}}{a} $ | (13) |
最终得到产液量的表达式为
| $ \begin{array}{l} {Q_{\rm{l}}} = \frac{{{Q_{\rm{o}}}}}{{1 - {f_{\rm{w}}}}} = \frac{{a{Q_{\rm{o}}}}}{{{{(1 - b{N_{\rm{p}}})}^2}}} = \\ \;\;\;\;\frac{{a{Q_{{\rm{oi}}}}{{(1 - k)}^t}}}{{{{\left[{1-b\left( {{N_{{\rm{pi}}}} + {Q_{{\rm{oi}}}}\frac{{{{(1-k)}^t}-1}}{{\ln (1 - k)}}} \right)} \right]}^2}}} \end{array} $ | (14) |
仍然以同一区块为例,其他的假设与定产生产时相同。当油田分别以2%、4%、6%,8%的年递减率生产时,产液量的变化如图 3所示。
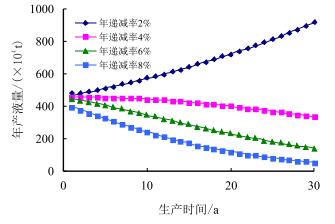 |
| 图3 年产液量变化规律 Fig. 3 The change of yearly oil production |
从图 3中可以看出,当油田的生产以一定的速度递减时,在刚开始生产的几年里,产液量的差异不是很大。但是,随着生产时间的延长,年递减率越小,产液量越大。而且,随着生产时间的延长,多产油的难度越来越大。因此,油田在生产的中后期,应综合考虑各方面的因素,力争以一个最合理的速度递减,保证油田取得较好的经济效益。
4 控制产液量的调整措施在油田生产的高含水期,要解决的问题有两个:一是减缓产油量的递减;二是抑制含水率的上升。而在实际生产中,要保证产油量几乎不递减,其含水率就会上升较快,可见这两个问题之间是矛盾的。因此,在解决这个问题的时候,应该从以下两个方面着手。
(1)寻找最佳的递减率
由前面的分析可知,不同的递减率其产液量是不同的。而油田的生产设备及生产成本又对其产液量有一定的限制。因此,应该根据区块的实际情况去选择一个合适的递减率以保证油田在最大效益的前提下开采。
(2)尽力采取能够“稳油控水”的措施
国内外多年的开采实践表明,各油田或生产区块一般会采取以下几个方面的调整措施。
①对于出水严重的井采取相应的堵水作业。在特高含水期,油井的含水率普遍比较高。对油井进行堵水,一般有两种方法:一种是利用封隔器等专门的堵水工具进行堵水,称之为机械堵水;另一种是利用注入的化学剂进行堵水作业,称之为化学堵水。油井进行堵水以后,不仅可以显著地降低油井的产液量,而且还可以起到増油的效果。
②对于吸水层非均质性比较严重的注入井,应该采取相应的调剖措施。当注入水进入非均质性比较严重的地层以后,一般会出现指进现象,即注入水沿着渗透率高的地层首先进入油井中,在这种情况下,不但会使油井过早见水,而且还使注入水不能很好地波及到物性较差的储层,降低了注入水的波及系数。如果采取合适的调剖措施,既可以减少水的指进,又可以提高油田的采收率,最终达到“稳油控水”的效果。
③对开发区块进行注采系统调整。调整注采系统时,可从以下3个角度考虑:一是调整注采井网的形式,如九点法面积注水与五点法面积注水的转换;二是缩小开发区块的井距,在必要的时候可以在薄差油层中布井,以提高可采储量的控制程度;三是进一步完善开发区块的注采系统,适当地补钻注水井或采油井,避免“有注无采”或“有采无注”的现象出现。
④在可以实施周期注水的开发区快实行周期注水。周期注水利用原有的井网和开发层系通过改变区域的压力场,进而来提高油田的采收率。因此,这种工艺措施的成本相对较低,在条件允许的情况下也可以大力推广。
5 结语在油田的实际生产中,定产液量生产不能满足油田生产的需求;而且油田的工艺措施不能满足其进行定产油量生产。因此,油田在生产的中后期,应综合考虑各方面的因素,力争以一个最合理的速度递减,保证油田取得较好的经济效益。
符号说明
Qo-年产油量, ×104 t;
R-年定产油量, ×104 t;
Ql-年产液量, ×104 t;
Np-累积产油量, ×104 t;
Npi-初始累积产油量, ×104 t;
Lp-累积产液量, ×104 t;
t-生产时间, a;
a, b-采取措施后新型特征曲线的特征系数, 无因次;
κ-年定产液量, ×104 t;
Lpi-最初的累积产液量, ×104 t;
k-年递减率,无因次;
Qoi-初始年产油量, ×104 t;
fw-含水率, %;
| [1] | Blasingame T A, McCray T L, Lee W J. Decline curve analysis for variable pressure drop/variable flowrate systems[C]. SPE 21513, 1991. http://www.pe.tamu.edu/blasingame/data/0_TAB_Public/TAB_Publications/SPE_021513_(MCcray)_Decl_Curve_An_for%20Var_Pressure_Drop_Var_Flowrate.pdf |
| [2] | Timmerman E H. Petroleum Engineering[M]. New York: Academic Pr, 1971 : 77 -78. |
| [3] |
万新德. 注聚后水驱油藏含水变化规律研究[J].
大庆石油地质与开发, 1986, 12 (5) : 37 –44.
Wan Xinde. Study on water cut change of water drive oil reserves after polymer flooding[J]. Petroleum Geology & Oilfield Development in Daqing, 1986, 12 (5) : 37 –44. |
| [4] |
周学民, 任玉林, 王者琴. 高含水后期油田产液量变化趋势研究[J].
石油勘探与开发, 1994, 21 (1) : 95 –98.
Zhou Xuemin, Ren Yulin, Wang Zheqin. A study of the variation of total liquid production of an oil field in its later high water cut stage[J]. Petroleum Exploration and Development, 1994, 21 (1) : 95 –98. |
| [5] |
胡建国, 陈元千, 张盛宗. 预测油气田产量的新模型[J].
石油学报, 1995, 16 (1) : 79 –86.
Hu Jianguo, Chen Yuanqian, Zhang Shengzong. A new model to predict production rate of oil and gas fields[J]. Acta Petrolei Sinica, 1995, 16 (1) : 79 –86. |
| [6] |
陈元千. 预测水驱油田开发指标及可采储量的联解法[J].
新疆石油地质, 1997, 18 (2) : 147 –152.
Chen Yuanqian. Combined solution for forecasting water drive development index and recoverable reserve[J]. Xinjiang Petroleum Geology, 1997, 18 (2) : 147 –152. |
| [7] |
陈元千. 水驱油田开发指标的预测方法[J].
断块油气田, 1998, 5 (3) : 29 –33.
Chen Yuanqian. The forecasting method of development indexes in water-drive oil field[J]. Fault-block Oil & Gas Field, 1998, 5 (3) : 29 –33. |
| [8] |
陈元千. 预测水驱油田开发动态的一种方法[J].
石油勘探与开发, 1998, 25 (1) : 43 –46.
Chen Yuanqian. A method for forecasting development performance of water drive oil field[J]. Petroleum Exploration and Development, 1998, 25 (1) : 43 –46. |
| [9] |
陈元千. 广义翁氏模型与水驱曲线的联解法[J].
新疆石油地质, 1999, 20 (2) : 134 –140.
Chen Yuanqian. Combined solution of generalized Weng model and water drive curve[J]. Xinjiang Petroleum Geology, 1999, 20 (2) : 134 –140. |
| [10] |
陈元千, 赵庆飞. Weibull预测模型与乙型水驱曲线的联解法[J].
新疆石油地质, 2000, 21 (5) : 405 –407.
Chen Yuanqian, Zhao Qingfei. Combined solution of generalized Weibull model and B water drive curve[J]. Xinjiang Petroleum Geology, 2000, 21 (5) : 405 –407. |
| [11] |
陈元千, 赵庆飞. Hubbert模型与水驱曲线联解法[J].
中国海上油气(地质), 2001, 15 (3) : 194 –198.
Chen Yuanqian, Zhao Qingfei. Combined solution of generalized Hubbert model and B water drive curve[J]. China Offshore Oil and Gas(Geology), 2001, 15 (3) : 194 –198. |
| [12] |
景爱霞. 不同类型油藏产液量变化规律分析及趋势[J].
江汉石油学院学报, 2003, 25 (5) : 82 –85.
Jing Aixia. Research on fluid production variation analysis and trend prediction about different types of reservoir[J]. Journal of Jianghan Petroleum Institute, 2003, 25 (5) : 82 –85. |
| [13] |
韩军, 侯君, 薛宗浩, 等. 葡萄花油田高含水期开发技术政策界限研究[J].
西安石油大学学报:自然科学版, 2004, 1 (5) : 44 –48.
Han Jun, Hou Jun, Xue Zonghao, et al. Research on development technology policy limit in high water-cut stage in Potaohua oilfield[J]. Journal of Xi'an Shiyou University:Natural Science Edition, 2004, 1 (5) : 44 –48. |
| [14] |
刘美佳, 宋考平, 张建国. 一种预测聚合物驱含水率及可采储量的简单方法[J].
石油钻探技术, 2007, 35 (5) : 98 –100.
Liu Meijia, Song Kaoping, Zhang Jianguo. A simple method to predict water cut and recoverable reserves in polymer flooding[J]. Petroleum Drilling Techniques, 2007, 35 (5) : 98 –100. |
| [15] |
刘朝霞, 韩冬, 王强. 一种预测聚合物驱含水率的新模型[J].
石油学报, 2009, 30 (6) : 903 –906.
Liu Zhaoxia, Han Dong, Wang Qiang. A new model for water cut prediction in polymer flooding[J]. Acta Petrolei Sinica, 2009, 30 (6) : 903 –906. |
| [16] |
吴书成, 刘明, 王云献, 等. 通过注水受效分析优化油井产液量[J].
新疆石油地质, 2010, 31 (2) : 178 –180.
Wu Shucheng, Liu Ming, Wang Yunxian, et al. Mass production optimization based on analysis of water flood response[J]. Xinjiang Petroleum Geology, 2010, 31 (2) : 178 –180. |
| [17] |
刘欢乐, 吴则鑫, 张博, 等. 油田生产制度改变时产液量变化规律预测[J].
石油钻探技术, 2013, 41 (5) : 102 –105.
Liu Huanle, Wu Zexin, Zhang Bo, et al. Regularity forecast for liquid production change when changing production parameters[J]. Petroleum Drilling Techniques, 2013, 41 (5) : 102 –105. |
 2015, Vol. 37
2015, Vol. 37


