2. 兰州大学地质科学与矿产资源学院, 甘肃 兰州 730000;
3. 中国石油天然气勘探开发公司, 北京 西城 100034;
4. 中国石油长庆油田分公司生产运行处, 陕西 西安 710018
2. School of Earth Sciences, Lanzhou University, Lanzhou, Gansu 730000, China;
3. China National Oil-Gas Exploration & Development Corporation, Xicheng, Beijing 100034, China;
4. Operation Department of Changqing Oilfield Company, PetroChina, Xi'an, Shaanxi 710018, China
自1936年Schilthuis R J利用物质守恒原理,首先建立油藏的物质平衡方程式以来,它在油藏工程中得到了广泛的应用和发展[1]。该方程很久以来就被认为是油藏工程师解释和预测油藏动态的基本方法之一[2]。物质平衡方程应用所涉及的一系列复杂性都隐含在生产压力动态中,同时它的求解一般情况下也不需要确定油藏几何形态,因而油田实践中在应用一些更复杂的技术(如二维、三维油藏数值模拟技术)之前,往往先应用油藏物质平衡方程进行计算求取油藏基本参数如油藏原始地质储量和水体参数, 以及预测油藏动态等。当前在石油工程领域关于物质平衡计算的商业软件种类繁多,如Petex的MBAL、Weatherford的MatBal和Epic的Resbalance等,其计算成本往往较高。传统的物质平衡计算方法则常常需进行线性化处理后常需多次手工试算[3],计算效率较低,而采用非线性规划的方法来求解油藏物质平衡问题,可以在仅已知少数实测油藏压力以及生产数据的情况下,通过计算机自动求得较准确的油藏基本参数,同时求出水体平均压力变化情况以及水侵动态。
1 物质平衡方程油藏物质平衡方程描述了油藏条件下,油藏膨胀的体积连同孔隙体积的减小以及外来流体的侵入等于油藏条件下产出液体的总量。本文所涉及的算例其油藏驱动方式属于天然水驱油藏,对应的油藏物质平衡方程如下
| $ {N_{\rm{p}}}\left[{{B_{\rm{o}}} + \left( {{R_{\rm{p}}}-{R_{\rm{s}}}} \right){B_{\rm{g}}}} \right] = \\ N{B_{{\rm{oi}}}}\left[{\frac{{({B_{\rm{o}}}-{B_{{\rm{oi}}}}) + ({R_{{\rm{si}}}}-{R_{\rm{s}}}){B_{\rm{g}}}}}{{{B_{{\rm{oi}}}}}} + \frac{{{c_{\rm{w}}}{S_{{\rm{wc}}}} + {c_{\rm{f}}}}}{{1-{S_{{\rm{wc}}}}}}\Delta p} \right] + \\ \left( {{W_{\rm{e}}} -{W_{\rm{p}}}} \right){B_{\rm{w}}} $ | (1) |
水侵量计算是物质平衡方程中非常重要的一部分,有大量的文献描述水侵模型以及计算水侵量的方法[4-5],中国很多学者在该领域也进行了深入的研究和探索,针对不同水侵类型分别给出了求解算法[6],以及在最优化理论[7-8]、积分变换与数值反演[9-13]等理论基础上提出了一系列水侵量计算方法,而李传亮等基于油气藏生产动态数据提出了水侵量的矿场简易计算方法[14-16]。本文的相关计算是在Fetkovich水侵模型[5]的基础上,利用最优化理论来实现的。选择Fetkovich模型的原因有二:(1) Hurst和van Everdingen模型[5](为表示方便,下文中简写为H-V模型)需要知道水体形状和大小,而Fetkovich模型只需要知道水体大小,因此工程实践中更容易获取相关数据;(2) Fetkovich模型消除了H-V模型中每个时间步长的叠加解的复杂性,相关计算更简单。当然也可以使用更为严格的H-V模型,但这种模型在计算上需要付出更多计算机时而在精度上却没有明显提高,在产水量不精确的情况下尤为明显。
Fetkovich M J于1971年提出了水侵量的近似计算公式[5]。为了便于描述水侵过程,引入了流入动态方程并假设压力在原始油藏和水体边界处保持恒定,实际上,随着油藏的开采,油藏与水体边界处的压力不断发生变化,这时如果把油藏与水体边界的压力变化划分为几个有限的时间步长,就可以满足定压条件,从而可直接计算,避免了使用叠加方法。第n个时间步长的水侵量计算公式为[3]
| $ \Delta {W_{{\rm{e}}, n}} = \frac{{{W_{{\rm{ei}}}}}}{{{p_{\rm{i}}}}}\left( {{{\bar p}_{{\rm{a}}, n-1}}-{{\bar p}_n}} \right){\rm{ }}\left( {1-{{\rm{e}}^{ - J{p_{\rm{i}}}\Delta {t_n}/{W_{{\rm{ei}}}}}}} \right) $ | (2) |
| $ {\bar p_{{\rm{a, }}n{\rm{-1}}}} = {p_{\rm{i}}}\left( {1-{W_{\rm{e}}}_{, n-1}/{W_{{\rm{ei}}}}} \right) $ | (3) |
| $ {\bar p_n} = ({p_{n-1}} + {p_n})/2 $ | (4) |
问题的实质是把有“实测油藏压力”(p0, n)数据点对应的“计算油藏压力”(pn)求出之后,通过拟合实测油藏压力来实现求取地质储量N、水侵系数J以及最大水侵量Wei,阶段水侵量ΔWe及阶段累计水侵量We,问题转化为求解目标函数F(N, J, Wei)的最小值问题,它是一具有线性约束条件的非线性规划问题
| $ \min F(N, J, {W_{{\rm{ei}}}}) = \sum\limits_n {{{\left( {{p_n}-{p_{0, n}}} \right)}^2}} $ | (5) |
约束条件
N > 0,J ≥ 0,Wei ≥ 0。
求解非线性规划问题通常的解法是将约束问题转化为无约束问题求解[18-20],有很多较为成熟的算法,本文非线性规划求解具体实现的流程如图 1所示,实现的算法描述如下:
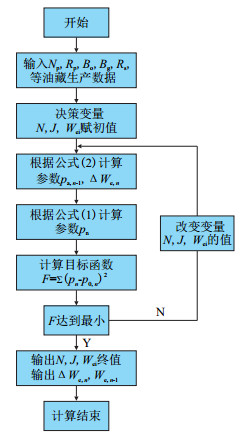 |
| 图1 规划求解计算流程图 Fig. 1 The calculating flow chart for programming solution |
(1) 根据给定的pi值以及J、Wei的初始估计值,得到N初值;
(2) 将式(5)设为规划求解最小值问题的目标函数,同时设定其对应的约束条件,即N > 0,J ≥ 0,Wei ≥ 0;
(3) 求解该非线性规划问题,当目标函数达到预先设定的精度时,生产数据的历史拟合过程完成,求解结束,此时预先估计的参数即N、J和Wei达到最佳估计值。然后根据式(2)可以确定每个时间步长的水侵量和相应的累计水侵量。
4 实例分析实例:某油藏[2],具有强天然水驱特征,该实例在多篇SPE文献中用作经典算例[21-23],油藏原始生产数据见表 1(部分原始数据进行了单位换算)。
| 表1 油藏生产数据 Table 1 Production data of the reservoir |
对表 1所示数据进行整理并通过式(1)、式(2)分别计算出“计算油藏压力”和每个时间步长的水侵量,然后利用规划求解对(pn -p0, n)2各项之和求最小值,最后求得拟合的计算结果。
最终计算该非线性规划的目标函数
| 表2 油藏基本参数计算结果对比分析 Table 2 Comparative analysis of calculation results of basic reservoir parameters |
| 表3 拟合过程中的油藏压力、水侵量计算 Table 3 Computation of reservoir pressure and water influx in fitting |
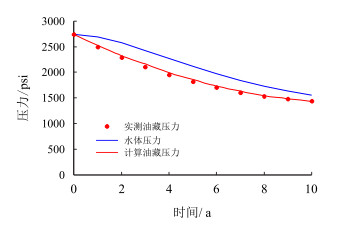 |
| 图2 压力拟合结果 Fig. 2 Fitting result of pressure |
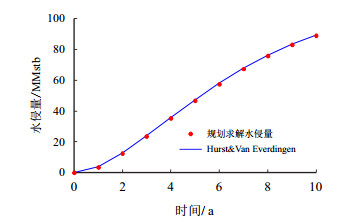 |
| 图3 水侵量计算结果对比 Fig. 3 Calculated results comparison of water flux |
由计算结果可知,“计算油藏压力”和“实测油藏压力”各时间步长相对误差的绝对值均小于3%(见表 3,图 2),计算水侵量同H-V模型计算结果也非常接近(图 3)。同时其他油藏参数(油藏地质储量、最大水侵量和水侵指数等)拟合计算结果也基本一致,其相对误差的绝对值均小于5%(表 2),这说明得到的计算结果是可靠的。
5 结语(1) 利用规划求解对一经典算例进行了基于非线性规划的物质平衡计算,求得了较准确的油藏基本参数油藏地质储量、最大水侵量和水侵指数,同时求出了水体平均压力变化情况以及水侵动态。
(2) 该方法相对于该领域的商业软件计算成本更低、计算过程更简单;相对于传统物质平衡计算不需要进行线性化处理和多次手工试算,在已知少数实测油藏压力以及生产数据的情况下,能自动求得较准确的油藏基本参数如原始地质储量和水体参数等,其可操作性强、计算方法可靠。
| [1] | 陈元千, 李璗. 现代油藏工程[M]. 北京: 石油工业出版社, 2004 : 88 -103. |
| [2] | Dake L P. Principles of reservoir engineering[M]. Elsevier Science, 1978 . |
| [3] | 李传亮. 油藏工程原理[M]. 北京: 石油工业出版社, 2005 : 133 -168. |
| [4] | van Everdingen A F, Hurst W. The Application of the laplace transformation to flow problems in reservoirs[J]. Trans. of AIME, 1949, 186 : 305 –325. |
| [5] | Fetkovitch M J. A simplified approach to water influx calculations-finite aquifer systems[J]. J. Pet. Tech., 1971 (7) : 814 –828. |
| [6] |
张继成, 白志威, 关春晓, 等. 天然水油藏水侵计算实用求解方法[J].
数学的实践与认识, 2011, 41 (19) : 82 –87.
Zhang Jicheng, Bai Zhiwei, Guan chunxiao, et al. A practical solution method for water encroachment calculation for a reservoir with natural water[J]. Mathematics in Practice and Theory, 2011, 41 (19) : 82 –87. |
| [7] |
王怒涛, 黄炳光, 张崇军, 等. 水驱气藏动态储量及水侵量计算新方法[J].
西南石油学院学报, 2000, 22 (4) : 26 –32.
Wang Nutao, Huang Bingguang, Zhang Congjun, et al. A novel method of calculating water-flooded gas in place and water influx of water drive gas reservoirs[J]. Journal of Southwest Petroleum Institute, 2000, 22 (4) : 26 –32. |
| [8] |
王怒涛, 陈浩, 张爱红, 等. 边底水油藏水侵量计算最优化方法[J].
大庆石油地质与开发, 2006, 25 (1) : 56 –58.
Wang Nutao, Chen Hao, Zhang Aihong, et al. Optimized method for calculating water influx rate of reservoir with edge and bottom water[J]. Petroleum Geology & Oil Field Development in Daqing, 2006, 25 (1) : 56 –58. |
| [9] |
廖运涛. 计算天然水侵量的回归公式[J].
石油勘探与开发, 1990 (1) : 71 –75.
Liao Yuntao. Regressive formula for calculating natural water influx rates[J]. Petroleum Exploration and Development, 1990 (1) : 71 –75. |
| [10] |
黄天星, 谢兴礼. 底水油藏无因次水侵量计算的数值反演法[J].
大庆石油地质与开发, 1994, 13 (4) : 32 –36.
Huang Tianxing, Xie Xingli. Numerical inversion algorithm for calculating dimensionless water influx rates from bottom water reservoir[J]. Petroleum Geology & Oil Field Development in Daqing, 1994, 13 (4) : 32 –36. |
| [11] |
张文中, 高春光, 李星民. 底水油藏确定水侵量的一种新方法[J].
新疆石油地质, 2006, 25 (6) : 62 –66.
Zhang Wenzhong, Gao Chunguang, Li Xingmin. A new method to determine water influx of reservoir with bottom water[J]. Xinjiang Petroleum Geology, 2006, 25 (6) : 62 –66. |
| [12] |
赵继勇, 胡建国, 凡哲元. 无因次水侵量计算新方法[J].
新疆石油地质, 2006, 27 (2) : 225 –228.
Zhao Jiyong, Hu Jianguo, Fan Zheyuan. A new method for calculating dimensionless water influx rate[J]. Xinjiang Petroleum Geology, 2006, 27 (2) : 225 –228. |
| [13] |
潘克家, 谭永基, 王才经. 自动识别油藏边界水侵量微分方程反演算法[J].
石油学报, 2008, 29 (5) : 747 –751.
Pan Kejia, Tan Yongji, Wang Caijing. Inversion algorithm of differential equation for automatically identifying water influx of reservoir boundary[J]. Acta Petolei Sinica, 2008, 29 (5) : 747 –751. |
| [14] |
李传亮. 气藏水侵量的计算方法研究[J].
新疆石油地质, 2003, 24 (3) : 430 –431.
Li Chuanliang. Determination of water influx in gas reservoirs[J]. Xinjiang Petroleum Geology, 2003, 24 (3) : 430 –431. |
| [15] |
李传亮, 仙立东. 油藏水侵量计算的简易新方法[J].
新疆石油地质, 2004, 25 (1) : 53 –57.
Li Chuanliang, Xian Lidong. Easy determination of water influx in reservoirs[J]. Xinjiang Petroleum Geology, 2004, 25 (1) : 53 –57. |
| [16] |
刘世常, 李闽, 巫扬, 等. 计算水驱气藏地质储量和水侵量的简便方法[J].
新疆石油地质, 2008, 29 (1) : 88 –90.
Liu Shichang, Li Min, Wu Yang, et al. Simple calculation of OGIP and water influx in gas pool by water drive process[J]. Xinjiang Petroleum Geology, 2008, 29 (1) : 88 –90. |
| [17] | 张光澄. 非线性最优化计算方法[M]. 北京: 高等教育出版社, 2005 . |
| [18] |
张长林, 余建星, 杨振国. 非线性约束最优化问题的多目标模拟退火算法[J].
复旦学报:自然科学版, 2003, 42 (1) : 93 –97.
Zhang Changlin, Yu Jianxing, Yang Zhenguo. The multiobject simulated annealing algorithm for the nonlinear constraint optimization problem[J]. Journal of Fudan University:Natural Science, 2003, 42 (1) : 93 –97. |
| [19] |
路晓伟, 蒋馥. 一种解决无约束非线性最优化问题的SD模型[J].
系统工程理论方法应用, 2003, 12 (1) : 64 –67.
Lu Xiaowei, Jiang Fu. A system dynamics model for solving nonlinear optimization problem without constraint[J]. Systems Engineering Theory Methodology Applications, 2003, 12 (1) : 64 –67. |
| [20] |
申合帅, 李泽民. 等式约束非线性最优化问题的一个降维算法[J].
山西师范大学学报:自然科学版, 2007, 21 (1) : 43 –47.
Shen Heshuai, Li Zemin. Descending dimension algorithm for nonlinear optimization problem with equality constraints[J]. Journal of Shanxi Normal University:Natural Science Edition, 2007, 21 (1) : 43 –47. |
| [21] | Hwan R R, Texaco Inc. Improved material balance calculations by coupling with a statistics-based historymatching program[C]. SPE 26244, 1993. |
| [22] | Ben Wang, Litvak B L, Bowman II G W. OILWAT:Microcomputer program for oil material balance with gas cap and water influx[C]. SPE 24437, 1992. |
| [23] | Yildiz T, Khosravi A. An analytical bottom water drive aquifer model for material balance analysis[C]. SPE 103283, 2006. |
 2015, Vol. 37
2015, Vol. 37


