2. "油气藏地质及开发工程"国家重点实验室·成都理工大学, 四川 成都 610059;
3. 成都理工大学"地球探测与信息技术"教育部重点实验室, 四川 成都 610059
2. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Chengdu University of Technology, Chengdu, Sichuan 610059, China;
3. Key Lab of Earth Exploration & Information Techniques of Ministry of Education, Chengdu University of Technology, Chengdu, Sichuan 610059, China
在油气地震勘探中,高信噪比和高分辨地震资料对于复杂地质构造的储层精细描述具有十分重要的意义,反褶积已成为提高地震资料分辨率的一种必要手段。目前,提高地震资料分辨率的方法有最小平方反褶积、预测反褶积、同态反褶积和最小熵反褶积等,这些反褶积方法都基于传统的Robinson褶积模型。在传统褶积模型中,地震信号的振幅随时间不发生改变。然而,地震波在地下介质中传播时,地下介质的黏弹性和非均质性将引起耗散效应和速度频散,即地震波会随着传播时间的延迟而发生振幅衰减和波形变形。因此,需要对传统褶积模型加以改进,建立更能反映地震波传播特性的动态褶积模型,并以此为理论基础,开展地震资料的反褶积处理,提高地震资料分辨率。
地层对地震波的吸收是引起地震子波时变的主要因素,地震资料的高分辨处理研究一直是热点问题之一,这方面的理论和方法可归纳为两大类。一类是时变反褶积方法,Robinson反褶积方法基于两种假设来实现[1],一是反射系数满足随机白噪的假定,据此假设可从地震道中估算子波振幅谱,二是假定子波为最小相位子波,这就允许子波相位谱可通过对估算的子波振幅谱求Hibert变换而获得。国内外诸多学者对此类反褶积方法作了大量的研究。Clarke[2]在最优化Wiener滤波基础上提出了时域非平稳反褶积方法。Koehler和Taner[3]提出了通用的时变反褶积数学理论方法。Rosa、赵波、孙成禹等提出了谱模拟反褶积方法[4-6],该方法假设子波振幅谱是光滑的,可用多项式在最小平方条件下拟合地震记录的振幅谱,并从中提取子波振幅谱,然后拓宽子波振幅谱的频带,达到提高分辨率的目的。唐博文等[6]在不使用多项式拟合并考虑反射系数颜色特征情况下实现了谱模拟反褶积的新方法。Margrave等提出了基于Gabor变换的时变反褶积处理方法[8-11],该方法能直接从地震记录的Gabor谱中直接估计衰减子波谱和反射系数谱。
另一类是反Q滤波方法:Hale[12]提出了基于Futterman[13]数学模型的反Q滤波,但该方法很难适用于大批量的数据计算。裴江云和何樵登[14]提出了基于Kjartansson[15]常Q模型的反Q滤波,该方法适用于非平稳地震数据的处理,能有效补偿振幅衰减和消除频散效应。众所周知,稳定性和计算效率是所有反Q滤波方法关注的重点。Wang[16-17]提出了基于波场延拓的反Q滤波方法,并将该稳定算法推广到Q随时间或深度连续变化的情况。Zhang和Ulrych[18]提出了基于最小平方和贝叶斯理论的反Q滤波方法,该方法能有效解决反Q滤波的稳定性问题。姚振兴等[19]根据地震波在非弹性介质中的传播规律提出了一种在深度域进行的反Q滤波方法。反Q滤波方法是目前进行地层吸收补偿的主要手段,该方法需要精确获得地层吸收的Q值,但在实际应用中Q值却无法精确求取,这就使得该方法在实际应用中受到限制。
地震勘探中,地震信号属于非平稳信号,由于不同频率的地震波具有不同的特点,因此,需要对不同频率的地震波采取不同的处理策略,而传统傅里叶变换无法对其进行全面分析。目前,许多地球物理学家在傅里叶变换基础上,提出并发展了一系列新的非平稳信号分析处理方法,如短时傅里叶变换[20]、Gabor变换[21]、小波变换[22]等。Stockwell于1996年提出S变换[23],它是一种线性、多分辨率、无损可逆的时频分析方法,综合了短时傅里叶变换和小波变换的优点且避免了它们的不足。由于S变换中基本小波函数形态固定,使其在实际应用中受到限制。为了克服这一局限,国内外诸多学者对S变换进行了改造和推广,提出了广义S变换[24-26],可以根据实际资料处理需要来灵活选择参数。
受Margrave[27]提出的基于Gabor变换的非平稳反褶积方法的启发,在动态褶积模型基础上,结合不同频率的地震波随时间有不同的吸收衰减特性,提出了一种基于广义S变换的动态反褶积方法,该方法将广义S变换良好的多分辨特性引入到地震资料动态反褶积处理中,其理论基础是将非平稳地震记录的广义S变换近似表示为静态震源子波的Fourier变换、复数值时频衰减函数与反射系数广义S变换的乘积。经理论模型分析和实际资料处理验证了该方法的正确性和适用性,能有效提高地震资料的分辨率。
1 方法原理 1.1 广义S变换设函数
| $ S\left( {\tau, f} \right) = \int_{- \infty }^{ + \infty } {x\left( t \right)} \frac{{\left| f \right|}}{{\sqrt {{\rm{2\pi }}} }}\exp \left[{-\frac{{{{\left( {\tau-t} \right)}^2}{f^2}}}{2}} \right]\exp \left( { -i2{\rm{\pi }}ft} \right)dt $ | (1) |
式中:τ—时间;τ—频率;L2 (R)—实数域中的平方可积函数空间。
S变换中基本小波函数定义为
| $ \begin{array}{l} {w_f}\left( t \right) = \frac{{\left| f \right|}}{{\sqrt {2{\rm{\pi }}} }}\exp \left( {\frac{{-{t^2}{f^2}}}{2}-i2{\rm{\pi }}ft} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;gf\left( t \right)\exp \left( {-i2{\rm{\pi }}ft} \right) \end{array} $ | (2) |
记高斯窗为
| $ gf\left( t \right) = \frac{{\left| f \right|}}{{\sqrt {2{\rm{\pi }}} }}\exp \left( {-\frac{{{t^2}{f^2}}}{2}} \right) $ | (3) |
对时间τ进行积分,则可得到x(t)的傅里叶谱X(f),即
| $ \int_{ - \infty }^{ + \infty } {S\left( {\tau ,f} \right){\rm{d}}\tau } = {\rm{X}}\left( {\rm{f}} \right) $ | (4) |
故反S变换定义为
| $ x\left( t \right) = \int_{-\infty }^{ + \infty } {\left\{ {\int_{-\infty }^{ + \infty } {S\left( {\tau, f} \right){\rm{d}}\tau } } \right\}\exp \left( {i2{\rm{\pi }}ft} \right){\rm{df}}} $ | (5) |
在S变换中,基本小波函数(式(2))由简谐波与Gaussian函数的乘积构成,简谐波在时间域仅作伸缩变换,而Gaussian函数则进行伸缩和平移,使得S变换中的基本变换函数形态固定,使其应用受到限制。若对高斯窗函数(式(3))进一步推广,定义
| $ gf\left( t \right) = \frac{{{{\left| f \right|}^r}}}{{\sigma \sqrt {2{\rm{\pi }}} }}\exp \left( {-\frac{{{t^2}{f^{2r}}}}{{2{\sigma ^2}}}} \right) $ | (6) |
联立式(1)、式(3)和式(6),则函数x(t)的广义S变换定义为
| $ S{\left( {\tau, f} \right)_G} = \int_{- \infty }^{ + \infty } {x\left( t \right)} \frac{{{{\left| f \right|}^r}}}{{\sqrt 2 {\rm{\pi }}\sigma }}\exp \left[{-\frac{{{{\left( {\tau-t} \right)}^2}{{\left| f \right|}^{2r}}}}{{2{\sigma ^2}}}} \right]\exp \left( { -i2{\rm{\pi }}ft} \right){\rm{dt}} $ | (7) |
式(7)即为扩展的广义S变换。
当r=0时,式(7)即为Gabor变换;当σ=1,r=1时,式(7)蜕化为S变换。由于在对实际地震资料进行处理时,不同区块的地震资料振幅谱和相位谱差异明显,故在选择参数r和σ时,应根据实际情况进行试验后灵活处理,才可以达到最佳的处理效果。
1.2 动态反褶积模型传统的褶积模型通常被认为是地震资料反褶积处理的基础,表示为
| $ {x_{{\rm{stat}}}}\left( t \right) = \omega \left( t \right) * r\left( t \right) = \int_{-\infty }^{ + \infty } {\omega \left( {t-\tau } \right)r\left( \tau \right){\rm{d}}\tau } $ | (8) |
即平稳地震记录xstat(t)为静态震源子波
由于该模型中的静态子波
| $ {x_{{\rm{nonstat}}}}\left( t \right) = \omega \left( {t, \tau } \right) * r\left( t \right) = \int_{-\infty }^{ + \infty } {\omega \left( {t-\tau, \tau } \right)r\left( \tau \right){\rm{d}}\tau } $ | (9) |
式(9)即为动态褶积模型[11],xnonstat(t)表示非平稳地震记录,当τ为常量时,则式(9)退化为静态褶积模型,它是动态褶积模型的一种特例,因此,用动态褶积模型来描述子波传播过程与实际情况更相符。
实际上,地震波在非均匀介质中传播时,由于地层的吸收作用,子波振幅会随时间和频率的变化而发生衰减,最终形成衰减地震道。在考虑地层黏滞特性的情况下,引入衰减函数α(t,f)来代表地震波的衰减效应,其傅里叶反变换为
| $ \alpha \left( {t, \tau } \right) = \int_{-\infty }^{ + \infty } {a\left( {t, f} \right)} \exp \left( {i2{\rm{\pi }}f\tau } \right){\rm{df}} $ | (10) |
在常Q衰减理论基础上,衰减函数α(t,f)的振幅谱可表示为[27]
| $ \left| {\alpha \left( {t, f} \right)} \right| = \exp \left( {{\rm{-\pi }}ft/Q} \right) $ | (11) |
在考虑地层吸收衰减的情况下,假定有一地层反射系数函数[r(t)],在脉冲源δ(t)的作用下,式(9)中的
| $ {x_{{\rm{nonstat}}}}\left( t \right) = \alpha \left( {\tau ,t} \right) * r\left( t \right) = \int_{ - \infty }^{ + \infty } {\alpha \left( {\tau ,t - \tau } \right)r\left( \tau \right){\rm{d}}\tau } $ | (12) |
在频率域,式(12)变为
| $ {{\hat x}_{{\rm{nonstat}}}}\left( f \right) = \int_{ - \infty }^{ + \infty } {\alpha \left( {t,f} \right)} r\left( t \right)\exp \left( { - 2{\rm{\pi }}ift} \right){\rm{dt}} $ | (13) |
式(13)可看作一种常Q模型的衰减脉冲响应,将脉冲源替换为静态震源子波,则式(13)可扩展为更通用的形式
| $ {{\hat x}_{{\rm{nonstat}}}}\left( f \right) = \omega \left( f \right)\int_{ - \infty }^{ + \infty } {\alpha \left( {t,f} \right)} r\left( t \right)\exp \left( { - 2{\rm{\pi }}ift} \right){\rm{dt}} $ | (14) |
式(14)是非平稳地震记录的傅里叶变换,由此可以得到它在S域中的近似表达式
| $ {V_{{\rm{GST}}}}{x_{{\rm{nonstat}}}}\left( {\tau, f} \right) \approx \omega \left( f \right)\alpha \left( {\tau, f} \right){V_{{\rm{GST}}}}r\left( {\tau, f} \right) $ | (15) |
式(15)表明:在t=τ时刻,非平稳地震记录xnonstat(t)的广义S变换VGSTxnonstat(τ,f)近似等同于静态震源子波
如果只考虑地震记录振幅谱,由式(15)可以得到非平稳地震记录动态褶积模型在S域中的另一表现形式
| $ \left| {{V_{{\rm{GST}}}}{x_{{\rm{nonstat}}}}\left( {\tau, f} \right)} \right| \approx \left| {\omega \left( f \right)} \right|\left| {\alpha \left( {\tau, f} \right)} \right|\left| {{V_{{\rm{GST}}}}r\left( {\tau, f} \right)} \right| $ | (16) |
式中:
由式(16)可知,非平稳地震记录的广义S变换时频谱值包含两个部分,一部分为反射系数时频谱值
(1)平滑地震记录时频谱值
假设地层反射系数具有随机白噪的统计特性,其频谱具有白谱特征,则可认为地震记录时频谱值的细节部分由反射系数引起,主要趋势由动态子波引起。本文采用Rosa[4]提出的用多项式在最小平方意义条件下拟合非平稳地震记录振幅谱的平滑方法,即广义S域中采用振幅谱模拟的方法来拟合动态子波谱,这与Margrave[11]提出在Gabor域中估算反射系数的方法有所不同。若地震记录时频谱值
| $ {\left| {{\omega _\alpha }\left( {\tau, f} \right)} \right|_{{\rm{est}}}} \cong {\left| {{V_{{\rm{GST}}}}{x_{{\rm{nonstat}}}}\left( {\tau, f} \right)} \right|_{{\rm{est}}}} $ | (17) |
(2)求反褶积因子
在求得估算的动态子波时频谱值
| $ \left| {A\left( {\tau, f} \right)} \right| \cong \frac{1}{{\left( {{{\left| {{\omega _\alpha }\left( {\tau, f} \right)} \right|}_{{\rm{est}}}} + \mu {A_{\max }}} \right)}} $ | (18) |
式(18)中:µ为一很小的正实数,Amax为
| $ \theta \left( {\tau, f} \right) = H\left\{ {\ln \left( {{{\left| {{\omega _\alpha }\left( {\tau, f} \right)} \right|}_{{\rm{est}}}} + \mu {A_{\max }}} \right)} \right\} $ | (19) |
式中:H表示希尔伯特变换,则反褶积因子为
| $ \begin{array}{l} A\left( {\tau, f} \right) = \left| {A\left( {\tau, f} \right)} \right|\exp \left[{-i\theta \left( {\tau, f} \right)} \right] = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{{\left( {{{\left| {{\omega _\alpha }\left( {\tau, f} \right)} \right|}_{{\rm{est}}}} + \mu {A_{\max }}} \right)}}\exp \left[{-i\theta \left( {\tau, f} \right)} \right] \end{array} $ | (20) |
(3)反褶积
在S域中将反褶积因子A(τ,f)与地震记录时频谱值VGSTxnonstat(τ,f)相乘,即可获得估计的时频域反射系数r(τ,f)est,再通过S反变换即可求得估计的时间域反射系数r(τ)est
| $ \begin{array}{l} r{\left( {\tau, f} \right)_{{\rm{est}}}} = \left| {r{{\left( {\tau, f} \right)}_{{\rm{est}}}}} \right|\exp \left[{-i\theta \left( {\tau, f} \right)} \right] = \;\;\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{V_{{\rm{GST}}}}{x_{{\rm{nonstat}}}}\left( {\tau, f} \right)}}{{\left( {{{\left| {{\omega _\alpha }\left( {\tau, f} \right)} \right|}_{{\rm{est}}}} + \mu {A_{\max }}} \right)}}\exp \left[{-i\theta \left( {\tau, f} \right)} \right] \end{array} $ | (21) |
为了验证地震资料在S域中的动态反褶积处理效果,现设计一理论模型来验证该方法的有效性和正确性。理论模型中采用50 Hz的雷克子波,首先,生成随机白噪序列作为地层的反射系数(图 1a),然后,使用式(8)中的静态褶积模型得到平稳合成地震记录(图 1c),合成记录显示,地震波振幅在传播过程中满足时不变性,信号能量和波形随时间延迟不发生改变。由于静态褶积模型没有考虑到非均匀介质对地震波的吸收衰减效应,现以式(9)中的动态褶积模型为基础,利用式(14)的傅里叶反变换可得到非平稳地震记录(图 1d),在0~0.5 s,衰减函数中品质因子Q=50,在0.5~1.2 s,Q=35,随传播时间的延迟,反射波地震信号振幅逐渐衰减,该衰减地震道不仅反映了地震波在传播过程中的时变性,还能更好地刻画地震波在黏弹性介质中的衰减效应和传播特性。图 1b是基于时频域动态反褶积方法估计得到的反射系数,即为动态反褶积结果,这里式(7)中高斯窗函数参数采用σ=5,r=0.7。比较实际反射系数(图 1a)和估计反射系数(图 1b)可以看出,二者整体形态比较相似,时间起跳点较为一致,随着时间的增大,估计的反射系数形态宽度比实际反射系数形态宽度略大,这是深层地震波振幅衰减剧烈导致的,但并不影响动态反褶积的整体效果。
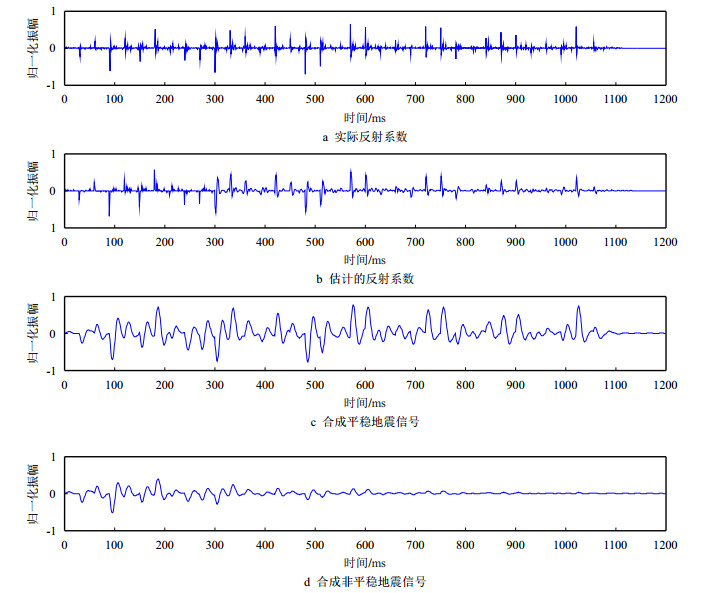 |
| 图1 合成地震记录动态反褶积结果 Fig. 1 The results of dynamic deconvolution for a synthetic |
图 2展示的是合成非平稳地震信号xnonstat(t)(图 1d)基于时频域动态反褶积方法的实施过程。首先,对图 1d中的衰减地震信号做广义S正变换,然后,求得时频谱|VGSTxnonstat(τ,f)|(图 2a),该图显示衰减地震信号的主频约为50 Hz,地震信号的振幅随时间和频率的增大逐渐衰减。由于预先假定反射系数序列具有随机白噪特性,故可通过式(17)对图 2a进行谱平滑来消除地层反射系数的影响,其平滑结果即为估计的动态子波时频谱
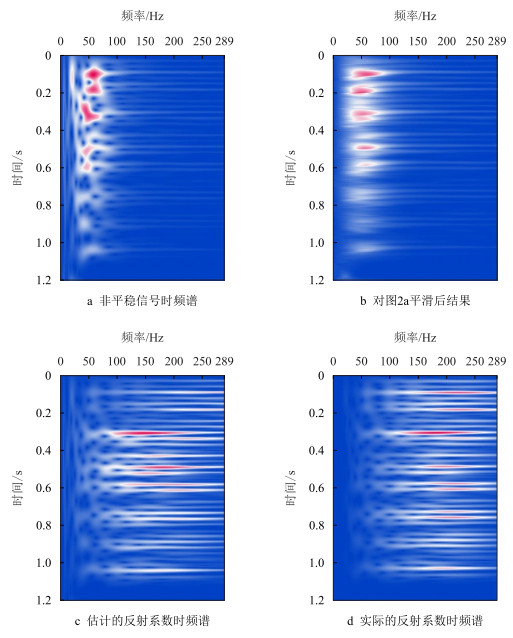 |
| 图2 不同信号的时频谱 Fig. 2 The time-frequency spectra of different signal |
为验证广义S域动态反褶积方法在实际资料处理中的可行性和稳定性,对中国西部A地区某实际三维工区原始叠加剖面进行反褶积处理。受地层吸收衰减的影响,该区资料中、深部地震信号振幅能量较弱,如原始叠加剖面(图 3a)中红色和黄色椭圆区域所示,地震剖面特征表现为厚层少,薄层多。在未进行高分辨处理之前,原始地震资料不能有效识别目的层反射波信息。图 3b是使用本文所述方法在S域中对该原始叠加剖面进行动态反褶积处理的结果,处理前后剖面对比表明:处理后的剖面同相轴得到有效压缩,剖面的分辨率明显提高,而资料的信噪比没有明显降低,能明显刻画出薄层致密砂岩反射信息(图 3b红色椭圆区域),表现为反射波同相轴变细、增多、地层接触关系良好的特点。同时,深部地震信号能量也得到有效补偿(图 3b黄色椭圆区域),断层断点清晰可见,剖面的成层性和连续性更好。
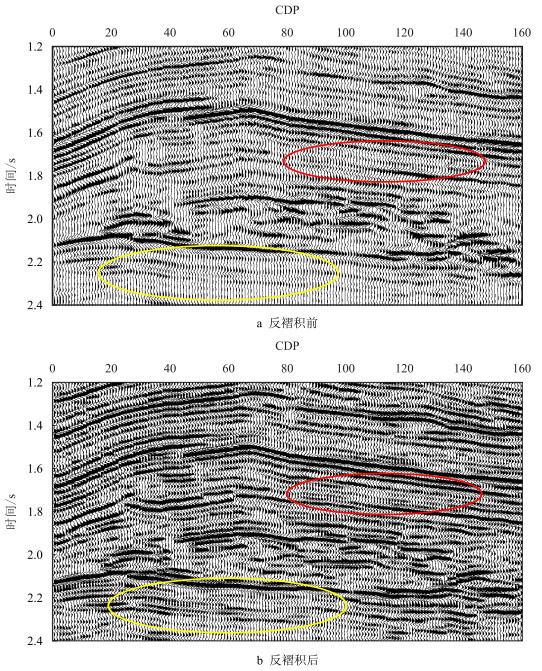 |
| 图3 时频域动态反褶积剖面对比 Fig. 3 The comparison of the dynamic deconvolution profile in time-frequency domain |
图 4是S域动态反褶积处理前后剖面第100道信号的时域对比图,即抽取图 3a中第100道地震信号,如图 4a所示,图 4b是动态反褶积处理后的结果。为了便于比较,对抽取的第100道信号进行了归一化处理。对比1.7~2.0 s处的信号发现,动态反褶积处理后的反射波信息明显增多,这对于薄层砂岩的识别有较大优势。为了获取资料处理前后地震信号的频率随时间变化特性,对图 4中的信号在S域中进行时频谱对比分析,得到动态反褶积前后第100道信号的时频谱对比结果(图 5)。
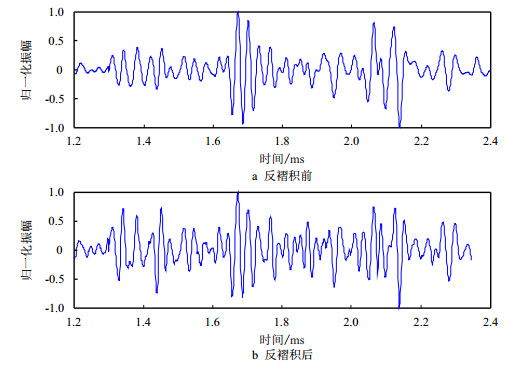 |
| 图4 图 3中第100道信号动态反褶积前后时域对比 Fig. 4 The comparison of the 100th signal in Figure 4 before and after deconvolution |
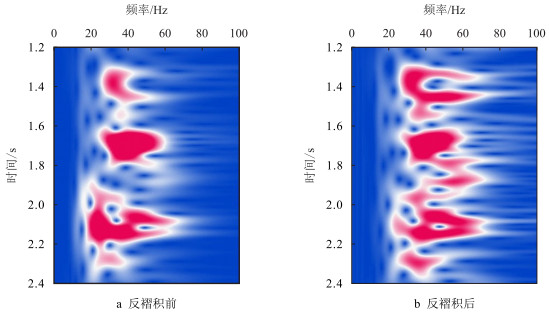 |
| 图5 动态反褶积前后剖面第100道信号时频谱对比 Fig. 5 The comparison of the time-frequency spectra for the 100th signal of Figure 4 before and after deconvolution |
图 5a是原始剖面中第100道信号的广义S谱,此处广义S变换时采用的高斯窗函数参数经实验选取(σ=5,r=0.7。对于该参数的选取问题,由于不同地区的地震资料差异较大和地震响应模式各异,故应根据实际情况在测井资料控制下通过实验来选取合理的参数)。从图 5a可以看出,原始资料的频带约10~50 Hz,主频约30 Hz,随着时间的延迟,高频信息衰减较为明显,主频重心向低频方向移动。图 5b是动态反褶积处理后信号的广义S谱,从图 5a和图 5b的时频谱对比可知,经本文方法处理后的地震信号频带宽约10~60 Hz,主频提高到约45 Hz,在保持低频信息变化较小的情况下,主频得到提高,频带得以展宽,同时,高频能量信息也得到有效补偿。因此,基于广义S变换的动态反褶积方法不仅能提高地震资料的分辨率,也能补偿由于大地吸收所引起的高频成分。
图 6a和图 7a是从三维原始资料抽取1 800 ms和2 000 ms时的时间切片,其岩性和构造特征较为杂乱,断点模糊(如图 6a黄色椭圆区域),难以直接识别和解释,地震信号能量随时间增大而逐渐衰减。对原始三维资料实施时频域动态反褶积处理,图 6b和图 7b是从处理后数据体中抽取的对应时间切片。处理前后的时间切片对比表明,处理后的资料品质明显提高,分辨率提高较大(如图 7b绿色椭圆所示区域),同时,横向连续性好,非均匀性亦清晰可辨,局部构造特征得以凸显,断点清晰可见(如图 6b中黄色椭圆区域所示),地层吸收引起的地震记录衰减能量也得到有效补偿。
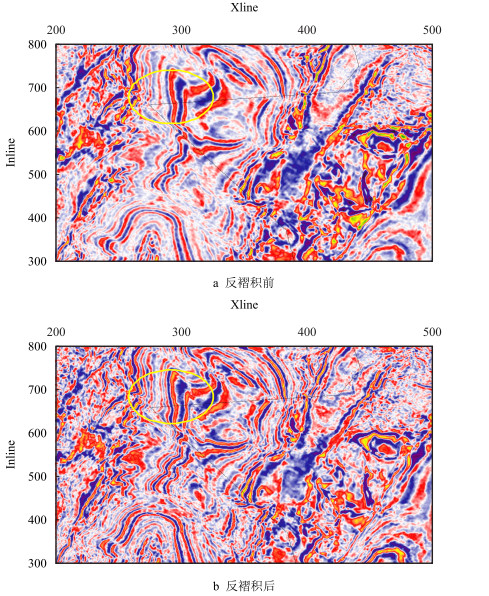 |
| 图6 动态反褶积前后第1 800 ms时间切片对比图 Fig. 6 The comparison of 1 800 ms time slice before and after deconvolution |
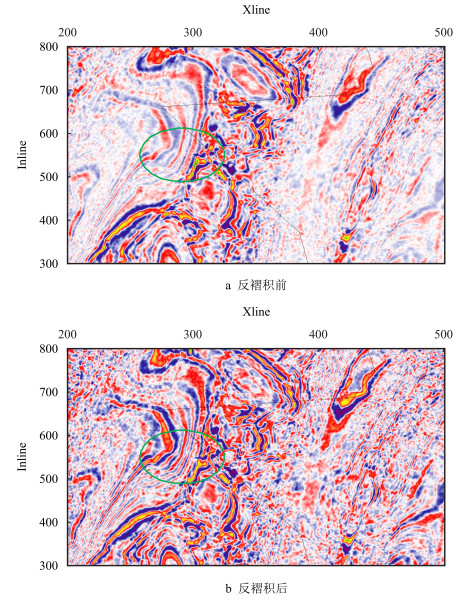 |
| 图7 动态反褶积前后第2 000 ms时间切片对比图 Fig. 7 The comparison of 2 000 ms time slice before and after deconvolution |
(1)由于广义S变换的多分辨率分析特性,且可保持频率和时间对应关系,因此可对原始地震资料进行多尺度分解,从而可在S域中实施地震资料动态反褶积处理,该方法在处理随时间、空间和频率发生变化地震信号时,具有良好的适用性。
(2)该方法不需要直接求取Q值且容易实现,且在进行大批量地震数据高分辨处理时,算法稳定性保持良好。
(3)S域动态反褶积处理后的叠后剖面在横向和纵向上保持了处理前剖面的整体形态和能量分布关系,地震记录分辨率明显改善,频带展宽,对弱反射层和薄层的分辨力得以加强,中、深部衰减的地震信号能量也得到有效补偿。
(4)由于估算的动态子波谱是在S域中对非地震道频谱进行平滑处理而获得,平滑函数的选取对处理效果有一定的影响,因此,频谱的计算方法和平滑方式有待进一步研究。
| [1] | Robinson E A, Treitel S. Principles of digital Wiener filtering[J]. Geophysical Prospecting, 1967, 15 (3) : 311 –332. DOI:10.1111/gpr.1967.15.issue-3 |
| [2] | Clarke G K C. Time-varying deconvolution filters[J]. Geophysics, 1968, 33 : 936 –944. DOI:10.1190/1.1439987 |
| [3] | Koehler F, Taner M T. The use of the conjugate-gradient algorithm in the computation of predictive deconvolution operators[J]. Geophysics, 1985, 50 : 2752 –2758. DOI:10.1190/1.1441895 |
| [4] | Rosa A L R. Processing via spectral modeling[J]. Geophysics, 1991, 56 (8) : 1244 –1251. DOI:10.1190/1.1443144 |
| [5] |
赵波, 俞寿朋, 聂勋碧, 等. 谱模拟反褶积及其应用[J].
石油地球物理勘探, 1996, 31 (1) : 101 –115.
Zhao Bo, Yu Shoupeng, Lie Xunbi, et al. Spectralmodeled deconvolution and its application[J]. Oil Geophysical Prospecting, 1996, 31 (1) : 101 –115. |
| [6] |
孙成禹. 谱模拟方法及其在提高地震资料分辨率中的应用[J].
石油地球物理勘探, 2000, 35 (12) : 27 –34.
Sun Chengyu. Spectrum modeling method and its application to seismic resolution improvement[J]. Oil Geophysical Prospecting, 2000, 35 (12) : 27 –34. |
| [7] |
唐博文, 赵波, 吴艳辉, 等. 一种实现谱模拟反褶积的新途径[J].
石油地球物理勘探, 2010, 45 (1) : 66 –70.
Tang Bowen, Zhao Bo, Wu Yanhui, et al. A new way to realize spectral modeling deconvolution[J]. Oil Geophysical Prospecting, 2010, 45 (1) : 66 –70. |
| [8] | Margrave G F, Lamoureux M P. Gabor deconvolution[R]. CREWES Research Report. 2001, 13:241-276 |
| [9] | Margrave G F, Lamoureux M P, Grossman J P, et al. Gabor deconvolution of seismic data for source waveform and Q correction[C]. 72th Annual International Meeting, SEG, Expanded Abstracts, 2002:2190-2193 |
| [10] | Montana C A, Margrave G F. Surface-consistent Gabor deconvolution[C]. 76th Annual International Meeting, SEG, Expanded Abstracts, 2006:2812-2816. |
| [11] | Margrave G F, Lamoureux M P, Henley D C. Gabor deconvolution:Estimating reflectivity by nonstationary deconvolution of seismic data[J]. Geophysics, 2011, 76 (3) : W15 –W30. DOI:10.1190/1.3560167 |
| [12] | Hale D. Q adaptive deconvolution[J]. Standford Exploration Projece, 1982, 30 : 133 –158. |
| [13] | Futterman W I. Dispersive body waves[J]. Journal of Geophysical Research, 1962, 67 (13) : 5279 –5291. DOI:10.1029/JZ067i013p05279 |
| [14] |
裴江云, 何樵登. 基于Kjartansson模型的反Q滤波[J].
地球物理学进展, 1994, 9 (1) : 90 –99.
Pei Jiangyun, He Qiaodeng. Inverse Q filtering according to Kjartansson model[J]. Progress in Geophysics, 1994, 9 (1) : 90 –99. |
| [15] | Kjartansson E. Constant Q wave propagation and attenuation[J]. Jouranl of Geophysical Research, 1979, 84 : 4737 –4748. DOI:10.1029/JB084iB09p04737 |
| [16] | Wang Y H. A stable and efficient approach of inverse Q filtering[J]. Geophysics, 2002, 67 (2) : 657 –663. DOI:10.1190/1.1468627 |
| [17] | Wang Y H. Inverse Q filtering for seismic resolution enhancement[J]. Geophysics, 2006, 71 (3) : 51 –61. DOI:10.1190/1.2192912 |
| [18] | Zhang C, Ulrych T J. Seismic absorption compensation:A least-squares inverse scheme[J]. Geophysics, 2007, 72 (6) : R109 –R114. DOI:10.1190/1.2766467 |
| [19] |
姚振兴, 高星, 李维新. 用于深度域地震剖面衰减与频散补偿的反Q滤波方法[J].
地球物理学报, 2003, 46 (2) : 229 –233.
Yao Zhenxing, Gao Xing, Li Weixin. The forward Q method for compensating attenuation and frequency dispersion used in the seismic profile of depth domain[J]. Chinese Journal of Geophysics, 2003, 46 (2) : 229 –233. |
| [20] | Durak L, Arikan O. Short-time Fourier transform:Two fundamental properties and optimal implementation[J]. IEEE Trans. on signal Processing, 2003, 51 (5) : 1231 –1242. DOI:10.1109/TSP.2003.810293 |
| [21] | Gabor D. Theory of Communication[J]. Journal of IEEE, 1946, 93 (3) : 429 –457. |
| [22] | Rioul O, Vetterli M. Wavelets and signal processing[J]. IEEE Signal Processing, 1991, 8 (4) : 14 –38. DOI:10.1109/79.91217 |
| [23] | Stockwell R G, Mansinha L, Lowe R P. Localization of the complex spectrum:The S transform[J]. IEEE Transactions on signal processing, 1996, 44 (4) : 998 –1001. DOI:10.1109/78.492555 |
| [24] | McFadden P D, Cook J G, Forster L M. Decomposition of gear vibration signals by generalized S-transform[J]. Mechnical Systems and Signal Process, 1999, 13 (4) : 691 –707. |
| [25] | Pinnegar C R, Mansinha L. The S-transform with windows of arbitrary and varying shape[J]. Geophysics, 2003, 68 (1) : 381 –385. DOI:10.1190/1.1543223 |
| [26] |
高静怀, 陈文超, 李幼铭, 等. 广义S变换与薄互层地震响应分析[J].
地球物理学报, 2003, 46 (4) : 526 –532.
Gao Jinghuai, Chen Wenchao, Li Youming, et al. Generalized S transform and seismic response analysis of thin interbeds[J]. Chinese Journal of Geophysics, 2003, 46 (4) : 526 –532. |
| [27] | Margrave G F. Theory of nonstationary linear filtering in the Fourier domain with application to time-variant filtering[J]. Geophysics, 1998, 63 : 244 –259. DOI:10.1190/1.1444318 |
 2015, Vol. 37
2015, Vol. 37


