钻柱与井壁的接触、钻头与岩石的相互作用会引起钻柱轴向、横向和周向形式的振动,在这些振动形式中,黏滑振动的危害最为严重[1]。钻柱黏滑振动是由钻头、钻柱与井底、井壁之间的接触非线性引起的,在这些非线性接触作用力的影响下,可以引起钻柱间歇性地高速运动和黏滞静止的周期性运动[2]。钻柱黏滑会在钻头和钻柱中引发周期性波动应力与应变,从而加快钻柱和钻头的疲劳失效,影响钻头的破岩效率,轻则降低钻速,增加钻井成本,重则导致钻柱断裂、钻头失效,并引发地面设备故障或井下事故。
早在20世纪80年代,国外的研究人员就发现了钻柱的黏滑现象并对其进行了较为深入的研究[3-4]。大多数学者将钻柱简化为具有扭转刚度和转动惯量的扭摆,建立了钻柱扭转振动模型。文献[5]结合Coulomb摩擦模型,分析了钻井阻尼、转盘转动惯量和转速对黏滑振动的影响,并将理论与现场实测结果进行了比较分析,指出了黏滑的危害。文献[6]采用连续指数形式的干摩擦模型,分析了扭转固有频率、转速与黏滞阻尼对钻柱黏滑运动的影响,并提出了临界转速、钻杆临界长度、临界黏滞阻尼的概念。文献[7]建立了钻柱黏滑与涡动动力学模型,利用突变理论解释了出现钻柱涡动后,黏滑振动消失这一现象。Richard T等人的研究表明,钻柱黏滑与轴向振动与钻头的破岩过程密切相关[8]。文献[9]考虑了钻头的破岩过程,以及钻头与井底摩擦接触界面之间的钻头--岩石相互作用,建立了一个耦合钻柱轴向振动与扭转振动的集中参数钻柱动力学模型;文献[10]利用这一模型研究了钻柱的黏滑振动现象,指出钻柱扭矩和角速度的变化是钻柱系统的动力学行为响应,而非钻头-岩石相互作用所固有的现象。文献[11]建立了一个通用的、考虑转盘、钻杆、钻铤和钻头组成的四自由度集中参数钻柱黏滑动力学模型。文献[12]对更高维钻柱黏滑动力学系统开展了研究。文献[13]比较分析了具有不同自由度和3种复杂程度各异的摩擦模型对钻柱动力学行为的影响。文献[14]根据钻柱轴向振动和扭转振动在时间尺度上的差异对动力学方程进行解耦处理,而文献[15]对解耦后的轴向振动方程采用平均法和奇异摄动法求得相应的半解析解,并且建立一个无轴向刚度和阻尼的钻柱动力学模型,来近似获得黏滑振动极限环参数。
一些研究人员采用有限元方法研究了钻柱黏滑振动,文献[1]用拉格朗日方法推导了钻柱运动的动力学方程,考虑了钻柱扭转——弯曲耦合及轴向——弯曲的几何非线性耦合,结合钻柱重力、陀螺效应和黏滑,详细分析了钻柱的黏滑运动。文献[16]采用有限元法研究钻柱的黏滑振动,并获得了许多钻柱自激振动的新特征。但集中质量模型能够对有限元模型中观察到复杂现象进行更加便捷、合理的定性描述,集中参数方法也允许对模型进行更加深入的分析,能够更为抽象地把握引起振动的机理。
在黏滑抑制和钻柱振动控制研究方面,文献[9]研究了钻头-岩石的相互作用机理,提出了速度弱化和速度强化两种形式,并提出在井口和BHA处分别进行黏滑振动的控制。文献[17]提出了通过调节钻压来消除黏滑,并建立了D-OSKIL来消除黏滑的技术。而文献[18]采用改变转盘转速的途径来消除黏滑,并在转盘输入端引入PI或PID控制器。但文献[19-20]均认为在复杂的钻井条件下,仅靠钻压和转盘转速的调节不可能有效地消除钻柱的自激振动与跳钻,并分别引入有反馈主动阻尼控制系统和线性二次型调节(LQR)控制器来消除钻柱的黏滑振动。文献[19]将钻柱看成是一个旋转扭摆,指出在钻柱顶部应用阻尼控制,或利用钻井液的黏滞性,可以有效地避免钻柱黏滑;文献[20]则建立了一个耦合了扭转和横向弯曲振动的钻柱动力学系统。文献[21]提出在钻柱轴向上施加一个主动控制,能够有效地消除黏滑和跳钻。文献[22-23]在研究四自由度集中参数模型的基础上,探讨了基于滑模控制器的控制方法,并分析了这一控制方法的有效性。文献[24]提出了钻柱黏滑振动的串联控制和分散控制两种方案。
国内学者也十分重视钻柱黏滑振动的研究。黄根炉等开展了大位移井钻柱黏滑振动机理分析及减振研究,给出了钻柱产生黏滑振动的判别式,分析了钻柱黏滑振动的影响因素及防止和消除钻柱黏滑振动可能的途径和措施,并对顶部扭矩负反馈减振方法进行了讨论,给出了其数值模拟结果[25]。韩春杰等分析了在钻头与地层扭矩及钻柱与井壁间摩阻扭矩作用下钻柱的动态行为,给出了钻柱所受摩阻力与钻柱动态位移之间的函数关系[26]。牟海维等分析了黏滑振动的运动方程,得到钻柱黏滑振动的一般规律[27]。祝效华等对PDC钻头的黏滑振动进行了系统的研究,认为外激频率与钻柱固有频率所引发的共振以及下部钻具的偏心钻进是引起黏滑振动的重要原因[28]。彭刚等分析了粘附卡钻发生条件和机理,介绍了加压解卡的原理[29]。楼一珊在钻井钻柱力学分析的基础上,建立了深井钻柱临界转速的计算模型[30]。
由此可见,钻柱黏滑是一个非常复杂的问题,如何将钻柱动力学应用于现场,实现钻柱振动的有效控制和利用是一个十分值得研究的课题。本文引入钻柱动力学仿真,针对现场的不同情况,开发了一个面向现场应用的钻柱动力学仿真器,并对钻柱的动力学行为开展了系统的研究,在此基础上获得了进行钻柱黏滑振动控制的有用信息。
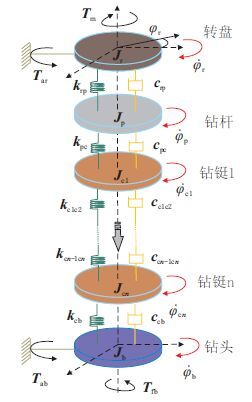
1 多维钻柱黏滑振动仿真系统本文在前人研究的基础上,考虑钻杆和钻铤力学特性的差异性,建立了钻柱多维扭转振动动力学方程。
1.1 钻柱多维扭转振动模型基于实际工况做如下假设:(1) 井眼为理想的直井;(2) 钻柱为转盘驱动;(3) 转盘、钻杆、钻柱和钻头被看作具有集中参数的质量块,并由具有扭转刚度的弹簧和阻尼连接。
如图 1所示,
 |
| 图1 钻柱多维扭转模型 Fig. 1 Drillstring multi-dimensional torsion model |
转盘在工作力矩
黏性摩擦力矩
钻头在钻柱的带动下以角速度
| ${{{T}}_{{\rm{fb}}}} = \left\{ {\begin{array}{*{20}{l}} {{{{T}}_{{\rm{eb}}}}}&{{{\dot \varphi }_{\rm{b}}} < {{\dot \varphi }_{{\rm{b0}}}}{{{T}}_{{\rm{eb}}}} < {{{T}}_{{\rm{sb}}}}}\\ {{{{T}}_{{\rm{sb}}}}{\mathop{\rm sgn}} {{{T}}_{{\rm{eb}}}}}&{{{\dot \varphi }_{\rm{b}}} < {{\dot \varphi }_{{\rm{b0}}}}{{{T}}_{{\rm{eb}}}} \geqslant {{{T}}_{{\rm{sb}}}}}\\ {{{{W}}_{{\rm{ob}}}}{R_{\rm{b}}}{\mu _{\rm{b}}}({{\dot \varphi }_{\rm{b}}}){\mathop{\rm sgn}} {{\dot \varphi }_{\rm{b}}}}&{{{\dot \varphi }_{\rm{b}}} \geqslant {{\dot \varphi }_{{\rm{b0}}}}} \end{array}} \right. $ | (1) |
式中:
干摩擦系数
| ${\mu _{\rm{b}}}({\dot \varphi _{\rm{b}}}) = {\mu _{{\rm{cb}}}} + ({\mu _{{\rm{sb}}}} - {\mu _{{\rm{cb}}}}){{\rm{e}}^{ - {\gamma _{\rm{b}}}{{\dot \varphi }_{\rm{b}}}}}$ | (2) |
式中:
转盘和钻头是通过钻杆和钻铤连接的,此模型将其简化为n个具有集中参数的质量块和n+1组具有扭转刚度的弹簧及阻尼。钻杆和钻铤与井壁的摩擦现象可由这些阻尼近似描述。
1.2 钻柱扭转振动动力学方程在上述模型的基础上,分别对转盘、钻柱、钻铤和钻头中的每一集中质量单元进行受力分析,由此建立以下钻柱系统动力学平衡方程
| $\left\{ \begin{array}{l} {{{J}}_{\rm{r}}}{{\ddot \varphi }_{\rm{r}}} + {{{c}}_{{\rm{rp}}}}({{\dot \varphi }_{\rm{r}}} - {{\dot \varphi }_{\rm{p}}}) + {{{k}}_{{\rm{rp}}}}({\varphi _{\rm{r}}} - {\varphi _{\rm{p}}}) = {{{T}}_{\rm{m}}} - {{{T}}_{{\rm{ar}}}}\\ {{{J}}_{\rm{p}}}{{\ddot \varphi }_{\rm{p}}} + {{{c}}_{{\rm{pc}}}}({{\dot \varphi }_{\rm{p}}} - {{\dot \varphi }_{{{\rm{c}}_{\rm{1}}}}}) + {{{k}}_{{\rm{pc}}}}({\varphi _{\rm{p}}} - {\varphi _{{{\rm{c}}_{\rm{1}}}}}) - {{{c}}_{{\rm{rp}}}}({{\dot \varphi }_{\rm{r}}} - {{\dot \varphi }_{\rm{p}}}) - {{{k}}_{{\rm{rp}}}}({\varphi _{\rm{r}}} - {\varphi _{\rm{p}}}) = 0\\ {{{J}}_{{{\rm{c}}_{\rm{1}}}}}{{\ddot \varphi }_{{{\rm{c}}_{\rm{1}}}}} + {{{c}}_{{{\rm{c}}_{\rm{1}}}{{\rm{c}}_{\rm{2}}}}}({{\dot \varphi }_{{{\rm{c}}_{\rm{1}}}}} -\\ {{\dot \varphi }_{{{\rm{c}}_{\rm{2}}}}}) + {{{k}}_{{{\rm{c}}_{\rm{1}}}{{\rm{c}}_{\rm{2}}}}}({\varphi _{{{\rm{c}}_{\rm{1}}}}} - {\varphi _{{{\rm{c}}_{\rm{2}}}}}) - {{{c}}_{{\rm{pc}}}}({{\dot \varphi }_{\rm{p}}} - {{\dot \varphi }_{{{\rm{c}}_{\rm{1}}}}}) - {{{k}}_{{\rm{pc}}}}({\phi _{\rm{p}}} - {\varphi _{{{\rm{c}}_{\rm{1}}}}}) = 0\\ {\rm{\cdot}}\\ {\rm{\cdot}}\\ {\rm{\cdot}}\\ {{{J}}_{{{\rm{c}}_n}}}{{\ddot \varphi }_{{{\rm{c}}_n}}} + {{{c}}_{{\rm{cb}}}}({{\dot \varphi }_{{{\rm{c}}_n}}} - {{\dot \varphi }_{\rm{b}}}) + \\ {{{k}}_{{\rm{cb}}}}({\varphi _{{{\rm{c}}_n}}} - {\varphi _{\rm{b}}}) - {{{c}}_{{{\rm{c}}_{n - {\rm{1}}}}{{\rm{c}}_n}}}({{\dot \varphi }_{{{\rm{c}}_{n - {\rm{1}}}}}} - {{\dot \varphi }_{{{\rm{c}}_n}}}) - {{{k}}_{{{\rm{c}}_{n - {\rm{1}}}}{{\rm{c}}_n}}}({\varphi _{{{\rm{c}}_{n - {\rm{1}}}}}} - {\varphi _{{{\rm{c}}_n}}}) = 0\\ {{{J}}_{\rm{b}}}{{\ddot \varphi }_{\rm{b}}} - {{{c}}_{{\rm{cb}}}}({{\dot \varphi }_{{{\rm{c}}_n}}} - {{\dot \varphi }_{\rm{b}}}) - {{{k}}_{{\rm{cb}}}}({\varphi _{{{\rm{c}}_n}}} - {\varphi _{\rm{b}}}) = - {{{T}}_{{\rm{ab}}}} - {{{T}}_{{\rm{fb}}}} \end{array} \right.$ | (3) |
式中:
将式(3)等式左右各项进行累加可以得到
| ${{{T}}_{\rm{m}}} - {{{T}}_{{\rm{ar}}}} - {{{T}}_{{\rm{ab}}}} - {{{T}}_{{\rm{fb}}}} = {{{J}}_{\rm{r}}}{\ddot \varphi _{\rm{r}}} + {{{J}}_{\rm{p}}}{\ddot \varphi _{\rm{p}}} + {{{J}}_{{{\rm{c}}_{\rm{1}}}}}{\ddot \varphi _{{{\rm{c}}_{\rm{1}}}}} + {\rm{\cdot\cdot\cdot\cdot\cdot\cdot}} + {{{J}}_{{{\rm{c}}_n}}}{\ddot \varphi _{{{\rm{c}}_n}}} + {{{J}}_{\rm{b}}}{\ddot \varphi _{\rm{b}}}$ | (4) |
| ${\ddot \varphi _{\rm{b}}} = \dfrac{{{{{T}}_{\rm{m}}} - {{{T}}_{{\rm{ar}}}} - {{{T}}_{{\rm{ab}}}} - {{{T}}_{{\rm{fb}}}}{\rm{ - }}\left( {{{{J}}_{\rm{r}}}{{\ddot \varphi }_{\rm{r}}} + {{{J}}_{\rm{p}}}{{\ddot \varphi }_{\rm{p}}} + {{{J}}_{{{\rm{c}}_{\rm{1}}}}}{{\ddot \varphi }_{{{\rm{c}}_{\rm{1}}}}} + {\rm{\cdot\cdot\cdot\cdot\cdot\cdot}} + {{{J}}_{{{\rm{c}}_n}}}{{\ddot \varphi }_{{{\rm{c}}_n}}}} \right)}}{{{{{J}}_{\rm{b}}}}}$ | (5) |
| $\int_{{t_0}}^{{t_1}} {{{\ddot \varphi }_{\rm{b}}}} {\rm{d}}t =\\ \int_{{t_0}}^{{t_1}} {\dfrac{{{{{T}}_{\rm{m}}} - {{{T}}_{{\rm{ar}}}} - {{{T}}_{{\rm{ab}}}} - {{{T}}_{{\rm{fb}}}}}}{{{{{J}}_{\rm{b}}}}}} {\rm{d}}t -\\ \int_{{t_0}}^{{t_1}} {\left( {{{{J}}_{\rm{r}}}{{\ddot \varphi }_{\rm{r}}} + {{{J}}_{\rm{p}}}{{\ddot \varphi }_{\rm{p}}} + {{{J}}_{{{\rm{c}}_{\rm{1}}}}}{{\ddot \varphi }_{{{\rm{c}}_{\rm{1}}}}} + {\rm{\cdot\cdot\cdot\cdot\cdot\cdot}} + {{{J}}_{{{\rm{c}}_n}}}{{\ddot \phi }_{{{\rm{c}}_n}}}} \right)} {\rm{d}}t$ | (6) |
由此可以获得钻头角速度的计算公式为
| ${\omega _{\rm{b}}} = {\omega _{{\rm{b0}}}}{\rm{ - }}\dfrac{1}{{{{{J}}_{\rm{b}}}}}\sum\limits_{k = {\rm{r\backslash p\backslash }}{{\rm{c}}_{\rm{1}}}{\rm{\backslash }}{{\rm{c}}_{\rm{2}}}{\rm{\backslash }}......{\rm{\backslash }}{{\rm{c}}_n}} {{{{J}}_k}\left( {{\omega _k} - {\omega _{k0}}} \right)} +\\ \dfrac{1}{{{{{J}}_{\rm{b}}}}}\int_0^{{t_{\rm{z}}}} {\left( {{{{T}}_{\rm{m}}} - {{{T}}_{{\rm{ar}}}} - {{{T}}_{{\rm{ab}}}}} \right){\rm{d}}t} {\rm{ - }}\dfrac{1}{{{{{J}}_{\rm{b}}}}}\int_0^{{t_{\rm{z}}}} {{{{T}}_{{\rm{fb}}}}{\rm{d}}t}$ | (7) |
式中:
当钻头角速度
| ${\omega _{\rm{b}}} = {\omega _{{\rm{b0}}}}{\rm{ - }}\dfrac{1}{{{{{J}}_{\rm{b}}}}} \sum\limits_{k = {\rm{r\backslash p\backslash c}}_{\rm{1}} {\rm{\backslash c}}_{\rm{2}} {\rm{\backslash }}......{\rm{\backslash c}}_n } {{{J}}_k \left( {\omega _k - \omega _{k{\rm{0}}} } \right)}+ \\ \dfrac{1}{{{{{J}}_{\rm{b}}}}}\int_0^{{t_{\rm{z}}}} {\left( {{{{T}}_{\rm{m}}} - {{{T}}_{{\rm{ar}}}} - {{{T}}_{{\rm{ab}}}} - {{{T}}_{{\rm{sb}}}}} \right){\rm{d}}t} < {\dot \phi _{{\rm{b0}}}}$ | (8) |
| ${\overline{{{T}}}_{\rm{m}}} < \dfrac{1}{{{t_{\rm{z}}}}}\int_0^{{t_{\rm{z}}}} {\left( {{{{T}}_{{\rm{ar}}}} + {{{T}}_{{\rm{ab}}}} + {{{T}}_{{\rm{sb}}}}} \right){\rm{d}}t} + \dfrac{1}{{{t_{\rm{z}}}}}\left[{{{{J}}_{\rm{b}}}\left( {{{\dot \varphi }_{{\rm{b0}}}} - {\omega _{{\rm{b0}}}}} \right) +\\ \sum\limits_{k = {\rm{r\backslash p\backslash }}{{\rm{c}}_{\rm{1}}}{\rm{\backslash }}{{\rm{c}}_{\rm{2}}}{\rm{\backslash }}......{\rm{\backslash }}{{\rm{c}}_n}} {{{{J}}_k}\left( {{\omega _k} - {\omega _{k0}}} \right)} } \right]$ | (9) |
式中:
当钻头角速度
| ${\omega _{\rm{b}}} = {\omega _{{\rm{b0}}}} + \dfrac{1}{{{{{J}}_{\rm{b}}}}}\\ \left[{\int_0^{{t_{\rm{z}}}} {\left( {{{{T}}_{\rm{m}}} - {{{T}}_{{\rm{ar}}}} - {{{T}}_{{\rm{ab}}}} - {{{W}}_{{\rm{ob}}}}{R_{\rm{b}}}{\mu _{{\rm{cb}}}}} \right){\rm{d}}t} - \sum\limits_{k = {\rm{r\backslash p\backslash }}{{\rm{c}}_{\rm{1}}}{\rm{\backslash }}{{\rm{c}}_{\rm{2}}}{\rm{\backslash }}......{\rm{\backslash }}{{\rm{c}}_n}} {\left( {{\omega _k} - {\omega _{k0}}} \right)} } \right]\\ \geqslant {\dot \varphi _{{\rm{b0}}}}$ | (10) |
| ${\overline{{{T}}}_{\rm{m}}} \geqslant \dfrac{1}{{{t_{\rm{z}}}}}\int_0^{{t_{\rm{z}}}} {\left( {{{{T}}_{{\rm{ar}}}} + {{{T}}_{{\rm{ab}}}} + {{{W}}_{{\rm{ob}}}}{R_{\rm{b}}}{\mu _{{\rm{cb}}}}} \right){\rm{d}}t} +\\ \dfrac{1}{{{t_{\rm{z}}}}}\left[{{{{J}}_{\rm{b}}}\left( {{{\dot \varphi }_{{\rm{b0}}}} - {\omega _{{\rm{b0}}}}} \right) + \sum\limits_{k = {\rm{r\backslash p\backslash }}{{\rm{c}}_{\rm{1}}}{\rm{\backslash }}{{\rm{c}}_{\rm{2}}}{\rm{\backslash }}......{\rm{\backslash }}{{\rm{c}}_n}} {{{{J}}_k}\left( {{\omega _k} - {\omega _{k0}}} \right)} } \right]$ | (11) |
由于
(1) 当
尤其是当
(2) 当钻柱处于稳定转动状态时,各部分的角速度均等于转盘转速
(3) 当
从上面的分析中可以得到以下几点结论:(1) 为了避免钻柱的黏滑振动,控制的关键是转盘输入扭矩;(2) 提高转盘转速虽然可以在一定程度上控制钻柱的黏滑振动,但如果仅仅提高转速,不相应地提升输入扭矩
以方程组(3)为基础,可以开展钻柱多维扭转振动的动力学仿真研究。首先,利用实际工况下的钻柱和油井的基本数据,然后,利用图 2所示的仿真流程,开展了钻柱黏滑的系统仿真研究。
 |
| 图2 钻柱黏滑振动动力学仿真流程图 Fig. 2 The flowchart of drillstring stick-slip vibration dynamics simulation |
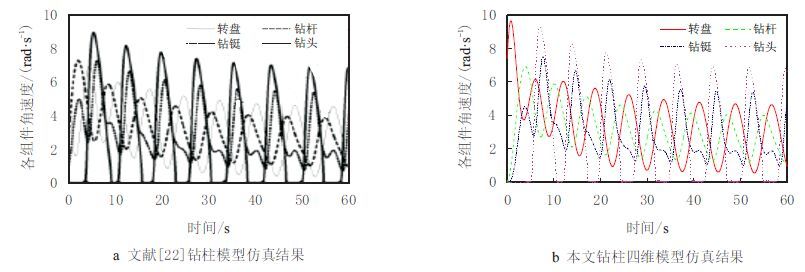
当把钻铤简化成一个集中质量块时,此钻柱模型即为四维钻柱模型。文献[22]已对四维扭转钻柱模型的黏滑振动进行了仿真分析。该钻柱模型的基本力学参数如下:
对比图 3a和图 3b可以看出,本文四维模型完全可以复现文献[22]的仿真结果。因此,在此基础上开展的多维钻柱黏滑振动仿真研究是可靠而有效的。
3 钻柱多维黏滑振动的系统仿真分析针对钻柱实际工况,下面分别对转盘转速、钻压、钻铤尺寸、钻铤刚度等重要参数对钻柱黏滑振动的影响进行仿真分析。
3.1 单因素对钻柱黏滑行为的影响分析以表 1参数作为基准值,开展了单因素对钻柱动力学系统黏滑行为的仿真研究。以转盘转速为例,钻柱系统的黏滑振动随着单因素的变化,理论上存在着以下几种不同的状态。
| 表1 钻柱黏滑振动系统仿真结果 Table 1 Systematic simulation results of drillstring stick-slip vibration |
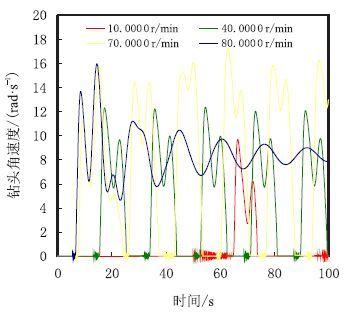
(1) 钻柱黏滑振动状态。在此状态下,钻头与钻柱发生黏滑振动; 并且转盘转速越低,钻柱黏滑周期越大,钻头黏滞时间也越长,钻头的转速波动幅度也越大。图 4为恒转盘输入功率条件下,不同转盘转速下钻头黏滑振动的动态仿真结果。从图上可以看出,当转盘转速只有1.05 rad/s(10 r/min)时,钻头的最大波动转速可以达到9.67 rad/s,是转盘转速的9倍多。当转盘转速为40.000~0 r/min 和70.000~0 r/min时,钻头最大转速均在转盘转速的2倍以上。
 |
| 图4 不同转盘转速下钻头黏滑仿真结果 Fig. 4 Simulation results of bit stick-slip at different rotary speeds |
(2) 无黏滑转速波动状态,这是一个理论上存在的状态,是一个不稳定的临界值。例如,当转盘转速超过某一临界转速时,钻柱与钻头的黏滞状态段转变成为钻头的低速旋转,黏滞静止段收缩成为一个点,并且存在转速的波动,可以称此临界转速为第一黏滑临界转速。这一波动量随着转盘转速的增大而迅速减小,并趋近于另外一个稳定的临界转速,可以称此临界转速为第二黏滑临界转速。在第一和第二临界转速之间,钻柱系统进入混沌状态,黏滑和稳定状态交替出现、不可预测。鉴于钻柱黏滑运动的混沌特征,要获得这两个临界转速的数值是很难的。
(3) 当转盘转速超过钻柱第二黏滑临界值时,在启动后经历几次扭转振动,整个钻柱就与转盘同步进入稳定的转动状态。如图 5所示,当转盘转速为70.200~0 r/min时,钻柱处于黏滑转动状态;当转盘转速为70.220~0 r/min时,钻柱经历几次扭转振动后进入稳定的转动状态,随着时间的增长,钻头几乎与转盘同步转动且角速度波动微小。经过多次仿真确定此次仿真的临界转速约为70.217~3 r/min。
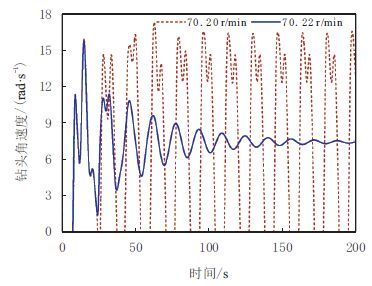 |
| 图5 转盘临界转速附近钻头转速仿真结果 Fig. 5 Simulation results of bit angular velocity near the critical rotary speed |
(4) 钻头的黏卡状态。当钻头的静止黏滞时间超过10 s时为钻头黏卡状态。钻柱在实际的黏滑振动过程中存在理论上的钻头黏卡状态。如图 6所示,当转盘转速为10.000~0 r/min时,钻头在积聚大量势能后才能克服钻头-岩石最大静摩擦力矩,并随之转动。此时由于大量势能在瞬间释放,导致钻头角速度瞬间达到转盘转速9倍以上,这种情况对钻头、钻铤的危害非常大。当转盘转速降低时,如图 6虚线所示,钻头会处于卡钻状态,此种状态下如果不调整其他参数而继续运转,钻柱会有被扭断的危险。
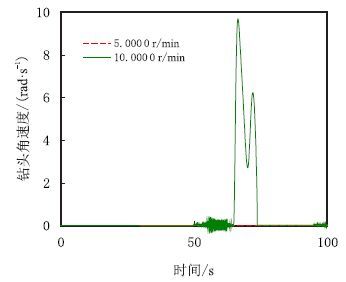 |
| 图6 低转盘转速下的卡钻现象 Fig. 6 Sticking phenomenon with low rotary speed |
仿真研究表明,在影响黏滑系统振动的各种因素中,都普遍存在着上述4种黏滑振动状态。例如,图 7就是在不同的钻压下,钻柱黏滑扭转振动的仿真结果。当转盘功率不变的条件下,当钻压小于80.000 kN时,钻柱系统除了启动阶段存在一定的黏滑效应,在稳定阶段不存在黏滑振动;当钻压超过一定值后,钻头摩擦力相应增大,在稳定阶段便会发生无黏滑转速波动状态;这是一个很不稳定的状态,钻压稍微波动就会在稳定和黏滑之间转变,因此,继续增大钻压会导致钻柱进入黏滑振动状态,若钻压继续增加就会导致卡钻。表 1是钻柱系统各因素在以仿真实例的模型参数为基准值的条件下,时间步长dt取0.010 s获得的钻柱单因素变化的黏滑仿真结果汇总。
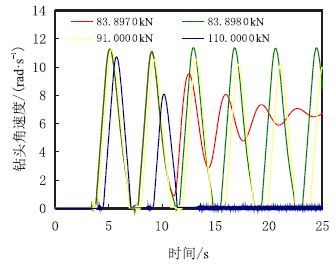 |
| 图7 不同钻压下钻头黏滑仿真结果 Fig. 7 Simulation results of bit stick-slip with different WOB |
通过上述仿真,可以得出如下结论:(1) 为了克服钻头黏滑现象,应当增大转盘、钻铤转动惯量,减少钻杆与钻头的转动惯量,或者降低钻铤的刚度;(2) 为了克服钻头黏滑现象,应当降低转盘、钻杆的黏性系数,增大钻铤与钻头的黏性系数;(3) 调整钻压与转速,可以直接改变钻柱的旋转状态,低钻压、高转速可以有效地避免钻柱的黏滑振动。
3.2 钻柱参数对钻柱黏滑行为的影响分析以上研究是在钻柱黏滑振动系统某一因素变化,其他因素保持为仿真实例参数值不变的条件下获得的动态仿真结果。实际上管柱的刚度与转动惯量两者有着密切的联系,管柱长度、直径的改变直接影响着管柱转动惯流量和刚度数值。因此,本文针对管柱长度和内外径参数的变化开展了相应的仿真研究。
3.2.1 管柱长度变化对管柱振动系统的影响(1) 钻杆长度变化对振动系统影响规律的研究 随着管柱长度的增大,管柱的刚度变小,转动惯量变大。管柱刚度降低、转动惯量的增大易在管柱内部积聚势能,影响机械能量的传递速率,不利于抵抗钻头的黏滑运动。仿真表明,如果取仿真步长dt=0.010 s,对于式(3)及仿真实例的钻柱黏滑系统,有:
当钻杆长度
因此,钻柱系统极易在中深部地层钻进时产生黏滑运动。而且,随着钻杆长度的增大,黏滑振动周期也相应增大。利用仿真数据可以得到钻杆长度和钻柱黏滑周期之间的回归结果如图 8所示,回归方程如下
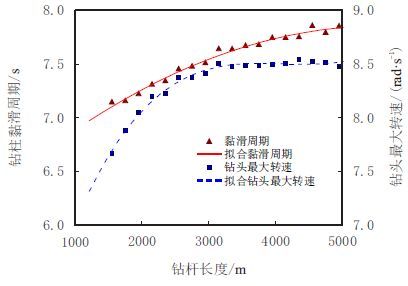 |
| 图8 钻杆长度对钻头黏滑振动的影响 Fig. 8 Impacts of drillpipe length on bit stick-slip vibration |
| $T=6.418+5.130\times{10^{{\rm{-}}4}}{L_{\rm{p}}}{\rm{ - }}4.569\times$ ${10^{-8}}{L_{\rm{p}}}^2\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&{} \end{array}}&{}&{} \end{array}\begin{array}{*{20}{c}} {}{}{ {R = 0.98511} } \end{array}$ | (12) |
| ${\omega _{{\rm{b}}\max }} = 5.039 + 0.002{L_{\rm{p}}} - 6.295 \times {10^{ - 7}}{L_{\rm{p}}}^2 + $ $5.109 \times{10^{ - 11}}{L_{\rm{p}}}^3\begin{array}{*{20}{c}} {}&{} \end{array}\begin{array}{*{20}{c}} {}&{ {R = 0.98795} } \end{array}$ | (13) |
式中:T—— 黏滑振动周期,s;
R—— 相关性系数。
(2) 钻铤长度变化对振动系统影响规律的研究
仿真表明,与钻杆仿真得到的钻柱动力学行为相反,当钻铤段较短时,系统处于黏滑状态,而当钻铤长度超过一定的数值,钻柱系统将进入稳定转动状态。另外,随着钻铤长度的增大,黏滑运动的振动周期也相应增大。当dt=0.010 s时,对于式(3)及仿真实例的钻柱黏滑系统,有
当钻铤长度
因此,为了削弱黏滑现象,应当适当增大钻铤的长度。
类似地,可以获得钻铤长度和钻柱黏滑周期之间的回归结果如图 9所示,回归方程如下
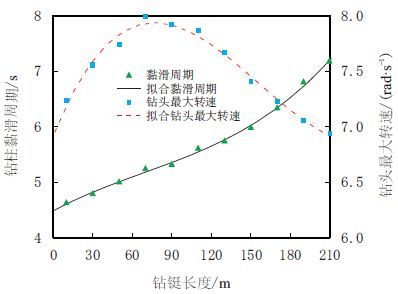 |
| 图9 钻铤长度对钻头黏滑振动的影响 Fig. 9 Impacts of drillcollar length on bit stick-slip vibration |
| $T = 4.482 + 0.013{L_{\rm{c}}} + 2.958 \times {10^{ - 7}}{L_{\rm{c}}}^3\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&{} \end{array}}&{}&{} \end{array}\begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {}&{} \end{array}}&{ {R = 0.9972} } \end{array}$ | (14) |
| ${\omega _{{\rm{b}}\max }} = 6.913 + 0.03{L_{\rm{c}}} - 2.575 \times {10^{ - 4}}{L_{\rm{c}}}^2 + \\ 5.494 \times {10^{ - 7}}{L_{\rm{c}}}^3\begin{array}{*{20}{c}} {}&{} \end{array}\begin{array}{*{20}{c}} {}&{{R = 0.98246} } \end{array}$ | (15) |
管柱内径减小或外径增大,可使管柱的转动惯量和刚度都增大。在式(3)的钻柱黏滑振动系统中,如果保持其他参数不变,只改变管柱外径,管柱的黏滑振动也体现出明显的混沌运动,在稳态和黏滑运动之间的转变没有规律可循。因此,改变管柱外径不可能控制管柱的黏滑运动。
3.3 时间步长对钻柱黏滑仿真的影响
对于一个系统状态极易受到前一状态影响的混沌动力学系统而言,仿真过程中的数值误差可以对系统的行为产生明显的影响。例如,当dt取0.010 s时,钻杆长度
(1) 对钻柱动力学方程所做的理论分析表明,避免钻柱黏滑振动的关键是控制转盘平均输入扭矩。提高转盘转速或调节钻压虽然可以在一定程度上控制钻柱的黏滑振动,但如果仅仅依靠对这两个参数的调整是不可能彻底消除钻柱黏滑振动的。
(2) 仿真研究表明,钻柱的旋转运动存在着稳定旋转、无黏滑转速波动状态、黏滑振动和钻头黏卡这4种不同的状态。并且依据系统的不同行为状态,钻柱动力学参数通常会存在第一和第二黏滑临界点。当某动力学系统参数处于这两个临界点之间时,钻柱进入不稳定的混沌运动状态。
(3) 通过研究单因素对钻柱黏滑振动系统的动力学行为的影响,可以得出相应的控制黏滑的方法。增大转盘、钻铤转动惯量,减少钻杆与钻头的转动惯量,降低钻铤的刚度,可以抑制或消除钻头黏滑现象。调整钻压与转速,可以直接改变钻柱的旋转状态,适当的低钻压、高转速可以有效地避免钻柱的黏滑振动。
(4) 结合实际管柱动力学参数的仿真结果表明,钻杆越长,就越容易引起钻柱的黏滑振动。为了避免钻柱黏滑,应当尽可能增大钻铤长度。另外,利用改变管柱内、外径来控制管柱的黏滑运动是不可能的。
| [1] | Khulief Y A, Al-Sulaiman F A, Bashmal S. Vibration analysis of drillstrings with self-excited stick-slip oscillations[J]. Journal of Sound and Vibration, 2007, 299 (3) : 540 –558. DOI:10.1016/j.jsv.2006.06.065 |
| [2] | 吕苗荣. 石油工程管柱力学[M]. 北京: 中国石化出版社, 2012 . |
| [3] | Eronini I E, Somerton W H, Auslander D M. A dynamic model for rotary rock drilling[J]. Journal of Energy Resources Technology, 1982, 104 (2) : 108 –120. DOI:10.1115/1.3230387 |
| [4] | Belokoby'skii S V, Prokopove V K. Friction-induced selfexcited vibrations of drill rig with exponential drag law[J]. Sov.Appl.Mech, 1983 : 89 –101. |
| [5] | Kyllingstad A, Halsey G W. A study of slip/stick motion of the bit[C]. SPE 16659, 1988. |
| [6] | Lin Y Q, Wang Y H. Stick-slip vibration of the drill strings[J]. Journal of Manufacturing Science and Engineering, 1991, 113 (1) : 38 –43. DOI:10.1115/1.2899620 |
| [7] | Leine R I, Van Campen D H, Keultjes W J. Stick-slip whirl interaction in drillstring dynamics[J]. Journal of Vibration and Acoustics, 2002, 124 (2) : 209 –220. DOI:10.1115/1.1452745 |
| [8] | Richard T, Detournay E. Stick-slip motion in a friction oscillator with normal and tangential mode coupling[J]. Comptes Rendus de l'Académie des Sciences-Series ⅡB:Mechanics, 2000, 328 (9) : 671 –678. DOI:10.1016/S1620-7742(00)01240-X |
| [9] | Richard T, Germay C, Detournay E. Self-excited stickslip oscillations of drill bits[J]. Comptes Rendus Mé-canique, 2004, 332 (8) : 619 –626. DOI:10.1016/j.crme.2004.01.016 |
| [10] | Richard T, Germay C, Detournay E. A simplified model to explore the root cause of stick-slip vibrations in drilling systems with drag bits[J]. Journal of Sound and Vibration, 2007, 305 (3) : 432 –456. DOI:10.1016/j.jsv.2007.04.015 |
| [11] | Zamanian M, Khadem S E, Ghazavi M R. Stick-slip oscillations of drag bits by considering damping of drilling mud and active damping system[J]. Journal of Petroleum Science and Engineering, 2007, 59 (3-4) : 289 –299. DOI:10.1016/j.petrol.2007.04.008 |
| [12] | Navarro-López E M, Cortés D. Avoiding harmful oscillations in a drillstring through dynamical analysis[J]. Journal of Sound and Vibration, 2007, 307 (1) : 152 –171. |
| [13] | Silveira M, Wiercigroch M. Low dimensional models for stick-slip vibration of drill-strings[J]. Journal of Physics:Conference Series, 2009, 181 (1) : 12 –56. |
| [14] | Germay C, Van de Wouw N, Nijmeijer H, et al. Nonlinear drillstring dynamics analysis[J]. SIAM Journal on Applied Dynamical Systems, 2009, 8 (2) : 527 –553. DOI:10.1137/060675848 |
| [15] | Besselink B, van de Wouw N, Nijmeijer H. A semianalytical study of stick-slip oscillations in drilling systems[J]. Journal of Computational and Nonlinear Dynamics, 2011, 6 (2) : 21006 –21014. DOI:10.1115/1.4002386 |
| [16] | Christophe G, Vincent D, Emmanuel D. Multiple mode analysis of the self-excited vibrations of rotary drilling systems[J]. Journal of Sound and Vibration, 2009, 325 (1-2) : 362 –381. DOI:10.1016/j.jsv.2009.03.017 |
| [17] | Canudas-de-Wit C, Rubio F R, Corchero M A. A new mechanism for controlling stick-slip oscillations in oil well drillstrings[J]. IEEE Transactions on Control Systems Technology, 2008, 16 (6) : 1177 –1191. DOI:10.1109/TCST.2008.917873 |
| [18] | Tucker R W, Wang C. On the effective control of torsional vibrations of drillstring systems[J]. Journal of Sound and Vibration, 1999, 224 (1) : 101 –122. DOI:10.1006/jsvi.1999.2172 |
| [19] | Jansen J D, van den Steen L. Active damping of selfexcited torsional vibration in oil well drillstrings[J]. Journal of Sound and Vibration 1, 1995, 179 (4) : 647 –668. DOI:10.1006/jsvi.1995.0042 |
| [20] | Yigit A S, Christoforou A P. Coupled torsional and bending vibrations of actively controlled drillstrings[J]. Journal of Sound and Vibration, 2000, 234 (1) : 67 –83. DOI:10.1006/jsvi.1999.2854 |
| [21] | Yigit A S, Christoforou A P. Stick-slip and bit-bounce interaction in oil-well drillstrings[J]. Journal of Energy Resources Technology, 2006, 128 (4) : 268 –274. DOI:10.1115/1.2358141 |
| [22] | Navarro-López E M, Cortés D. Sliding-mode control of a multi-DOF oilwell drillstring with stick-slip oscillations[C]//American Control Conference, 2007, ACC'07, IEEE, 2007:3837-3842. |
| [23] | Navarro-López E M, Licéaga-Castro E. Non-desired transitions and sliding-mode control of a multi-DOF mechanical system with stick-slip oscillations[J]. Chaos, Solitons & Fractals, 2009, 41 (4) : 2035 –2044. |
| [24] | Puebla H, Alvarez-Ramirez J. Suppression of stick-slip in drillstrings:A control approach based on modeling error compensation[J]. Journal of Sound and Vibration, 2008, 310 (4) : 881 –901. |
| [25] |
黄根炉, 韩志勇. 大位移井钻柱粘滑振动机理分析及减振研究[J].
石油钻探技术, 2001, 29 (2) : 4 –6.
Huang Genlu, Han Zhiyong. Mechanism analysis on torsional stick-slip vibration of drillstring in extended reach well and some ways to its suppression[J]. Petroleum Drilling Techniques, 2001, 29 (2) : 4 –6. |
| [26] |
韩春杰, 阎铁. 大位移井钻柱"粘滞-滑动"规律研究[J].
天然气工业, 2004, 24 (11) : 58 –60.
Han Chunjie, Yan Tie. Research on the "strickingslipping" law of drillstring in extended-reach well[J]. Natural Gas Industry, 2004, 24 (11) : 58 –60. |
| [27] | 牟海维, 王瑛, 韩春杰. 钻柱的粘滑振动规律分析[J]. 石油机械, 2011, 39 (3) : 67 –69. |
| [28] |
祝效华, 汤历平, 孟苹苹, 等. PDC钻头黏滑振动机理分析[J].
石油矿场机械, 2012, 41 (4) : 13 –16.
Zhu Xiaohua, Tang Liping, Meng Pingping, et al. Stickslip vibration mechanism analysis of pdc bit[J]. Oil Field Equipment, 2012, 41 (4) : 13 –16. |
| [29] |
彭刚, 杨世军, 先齐. 加压解卡工艺在XS1井的应用[J].
天然气工业, 2012, 32 (10) : 71 –73.
Peng Gang, Yang Shijun, Xian Qi. Application of pressurization and getting unstuck technology in the XS1 well, Sichuan Basin[J]. Natural Gas Industry, 2012, 32 (10) : 71 –73. |
| [30] |
楼一珊. 深井钻柱临界转速的计算方法[J].
钻采工艺, 1999, 22 (4) : 3 –5.
Lou Yishan. How to calculate critical rpm of deep well drill string[J]. Drilling & Production Technology, 1999, 22 (4) : 3 –5. |
 2014, Vol. 36
2014, Vol. 36