2. 中国石化胜利油田分公司地质科学研究院, 山东 东营 257015;
3. 中国石化胜利油田分公司海洋采油厂, 山东 东营 257237
2. Geoscience Research Institute of Shengli Oilfield Branch Company, Dongying, Shandong 257015, China;
3. Haiyang Oil Production Plant of Shengli Oilfield Branch Company, Dongying, Shandong 257237, China
交联聚合物驱是在聚合物驱基础上发展起来的一项提高原油采收率新技术[1-9]。油藏数值模拟是交联聚合物驱研究的一个重要手段[10-14],模拟结果可为交联聚合物驱的驱油机理分析、注采条件优化、矿场实施效果预测和评价提供决策依据。在数值模拟过程中,超过80%的计算时间都用于求解渗流微分方程差分离散后得到的大型稀疏线性代数方程组,其性能好坏决定了油藏模拟的速度和质量[15-16]。其中,渗流微分方程差分格式的选择直接影响求解的稳定性和计算效率。为此,本文提出交联聚合物驱渗流微分方程采用Douglas差分格式,利用分步降维的思路并结合追赶法进行求解,能够大幅度提高模型的运算速度,同时保证了运算精度及稳定性。
1 交联聚合物驱数学模型交联聚合物驱是一个复杂的化学驱油过程,为了便于研究并尽可能多地考虑交联聚合物驱油机理,作如下假设:(1) 油藏中存在油、水两相渗流,油相中仅包含油组分,其他组分在水相中;(2) 流体渗流符合达西定律,且油、水相之间无质量交换;(3) 油藏岩石及流体微可压缩;(4) 考虑油、水相之间毛管压力和重力的影响;(5) 聚合物、交联剂等物质的加入不影响水相体积和密度的变化,不影响油相渗流和油相性质的变化;(6) 组分物质的扩散遵循Fick扩散定律,吸附遵循Langmuir等温吸附理论;(7) 化学反应只考虑聚合物和交联剂之间的交联反应;(8) 整个过程为等温渗流,因化学反应引起的温度变化忽略不计。在此基础上,推导得到交联聚合物驱的数学模型。
油组分的基本渗流微分方程
| $\nabla\!\cdot\!\left[\!{{F_{{\rm{Dc}}}}\!\cdot \dfrac{{{K_{\rm{o}}}}}{{{B_{\rm{o}}}{\mu _{\rm{o}}}}}\nabla\!\left(\! {{p_{\rm{o}}}\!-\!{F_{\rm{g}}} \cdot {\rho _{\rm{o}}}{\rm{g}}D} \right)} \right]\!+\! {q_{{\rm{ov}}}}\!=\!\dfrac{ \partial }{{ \partial t}}\left(\! {\dfrac{{\phi\!{S_{\rm{o}}}}}{{{B_{\rm{o}}}}}}\!\right) $ | (1) |
水组分的基本渗流微分方程
| $\nabla\!\cdot \left[\!{{F_{{\rm{Dc}}}}\!\cdot\! \dfrac{{{K_{\rm{w}}}}}{{{R_{{\rm{Kw}}}}{B_{\rm{w}}}{\mu _{\rm{w}}}}}\nabla \left(\!{{p_{\rm{w}}}\!-\!{F_{\rm{g}}}\!\cdot {\rho\!_{\rm{w}}}{\rm{g}}D} \right)} \right]\!+\!{q_{{\rm{wv}}}}\!=\hspace{2em}\!\dfrac{ \partial }{{ \partial t}}\left(\! {\dfrac{{\phi\!{S_{\rm{w}}}}}{{{B_{\rm{w}}}}}}\!\right)$ | (2) |
聚合物、交联聚合物和交联剂的基本渗流微分方程
| $\begin{align} & \nabla \cdot \left[ {{F}_{\text{Dc}}}\cdot \frac{{{K}_{\text{w}}}}{{{R}_{\text{Kw}}}{{\mu }_{\text{w}}}}\nabla \left( {{p}_{\text{w}}}-{{F}_{\text{g}}}\cdot {{\rho }_{\text{w}}}\text{g}D \right){{C}_{l\text{w}}}+\phi {{S}_{\text{w}}}{{\beta }_{l}}\nabla {{C}_{l\text{w}}} \right] \\ & +{{B}_{\text{w}}}{{q}_{\text{wv}}}{{C}_{l\text{w}}}+\phi {{S}_{\text{w}}}{{R}_{l}}=\frac{\partial }{\partial t}\left( \phi {{E}_{l}}{{S}_{\text{w}}}{{C}_{l\text{w}}}+\phi {{C}_{l\text{ad}}} \right) \\ \end{align}$ | (3) |
毛管压力方程
| ${p_{{\rm{cow}}}} = {p_{\rm{o}}} - {p_{\rm{w}}} = {p_{\rm{c}}}\left( {{S_{\rm{w}}},{\sigma _{{\rm{wo}}}}} \right)$ | (4) |
饱和度归一化方程
| ${S_{\rm{o}}} + {S_{\rm{w}}} = 1$ | (5) |
为了简单、准确地表征交联聚合物驱过程中的各种物理化学现象,对以下主要物化参数进行描述。
2.1 交联聚合物溶液黏度计算交联聚合物溶液黏度随浓度变化的方法较多,大多是一些经验关系式。考虑到一种交联聚合物体系对应一组特定的黏浓关系曲线。本文采用液相黏度的非线性混合函数插值关系式来确定水相黏度。
| $\ln{\mu_{\rm{w}}}=f({x_{\rm{P}}})\ln{\mu_{\rm{P}}}+ f({x_{\rm{G}}})\ln {\mu _{\rm{G}}}+\hspace{2em}\dfrac{{1-f({x_{\rm{P}}})- f({x_{\rm{G}}})}}{{1-{x_{\rm{P}}}-{x_{\rm{G}}}}}{x_{\rm{w}}}\ln\mu _{\rm{w}}^{'}$ | (6) |
利用Langmuir吸附等温式计算组分l的吸附浓度大小${C_{l{\rm{ad}}}}$
| ${C_{l{\rm{ad}}}} = \dfrac{{a{C_{l{\rm{w}}}}}}{{1 + b{C_{l{\rm{w}}}}}}$ | (7) |
由于聚合物、交联聚合物组分的吸附滞留,使得岩石孔隙介质的局部渗透率降低,定义水相渗透率降低系数来描述这一物理化学现象,计算关系式为
| ${R_{l{\rm{Kw}}}} = 1 + \dfrac{{\left( {{F_{l{\rm{rr}}}} - 1} \right){C_{l{\rm{ad}}}}}}{{{C_{l{\rm{ad}}\max }}}}$ | (8) |
| ${K_{\rm{w}}} = {K_{\rm{w}}^0}/\prod\limits_{l = {\rm{P}},{\rm{G}}} {{R_{l{\rm{Kw}}}}} $ | (9) |
聚合物和交联聚合物组分是高分子化合物,流经岩石多孔介质时不能遍及全部孔隙体积,将组分物质能到达的孔隙体积定义为可及孔隙体积。假定组分物质可及孔隙体积大小不变,岩石孔隙度为
| $E_l = \dfrac{{\phi _l }}{\phi },l = {\rm{G}},{\rm{P}}$ | (10) |
聚合物、交联聚合物或交联剂组分的扩散是通过定义该组分在水相中的扩散系数来体现的,其扩散通量与扩散系数间的关系可通过Fick扩散定律进行描述
| ${F_{lJ}} = - {D_{lJ}}\dfrac{{ \partial {C_{l{\rm{w}}}}}}{{ \partial J}}\quad \left\{ {\begin{array}{*{20}{l}} {l = {\rm{P}},{\rm{G}},{\rm{Cr}}}\\ {J = x,y,z} \end{array}} \right.$ | (11) |
目前,聚合物交联反应体系主要包括过渡金属交联体系、醛类交联体系和复合交联体系3大类[17]。其中,过渡金属交联体系中的聚合物/氯化铬模型最常见,该模型的反应方程式简记为
| ${\rm{polymer}} + n{\rm{Cr}}^{{\rm{3}} + } + m{\rm{H}}_2 {\rm{O}} \to {\rm{clpolymer}} + 3n{\rm{H}}^ +$ | (12) |
交联反应动力学模型为
| $\dfrac{{{\rm{d}}{C_{{\rm{Cr}}}}}}{{{\rm{d}}t}} = - n \cdot \alpha \cdot {C_{{\rm{Cr}}}}^{\rm{2}} \cdot {C_{\rm{P}}}^{\rm{2}}$ | (13) |
| $ - \dfrac{{{\rm{d}}{C_{\rm{P}}}}}{{{\rm{d}}t}} = \dfrac{{{\rm{d}}{C_{\rm{G}}}}}{{{\rm{d}}t}} = \alpha \cdot {C_{{\rm{Cr}}}}^{\rm{2}} \cdot {C_{\rm{P}}}^{\rm{2}}$ | (14) |
模型求解采用隐式求解压力、显式求解饱和度与组分浓度的方法。
对于二维或三维渗流问题的压力方程,通过常规的差分格式 (如Crank-twodash Nicolson差分格式)离散后得到的是一个五对角或七对角的线性方程组,随着网格数增加,运算量将呈级数倍增长,即使选用各种迭代算法,也很难降低计算量。为提高运算效率和计算精度,提出采用计算量较小而又无条件稳定的Douglas差分格式对交联聚合物驱数学模型进行求解。
1955年,Peaceman D W和Rachford H H提出了计算量小、具有二阶误差精度且绝对稳定的P-twodash R差分格式[18],取得了较好的计算效果并受到人们的普遍关注,但它的缺点是不能推广到三维情形(直接推广到三维是绝对不稳定的)。1962年,Douglas J提出的Douglas差分格式[19]克服了P-R格式的缺点,与P-R差分格式一样,每一时间步的计算可分解成若干个一维隐格式,只要求解具有三对角系数矩阵的方程组,从而可用追赶法求解。
假设三维抛物型方程形式如下
| $ \dfrac{{{ \partial ^2}p}}{{ \partial {x^2}}} + \dfrac{{{ \partial ^2}p}}{{ \partial {y^2}}} + \dfrac{{{ \partial ^2}p}}{{ \partial {z^2}}} = \dfrac{{ \partial p}}{{ \partial t}}$ | (15) |
对应于式(15)的Douglas差分格式为
| $ \left\{ {\begin{array}{*{20}{l}} {\dfrac{{p_{i,j,k}^{n+\frac{1}{3}}\!-\!p_{i,j,k}^n}}{{\Delta t}}\!=\! \dfrac{1}{{{h^2}}}\left[\!{\delta _x^2\left(\!{\dfrac{{p_{i,j,k}^{n+ \frac{1}{3}}\!+\!p_{i,j,k}^n}}{2}}\!\right)\!+\!\left(\!{\delta _y^2\! +\!\delta\!_z^2}\!\right)p_{i,j,k}^n}\!\right]}\\ {\dfrac{{p_{i,j,k}^{n + \frac{2}{3}} - p_{i,j,k}^{n + \frac{1}{3}}}}{{\Delta t}} = \dfrac{1}{{{h^2}}}\delta _y^2\left( {\dfrac{{p_{i,j,k}^{n + \frac{2}{3}} - p_{i,j,k}^n}}{2}}\!\right)}\\ {\dfrac{{p_{i,j,k}^{n + 1} - p_{i,j,k}^{n + \frac{2}{3}}}}{{\Delta t}} = \dfrac{1}{{{h^2}}}\delta _z^2\left( {\dfrac{{p_{i,j,k}^{n + 1} - p_{i,j,k}^n}}{2}} \right)} \end{array}} \right. $ | (16) |
为了求解压力分布,将油水相基本渗流微分方程(1)和(2)相加并写为三维的形式,推导得到只含有一个未知量
| $\begin{align} & {{B}_{\text{o}}}\cdot \text{ }\!\!\{\!\!\text{ }\frac{\partial }{\partial x}\left[ {{\lambda }_{\text{o}x}}\cdot \left( \frac{\partial {{p}_{\text{o}}}}{\partial x}-{{F}_{\text{g}}}\cdot {{\rho }_{\text{o}}}\text{g}\frac{\partial D}{\partial x} \right) \right]+\frac{\partial }{\partial y}\left[ \lambda {{}_{\text{o}y}}\cdot \left( \frac{\partial {{p}_{\text{o}}}}{\partial y}-{{F}_{\text{g}}}\cdot \rho {{}_{\text{o}}}\text{g}\frac{\partial D}{\partial y} \right) \right] \\ & +\left. \frac{\partial }{\partial z}\left[ \lambda {{}_{\text{o}z}}\cdot \left( \frac{\partial {{p}_{\text{o}}}}{\partial z}-{{F}_{\text{g}}}\cdot {{\rho }_{\text{o}}}\text{g}\frac{\partial D}{\partial z} \right) \right]+{{q}_{\text{ov}}} \right\} \\ & {{B}_{\text{w}}}\text{ }\!\!\{\!\!\text{ }\frac{\partial }{\partial x}\left[ \lambda {{}_{\text{w}x}}\cdot \left( \frac{\partial {{p}_{\text{o}}}}{\partial x}-{{F}_{\text{g}}}\cdot \rho {{}_{\text{w}}}\text{g}\frac{\partial D}{\partial x} \right) \right]+\frac{\partial }{\partial y}\left[ {{\lambda }_{\text{w}y}}\cdot \left( \frac{\partial {{p}_{\text{o}}}}{\partial y}-{{F}_{\text{g}}}\cdot \rho {{}_{\text{w}}}\text{g}\frac{\partial D}{\partial y} \right) \right] \\ & +\frac{\partial }{\partial z}\left[ \lambda {{}_{\text{w}z}}\cdot \left( \frac{\partial {{p}_{\text{o}}}}{\partial z}-{{F}_{\text{g}}}\cdot \rho {{}_{\text{w}}}\text{g}\frac{\partial D}{\partial z} \right) \right]+{{q}_{\text{wv}}}\text{ }\!\!\}\!\!\text{ }=\phi {{C}_{\text{tr}}}\cdot \frac{\partial {{p}_{\text{o}}}}{\partial t} \\ \end{align}$ | (17) |
流动系数的定义如下
| $ \lambda _{{\rm{pd}}} = F_{{\rm{Dc}}} \cdot \dfrac{{K_d K_{{\rm{rp}}} }}{{B_{\rm{p}} \mu _{\rm{p}} }}~~~~~~({\rm{p}} = {\rm{o}},{\rm{w}};{\rm{ }}d = x,y,z) $ |
对压力方程(17),按照Douglas差分格式式(16)展开即可得到相应的压力线性方程组。
首先定义如下变量
| $\begin{align} & {{T}_{\text{o}xi+\frac{1}{2}}}=\frac{\Delta {{y}_{j}}\Delta {{z}_{k}}{{K}_{xi+\frac{1}{2}}}}{\frac{1}{2}\left( \Delta {{x}_{i+1}}+\Delta {{x}_{i}} \right)}{{\left( \frac{{{F}_{\text{Dc}}}{{K}_{\text{ro}}}}{{{B}_{\text{o}}}{{\mu }_{\text{o}}}} \right)}_{i+\frac{1}{2}}}, \\ & {{T}_{\text{o}xi-\frac{1}{2}}}=\frac{\Delta {{y}_{j}}\Delta {{z}_{k}}{{K}_{xi-\frac{1}{2}}}}{\frac{1}{2}\left( \Delta {{x}_{i-1}}+\Delta {{x}_{i}} \right)}{{\left( \frac{{{F}_{\text{Dc}}}{{K}_{\text{ro}}}}{{{B}_{\text{o}}}{{\mu }_{\text{o}}}} \right)}_{i-\frac{1}{2}}}, \\ & {{T}_{\text{o}yj+\frac{1}{2}}}=\frac{\Delta {{x}_{i}}\Delta {{z}_{k}}{{K}_{yj+\frac{1}{2}}}}{\frac{1}{2}\left( \Delta {{y}_{j+1}}+\Delta {{y}_{j}} \right)}{{\left( \frac{{{F}_{\text{Dc}}}{{K}_{\text{ro}}}}{{{B}_{\text{o}}}{{\mu }_{\text{o}}}} \right)}_{j+\frac{1}{2}}} \\ & {{T}_{\text{o}yj-\frac{1}{2}}}=\frac{\Delta {{x}_{i}}\Delta {{z}_{k}}{{K}_{yj-\frac{1}{2}}}}{\frac{1}{2}\left( \Delta {{y}_{j-1}}+\Delta {{y}_{j}} \right)}{{\left( \frac{{{F}_{\text{Dc}}}{{K}_{\text{ro}}}}{{{B}_{\text{o}}}{{\mu }_{\text{o}}}} \right)}_{j-\frac{1}{2}}}, \\ & {{T}_{\text{o}zk+\frac{1}{2}}}=\frac{\Delta {{x}_{i}}\Delta {{y}_{j}}{{K}_{zk+\frac{1}{2}}}}{\frac{1}{2}\left( \Delta {{z}_{k+1}}+\Delta {{z}_{k}} \right)}{{\left( \frac{{{F}_{\text{Dc}}}{{K}_{\text{ro}}}}{{{B}_{\text{o}}}{{\mu }_{\text{o}}}} \right)}_{k+\frac{1}{2}}}, \\ & {{T}_{\text{o}zk-\frac{1}{2}}}=\frac{\Delta {{x}_{i}}\Delta {{y}_{j}}{{K}_{zk-\frac{1}{2}}}}{\frac{1}{2}\left( \Delta {{z}_{k-1}}+\Delta {{z}_{k}} \right)}{{\left( \frac{{{F}_{\text{Dc}}}{{K}_{\text{ro}}}}{{{B}_{\text{o}}}{{\mu }_{\text{o}}}} \right)}_{k-\frac{1}{2}}} \\ & {{T}_{\text{w}xi+\frac{1}{2}}}=\frac{\Delta {{y}_{j}}\Delta {{z}_{k}}{{K}_{xi+\frac{1}{2}}}}{\frac{1}{2}\left( \Delta {{x}_{i+1}}+\Delta {{x}_{i}} \right)}{{\left( \frac{{{F}_{\text{Dc}}}{{K}_{\text{rw}}}}{{{B}_{\text{w}}}{{\mu }_{\text{w}}}} \right)}_{i+\frac{1}{2}}}, \\ & {{T}_{\text{w}xi-\frac{1}{2}}}=\frac{\Delta {{y}_{j}}\Delta {{z}_{k}}{{K}_{xi-\frac{1}{2}}}}{\frac{1}{2}\left( \Delta {{x}_{i-1}}+\Delta {{x}_{i}} \right)}{{\left( \frac{{{F}_{\text{Dc}}}{{K}_{\text{rw}}}}{{{B}_{\text{w}}}{{\mu }_{\text{w}}}} \right)}_{i-\frac{1}{2}}}, \\ & {{T}_{\text{w}yj+\frac{1}{2}}}=\frac{\Delta {{x}_{i}}\Delta {{z}_{k}}{{K}_{yj+\frac{1}{2}}}}{\frac{1}{2}\left( \Delta {{y}_{j+1}}+\Delta {{y}_{j}} \right)}{{\left( \frac{{{F}_{\text{Dc}}}{{K}_{\text{rw}}}}{{{B}_{\text{w}}}{{\mu }_{\text{w}}}} \right)}_{j+\frac{1}{2}}} \\ & {{T}_{\text{w}yj-\frac{1}{2}}}=\frac{\Delta {{x}_{i}}\Delta {{z}_{k}}{{K}_{yj-\frac{1}{2}}}}{\frac{1}{2}\left( \Delta {{y}_{j-1}}+\Delta {{y}_{j}} \right)}{{\left( \frac{{{F}_{\text{Dc}}}{{K}_{\text{rw}}}}{{{B}_{\text{w}}}{{\mu }_{\text{w}}}} \right)}_{j-\frac{1}{2}}}, \\ & {{T}_{\text{w}zk+\frac{1}{2}}}=\frac{\Delta {{x}_{i}}\Delta {{y}_{j}}{{K}_{zk+\frac{1}{2}}}}{\frac{1}{2}\left( \Delta {{z}_{k+1}}+\Delta {{z}_{k}} \right)}{{\left( \frac{{{F}_{\text{Dc}}}{{K}_{\text{rw}}}}{{{B}_{\text{w}}}{{\mu }_{\text{w}}}} \right)}_{k+\frac{1}{2}}}, \\ & {{T}_{\text{w}zk-\frac{1}{2}}}=\frac{\Delta {{x}_{i}}\Delta {{y}_{j}}{{K}_{zk-\frac{1}{2}}}}{\frac{1}{2}\left( \Delta {{z}_{k-1}}+\Delta {{z}_{k}} \right)}{{\left( \frac{{{F}_{\text{Dc}}}{{K}_{\text{rw}}}}{{{B}_{\text{w}}}{{\mu }_{\text{w}}}} \right)}_{k-\frac{1}{2}}} \\ \end{align}$ |
对应于Douglas差分格式第一步的三对角形式的压力线性方程组为
| $\begin{align} & \frac{1}{2}\left( {{B}_{\text{o}}}{{T}_{\text{o}xi-\frac{1}{2}}}+{{B}_{\text{w}}}{{T}_{\text{w}xi-\frac{1}{2}}} \right)p_{\text{o}i-1,j,k}^{n+\frac{1}{3}}-\frac{1}{2} \\ & \left[ {{B}_{\text{o}}}{{T}_{\text{o}xi+\frac{1}{2}}}+{{B}_{\text{o}}}{{T}_{\text{o}xi-\frac{1}{2}}}+{{B}_{\text{w}}}{{T}_{\text{w}xi+\frac{1}{2}}}+{{B}_{\text{w}}}{{T}_{\text{w}xi-\frac{1}{2}}}+2\frac{\left( {{V}_{\text{pr}}}{{C}_{\text{tr}}} \right)_{i,j,k}^{n}}{\Delta t} \right] \\ & p_{\text{o}i,j,k}^{n+\frac{1}{3}}+\frac{1}{2}\left( {{B}_{\text{o}}}{{T}_{\text{o}xi+\frac{1}{2}}}+{{B}_{\text{w}}}{{T}_{\text{w}xi+\frac{1}{2}}} \right)p_{\text{o}i+1,j,k}^{n+\frac{1}{3}}= \\ & -\frac{1}{2}\left[ \left( {{B}_{\text{o}}}{{T}_{\text{o}xi+\frac{1}{2}}}+{{B}_{\text{w}}}{{T}_{\text{w}xi+\frac{1}{2}}} \right)\left( p_{\text{o}i+1,j,k}^{n}-p_{\text{o}i,j,k}^{n} \right)+ \right. \\ & \left. \left( {{B}_{\text{o}}}{{T}_{\text{o}xi-\frac{1}{2}}}+{{B}_{\text{w}}}{{T}_{\text{w}xi-\frac{1}{2}}} \right)\left( p_{\text{o}i-1,j,k}^{n}-p_{\text{o}i,j,k}^{n} \right) \right]+ \\ & {{F}_{\text{g}}}\cdot \text{g}\left[ \left( {{B}_{\text{o}}}{{\rho }_{\text{o}}}{{T}_{\text{o}xi+\frac{1}{2}}}+{{B}_{\text{w}}}{{\rho }_{\text{w}}}{{T}_{\text{w}xi+\frac{1}{2}}} \right)\left( {{D}_{i+1,j,k}}-{{D}_{i,j,k}} \right)+ \right. \\ & \left. \left( {{B}_{\text{o}}}{{\rho }_{\text{o}}}{{T}_{\text{o}xi-\frac{1}{2}}}+{{B}_{\text{w}}}{{\rho }_{\text{w}}}{{T}_{\text{w}xi-\frac{1}{2}}} \right)\left( {{D}_{i-1,j,k}}-{{D}_{i,j,k}} \right) \right] \\ & -\left[ \left( {{B}_{\text{o}}}{{T}_{\text{o}yj+\frac{1}{2}}}+{{B}_{\text{w}}}{{T}_{\text{w}yj+\frac{1}{2}}} \right)\left( p_{\text{o}i,j+1,k}^{n}-p_{\text{o}i,j,k}^{n} \right)+ \right. \\ & \left. \left( {{B}_{\text{o}}}{{T}_{\text{o}yj-\frac{1}{2}}}+{{B}_{\text{w}}}{{T}_{\text{w}yj-\frac{1}{2}}} \right)\left( p_{\text{o}i,j-1,k}^{n}-p_{\text{o}i,j,k}^{n} \right) \right]+ \\ & {{F}_{\text{g}}}\cdot \text{g}\left[ \left( {{B}_{\text{o}}}{{\rho }_{\text{o}}}{{T}_{\text{o}yj+\frac{1}{2}}}+{{B}_{\text{w}}}{{\rho }_{\text{w}}}{{T}_{\text{w}yj+\frac{1}{2}}} \right)\left( {{D}_{i,j+1,k}}-{{D}_{i,j,k}} \right)+ \right. \\ & \left. \left( {{B}_{\text{o}}}{{\rho }_{\text{o}}}{{T}_{\text{o}yj-\frac{1}{2}}}+{{B}_{\text{w}}}{{\rho }_{\text{w}}}{{T}_{\text{w}yj-\frac{1}{2}}} \right)\left( {{D}_{i,j-1,k}}-{{D}_{i,j,k}} \right) \right] \\ & -\left[ \left( {{B}_{\text{o}}}{{T}_{\text{o}zk+\frac{1}{2}}}+{{B}_{\text{w}}}{{T}_{\text{w}zk+\frac{1}{2}}} \right)\left( p_{\text{o}i,j,k+1}^{n}-p_{\text{o}i,j,k}^{n} \right)+ \right. \\ & \left. \left( {{B}_{\text{o}}}{{T}_{\text{o}zk-\frac{1}{2}}}+{{B}_{\text{w}}}{{T}_{\text{w}zk-\frac{1}{2}}} \right)\left( p_{\text{o}i,j,k-1}^{n}-p_{\text{o}i,j,k}^{n} \right) \right]+ \\ & {{F}_{\text{g}}}\cdot \text{g}\left[ \left( {{B}_{\text{o}}}{{\rho }_{\text{o}}}{{T}_{\text{o}zk+\frac{1}{2}}}+{{B}_{\text{w}}}{{\rho }_{\text{w}}}{{T}_{\text{w}zk+\frac{1}{2}}} \right)\left( {{D}_{i,j,k+1}}-{{D}_{i,j,k}} \right)+ \right. \\ & \left. \left( {{B}_{\text{o}}}{{\rho }_{\text{o}}}{{T}_{\text{o}zk-\frac{1}{2}}}+{{B}_{\text{w}}}{{\rho }_{\text{w}}}{{T}_{\text{w}zk-\frac{1}{2}}} \right)\left( {{D}_{i,j,k-1}}-{{D}_{i,j,k}} \right) \right] \\ & -{{B}_{\text{o}}}{{Q}_{\text{o}i,j,k}}-{{B}_{\text{w}}}{{Q}_{\text{w}i,j,k}}-\frac{\left( {{V}_{\text{pr}}}{{C}_{\text{tr}}} \right)_{i,j,k}^{n}}{\Delta t}p_{\text{o}i,j,k}^{n} \\ \end{align}$ | (18) |
对应于Douglas差分格式第二步的三对角形式的压力线性方程组为
| $\begin{align} & \left( {{B}_{\text{o}}}{{T}_{\text{o}yj-\frac{1}{2}}}+{{B}_{\text{w}}}{{T}_{\text{w}yj-\frac{1}{2}}} \right)p_{\text{o}i,j-1,k}^{n+\frac{2}{3}}- \\ & \left[ {{B}_{\text{o}}}{{T}_{\text{o}yj+\frac{1}{2}}}+{{B}_{\text{o}}}{{T}_{\text{o}yj-\frac{1}{2}}}+{{B}_{\text{w}}}{{T}_{\text{w}yj+\frac{1}{2}}}+{{B}_{\text{w}}}{{T}_{\text{w}yj-\frac{1}{2}}}+2\frac{\left( {{V}_{\text{pr}}}{{C}_{\text{tr}}} \right)_{i,j,k}^{n}}{\Delta t} \right]p_{\text{o}i,j,k}^{n+\frac{2}{3}}+ \\ & \left( {{B}_{\text{o}}}{{T}_{\text{o}yj+\frac{1}{2}}}+{{B}_{\text{w}}}{{T}_{\text{w}yj+\frac{1}{2}}} \right)p_{\text{o}i,j+1,k}^{n+\frac{2}{3}}= \\ & \left( {{B}_{\text{o}}}{{T}_{\text{o}yj+\frac{1}{2}}}+{{B}_{\text{w}}}{{T}_{\text{w}yj+\frac{1}{2}}} \right)\left( p_{\text{o}i,j+1,k}^{n}-p_{\text{o}i,j,k}^{n} \right)+ \\ & \left( {{B}_{\text{o}}}{{T}_{\text{o}yj-\frac{1}{2}}}+{{B}_{\text{w}}}{{T}_{\text{w}yj-\frac{1}{2}}} \right)\left( p_{\text{o}i,j-1,k}^{n}-p_{\text{o}i,j,k}^{n} \right)-2\frac{\left( {{V}_{\text{pr}}}{{C}_{\text{tr}}} \right)_{i,j,k}^{n}}{\Delta t}p_{\text{o}i,j,k}^{n+\frac{1}{3}} \\ \end{align}$ | (19) |
对应于Douglas差分格式第三步的三对角形式的压力线性方程组为
| $\begin{align} & \left( {{B}_{\text{o}}}{{T}_{\text{o}zk-\frac{1}{2}}}+{{B}_{\text{w}}}{{T}_{\text{w}zk-\frac{1}{2}}} \right)p_{\text{o}i,j,k-1}^{n+1}- \\ & \left[ {{B}_{\text{o}}}{{T}_{\text{o}zk+\frac{1}{2}}}+{{B}_{\text{o}}}{{T}_{\text{o}yzk-\frac{1}{2}}}+{{B}_{\text{w}}}{{T}_{\text{w}zk+\frac{1}{2}}}+{{B}_{\text{w}}}{{T}_{\text{w}zk-\frac{1}{2}}}+2\frac{\left( {{V}_{\text{pr}}}{{C}_{\text{tr}}} \right)_{i,j,k}^{n}}{\Delta t} \right] \\ & p_{\text{o}i,j,k}^{n+1}+ \\ & \left( {{B}_{\text{o}}}{{T}_{\text{o}zk+\frac{1}{2}}}+{{B}_{\text{w}}}{{T}_{\text{w}zk+\frac{1}{2}}} \right)p_{\text{o}i,j,k+1}^{n+1}= \\ & \left( {{B}_{\text{o}}}{{T}_{\text{o}zk+\frac{1}{2}}}+{{B}_{\text{w}}}{{T}_{\text{w}zk+\frac{1}{2}}} \right)\left( p_{\text{o}i,j,k+1}^{n}-p_{\text{o}i,j,k}^{n} \right)+ \\ & \left( {{B}_{\text{o}}}{{T}_{\text{o}zk-\frac{1}{2}}}+{{B}_{\text{w}}}{{T}_{\text{w}zk-\frac{1}{2}}} \right)\left( p_{\text{o}i,j,k-1}^{n}-p_{\text{o}i,j,k}^{n} \right)\quad -2\frac{\left( {{V}_{\text{pr}}}{{C}_{\text{tr}}} \right)_{i,j,k}^{n}}{\Delta t}p_{\text{o}i,j,k}^{n+\frac{2}{3}} \\ \end{align}$ | (20) |
求解方程组式(18)~式(20)即可得到油相压力分布。在此基础上,将
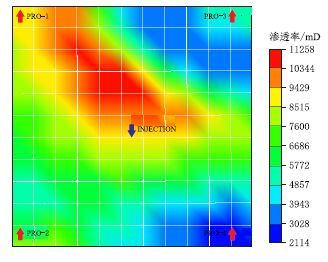
为了验证本文提出的采用Douglas格式差分渗流方程进行模型求解的优越性,选取一个五点法井网的非均质模型进行对比模拟研究,模型大小为385 m×385 m×20 m,划分为11×11×5的均匀网格系统,模型第5层渗透率场分布如图 1所示。模拟时长7 000 d,其中,在2 160~2 700 d注入2 000 mg/L的聚合物和2 000 mg/L的交联剂,注入段塞大小0.15 PV,并保持注采平衡。
 |
|
图1
模型第5层渗透率场分布
Fig. 1
Permeability distribution of the 5 |
本文基于隐式求解压力、显式求解饱和度与组分浓度的方法,采用Douglas差分格式离散化渗流数学模型,通过追赶法求解代数方程组,模拟时间为172 s。同时,在相同生产控制条件下,利用商业化的油藏数值模拟软件CMG对上述模型进行数值模拟运算,CMG软件中,采用自适应隐式方法,代数方程组采用迭代的不完全LU分解法求解,该算例模拟时间为529 s。
图 2给出了利用本文方法和CMG软件计算得到的交联聚合物驱生产动态,可以看出,两者基本吻合。计算实例表明,对于相同的油藏数值模拟问题,不同求解方法的计算效率差别很大。采用Douglas差分格式并结合追赶法能够大幅度提高模型的求解效率。
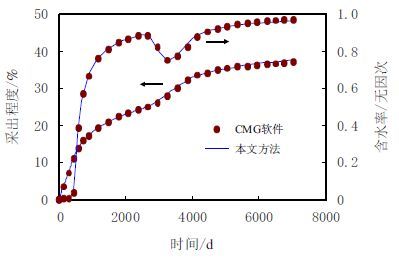 |
| 图2 采出程度和含水率随开发时间变化曲线 Fig. 2 Variation of recovery degree and water cut with the development of the reservoir |
(1)充分考虑交联聚合物驱油机理,建立了考虑因素较为完整的交联聚合物驱数学模型。
(2)基于隐式求解压力、显式求解饱和度与组分浓度的方法,在常规中心差分格式的基础上提出了求解渗流微分方程的Douglas差分格式,利用分步降维的思路求解交联聚合物驱数学模型。
(3) 计算实例表明,相比于商业化的油藏数值模拟软件 CMG,本文采用Douglas差分格式并结合追赶法求解交联聚合物驱数学模型,能够大幅度提高模型的求解效率。
符 号 说 明
t—— 时间步长,s;
g—— 重力加速度,g=9.8 m/s2;
D— 标高,m,由某一基准面算起的垂直方向深度,与重力加速度方向相同;
l—— l=P,G,Cr,聚合物、交联聚合物或交联剂组分;
a,b—— Langmuir吸附参数,与组分类型、地层水矿化度和地层岩石性质等因素有关,大小可通过实验确定;
polymer,clpolymer,Cr
n—— Cr
h—— x,y,z方向的空间步长,m;
| [1] | Sydansk R D. A newly developed chromium (Ⅲ) gel technology[J]. SPE Reservoir Engineering, 1990, 5 (3) : 346 –352. DOI:10.2118/19308-PA |
| [2] |
周志齐, 张毅. 胜利油田交联聚合物调驱技术研究及应用[J].
西安石油学院学报:自然科学版, 2000, 15 (5) : 21 –24.
Zhou Zhiqi, Zhang Yi. Study on crosslinked polymer oil displacement and its application in Shengli Oil Field[J]. Journal of Xi'an Petroleum Institure:Natural Science Edition, 2000, 15 (5) : 21 –24. |
| [3] | Moradi-Araghi A. A review of thermally stable gels for fluid diversion in petroleum production[J]. Journal of Petroleum Science and Engineering, 2000, 26 (1-4) : 1 –10. DOI:10.1016/S0920-4105(00)00015-2 |
| [4] | Alqam M H, Nasr-El-Din H A, Lynn J D. Treatment of super K-zones using gelling polymers[C]. SPE 64989, 2001. |
| [5] | Reddy B R, Eoff L, Dalrymple E D, et al. A Natural polymer-based cross-linker system for conformance gel systems[J]. SPE Journal, 2003, 8 (2) : 99 –106. DOI:10.2118/84937-PA |
| [6] |
孙志斌, 郑延欣, 李明远, 等. 交联聚合物溶液封堵多孔介质机理研究[J].
高分子材料科学与工程, 2005, 21 (2) : 225 –228.
Sun Zhibin, Zheng Yanxin, Li Mingyuan, et al. Study on mechanism of plugging porous media of linked polymer solution[J]. Polymeric Materials Science and Engineering, 2005, 21 (2) : 225 –228. |
| [7] |
马艳, 陈祖华, 李超, 等. 交联聚合物驱技术的矿场应用效果及开采特征[J].
西南石油学院学报, 2006, 28 (6) : 78 –80.
Ma Yan, Chen Zuhua, Li Chao, et al. Field application and production behavior of cross-linking polymer flooding technology[J]. Journal of Southwest Petroleum Institute, 2006, 28 (6) : 78 –80. |
| [8] |
王代流, 肖建洪. 交联聚合物微球深部调驱技术及其应用[J].
油气地质与采收率, 2008, 15 (2) : 86 –88.
Wang Dailiu, Xiao Jianhong. Application of deep-profile control and displacement technology of crosslinked polymer micro-ball system[J]. Petroleum Geology and Recovery Efficiency, 2008, 15 (2) : 86 –88. |
| [9] |
李科星, 钱志鸿, 杜金阳, 等. 交联聚合物动态成胶及运移的室内模拟研究[J].
西南石油大学学报:自然科学版, 2012, 34 (4) : 115 –121.
Li Kexing, Qian Zhihong, Du Jinyang, et al. Laboratory study on dynamic gelation behavior and transfer process of corsslinked polymer[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2012, 34 (4) : 115 –121. |
| [10] | Yuan Shiyi, Han Dong, Wang Qiang, et al. Numerical simulation study on weak gel injection[C]. SPE 64291, 2000. |
| [11] | Yuan Shiyi, Han Dong, Wang Qiang, et al. Numerical simulator for the combination process of profile control and polymer flooding[C]. SPE 64792, 2000. |
| [12] |
宋立新. 交联聚合物驱数学模型研究[J].
特种油气藏, 2003, 10 (4) : 38 –40.
Song Lixin. Mathematical model of cross-linked polymer drive[J]. Special Oil and Gas Reservoirs, 2003, 10 (4) : 38 –40. |
| [13] | Xie C J, GUAN Z L, Blunt M, et al. Numerical simulation of oil recovery after cross-linked polymer flooding[J]. Journal of Canadian Petroleum Technology, 2009, 48 (4) : 37 –41. DOI:10.2118/09-04-37 |
| [14] |
廉培庆, 同登科, 李琳琳. 高温高岩油藏交联聚合物驱研究进展[J].
精细石油化工进展, 2010, 11 (7) : 4 –7.
Lian Peiqing, Tong Dengke, Li Linlin. Development of crosslinked polymer flooding in high temperature and high salt reservoirs[J]. Advances in Fine Petrochemicals, 2010, 11 (7) : 4 –7. |
| [15] |
莫则尧, 刘兴平, 彭力田, 等. 优化和并行一个油藏数值模拟软件中的解法器[J].
石油学报, 2000, 21 (2) : 56 –61.
Mo Zeyao, Liu Xingping, Peng Litian, et al. Optimizing and paralleling a sparse liner equations solver package for reservoir simulating software[J]. Acta Petrolei Sinica, 2000, 21 (2) : 56 –61. |
| [16] | 李淑霞, 谷建伟. 油藏数值模拟基础[M]. 东营: 中国石油大学出版社, 2008 . |
| [17] |
苏雪霞, 王旭, 周亚贤, 等. 国内提高采收率用交联聚合物驱油体系研究进展[J].
精细石油化工进展, 2007, 8 (4) : 22 –25.
Su Xuexia, Wang Xu, Zhou Yaxian, et al. Research progress on improving oil recovery by using crosslinked polymer oil-displacing system in China[J]. Advances in Fine Petrochemicals, 2007, 8 (4) : 22 –25. |
| [18] | Peaceman D W, Rachford H H. The numerical solution of parabolic and elliptic differential equations[J]. Journal of the Society for Industrial and Applied Mathematics, 1955, 3 (1) : 28 –41. DOI:10.1137/0103003 |
| [19] | Douglas J, Rachford H H. On the numerical solution of heat condition problems in two and three space variables[J]. Transactions of the American Mathematical Society, 1956, 82 : 421 –439. DOI:10.1090/S0002-9947-1956-0084194-4 |
 2014, Vol. 36
2014, Vol. 36

