井壁不稳定问题是钻井工程中的世界性技术难题,也是安全高效钻井的核心问题之一。而以不稳定页岩作为目的层的页岩气储层钻长段水平井的井壁不稳定性问题更复杂、更普遍,其井壁垮塌尤为严重突出,例如,中国南方海相页岩气区硬脆性页岩储层应力环境复杂、层理/裂缝发育[1-2],水平井井壁更易垮塌。中国第一口页岩气水平井(WY201-H1 井),虽采用油基防塌钻井液体系,并逐步提高钻井液密度,但在主力页岩层段井壁垮塌仍然十分严重[3]。目前,层理性页岩气水平井井壁坍塌问题已成为制约中国页岩气勘探开发的关键问题。
为解决层理性泥页岩井壁失稳问题,国内外学者已经开展了大量的研究,研究表明层理性弱面地层对井壁稳定影响非常显著。Aadøny B S[4-6] 首先提出了各向异性地层中斜井井壁应力模型,并采用Jaeger J C 提出的单一弱面强度理论进行井壁稳定判别;Okland D 和Cook J M 开展了不同层理面夹角岩芯的厚壁圆筒实验[7],认为井壁稳定与层理性泥页岩的强度各向异性密切相关;金衍和陈勉等基于单一弱面强度理论建立了直井和斜井的井壁稳定力学模型[8-10],认为弱面地层的存在易使井壁失稳;刘向君等[11-12] 研究了岩石软弱面产状对井壁稳定性的影响;秦启荣等[13] 从力学角度模拟了结构面对井眼稳定的影响,认为结构面的存在会增大井壁失稳的风险;朱荣东等[14] 采用有限元法和孔隙弹性理论研究自然裂缝地层中的井眼行为,分析了裂缝井壁的稳定性;邓金根和蔚宝华等开展了对高陡层理性地层和页岩储层井壁稳定性理论研究及模拟试验[15-17],认为地层倾角较低情况下提高钻井液密度有利于井壁稳定,在高陡条件下提高钻井液密度不一定对井壁稳定有利。Lu Y H 和Chen M 等研究了岩石弱面在渗流作用下的井壁稳定问题[18-19]。然而,这些研究中并未针对层理性页岩储层的水平井井壁稳定问题进行深入研究,层理性地层的一大特点是有一组近于平行的层理面,一般用层理面走向、倾向和倾角描述其空间三维状态(产状),层理及其产状对井壁稳定的影响非常大,而且,层理在受到钻井液作用后的弱化作用对井壁稳定的影响也比较大,但目前对水平井状态下弱面的作用机理认识还不够清楚。为此,笔者以页岩层理对水平井井壁稳定的影响为研究对象,重点研究水平井井眼方位与页岩层理产状之间的关系和层理弱化对井壁坍塌压力的影响,从而揭示页岩气水平井井壁失稳机理及规律。
1 页岩气水平井井壁围岩应力状态对于任意水平井眼,如图 1,其井斜角为90°,井眼方位为ψ,即井眼轨迹主要受井眼方位控制,而井壁围岩应力状态受层理的产状和井眼方位综合控制。描述水平井在大地坐标(N,E,z)中的位置,可采用井深z 和井眼方位ψ;对层理产状在大地坐标(N,E,z)中的位置关系,采用层理走向北θTR 东和层理倾角θDIP 描述。由于页岩气储层一般属于硬脆性页岩,可将页岩储层视为连续线性弹性介质。为此,可建立水平井井壁围岩应力分布模型[10, 20]
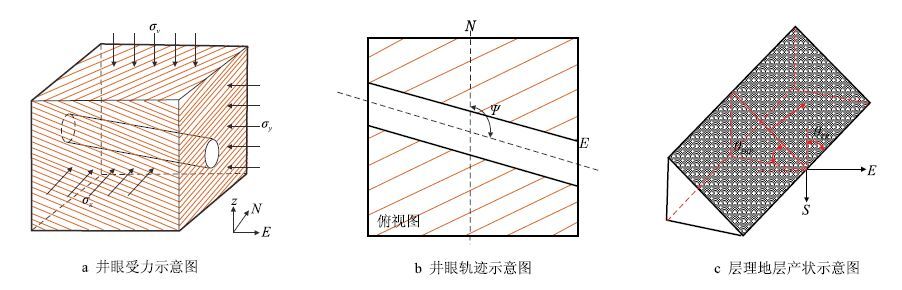 |
| 图1 层理页岩水平井井壁应力坐标关系 Fig. 1 Coordinate relations of wellbore stress of horizontal wells for shale bedding planes |
| $\left\{ \begin{array}{*{35}{l}} {{\sigma }_{\text{r}}}={{p}_{\text{m}}}-\delta \phi [{{p}_{\text{m}}}-p(r,t)] \\ {{\sigma }_{\theta }}=[(1+2\cos 2\theta ){{\cos }^{2}}\psi ]{{\sigma }_{\text{h}}}+[(1+2\cos 2\theta ){{\sin }^{2}}\psi ]{{\sigma }_{\text{H}}}\text{+} \\ (1-2\cos 2\theta ){{\sigma }_{\text{v}}}+(\xi -1){{p}_{\text{m}}}-\xi p(r,t) \\ {{\sigma }_{z}}=({{\sin }^{2}}\psi +2\nu \cos 2\theta {{\cos }^{2}}\psi ){{\sigma }_{\text{h}}}\text{+} \\ ({{\cos }^{2}}\psi +2\nu \cos 2\theta {{\sin }^{2}}\psi ){{\sigma }_{\text{H}}}-2\nu \cos 2\theta {{\sigma }_{\text{v}}}+\xi [{{p}_{\text{m}}}-p(r,t)] \\ {{\tau }_{\theta z}}=\sin 2\psi \cos \theta ({{\sigma }_{\text{H}}}-{{\sigma }_{\text{h}}}) \\ \xi =\delta [\frac{\alpha (1-2\nu )}{1-\nu }-\phi ] \\ \end{array} \right.$ | (1) |
由此,可得水平井井壁处的主应力为
| $\begin{align} & {{\sigma }_{i}}={{\sigma }_{\text{r}}}={{p}_{\text{m}}}-\delta \phi [{{p}_{\text{m}}}-p(r,t)]{{\sigma }_{j}}= \\ & \frac{({{\sigma }_{\theta }}+{{\sigma }_{z}})}{2}+\frac{1}{2}\sqrt{({{\sigma }_{\theta }}-\sigma _{z}^{2}+4\tau _{\theta z}^{2}}{{\sigma }_{k}}= \\ & \frac{({{\sigma }_{\theta }}+{{\sigma }_{z}})}{2}-\frac{1}{2}\sqrt{({{\sigma }_{\theta }}-\sigma _{z}^{2}+4\tau _{\theta z}^{2}} \\ \end{align}$ | (2) |
井壁主应力的大小,在具体计算中再排序,确定3 个主应力的大小顺序。式(2)中3 个主应力排序后,即得到页岩气水平井考虑渗流作用的井周最大、最小主应力计算模型,结合含弱面地层强度判别准则,即可求得水平井坍塌压力。其中,最大主应力与井眼轴线之间的夹角为
| $\gamma =\frac{1}{2}\arctan \frac{2{{\tau }_{\theta z}}}{{{\sigma }_{\theta }}-{{\sigma }_{z}}}$ | (3) |
层理性地层的一大特点是有一组近于平行的层理面,层理面的强度较岩石本体强度更低,常常被称为弱面。1960 年,Jaeger J C 首先提出了单一弱面强度理论[21],该理论描述了具有一条或一组平行弱面的各向同性岩体的剪切破坏,这是对摩尔-库伦(Mohr-Coulomb)破坏准则的推广。1962年,他又提出基于摩尔-库伦(Mohr-Coulomb)准则的剪切强度连续变化准则。因此,根据单一弱面强度理论,认为层理性地层岩石的破坏状态分为两种模式(如图 2 所示)。
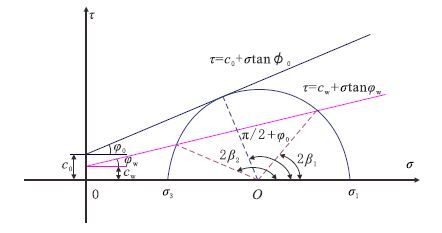 |
| 图2 含单一弱面页岩岩石强度判别模型 Fig. 2 The rock strength criterion of single weak-plane shale |
(1)当岩体不沿层理面破坏,岩体强度等于岩石本体的强度,此时,破坏面与σ1 的夹角为β0 = π/4 + φ0/2,即岩体强度为
| ${{\sigma }_{1}}={{\sigma }_{3}}+\frac{2({{c}_{0}}+{{\sigma }_{3}}\tan {{\varphi }_{0}})}{(1-\tan {{\varphi }_{0}}\cot {{\beta }_{0}})\sin 2{{\beta }_{0}}}$ | (4) |
(2)当岩体沿层理面破坏时,岩体的强度受层理强度控制,岩体的强度为
| ${{\sigma }_{1}}={{\sigma }_{3}}+\frac{2{{c}_{\text{w}}}+{{\sigma }_{3}}\tan {{\varphi }_{\text{w}}}}{(1-\tan {{\varphi }_{\text{w}}}\cot \beta )\sin 2\beta }$ | (5) |
由图 2、式(4)和式(5)可知,岩体沿层理面破坏的条件是层理面法线与第一主应力方向的夹角β 满足β1≤β≤β2。若β 满足此条件,且应力状态满足式(5)所示的关系,则岩石破坏将沿着层理面产生滑移,岩体强度受层理面强度控制;若β 不满足此条件,则岩石破坏将沿着β0 = π/4 + φ0/2 的方向破坏,岩体强度受岩石基体强度控制。其中,β1 和β2的值可通过式(6),式(7)计算
| ${{\beta }_{1}}=\frac{{{\varphi }_{\text{w}}}}{2}+\frac{1}{2}\arcsin \left[ \frac{({{\sigma }_{1}}+{{\sigma }_{3}}+2{{c}_{\text{w}}}\cot {{\varphi }_{\text{w}}})\sin {{\varphi }_{\text{w}}}}{{{\sigma }_{1}}-{{\sigma }_{3}}} \right]$ | (6) |
| ${{\beta }_{2}}=\frac{\pi }{2}+{{\varphi }_{\text{w}}}-{{\beta }_{1}}$ | (7) |
页岩水平井井眼一旦形成,地层岩石将与钻井液接触产生一系列的物理化学反应,如离子交换、渗透水化、表面水化、正压差渗透、化学渗透等作用,这些将导致岩石的强度降低,而这主要与岩石中含水量关系密切。对于层理发育的页岩,由于层理、裂隙的导流能力远高于基质,钻井液沿层理的渗透,将直接导致层理强度的弱化。页岩强度的弱化,可以看作是黏聚力和内摩擦角的变化,即c0、cw 和φ0、φw 与地层含水量有关。根据黄荣樽、陈勉的试验结果,黏聚力和内摩擦角与含水量关系为
| ${{c}_{0}}\left[ w(t) \right]={{c}_{00}}-{{a}_{1}}\left[ w(t)-{{w}_{0}} \right]$ | (8) |
| ${{\varphi }_{0}}\left[ w(t) \right]={{\varphi }_{00}}-{{b}_{1}}\left[ w(t)-{{w}_{0}} \right]$ | (9) |
| ${{c}_{\text{w}}}\left[ w(t) \right]={{c}_{\text{w}0}}-{{a}_{2}}[w(t)-{{w}_{0}}]$ | (10) |
| ${{\varphi }_{\text{w}}}\left[ w(t) \right]={{\varphi }_{\text{w}0}}-{{b}_{2}}[w(t)-{{w}_{0}}]$ | (11) |
将式(8)∼ 式(11)代入式(4)∼ 式(7)可得强度弱化后的强度判别准则。而根据前述单一弱面强度理论可知,需要确定出层理面与最大主应力间的夹角β(如图 3 所示),方可确定所采用的强度判别准则。
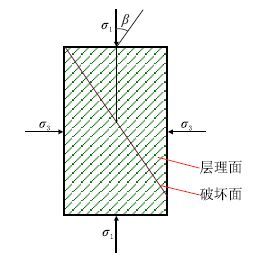 |
| 图3 层理性页岩破坏模式示意图 Fig. 3 Failure mode sketch of bedding shale |
层理的产状一般采用走向北θTR 东和倾角θDIP描述,因此,层理弱面(法线)在大地坐标(N,E,z)中的方向余弦可表示为
| $\left\{ \begin{array}{*{35}{l}} {{l}_{\text{p}}}=\frac{\tan {{\theta }_{\text{DIP}}}\cdot \tan {{\theta }_{\text{TR}}}}{\sqrt{1+{{\tan }^{2}}{{\theta }_{\text{DIP}}}(1+{{\tan }^{2}}{{\theta }_{\text{TR}}})}} \\ [10pt]{{m}_{\text{p}}}=\frac{\tan {{\theta }_{\text{DIP}}}}{\sqrt{1+{{\tan }^{2}}{{\theta }_{\text{DIP}}}(1+{{\tan }^{2}}{{\theta }_{\text{TR}}})}} \\ [10pt]{{n}_{\text{p}}}=\frac{1}{\sqrt{1+{{\tan }^{2}}{{\theta }_{\text{DIP}}}(1+{{\tan }^{2}}{{\theta }_{\text{TR}}})}} \\ \end{array} \right.$ | (12) |
而水平井井壁最大主应力σ1 在大地坐标(N,E,z)下的方向余弦可表示为
| $\left\{ \begin{array}{*{35}{l}} {{l}_{\text{m}}}=\cos \psi \cos \gamma -\sin \psi \cos \theta \\ {{m}_{\text{m}}}=\cos \psi \cos \theta +\sin \psi \cos \gamma \\ {{n}_{\text{m}}}=\sin \theta \\ \end{array} \right.$ | (13) |
从而,可以得到σ1 与层理夹角β 为
| $\beta =\arcsin \left( \frac{\left| {{l}_{\text{m}}}{{l}_{\text{p}}}+{{m}_{\text{m}}}{{m}_{\text{p}}}+{{n}_{\text{m}}}{{n}_{\text{p}}} \right|}{\sqrt{l_{\text{m}}^{2}+m_{\text{m}}^{\text{2}}+m_{\text{m}}^{\text{2}}}\sqrt{l_{\text{p}}^{\text{2}}+m_{\text{p}}^{\text{2}}+m_{\text{p}}^{\text{2}}}} \right)$ | (14) |
若式(14)得到的井壁最大主应力与层理弱面法线夹角β 满足β1≤β≤β2,则将式(2)得到的三轴主应力与式(14)得到的夹角β 代入式(5),求解非线性方程即可得到页岩气水平井钻井过程中沿层理弱面剪切破坏的坍塌压力。若夹角不满足β1≤β≤β2,则将式(2)得到的三轴主应力代入式(4),求解非线性方程得到页岩气水平井钻井过程中未沿层理弱面剪切破坏的坍塌压力。
3 页岩层理对井壁稳定的影响规律四川地区XX 井龙马溪组页岩,井深1 580 m,最大水平地应力方位为135°,最大水平地应力为46.00 MPa、最小水平地应力为28.98 MPa、上覆岩层压力为35.54 MPa、地层孔隙压力16.00 MPa,页岩层理弱面的黏聚力为5.00 MPa、页岩层理弱面的内摩擦角为23.00°,页岩岩石的黏聚力为15.00 MPa、页岩岩石的内摩擦角为40.00°,泊松比为0.23,有效应力系数为0.90,地层孔隙度为5%,地层原始含水量为3%。另外,页岩强度弱化因子根据文献[19] 确定,取页岩本体和层理的黏聚力弱化因子为28.2,取页岩本体和层理的内摩擦角弱化因子为108.4,则页岩强度弱化曲线如图 4 所示。采用上述基础数据,分别计算了层理面走向0°、30°、60° 和90°4 种情况下不同井眼轴线方位、不同层理倾角和不同含水量等因素影响下的井壁坍塌压力变化情况和分布规律(如图 5∼ 图 8 所示)。
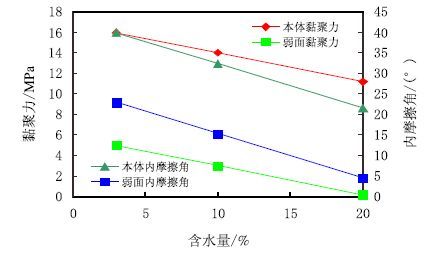 |
| 图4 页岩强度弱化曲线 Fig. 4 Strength attenuation curve of shale |
(1) 对于页岩层理无弱化的情况,即页岩中含水量为原始含水量(w0=3%)时,如图 5a∼ 图 8a 所示。当层理倾角0° <θDIP <15° 时,层理性页岩地层井壁坍塌压力受地层走向和井眼方位的影响较小,坍塌压力整体上比较高,井眼稳定性整体上较差,沿最小水平地应力方向(45° 或225°)钻进稳定性相对较好,沿最大水平地应力方向(135° 或315°)钻进稳定性相对差,二者之间整体差异较小;当层理倾角90°>θDIP>75° 时,在层理性页岩地层中沿不同方位钻进水平井,井壁坍塌压力变化幅度最大,沿着层理弱面倾斜方向钻进的井眼稳定性最好,沿最小水平地应力方向钻进稳定性较好,沿最大水平地应力方向钻进稳定性最差,三者之间整体差异较大;当层理倾角15°<θDIP <75° 时,沿最小水平地应力方向钻进稳定性最好,沿最大水平地应力方向钻进稳定性最差,其中,在θDIP=45° 情况下沿最大水平地应力方向钻进是所有情况中最不利于井眼稳定的;整体上,沿着最小水平地应力方向附近钻进井眼稳定性较好,而且,随着层理弱面走向增加,最小水平地应力方向附近利于稳定的钻进方位角度范围逐渐降低。由此不难看出,页岩层理产状是影响页岩气水平井井壁坍塌失稳的重要因素之一,而井壁坍塌压力变化规律仍然受原地应力控制。
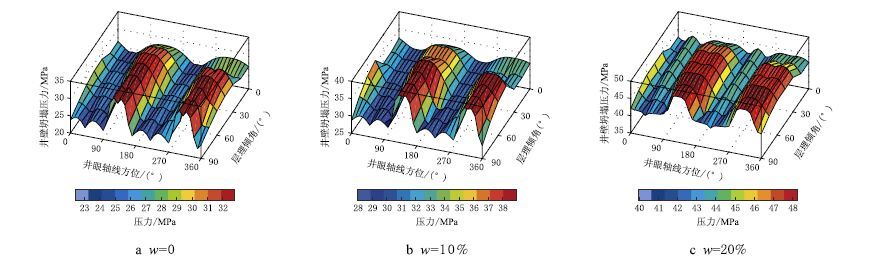 |
| 图5 θTR=0° 时井壁坍塌压力变化规律 Fig. 5 The change rule of collapse pressure at θTR=0° |
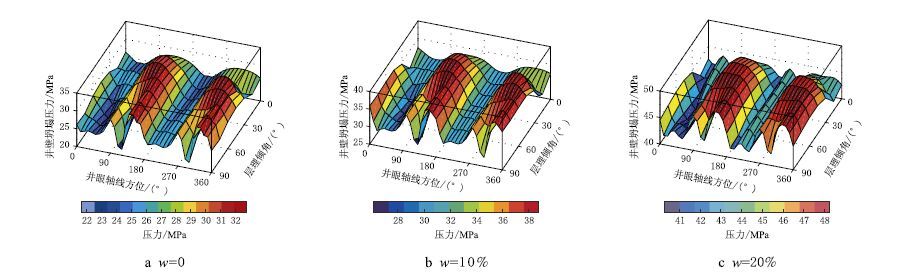 |
| 图6 θTR=30° 时井壁坍塌压力变化规律 Fig. 6 The change rule of collapse pressure at θTR=30° |
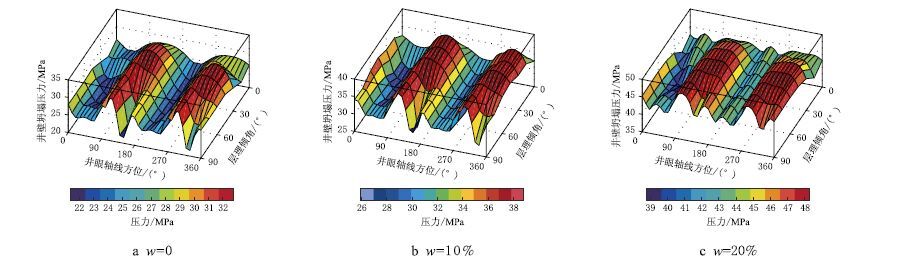 |
| 图7 θTR=60° 时井壁坍塌压力变化规律 Fig. 7 The change rule of collapse pressure at θTR=60° |
(2) 无论页岩地层层理产状如何变化,随着页岩强度弱化程度(含水量w)的增加,页岩地层井壁坍塌压力迅速增加,如图 5∼ 图 8 所示。对于不同层理产状,井壁坍塌压力随井眼方位、层理面走向和层理面倾角的变化幅度大约为3.9∼12.5 MPa;当含水量增加至10% 时,由于层理弱化所产生的井壁坍塌压力增幅大约为4.3∼7.5 MPa,其增幅为17.67%∼31.94%;当含水量增加至20% 时,由于层理弱化所产生的井壁坍塌压力增幅大约为13.92∼22.62 MPa,其增幅为43.45%∼100.73%;同时,随着层理面弱化程度的增加,不同层理产状和井眼方位组合下的井壁坍塌压力分布规律略有差异:含水量w <10% 时的分布规律与未弱化时大致相同;含水量10%<w<20% 时的分布规律略有不同,集中表现为井壁坍塌压力变化幅度更大,利于井眼稳定的钻进方位范围逐渐缩小,即由于层理面强度参数受弱化影响,导致井壁岩石沿层理面破坏的夹角范围逐渐变宽。显然,页岩层理弱化是导致页岩气水平井井壁坍塌失稳的重要影响因素。
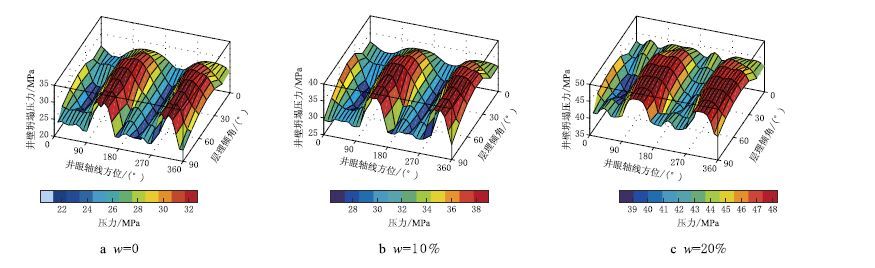 |
| 图8 θTR=90° 时井壁坍塌压力变化规律 Fig. 8 The change rule of collapse pressure at θTR=90° |
对于受地层层理面产状、井眼方位控制的井壁坍塌压力变化,可以通过优化井眼轨道方位确定合理的钻进方位(即井眼方位),从坍塌压力较低有利于井壁稳定的方向钻水平井,这对解决井壁稳定问题是一个非常重要的手段。而对于受页岩地层层理面弱化所导致的井壁坍塌问题,仅仅采用优化井眼轨道方位这些纯力学的手段已经不能很好地解决井壁坍塌问题,必须结合页岩理化性能、岩石力学性能,尤其是层理弱面的力学性能、水化致弱、压力传递等多方面进行综合分析,方可有效地解决井壁坍塌问题。
4 结论(1)以线性弹性井壁稳定力学模型和单一弱面强度理论为基础,建立了层理性页岩水平井井壁稳定模型,模型综合考虑了页岩层理产状、层理弱面强度、岩石强度、水平井井眼方位、强度弱化(含水量w)等因素的影响。
(2)层理性页岩地层井壁坍塌压力与层理面产状和井眼方位关系密切,即页岩层理产状是影响页岩气水平井井壁坍塌失稳的重要因素之一。当井壁坍塌压力随井眼方位、层理面走向和层理面倾角的变化幅度大约为3.9∼12.5 MPa,90°>θDIP>75° 情况下沿最小水平地应力方向和层理弱面倾斜方位钻进井眼最稳定,0° <θDIP<15° 情况下沿任意方向钻进稳定性差异较小,15°<θDIP<75° 情况下沿最小水平地应力方向钻进井眼稳定性较好、沿最大地应力方向钻进井眼稳定性最差,θDIP=45° 情况下的坍塌压力最高、井眼稳定性最差。
(3)页岩层理弱化是导致页岩气水平井井壁坍塌失稳的一个重要影响因素,无论页岩地层层理产状如何变化,随着层理面弱化程度(含水量w)的增加,页岩地层井壁坍塌压力迅速增加,由于层理弱化所产生的井壁坍塌压力增幅大约为4.30∼22.62 MPa,当含水量w 为20% 时坍塌压力增幅可达一倍以上。
(4) 对于层理性页岩水平井钻井,在设计井眼钻进方位时,需要综合考虑层理面产状、页岩强度弱化、页岩理化性能、岩石本体力学性能、泥浆化学和压力传递等因素的影响,确定合理的防塌措施,从而解决页岩气水平井井壁严重坍塌问题。
符号说明σr,σθ,σz,τθz—井眼圆柱坐标下井壁应力分量,MPa;
σH—水平最大地应力,MPa;
σh—水平最小地应力,MPa;
σv—垂向地应力,MPa;
pm—钻井液液柱压力,MPa;
p(r,t)—地层孔隙压力,MPa;
δ—渗透系数,无因次,当井壁不可渗透时δ=0,当井壁渗透时δ=1;
θ—井周角,(°)
ψ—方位角(井眼轴线与最大水平地应力方位夹角),(°);
ν—泊松比,无因次;
ξ—渗流效应系数,小数;
α—有效应力系数,无因次;
$\phi $—地层孔隙度,%;
σi,σj,σk—井壁的3 个主应力,MPa;
γ—最大主应力σ1 与井眼轴线之间的夹角,(°);
σ1—最大主应力,MPa;
σ3—最小主应力,MPa;
c0—岩石本体的黏聚力,MPa;
φ0—岩石本体的内摩擦角,(°);
c00—岩石本体原始黏聚力,MPa;
φ00—岩石本体原始内摩擦角,(°);
cw—岩石层理面的黏聚力,MPa;
φw—岩石层理面的内摩擦角,(°);
cw0—层理面的初始黏聚力,MPa;
φw0—层理面的初始内摩擦角,(°);
a1,a2—黏聚力弱化因子,无因次;
b1,b2—内摩擦角弱化因子,无因次;
w0—地层原始含水量,%;
w(t)—t 时刻地层含水量,%;
lp,mp,np—层理弱面法线在大地坐标(N,E,z)中的方向余弦;
θDIP—层理面倾角,(°);
θTR—层理面走向,(°);
lm,mm,nm—井壁最大主应力在大地坐标(N,E,z)中的方向余弦;
β—井壁最大主应力与层理弱面夹角,(°)。
| [1] |
王华平, 张铎, 张德军, 等. 威远构造页岩气钻井技术探讨[J].
钻采工艺, 2012, 35 (2) : 9 –11.
Wang Huaping, Zhang Duo, Zhang Dejun, et al. Drilling technologies on shale gas in weiyuan structure[J]. Drilling & Production Technology, 2012, 35 (2) : 9 –11. |
| [2] |
王怡, 徐江, 梅春桂, 等. 含裂缝的硬脆性泥页岩理化及力学特性研究[J].
石油天然气学报, 2011, 33 (6) : 104 –108.
Wang Yi, Xu Jiang, Mei Chungui, et al. Chemical and mechanical properties of brittle fractured mud shale[J]. Journal of Oil and Gas Technology, 2011, 33 (6) : 104 –108. |
| [3] |
何涛, 李茂森, 杨兰平, 等. 油基钻井液在威远地区页岩气水平井中的应用[J].
钻井液与完井液, 2012, 29 (3) : 1 –5.
He Tao, Li Maosen, Yang Lanping, et al. Application of oil-based drilling fluid in shale gas horizontal well in district of weiyuan[J]. Drilling Fluid & Completion Fluid, 2012, 29 (3) : 1 –5. |
| [4] | Aadøny B S. Modeling of the stability of highly inclined boreholes in anisotropic rock formations[J]. SPE Drilling Engineering, 1988, 3 (3) : 259 –268. DOI:10.2118/16526-PA |
| [5] | Aadøny B S, Chenevert M E. Stability of highly inclined boreholes[J]. SPE Drilling Engineering, 1987, 2 (4) : 364 –374. DOI:10.2118/16052-PA |
| [6] | Aadøny B S. Effects of reservoir depletion on borehole stability[J]. Journal of Petroleum Science and Engineering, 1991, 6 (1) : 57 –61. DOI:10.1016/0920-4105(91)90024-H |
| [7] | Okland D,Cook J M. Bedding-related borehole instability in high-angle wells[C]. SPE 47285, 1998. |
| [8] |
金衍, 陈勉, 陈治喜, 等. 弱面地层的直井井壁稳定力学模型[J].
钻采工艺, 1999, 22 (3) : 13 –14.
Jin Yan, Chen Mian, Chen Zhixi, et al. Mechanics model of sidewall stability of straight wells drilled through weakly consolidated formations[J]. Drilling & Production Technology, 1999, 22 (3) : 13 –14. |
| [9] |
金衍, 陈勉, 柳贡慧, 等. 弱面地层斜井井壁稳定性分析[J].
石油大学学报:自然科学版, 1999, 23 (4) : 33 –35.
Jin Yan, Chen Mian, Liu Gonghui, et al. Anlysis on borehole stability of weak-face formation in directional well[J]. Journal of the University of Petroleum, China, 1999, 23 (4) : 33 –35. |
| [10] |
金衍, 齐自立, 陈勉, 等. 水平井试油过程裂缝性储层失稳机理[J].
石油学报, 2011, 32 (2) : 295 –298.
Jin Yan, Qi Zili, Chen Mian, et al. A mechanism study on the fractured reservoir instability during well testing of horizontal wells[J]. Acta Petrolei Sinica, 2011, 32 (2) : 295 –298. |
| [11] |
刘向君, 陈一健, 肖勇. 岩石软弱面产状对井壁稳定性的影响[J].
西南石油学院学报, 2001, 23 (6) : 12 –13.
Liu Xiangjun, Chen Yijian, Xiao Yong. Effect of weakplane dip angle and dip azimuth angle on wellbore stability[J]. Journal of Southwest Petroleum Institute, 2001, 23 (6) : 12 –13. |
| [12] |
刘向君, 叶仲斌, 陈一健. 岩石弱面结构对井壁稳定性的影响[J].
天然气工业, 2002, 22 (2) : 41 –42.
Liu Xiangjun, Ye Zhongbin, Chen Yijian. Influence of rock weak plane texture on sidewall stability[J]. Natural Gas Industry, 2002, 22 (2) : 41 –42. |
| [13] |
秦启荣, 邓辉. 裂缝对石油井壁力学稳定性影响[J].
西南石油大学学报, 2007, 29 (4) : 167 –170.
Qin Qirong, Deng Hui. Influence of rock fractureson me-chanical stability of well-wall[J]. Journal of Southwest Petroleum University, 2007, 29 (4) : 167 –170. |
| [14] |
朱荣东, 陈平, 夏宏泉, 等. 裂缝井壁力学稳定性研究[J].
断块油气田, 2007, 14 (5) : 56 –58.
Zhu Rongdong, Chen Ping, Xia Hongquan, et al. Study on stability of fractured borehole wall[J]. Fault-Block Oil & Gas Field, 2007, 14 (5) : 56 –58. |
| [15] |
蔚宝华, 闫伟, 李斌, 等. 高陡层理性地层井壁稳定性模拟试验研究[J].
石油钻采工艺, 2009, 31 (2) : 48 –50.
Yu Baohua, Yan Wei, Li Bin, et al. Mechanical borehole stability test study in highly-dipped laminated formation[J]. Oil Drilling & Production Technology, 2009, 31 (2) : 48 –50. |
| [16] |
袁俊亮, 邓金根, 蔚宝华, 等. 页岩气藏水平井井壁稳定性研究[J].
天然气工业, 2012, 32 (9) : 66 –70.
Yuan Junliang, Deng Jin'gen, Yu Baohua, et al. Wellbore stability of horizontal wells in shale gas reservoirs[J]. Natural Gas Industry, 2012, 32 (9) : 66 –70. |
| [17] |
赵凯, 邓金根, 蔚宝华, 等. 层理性泥页岩大斜度井井壁稳定性研究[J].
科学技术与工程, 2013 (5) : 1147 –1149.
Zhao Kai, Deng Jin'gen, Yu Baohua, et al. Borehole stability of highly-deviated well in bedding shale[J]. Science Technology and Engineering, 2013 (5) : 1147 –1149. |
| [18] | Lu Y H, Chen M, Jin Y, et al. A mechanical model of borehole stability for weak plane formation under porous flow[J]. Petroleum Science and Technology, 2012, 30 (15) : 1629 –1638. DOI:10.1080/10916466.2010.514583 |
| [19] | Lu Y H, Chen M, Jin Y, et al. Influence of porous flow on wellbore stability for an inclined well with weak plane formation[J]. Petroleum Science and Technology, 2013, 31 (6) : 616 –624. DOI:10.1080/10916466.2011.601505 |
| [20] | Yang Z S, Ma T S, Chen P, et al. Derivation of the coordinate and the stress components transformation equation in wellbore stability mechanics analysis[A]//Mechanical Engineering and Material Science[C]. Shanghai, China, 2012:742-745. |
| [21] | Jaeger J C. Shear failure of anistropic rocks[J]. Geological Magazine, 1960, 97 (1) : 65 –72. DOI:10.1017/S0016756800061100 |
 2014, Vol. 26
2014, Vol. 26

