2. 中国石油西南油气田分公司, 四川 成都 610051
2. Southwest Oil & Gas Field Company, PetroChina, Chengdu, Sichuan 610051, China
天然气压缩机(简称压缩机)是石油化工行业用于天然气、石油气及液化气等的回收、集气及增压、输送等作业的关键设备,其运行的安全性一直是使用及管理者十分关注的问题,特别是处于寿命后期及超期服役机组能否安全运行成为关注的重点,目前国内外尚无一套有效的方法用于压缩机组的安全性能评价。故研究压缩机组整体性评价方法及建立相应的判废标准,可为机组判废、降级使用及换件等安全管理提供理论基础及科学依据。
往复式压缩机一般由动力部分、压缩部分及辅助系统组成,在对机组整体评价时主要从安全性和经济性指标进行分析,在确定各部件的综合评价结果之后,利用其在机组系统中所占权重进行机组整体评价。本文用层次分析法建立具有安全性和经济性两个评价准则的压缩机各部件的权重评价方法[1-2],评价时需确定两个关键性问题:一是建立压缩机整体评价体系,二是确定压缩机各部件权重系数。其特点是,安全性指标的评价具有模糊特性,经济性评价可由压缩机制造厂给出,具有确定性;利用层次分析法确定压缩机各部件在压缩机评价中的权重,使安全性和经济性评价指标具有满意的一致性,从而得出各部件的权重因子评价指标。
1 层次分析法原理及其步骤 1.1 层次分析法原理层次分析法(The Analytic Hierarchy Process,简称AHP)[3-4] 是Saaty T L 于20 世纪80 年代中期提出的一种系统分析方法,是一种将定性问题进行定量分析较实用的多准则、多目标的决策方法,它模仿人们对复杂决策问题的思维、判断过程进行构造,将决策者的思维过程数量化,把人的主观判断用数量形式表达和处理,本质上讲是一种思维方式并具有高度的逻辑性、系统性、间接性和实用性等特点[5-7]。
AHP 是确定多因素复杂问题中各要素权重的一种实用方法[8-10],它将所研究的复杂问题看作一个系统,根据系统涉及的因素和要达到的目标,通过对系统内的因素及其相互关系分析,划出各因素相互联系的有序层次结构体系,再对结构体系中的每一层次按某一给定的准则,请相关专家进行判断确定每一层次各因素逐对比较,相应给出各因子相对重要性的定量分析,建立数学模型,计算每一层次全部的相对重要性权重,并加以排序,最后根据排序结果进行决策和确定选择解决问题的措施[11-13]。
1.2 层次分析法步骤层次分析法将复杂问题分解为各个组成因素,再将这些因素按支配关系分成若干组,形成有序的递阶层次结构,通过两两比较的方式确定层次中的诸因素相对重要性总排序,即分解、判断、综合要经过建立递阶层次结构、构造两两比较矩阵、计算各要素的权重、计算当前一层元素关于总的目标的排序权重并做一致性检验[14]。
层次分析法的一般步骤是:(1)根据待评价对象权重因素构建递阶层次评价指标体系,建立问题层次结构模型;(2)在多级递阶结构模型中,同一级要素根据结构标度准则两两比较后确定其重要度并构造判断矩阵;(3)计算评价指标各项权重并得出各判断矩阵最大特征值${\lambda _{\max }}$;(4)层次单排序及其一致性检验;(5)层次总排序及其一致性检验。
2 应用层次分析法确定天然气压缩机各部件权重根据AHP 的基本思想,专家填写判断矩阵的各项指标符合给定的要求时,可根据以下过程确定评价指标的权重集[15-16],评价指标用层次分析法确定权重的计算过程如图 1。
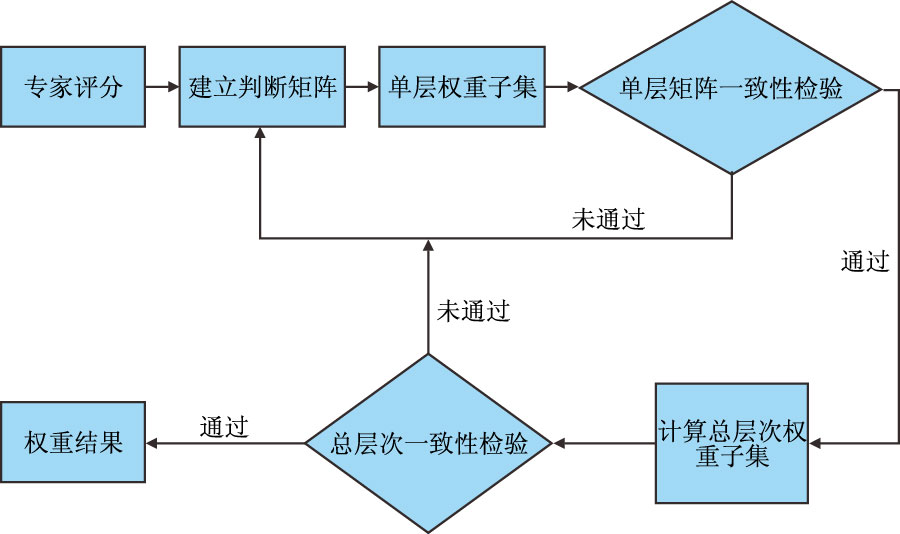 |
| 图1 层次分析法确定权重过程 Fig. 1 The process to determine the weight by AHP |
由天然气压缩机评价中确定各部件权重的基本方案,首先确定天然气压缩机各部件权重评价指标体系、构造出层次结构模型、建立两两比较矩阵、确定单层权重和总层次权重并进行一致性检验,确定各部件在机组系统中所占权重因子。
2.1 天然气压缩机整体性能评价指标体系天然气压缩机整体评价主要目的是评判压缩机当前安全状况处于其全生命周期的具体阶段,当机组寿命达到一定程度时对机组进行报废,即机组运行存在较大安全性威胁或其自身经济性(更换部件、维修保养费用及因事故影响产量等造成)指标达到规定值时判为报废;当机组整体性能评价结果为具有一定风险时需对机组降级使用或更换某些部件以确保机组安全运行。在对机组整体评价时需先对各部件进行分析并确定其自身评价结果,利用层次分析法确定各部件的权重因子,进而得出机组整体评价结果。
层次分析法目标层为确定天然气压缩机各部件权重,准则层主要包括安全性判断矩阵${\textbf{C}}_1$和经济性判断矩阵${\textbf{C}}_2$,评价对象为:曲轴、、活塞杆、连杆、连接螺栓、机身、中体、飞轮、缸体、缸盖、活塞、十字头、余隙缸体、轴承、风扇叶片、空冷器、缓冲罐、分离器、工艺气管道、仪控系统及润滑系统共20 个部件,已知某型机组中缸体4 个、缸盖4 个、十字头4 个、轴承3 个、缓冲罐4 个、中体2 个、分离器2 个,在确定判断矩阵时根据专家评分结果进行计算,最后确定具体单个部件的权重值。
2.2 构造层次结构模型在确定天然气压缩机整体评价指标体系之后,将问题所包含的因素划分为目标层、准则层和评价对象层[17],用层次分析法确定压缩机各部件权重因子建立递阶层次关系如图 2。
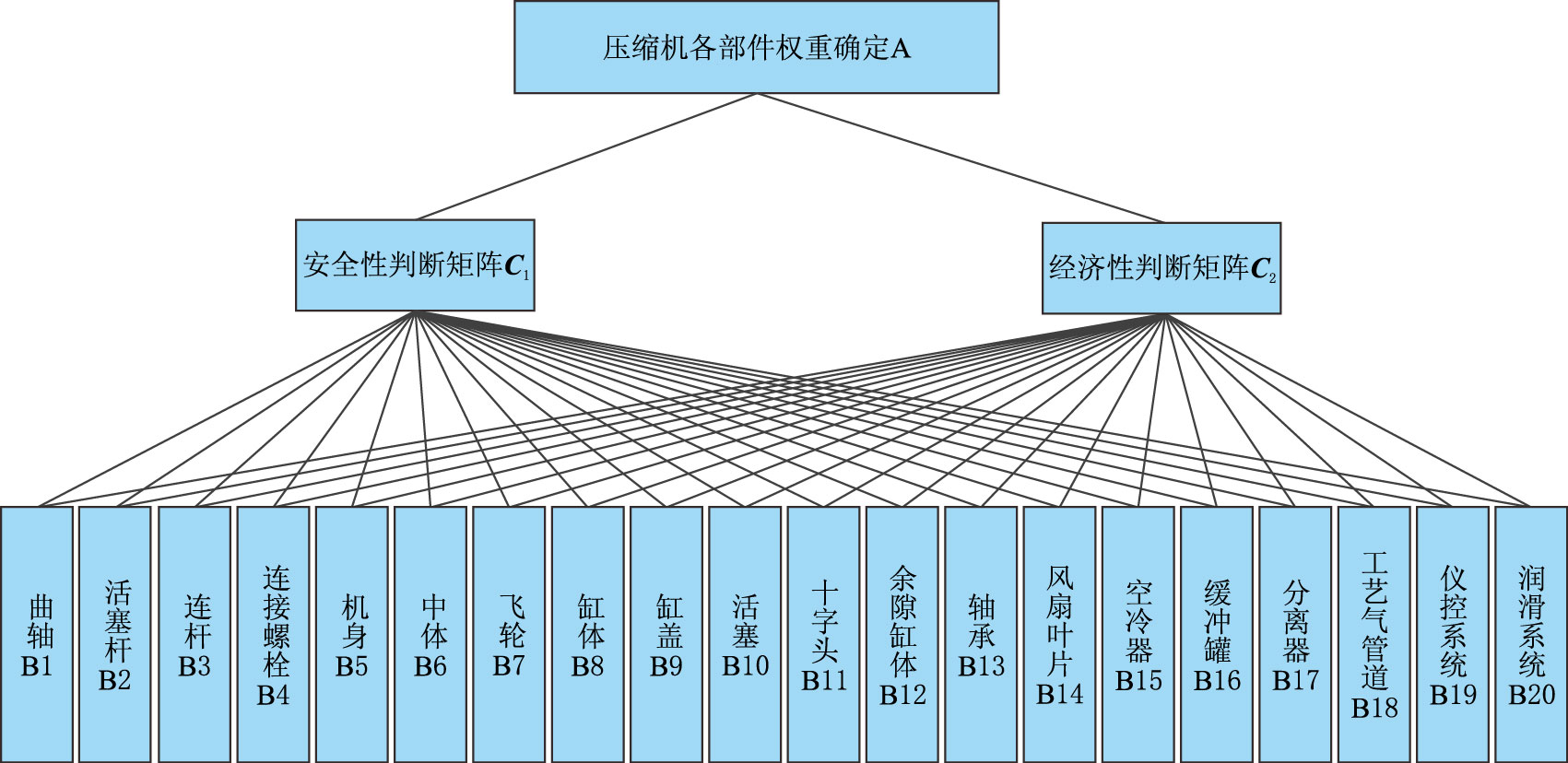 |
| 图2 压缩机各部件权重递阶层次结构图 Fig. 2 The hierarchical structure diagram of various compressor components weight |
评价层次结构模型确定之后,上下层次指标之间的隶属关系就被确定了,对同一层次指标进行两两比较,其比较结果以1∼9 标度法表示,各级标度的含义见表 1。
| 表1 判断矩阵标度及其含义 Table 1 The scale and meaning of judgement matrix |
设有n个评价对象$x = \left\{ {{x_1},{x_2}, \cdots ,{x_n}} \right\}$ 对目标层的权重,首先确定他们所在准则层中所占比重,每次取两个因素成对比较,即以${a_{ij}}$表示${x_i}$和${x_j}$对所在准则层的影响之比,将专家评价结果经过两两比较之后按矩阵标度表示为如下评价指标体系,确定比较判断矩阵${\textbf{A}}$为
| ${\textbf{A}}= \left[ {\begin{array}{*{20}{c}} 1 & {{a_{12}}} & {{a_{13}}} & \cdots & {{a_{1n}}}\\ {{a_{21}}} & 1 & {{a_{23}}} & \cdots & {{a_{2n}}}\\ {{a_{31}}} & {{a_{32}}} & 1 & \cdots & {{a_{3n}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {{a_{n1}}} & {{a_{n2}}} & {{a_{n3}}} & \cdots & 1 \end{array}} \right]$ | (1) |
对于同一层次n个指标,得到的两两比较判断矩阵${\textbf{A}} = \left\{ {{a_{ij}}} \right\}$ ,判断矩阵中的值应满足下列条件:(1) 正互反性:${a_{ij}} > 0,{a_{ij}} = \dfrac{1}{{{a_{ji}}}},{a_{ii}} = 1$;(2) 一致性:${a_{ij}}${⋅}${a_{jk}} = {a_{ik}}$,$i,j,k = 1,2, ${$\cdots$}$,n$。满足上述条件的正互反矩阵${\textbf{A}}$为一致性矩阵。
2.4 层次单排序及其一致性检验单一层次排序需要确定判断矩阵特征向量和最大特征值,根据层次分析法判断矩阵的定义,判断矩阵最大特征值与其他特征值的比较相差很大时适宜用方根法[18],若判断矩阵满足一致性条件,则其最大特征值应为其判断矩阵的阶数,可根据判断矩阵的具体情况选用不同的算法。
2.4.1 层次单排序用方根法计算评价指标权重(1) 计算判断矩阵${\textbf{A}}$的每一行元素的积${M}$:${M_i} = \prod\limits_{j = 1}^n {{a_{ij}},i = 1,2, \cdots ,n} $。
(2) 计算各行${M_i}$的n次方根值${\overline w_i} = \sqrt[n]{{{M_i}}},i = 1,2, \cdots ,n$,其中,n-矩阵阶数。
(3) 将向量${\left[ {\begin{array}{*{20}{c}} {{w_1}}&{{w_2}}& \cdots &{{w_n}} \end{array}} \right]^{\rm{T}}}$归一化,${w_i} = {\overline w _i}/\sum\limits_{i = 1}^n {{{\overline w }_i}}$。
2.4.2 计算判断矩阵A的最大特征值判断矩阵A的最大特征值为
| ${\lambda _{\max }} = \sum\limits_{i = 1}^n {\dfrac{{{{({\textbf{A}}\cdot w)}_i}}}{{n{w_i}}}}$ | (2) |
式中:
${\lambda _{\max }}$-判断矩阵${\textbf{A}}$的最大特征值;
${w_i}$—各项指标权重,%。
2.4.3 单层次一致性检验检验判断矩阵是否具有满意一致性需计算单层一致性指标$C_{\rm{I}} = \dfrac{{{\lambda _{\max }} - n}}{{n - 1}}$,${\lambda _{\max }}$通过上述计算可得;判断矩阵平均随机一致性指标${R_{\rm{I}}}$ 通过查表获得[19],对于1∼15 阶判断矩阵${R_{\rm{I}}}$ 如表 2,判断矩阵一致性比率为$C_{\rm{R}} = \dfrac{{C_{\rm{I}}}}{{R_{\rm{I}}}}$ ;当${C_{\rm{R}}} = 0$ 时,${\textbf{A}}$具有完全一致性;当$C_{\rm{R}} < 0.1$ 时,即认为判断矩阵具有满意的一致性,否则需要调整判断矩阵使其达到可接受的一致性比率[20]。
| 表2 平均随机一致性指标${R_{\rm{I}}}$ 值 Table 2 The ${R_{\rm{I}}}$ values of average random consistency index |
层次总排序为其最底层所有指标相对于总目标的权重向量,需要进行多层次的组合计算[21-22],假如第k 层组合权重$w^k$ 由本层(n 个指标)的相对权重$R^k$与上一层(设有m 个指标)的组合权重$w^{k-1}$的乘积求得,即
| ${w^k} = {R^k}{w^{k - 1}} = \left[ {\begin{array}{*{20}{c}} {w_{11}^k} & {w_{12}^k} & \cdots & {w_{1m}^k}\\ {w_{21}^k} & {w_{22}^k} & \cdots & {w_{2m}^k}\\ \vdots & \vdots & \vdots & \vdots \\ {w_{n1}^k} & {w_{n2}^k} & \cdots & {w_{nm}^k} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {w_1^{k - 1}}\\ {w_2^{k - 1}}\\ \vdots \\ {w_m^{k - 1}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\sum\limits_{j = 1}^m {w_{1j}^kw_j^{k - 1}} }\\ {\sum\limits_{j = 1}^m {w_{2j}^kw_j^{k - 1}} }\\ \vdots \\ {\sum\limits_{j = 1}^m {w_{nj}^kw_j^{k - 1}} } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {w_1^k}\\ {w_2^k}\\ \vdots \\ {w_m^k} \end{array}} \right]$ | (3) |
式中:
${w^k}$-第k层的各指标对于总目标的组合权重,%;
$w_{ij}^k$-针对某项评价指标的第k层的第i行,j列的权重,%。
依次由上而下逐层叠加即可得出所有层次目标的总排序值,当k=1 时就是第一准则层对应总目标的相对权重集。对总排序结果进行一致性检验,也需要进行多层次的组合计算[23-24]。假如第k层的第j个元素的一致性指标${C_{\rm{I}}}_j^k$,${R_{\rm{I}}}_j^k$和${C_{\rm{R}}}_j^k$,j=1,2,…,m,则第k层综合性检验指标
| $C_{\rm{R}}{^k} = \dfrac{{C_{\rm{I}}{^k}}}{{R_{\rm{I}}{^k}}}$ | (4) |
式中:
$C_{\rm{R}}{^k}$-第k层综合性比率;
$C_{\rm{I}}{^k}$-第k层一致性指标;
$R_{\rm{I}}{^k}$-第k层判断矩阵平均随机一致性指标;其中,$C_{\rm{I}}{^k} = \sum\limits_1^m {{C_{\rm{I}}}_j^k} {w^{k - 1}}$;${R_{\rm{I}}}{^k} = \sum\limits_1^m {{R_{\rm{I}}}_j^k} {w^{k - 1}}$。
当$C_{\rm{R}}{^k}$<0.1时,认为判断矩阵的整体一致性是可以接受的;当${C_{\rm{R}}} \geqslant 0.1$时,具有非满意一致性,应予以调整或舍弃不用。
3 案例分析依照上述计算权重的方法,以西南油气田某增压站整体往复式天然气压缩机组ZTY265 为例,该机组已连续使用接近25 a,各项指标特征显示均能够正常运行,但已达到设计寿命,且在正常运行过程中偶有事故发生,在对该达到设计运行寿命的机组能否继续使用、仍能使用多久以及什么条件下报废进行评价,在进行评价过程中,用层次分析法确定该型机组各部件权重系数以建立压缩机组整体评价方法。
3.1 根据建立递阶层次评价指标体系,构建两两判断矩阵聘请有关专家自上而下对天然气压缩机各层次指标进行两两重要程度判断比较,构造判断矩阵。为了对各因素之间进行两两比较,得到量化的判断矩阵,根据天然气压缩机设计厂家、制造厂家、管理人员、操作人员及维护人员评分得各级判断矩阵。
3.1.1 一级指标判断矩阵根据部件安全性及经济性重要性专家评分,结合标度法两两比较建立一级判断矩阵A,如表 3所示。
| 表3 一级判断矩阵${\textbf{A}}$ Table 3 The first level judgment matrix ${\textbf{A}}$ |
(1)安全性指标判断矩阵
根据建立的递阶层次评价体系,结合专家对部件安全性和经济性评分结果,根据层次分析法标度准则建立二级判断矩阵,部件安全性指标${\textbf{C}}_1$判断矩阵如表 4。该矩阵满足正互反性条件,且矩阵对角线数据为部件自身的比较所以值均为1。矩阵一致性要求需要对待评价部件判断矩阵特征解进行一致性检验,以确定建立的判断矩阵是否符合层次分析法确定权重的合理性要求。
| 表4 二级安全性指标判断矩阵 Table 4 The second level safety indicators judgment matrix |
(2)经济性指标判断矩阵
根据建立的递阶层次评价体系,综合考虑部件本身成本、设计制造等因素,依据压缩机部件自身经济及附加价值,建立部件考虑经济性评价指标的判断矩阵${\textbf{C}}_2$ 如表 5 所示。与安全性判断矩阵一样该矩阵明显满足正互反性条件,且矩阵对角线数据均为1。矩阵一致性要求需要对判断矩阵特征解进行单层次和总层次一致性检验,以确定建立的判断矩阵是否符合层次分析法确定权重的合理性要求。
| 表5 二级经济性指标判断矩阵 Table 5 The second level economic indicators judgment matrix |
根据层次分析法确定部件权重的方法,首先建立一级指标判断矩阵${\textbf{A}}$并计算其特征向量及权重。
| ${\textbf{A}} = \left[ {\begin{array}{*{20}{c}} {{a_{11}}} & {{a_{12}}}\\ {{a_{21}}} & {{a_{22}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1 & 5\\ {1/5} & 1 \end{array}} \right]$ | (5) |
(1) 计算判断矩阵${\textbf{A}}$的每一行元素的乘积${M_i} = {\left[ {\begin{array}{*{20}{c}} 5 & {1/5} \end{array}} \right]^{\rm{T}}}$
(2) 计算${M_i}$的平方根${\overline w _i} = {\left[ {\begin{array}{*{20}{c}} {2.2361} & {0.4472} \end{array}} \right]^{\rm{T}}}$
(3) 对向量${\overline w _i} = [ {\begin{array}{*{20}{c}} {{{\overline w }_1}} & {{{\overline w }_2}} \end{array}} ]$作归一化或正规划处理,即${w_i} = {\overline w _i}/\sum\limits_{i = 1}^2 {{{\overline w }_i}} $
${w_i} = [\begin{array}{*{20}{c}} {{w_1}} & {{w_2}} \end{array}]$为一级指标权重,故压缩机整体评价安全性指标和经济性指标在机组评价中的权重因子为:${w_i} = [\begin{array}{*{20}{c}} {0.83} & {0.17} \end{array}]$。
经查表二阶$R_{\rm{I}}$为零,对于二阶判断矩阵显然符合逆矩阵条件,也符合判断矩阵一致性条件。
在考虑部件安全性及经济性指标计算权重时,由于评价对象为压缩机组的20 个部件,故建立的安全性、经济性判断矩阵${\textbf{C}}_1$、${\textbf{C}}_2$ 皆为20 阶矩阵,在计算其特征向量及权重时需借助数学计算软件Matlab 来完成。安全性指标20 阶矩阵Matlab 软件计算得各部件权重$w_{1i}$,如表 6 所示,该权重为部件以安全性为考评指标的相对重要性的排序,为一无因次量。
| 表6 机组各部件安全性指标权重值$w_{1i}$ Table 6 The safety index weights $w_{1i}$ of the unit components |
经计算20阶判断矩阵${\textbf{C}}_1$的最大特征值${\lambda _{\max }}=20.181$,一致性指标${C_{\rm{I}}}{_1}=\dfrac{{{\lambda_{\max }}-n}}{{n-1}}=0.0095$。查资料[7] 可得20阶判断矩阵${\textbf{C}}_1$的${R_{\rm{I}}}_1$为1.629~2,一致性比率${C_{\rm{R}}}{_1}= \dfrac{{{C_{\rm{I}}}{_1}}}{{{R_{\rm{I}}}{_1}}}=0.0058 <0.1$,符合单层次一致性要求。
考虑经济性指标建立的20 阶矩阵用Matlab 软件计算得各部件权重$w_{2i}$,如表 7 所示,该权重为部件以经济性为考评指标的权重大小,表明各部件相对重要性的排序,为一无量纲量。
| 表7 机组各部件经济性指标权重值$w_{2i}$ Table 7 The economic index weights $w_{2i}$ of the unit components |
同理可得:判断矩阵${\textbf{C}}_2$的最大特征值${\lambda _{\max }}=21.164~2$,一致性指标${C_{\rm{I}}}{_2}=\dfrac{{{\lambda_{\max}}-n}}{{n-1}}=0.061~3$,${R_{\rm{I}}}_2$为1.629~2,一致性比率${C_{\rm{R}}}{_2}=\dfrac{{C_{\rm{I}}}{_2}}{{R_{\rm{I}}}_2} =0.038 <0.1$,符合单层次一致性要求。
3.3 层次总排序及一致性检验 3.3.1 层次总排序天然气压缩机评价确定机组各部件权重的层次总排序为${w_i} = \sum\limits_{j = 1}^m {{w_j}{w_{ij}}} (i = 1, \cdots ,n)$ ,压缩机各部件在安全性指标与经济性指标下的综合权重为$w = {w_1}{w_{1i}} + {w_2}{w_{2i}}$,计算得各部件权重因子如表 8。
| 表8 天然气压缩机各部件权重值 Table 8 The weights of the natural gas compressor components |
总层次一致性$C_{\rm{R}}=\sum\limits_{i=1}^m {{w_i}{C_{\rm{I}}}{_i}}/\sum\limits_{i=1}^m {{w_i}{R_{\rm{I}}}{_i}}$检验,总层次一致性指标$C_{\rm{I}}=0.007~9$,总层次随机一致性指标$R_{\rm{I}}=1.629~2$,总层次一致性比率为$C_{\rm{R}} =\dfrac{{C_{\rm{I}}}}{{R_{\rm{I}}}}=0.004~9 <0.1$,故压缩机各部件权重总层次一致性比率具有较好的一致性,此层次分析法确定天然气压缩机各部件权重值时具有较合理的结果。
3.4 天然气压缩机各部件权重层次分析法计算得压缩机各部件权重为:曲轴为0.034,活塞杆4 个每个权重为0.017 5,连杆4 个每个权重为0.019 5,连接螺栓为0.021,机身为0.036,中体2 个每个权重为0.013 5,飞轮为0.020,缸体4 个每个权重为0.028 5,缸盖每个权重为0.011,活塞4 个每个为0.014 25,十字头4 个每个权重为0.017 75,余隙缸体4 个每个权重为0.021 75,轴承3 个每个权重为0.017,风扇1 组权重为0.021,空冷器权重为0.055,缓冲罐4 个每个权重为0.015,分离器2 个每个权重为0.013 5,工艺气管道权重为0.027,仪控系统权重为0.032,润滑系统权重为0.026。
4 结论(1)运用层次分析法(AHP)确定天然气压缩机安全评价中各部件权重系数,将具有模糊特征的安全性指标和具有确定性特征的经济性指标综合起来考虑,将复杂问题进行定性与定量分析,达到理想的一致性判断结果。
(2)用层次分析法确定天然气压缩机各部件权重系数得到稳定的计算结果,针对安全性指标和经济性指标的高阶判断矩阵用Matlab 软件计算判断矩阵特征向量、最大特征值及各部件权重,并经多次调整达到满意的一致性要求,以确保得到比较合理的权重系数。
(3)综合评价安全性和经济性指标得到权重系数较高的部件为空冷器0.055、机身0.036、曲轴0.034、仪控系统0.032,各部件权重符合机组系统中部件自身重要性趋势要求,对权重较大部件在平时运行维修过程中应给予重点关注。
| [1] |
常建娥, 蒋太立. 层次分析法确定权重的研究[J].
武汉理工大学学报:信息与管理工程版, 2007, 29 (1) : 153 –156.
Chang Jian'e, Jiang Taili. Research on the weight of coefficient through analytic hierarchy process[J]. Journal of Wuhan University of Technology:Information & Management Engineering, 2007, 29 (1) : 153 –156. |
| [2] |
李海华, 赵洪泽, 李海强. 基于模糊层次分析法的煤矿工程评标指标权重的确定[J].
煤炭技术, 2013, 32 (2) : 54 –56.
Li Haihua, Zhao Hongze, Li Haiqiang. Based on fuzzy analytic hierarchy process in coal mine engineering bid evaluation index weight determination[J]. Coal Technology, 2013, 32 (2) : 54 –56. |
| [3] | Saaty T L. How to handle dependence with the analytic hierarchy process[J]. Mathematical Modelling, 1987, 9 (3-5) : 369 –376. DOI:10.1016/0270-0255(87)90494-5 |
| [4] | Saaty T L. A new macroeconomic forecasting and policy evaluation method using the analytic hierarchy process[J]. Mathematical Modelling, 1987, 9 (3-5) : 219 –231. DOI:10.1016/0270-0255(87)90479-9 |
| [5] |
高建, 何仁洋, 王德国. 用层次分析法评价跨越管桥的洪水风险[J].
天然气工业, 2010, 30 (2) : 106 –109.
Gao Jian, He Renyang, Wang Deguo. Flood risk assessment on pipeline bridge based on the analytic hierarchy process[J]. Natural Gas Industry, 2010, 30 (2) : 106 –109. |
| [6] |
刘刚, 金业权, 李峰, 等. 层次分析法在井控风险可控诱因分析中的应用[J].
西南石油大学学报:自然科学版, 2011, 33 (2) : 137 –141.
Liu Gang, Jin Yequan, Li Feng, et al. The application of ahp method in well control risk evaluation by controllable factor analysis[J]. Journal of Southwest Petroleum University:Science & Techonology Edition, 2011, 33 (2) : 137 –141. |
| [7] |
王惠明, 梁政. LNG汽车产业发展可行性的模糊分析[J].
西南石油大学学报:自然科学版, 2012, 34 (6) : 161 –168.
Wang Huiming, Liang Zheng. The fuzzy analysis of development feasibilities of the LNG vehicles industry[J]. Journal of Southwest Petroleum University:Science & Techonology Edition, 2012, 34 (6) : 161 –168. |
| [8] |
吴旭, 王旭本, 阚瑷珂, 等. 基于层次分析法的流域生态决策评价系统[J].
成都理工大学学报:自然科学版, 2011, 38 (2) : 126 –131.
Wu Xu, Wang Xuben, Kan Aike, et al. Watershed ecological assessment system of decision-making based on AHP method[J]. Journal of Chengdu University of Technology:Science & Technology Edition, 2011, 38 (2) : 126 –131. |
| [9] |
谢祥俊, 邱全峰, 鲁柳利. 油藏经营管理综合评价的层次分析方法[J].
西南石油大学学报:自然科学版, 2009, 31 (3) : 150 –153.
Xie Xiangjun, Qiu Quanfeng, Lu Liuli. AHP method of the synthetical evaluation model of reservoir management[J]. Journal of Southwest Petroleum University:Science & Techonology Edition, 2009, 31 (3) : 150 –153. |
| [10] |
童岱, 黄海波, 侯江波, 等. CNG汽车产业综合效益评价方法[J].
天然气工业, 2010, 30 (12) : 107 –109.
Tong Dai, Huang Haibo, Hou Jiangbo, et al. An evaluation method for the comprehensive benefits of CNG vehicle industry[J]. Natural Gas Industry, 2010, 30 (12) : 107 –109. |
| [11] |
李昆仑. 层次分析法在城市道路景观评价中的应用[J].
武汉大学学报:工学版, 2005, 38 (1) : 143 –147.
Li Kunlun. Using analytic hierarchy process in urban road landscape evaluation[J]. Engineering Journal of Wuhan University, 2005, 38 (1) : 143 –147. |
| [12] |
孟陆波, 李天斌, 龚勇. 基于模糊层次综合评判的大变形预测方法[J].
成都理工大学学报:自然科学版, 2010, 37 (2) : 195 –200.
Meng Lubo, Li Tianbin, Gong Yong. Large deformation forecasting method based on fuzzy hierarchical integrated evaluation[J]. Journal of Chengdu University of Technology:Science & Technology Edition, 2010, 37 (2) : 195 –200. |
| [13] |
危向峰, 段建南, 胡振琪, 等. 层次分析法在耕地地力评价因子权重确定中的应用[J].
湖南农业科学, 2006 (2) : 39 –42.
Wei Xiangfeng, Duan Jiannan, Hu Zhenqi, et al. Applying analytic hierarchy process to determining farmland productivity evaluation factors'weight[J]. Hunan Agricultural Sciences, 2006 (2) : 39 –42. |
| [14] |
熊锐, 曹锟生. 多目标决策的层次分析法[J].
系统工程理论与实践, 1992 (6) : 58 –62.
Xiong Rui, Cao Kunsheng. Hierarchical analysis of multiple criteria decision making[J]. Systems Engineeringtheory & Practice, 1992 (6) : 58 –62. |
| [15] |
路萍, 吴斌. 层次分析法在高等院校科技评价系统中的应用[J].
北京工业大学学报, 2002, 28 (3) : 358 –362.
Lu Ping, Wu Bin. Application of AHP in the Sci & Tech assessment system of colleges and universities[J]. Journal of Beijing Polytechnic University, 2002, 28 (3) : 358 –362. |
| [16] |
康毅力, 王海涛, 游利军, 等. 基于层次分析法的地层钻井液漏失概率判定[J].
西南石油大学学报:自然科学版, 2013, 35 (4) : 180 –186.
Kang Yili, Wang Haitao, You Lijun, et al. Probability determination for loss circulation of drilling fluids based on analytic hierarchy process[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2013, 35 (4) : 180 –186. |
| [17] |
曾建权. 层次分析法在确定企业家评价指标权重中的应用[J].
南京理工大学学报, 2004, 28 (1) : 99 –104.
Zeng Jianquan. Application of analytic hierarchy process to determining entrepreneur evaluation idex weight[J]. Journal of Nanjing University of Science and Technology, 2004, 28 (1) : 99 –104. |
| [18] |
王其冬, 武佩珍, 程建刚, 等. 层次分析法在国家自然科学基金项目评审中的应用[J].
系统工程理论与实践, 2001 (7) : 119 –123.
Wang Qidong, Wu Peizhen, Cheng Jiangang, et al. Application of AHP method in evaluating projects of national natural science fund[J]. Systems Engineering-theory &Practice, 2001 (7) : 119 –123. |
| [19] |
洪志国, 李焱, 范植华, 等. 层次分析法中高阶平均随机一致性指标(RI)的计算[J].
计算机工程与应用, 2002 (12) : 45 –47.
Hong Zhiguo, Li Yan, Fan Zhihua, et al. Caculation on high-ranked RI of analytic hierarchy process[J]. Computer Engineering and Applications, 2002 (12) : 45 –47. |
| [20] |
朱建军, 王梦光, 刘士新. AHP判断矩阵一致性改进的若干问题研究[J].
系统工程理论与实践, 2007 (1) : 18 –22.
Zhu Jianjun, Wang Mengguang, Liu Shixin. Research on consistency modification problem of comparison matrix in the analytical hierarchy process[J]. Systems Engineeringtheory & Practice, 2007 (1) : 18 –22. |
| [21] | Kwiesielewicz M, Uden E. Inconsistent and contradictory judgments in pairwise comparison method in the AHP[J]. Computers & Operations Research, 2004, 31 (5) : 713 –749. |
| [22] |
房向荣, 周宏安. 部分权重信息下对方案有偏好的不确定多属性决策法[J].
西安石油大学学报:自然科学版, 2011, 26 (1) : 99 –102.
Fang Xiangrong, Zhou Hongan. Approach of uncertain multi attribute decision-making with preference information of alternatives under partial weight information[J]. Journal of Xi'an Shiyou University:Natural Science Edition, 2011, 26 (1) : 99 –102. |
| [23] | Belton V. A comparison of the analytic hierarchy process and a simple multi-attribute value function[J]. European J.Oper. Res, 1986, 26 (1) : 7 –21. DOI:10.1016/0377-2217(86)90155-4 |
| [24] |
李丁, 韩伟一, 汪云林. 关于层次分析法的数值试验[J].
统计与信息论坛, 2013, 28 (2) : 10 –13.
Li Ding, Han Weiyi, Wang Yunlin. Numerical experiment on the analytic hierarchy process[J]. Statistics & Information Forum, 2013, 28 (2) : 10 –13. |
 2014, Vol. 26
2014, Vol. 26

