石油是工业和人类社会发展的重要资源和战略物资。有杆抽油系统的井下泵组在近千米到数千米的井下工作,工况极其恶劣,有杆抽油设备发生故障的概率较高。一旦发生了故障,不及时诊断出来,就会影响生产,给企业、国家造成损失。有杆抽油系统故障诊断的方法主要包括:五指式动力仪分析方法、地面示功图分析法[1]、井下功图诊断法、有杆抽油系统力学模型分析方法[2-8] 和人工智能故障诊断方法[9-19] 等。
目前有杆抽油系统的故障诊断主要是先通过有杆抽油系统力学模型分析示功图来得到泵功图,再以正常样本和尽可能多类型故障样本的泵功图作为训练集,训练出相应模型后再对各样本进行故障诊断。2005 年周继德根据大庆油田的实例分析了抽油机井的泵况判断方法,并进行故障处理。2008 年胡广杰等分析了塔河油田深井泵发生不同故障时示功图不同的规律性特征,再结合诊断分析的要素和油井实际情况,对油井泵况做出判断。上述工作对有杆抽油系统故障机理及发生不同故障时示功图不同的规律性特征进行了很好的总结,但采用的仍是人工诊断方法,效率低,人工工作量大。2007 年XuPeng[9] 等应用216 个输入和5 个输出自组织竞争神经网络,选取5 种不同工作状态的示功图(供液不足、下碰泵、正常、气体影响和结蜡)共1 550 个训练样本,6 337 个测试样本,训练100 次识别正确识别率为99.92%。2009 年张强[10] 等选取6 种不同工作状态的示功图(正常、出砂、游动凡尔漏失、上碰泵、结蜡油稠、游动凡尔和固定凡尔都漏失)共136 个样本,96 个训练样本,40 个测试样本,训练1 560 次后,正确识别率为87.50%。2009 年De Lima[11] 等应用傅立叶描述子和皮尔逊相关方法对示功图进行故障识别,选取102 个样本,6 种工作状态,正确识别率为89%。有杆抽油系统是一个机电液耦合的复杂非线性系统,边界条件和阻尼系数很难准确确定,导致该系统力学模型的建立和求解非常困难;并且,油井功图样本量大、平稳状态多、类别不均衡,使训练集中缺少很多类型的故障样本,尤其是严重故障的样本。由于有杆抽油系统的复杂性,至今都没有一个完全有效的手段来对抽油机井井下故障进行实时、准确的故障诊断。
地面示功图是抽油井采油现场采集的第一手资料,基于地面示功图来实现有杆抽油系统的实时诊断和监控对解除油井故障、保证油井正常生产或提高油井产量等就显得非常重要而且具有现实意义。
1 有杆抽油系统故障递阶诊断方法每组示功图数据包括载荷和位移,共216 对数据。油田一个小时采集一次示功图,一天就有24组数据,一个星期有168 组数据,一个月(30 d 计算)有720 组数据。所以,油井示功图数据多、样本量大。并且,对于油田来讲,绝大多数都是平稳的工作状态,包括两种情况:一是油井正常,大部分示功图均正常,故障样本和故障类型较少;二是有的油井以某种故障,如含气、出砂、供液不足、轻微碰挂、振动影响等某类对生产影响不太大的故障为主,出现其他故障的概率较低。以上两种情况不需要立即停产进行检修,可以待下次修井时或在方便和必要时处理,也就是说大量的油井示功图数据都是不需要立即进行故障处理的。而一旦出现凡尔失灵、抽油杆断脱、泵卡死等严重故障,均需立即停产,及时采取检泵和修井措施,以减少损失。油井修井措施,特别是对油井大修或更换设备会对油井的生产状况和功图产生影响,检修前后的生产状况和功图往往会有较大差别,检修后的训练集和样本特征往往需要重新形成。另外,现有的采油工业中抽油机数量大、分布广,这更增加了井下状况的复杂性,使各口井均有自身特点,可能出现的故障类型也不固定。
针对有杆抽油系统特性和油井示功图样本量大、平稳状态多、类别不均衡(尤其缺少严重故障的样本)的特点,以正常(或平稳状态)样本示功图作为切入点,提出了基于示功图的有杆抽油系统故障递阶诊断方法,即:首先在故障分辨阶段根据正常(或平稳状态)样本的统计规律把示功图分为故障类和非故障类;然后从故障机理入手,将统计理论与搜索树结合在一起,针对故障样本进行详细的故障识别。其流程图如图 1。
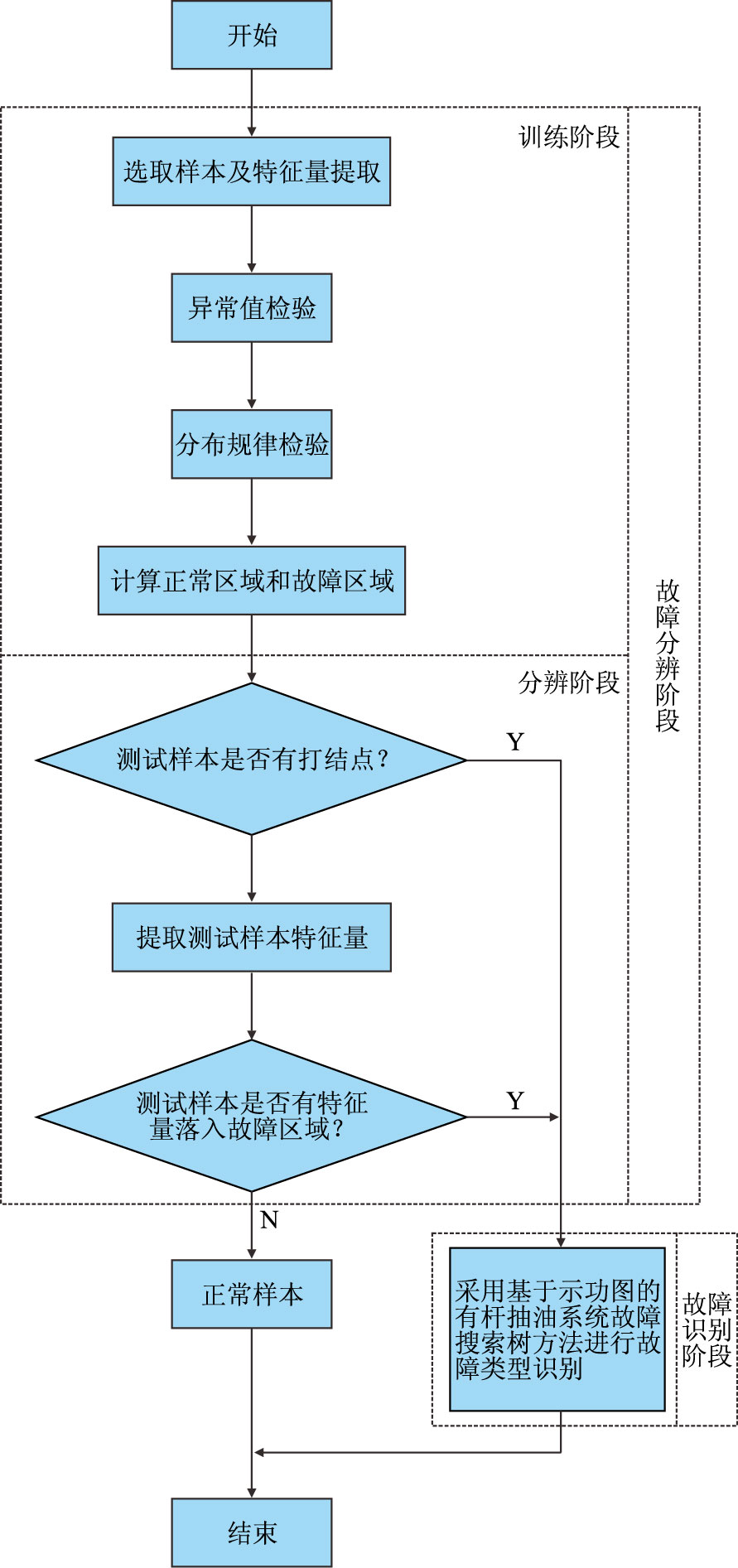 |
| 图1 基于示功图的有杆抽油系统故障递阶诊断法流程图 Fig. 1 Fault hierarchical diagnosis flowchart of rod pumping system based on dynamometer |
基于示功图的有杆抽油系统故障递阶诊断方法在保持计算简单的前提下,提高了分类的精度,尤其是针对小样本异常事件,从而提高了故障诊断系统的故障诊断性能;它不需要建立和求解有杆抽油系统力学模型,也不存在训练集问题;先进行故障分辨可节省大量时间,提高油田管理的效率;另外,故障分辨的训练样本来自于正常(或平稳状态)样本,样本丰富且能反映出有杆抽油系统自身的基本特征。
本文将首先对有杆抽油系统故障递阶诊断的故障分辨进行研究。
2 故障分辨故障分辨主要分为两个阶段:
(1)训练阶段:在训练阶段由正常(或平稳)样本提取特征量,根据这些样本的特征量得到相关统计信息;
(2)分辨阶段:根据在训练阶段得到的统计信息,进行故障分辨,根据测试样本是否有特征量落入故障区域来判断其分类。
2.1 训练阶段训练过程如下:首先,人工选取n个正常样本,进行除打结点外的15个特征量(包括下死点(E点)载荷、 上死点(F点)位移和载荷、固定凡尔打开点(B点)的位移和载荷、游动凡尔打开点(D点)的位移和载荷、 面积、最大载荷、最小载荷、载荷总的平均变化量,$EB$、$BF$、$FD$、$DE$段载荷的平均变化量)的提取(图 2)[13];其次,对特征量进行异常值检验,如果异常,则由人工再进行判断是否是异常值,若确定为异常值,则剔除该样本,并重新进行异常值检验,直至没有异常值;然后,对这些检验后的高质量的样本进行分布规律统计;最后,根据统计结果计算正常区域和故障区域。
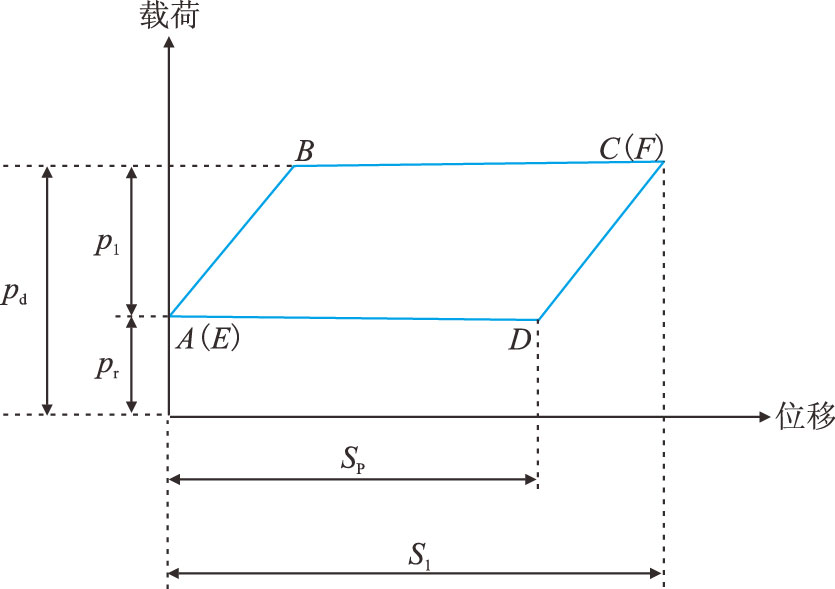 |
| 图2 弹性静载理论示功图 Fig. 2 Elastic static load theoretical surface dynamometer card |
由于“噪音”的存在会造成异常的观测结果或数据,称这种数据为异常值。
“噪音”的来源有多种多样,对于示功图位移和载荷的观测值来说,大致可以分为以下两类:(1)在复杂的实际工作过程中,由于各种异常因素的干扰引起的“异常误差”;(2)不可控制及未加控制的各种自变量、所用的仪器仪表在检测和传感的过程中引入的干扰和偏差、技术人员自身在处理和观察过程中的误操作以及观测条件的限制对观测数据的准确性产生的较大影响。
本文先利用数字计算机采用t检验准则指出可疑异常值,然后再由人工对可疑异常值进行技术判断,即结合技术判别法和统计判别法两种方法对训练样本进行检查、判别。
2.1.2 特征量分布规律检验在本文研究情况下,数据属于哪一种类型的分布是未知的,因此要对分布进行假设,并检验其与实际分布是否相符合。首先,选取6 个常用的连续性随机分布[14]:指数分布、均匀分布、威布尔分布、正态分布、瑞利分布和伽马分布为备选的分布类型,对样本数据分布进行假设;然后,采用${\chi^2}$ 拟合优度检验法检验假设分布与实际分布是否相符合,并在检验的过程中采用相同的置信度($\alpha$=0.05)。
${\chi^2}$拟合优度检验法是最主要的一种非参数检验方法,它实质上是要解决可否用已知总体的分布去拟合未知总体X的分布,其思想是将样本空间划分成k个互不相交的区间$\left({{a_0},{a_1}} \right]$,$\left({{a_1},{a_2}} \right]$,$\cdots\cdots$,$\left({{a_{k-1}},{a_k}} \right]$,$n_i$为落入第i个子区间中的实际频数,$n = \sum\limits_{i = 1}^k {{n_i}}$为样本容量。然后从考察实际频数$n_i$与期望频数$np_i$的差异的显著性入手,寻求并构造下列服从 ${\chi^2}$分布的检验统计量
| ${\chi ^2} = \sum\limits_{i = 1}^k {\dfrac{{{{{\rm{(}}{n_{\rm{i}}} - n{p_i})}^2}}}{{n{p_i}}}} $ | (1) |
英国著名统计学家皮尔逊证明了当样本容量n很大的时候,这个统计量近似地服从${\chi^2}(k-1)$分布。统计学家费歇又证明了当分布函数中含有r个未知参数,需要以它们的极大似然估计去替代时,这个统计量近似地服从${\chi^2}(k-1-r)$分布。于是对于给定的显著性水平$\alpha$,确定检验的拒绝域为$\left( {{\chi _{1 - \alpha }}^2\left( {k - r - 1} \right), + \infty } \right)$。最后,根据样本计算的统计量是否落入拒绝域来判断原假设是否成立。
有的样本数据服从两种或两种以上的分布类型,遇到这种情况,本文根据检验结果分别求取正常区域后取并集。
2.1.3 计算正常区域和故障区域首先,可以根据特征量的重要性、特征量统计的离散性、样本的可靠性、样本容量、抽样方式等因素确定该特征量正常区域的概率[14-15]。如图 3 所示,区间[b; a] 表示正常区域,样本落入该区间的概率为特征量正常区域的概率$\alpha$。
 |
| 图3 正常区域和故障区域概率示意图 Fig. 3 Schematic diagram of normal and fault zone |
本文经过综合考虑,对各特征量选取统一的。并假定故障区域1 和故障区域2 的概率相同,且同一特征量的正常区域概率与故障区域概率之和满足归一条件,则
| $P\{ - \infty < X < b\} + P\{ b \leqslant X \leqslant a\} \\ + P\{ a < X < + \infty \} = 1 \\P\{ - \infty < X < b\} = P\{ a < X < + \infty \} $ | (2) |
| $P\{ - \infty < X < b\} = P\{ a < X < + \infty \} $ | (3) |
| $P\{ - \infty < X < b\} = P\{ a < X < + \infty \} \\ {\rm{ }} = \dfrac{{1 - P\{ b \leqslant X \leqslant a\} }}{2} = \dfrac{{1 - \alpha }}{2} \\$ | (4) |
所以
| $P\{ - \infty < X < a\} = \alpha + \dfrac{{1 - \alpha }}{2} = \dfrac{{1 + \alpha }}{2}$ | (5) |
根据式(4)、式(5)及该特征量的分布类型与参数,可计算出a、b,即可得到正常区域区间$[b,a]$与故障区域区间$(-\infty,b)\cup(a,+\infty)$。对于载荷平均变化量,有意义的故障区域为$(a,+\infty)$。
例如某特征量服从正态分布,根据式(4)和式(5),$\alpha$=99.9%,可得$b=\mu-3.2905\sigma$,$a=\mu+3.2905\sigma$($\mu$—均值,$\sigma$—均方差),则该特征量的正常区域区间$[\mu-3.2905\sigma,\mu+3.2905\sigma]$,故障区域区间$(-\infty,\mu-3.2905\sigma)\cup (\mu+3.2905\sigma,+\infty)$。
如果对某特征量的假设检验不能确定它的分布规律,最好的方法是增加样本的数量n。另外,我们可以利用切比雪夫(Chebyshev)不等式[14] 来确定正常区域区间$[b,a]$。
2.2 分辨阶段下碰泵、二级振动等存在打结点的故障是根据测试样本本身是否存在打结点来分辨,而其他故障是根据测试样本的某个特征量落入故障区域即可判断其为故障样本。故障分辨具体流程见图 1。
3 算例以江苏油田李堡14 井5 个月的数据为实例。李堡14 井故障分辨的基本过程:提取一月份正常样本的特征值,找出分布规律,得到正常区域,对本月和二月份的的示功图进行故障分辨,以次类推,用前一个月的样本特征对本月和下个月的示功图进行故障分辨。一月份半个月数据(剔除异常数据和故障样本)作为训练样本得到假设检验结果,结果表明:所有样本都符合均匀分布,其中B点和F点位移还符合正态分布、韦伯分布、伽马分布,$EB$和$FD$载荷平均变化量还符合韦伯分布、指数分布、瑞利分布、伽马分布。
各特征量正常区域的概率均选取为99.99%,根据特征量对应的某种分布及参数,可计算该特征量在该分布下的正常区域,另外,考虑样本的随机性,由样本的最大值、最小值往外扩大20% 得到一个区域,区域的并集即为该特征量的正常区域。以此类推,分别计算15 个特征量的正常区域如下:
E 点载荷:[56.556,62.114]
B 点位移:[0.131,0.474]
B 点载荷:[69.254,74.476]
F 点位移:[1.542,2.165]
F 点载荷:[64.366,71.814]
D 点位移:[1.429,1.822]
D 点载荷:[52.122,57.358]
面积:[18.260,29.166]
最大载荷:[69.314,74.466]
最小载荷:[52.160,57.130]
总载荷平均变化量:[0.165,0.268]
EB 载荷平均变化量:[0.325,0.542]
BF 载荷平均变化量:[0.013,0.278]
FD 载荷平均变化量:[0.252,0.578]
DE 载荷平均变化量:[0.055,0.181]
进入到分辨阶段,运行故障分辨程序,分别对一月份和二月份的示功图数据进行故障分辨。一月份共744 个样本,29 个故障,结果故障分辨正确率100%。二月份共672 个样本,1 个故障,结果故障分辨正确率100%。一月份分辨出来的29 个故障样本示功图类似,且样本号连续,为497~526,其中523作为异常数据已经剔除,样本526 的示功图见图 4。
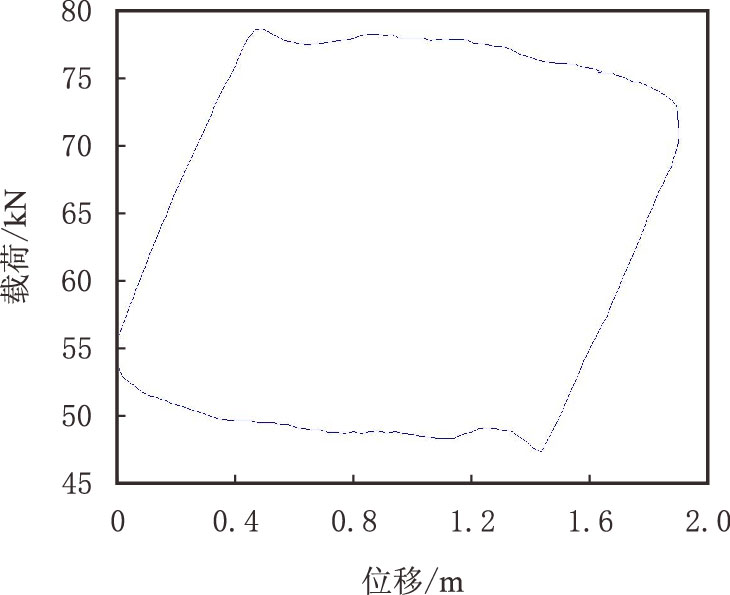 |
| 图4 样本526 的示功图 Fig. 4 Dynamometer of sample 526 |
经过人工判断,样本497~526均是油稠故障。故障分辨结果分别提示为E点载荷过小(包括样本516,517,524~526)、B点位移过小(包括样本521)、B点载荷过大(包括样本497~515,518~520,522)。二月份分辨出来的1个故障,样本1 065示功图见图图 5,故障分辨结果提示为打结,打结点位移0.005。
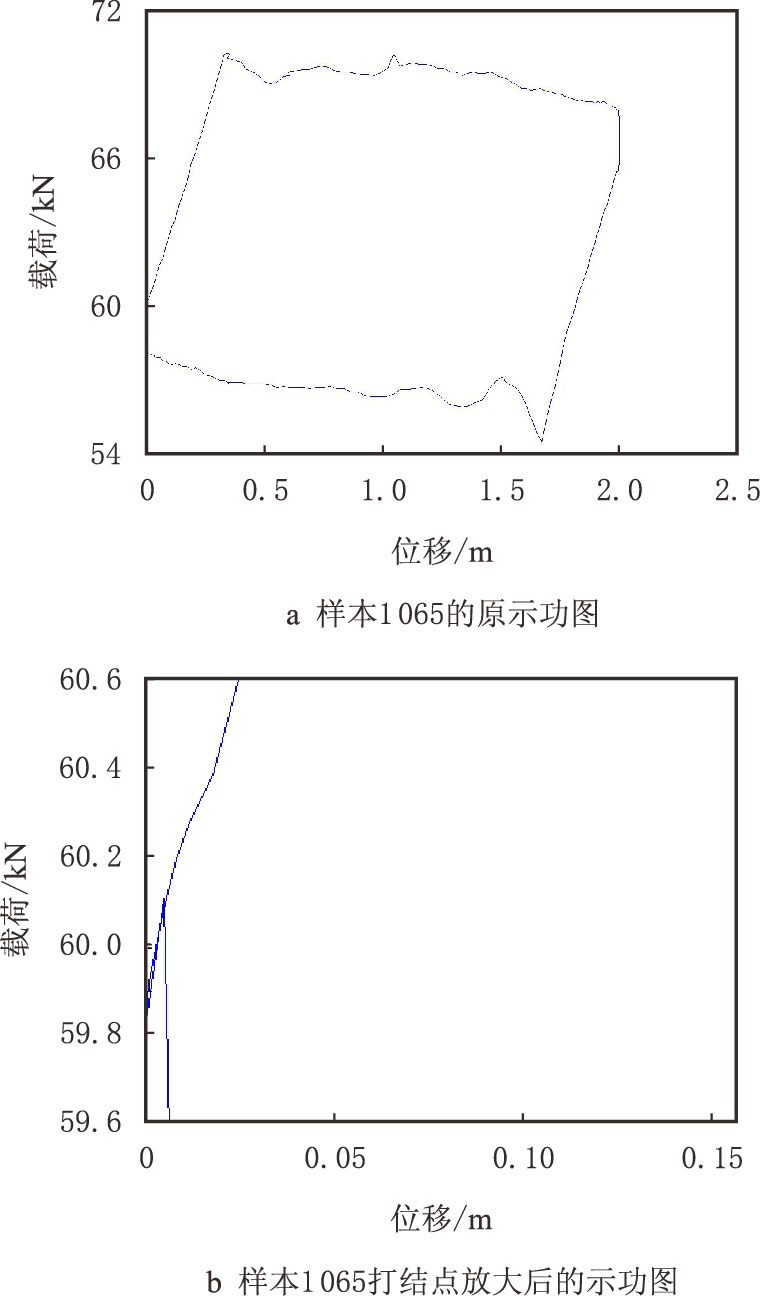 |
| 图5 样本1 065 的示功图 Fig. 5 Dynamometer of sample 1065 |
对李堡14 井5 个月的数据进行故障分辨,结果汇总见表 1。
| 表1 故障分辨结果汇总 Table 1 Data summary of failure distinguishing |
由表 1 可以看出:
(1)故障分辨过程节省时间,从大量的数据中筛选出故障样本,分辨的正确率比较高,分辨的正确率平均为99.28%。
(2)所有的故障样本基本全部分辨出来,分辨错误的主要表现在将正常样本判断为故障。
(3)训练样本的假设检验结果显示,每个月的每个特征量均符合均匀分布,说明李堡14 井生产状况比较平稳;正是由于该井生产状况平稳,因而各特征量波动小,稍有波动的正常样本会被分辨为故障。
(4)对于生产状况平稳的井,正常区域的概率取得较大,分辨效果较好。
(5) 李堡14 井的故障主要出现在两个阶段:第一月的样本497~526 和第四个月的样本2 564~2 574,第一月的样本497~526 均是油稠故障,第四个月的样本2 564~2 574 主要是供液不足故障,分辨结果较好地反映了李堡14 井局部时间内的井下状况。
(6)对于筛选出的故障样本,其故障分辨结果提示仅能反应其故障的某一个方面信息(主要是异常信息),故障分辨过程并不能也不需要将故障样本的所有信息都反映出来。
4 结论(1)有杆抽油系统工况极其恶劣,发生故障的概率较高。针对有杆抽油系统特性和油井示功图样本量大、平稳状态多、类别不均衡(尤其缺少严重故障的样本)的特点,以正常(或平稳状态)样本示功图作为切入点,提出了基于示功图的有杆抽油系统故障递阶诊断方法,即:首先在故障分辨阶段根据正常(或平稳状态)样本的统计规律把示功图分为故障类和非故障类;然后从故障机理入手,将统计理论与搜索树结合在一起,针对故障样本进行详细的故障识别。
(2)基于示功图的有杆抽油系统故障递阶诊断方法在保持计算简单的前提下,提高了分类的精度;它不需要建立和求解有杆抽油系统力学模型,也不存在训练集问题;先进行故障分辨可节省大量时间,提高油田管理的效率;另外,故障分辨的训练样本来自于正常(或平稳状态)样本,样本丰富且能反映出有杆抽油系统自身的基本特征。
(3)故障分辨包括训练和分辨两个阶段。在训练阶段,对选取的样本的特征量采用t检验准则剔除异常数据后,对正常(或平稳状态)样本的分布规律进行${\chi^2}$拟合优度检验,从而确定正常(或平稳状态)样本的随机分布形式及其参数;然后,根据假设检验结果计算出正常区域和故障区域。在分辨阶段,根据测试样本是否有特征量落入故障区域来判断其分类。
(4)对江苏油田李堡14 井5 个月的实测数据进行了故障分辨研究,结果表明故障分辨过程能从大量的数据中筛选出故障样本,分辨的正确率比较高;分辨结果能较好地反映了油井局部时间内的井下状况;训练样本的统计规律能反映油井实时的生产状况。
| [1] | Abello J, Houang A, Russell J. A hierarchy of pattern recognition algorithms for the diagnosis of sucker rod pumped wells[C]. 5th International Conference on Computing and Information, 1993:359-364. |
| [2] | Gibbs S G, Neely A B. Computer diagnosis of down-hole conditions in sucker rod pumping wells[C]. SPE 1165, 1965. |
| [3] | 张宏, 刘海浪, 孙应民. 定向井有杆泵抽油系统的有限元分析[J]. 石油学报, 2000, 21 (6) : 102 –106. |
| [4] |
刘清友, 何玉发. 有杆抽油系统诊断方法研究与应用[J].
西南石油大学学报:自然科学版, 2008, 30 (1) : 1 –4.
Liu Qingyou, He Yufa. Study of the method to diagnose sucker rod pumping system and its application[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2008, 30 (1) : 1 –4. |
| [5] |
彭勇, 余国安. 识别泵工况的分类器设计[J].
西安石油学院学报, 1995, 10 (3) : 35 –37.
Peng Yong, Yu Guo'an. Design of the separator used to recognize the working condition of the sucker rod pump in a pumping well[J]. Journal of Xi'an Petroleum Insistute, 1995, 10 (3) : 35 –37. |
| [6] | Cerqueira J F, Correa J F, Bittencourt A C. Development of an intelligent distributed management system for automated wells[J]. SPE 77609, 2002 . |
| [7] | Zhang Shirong, Tang Yuling. Indirect measurement of dynamometer card of pumping unit[C]. The 7th World Congress on Intelligent Control and Automation, 2008:4952-4955. |
| [8] | Rowlan O L,Lea J F,Mccoy J N. Overview of beam pump operations[C]. SPE 110234, 2007. |
| [9] | Xu Peng, Xu Shijin, Yin Hongwei. Application of selforganizing competitive neural network in fault diagnosis of sucker rod pumping system[J]. Journal of Petroleum Science and Engineering, 2007, 58 (1-2) : 43 –48. DOI:10.1016/j.petrol.2006.11.008 |
| [10] |
张强, 许少华. 智能动态诊断模型及在示功图识别中的应用[J].
计算机工程与应用, 2009, 45 (4) : 215 –217.
Zhang Qiang, Xu Shaohua. Interlligent dynamic diagnosis method and its application in identification of indicator diagram[J]. Computer Engineering and Applications, 2009, 45 (4) : 215 –217. |
| [11] | De Lima, Guedes, Sliva. Application of fourier descriptors and pearson correlation for fault detection in sucker rod pumping system[C]. IEEE Conference on Emerging Technologies and Factory Automatio, 2009:1-4. |
| [12] | Liang Hua, Li Xunming. Accurate extraction of valve opening and closing points based on the physical meaning of surface dynamometercard[J]. Petroleum Exploration and Development, 2011, 38 (1) : 109 –115. DOI:10.1016/S1876-3804(11)60018-9 |
| [13] | 陈魁. 应用概率统计[M]. 北京: 清华大学出版社, 2000 . |
| [14] |
张玉斌, 齐卫红. 有杆泵抽油系统可靠性数字仿真研究[J].
系统仿真学报, 2003, 15 (2) : 242 –246.
Zhang Yubin, Qi Weihong. Research on the reliability digital simulation of rod pumping system[J]. Journal of System Simulation, 2003, 15 (2) : 242 –246. |
| [15] | Scott W L, Elton J S, Albert S G. Total downstroke friction from downhole dynamometer analysis[C]. SPE 67274, 2001. |
| [16] | Mccoy J N, Jennings J W, Capps K S, et al. Simplified computer-aided analysis of electrical current in motors used for beam pumping systems[C]. SPE 25447, 1993. |
| [17] | Doty D R. Performance of electric submersible pumps in gassy wells[C]. SPE 22767, 1994. |
| [18] | Cerqueira J F, Correa J F, Bittencourt A C. Development of an intelligent distributed management system for automated wells[C]. SPE 77609, 2002. |
| [19] | Li Hongsheng, Wang Yu, Ding Yongzhong, et al. Implemention of network-computing and NN based remote real-time oil well monitoring system[C]. 2005 International Conference on Neural Networks and Brain, 2005. |
 2014, Vol. 26
2014, Vol. 26

