2. 中国石油新疆油田分公司勘探开发研究院, 新疆 克拉玛依 834000;
3. 中国石油西南油气田分公司川中油气矿, 四川 遂宁 629000
2. Research Institute of Exploration and Development, Xinjiang Oilfield Company, CNPC, Karamay, Xinjiang 834000, China;
3. Middle Sichuan Gas Fields of Southwest Oil and Gasfield Company, CNPC, Suining, Sichuan 629000, China
泡沫排液采气是气井最经济有效的排液采气方式之一[1],深入研究其排液过程中的井筒多相流流型及压降规律是对该工艺进行优化设计的基础。李兆敏、李松岩、王冠华等曾建立了井筒中均质稳定的泡沫流体的水力学模型[2-4]。然而在泡排过程中井筒流型并非总是呈现均质稳定的泡沫流,流体并非总是表现出幂律流体特征,当气井产气降低或产液增加时,体积含气率可能超出形成稳定泡沫所需要的范围,致使流型出现非泡沫流。因此不能忽略泡排井流型的多变性。
经验模型受测试条件限制通常只适用于特定的流动条件或流型条件[5],因此难以适应泡排井流型的多变性。而机理模型是基于基本物理原理所建立的,适用于更宽的流型范围,更具通用性[6]。本文引入机理模型的构思,以Mitchell B J 和Taitel Y 等[7-8]的流型实验为基础,从物理机理的角度建立了泡排井的流型转换界限,并针对各流型建立了相应的压降计算模型。
1 流型转换界限泡沫排液采气井的产出流体来自气井自生气、液,因此其体积含气率具有宽的分布范围。根据Mitchell B J 等的实验研究[7],体积含气率(即泡沫质量)在0.52∼0.96 时形成均质稳定的泡沫,当体积含气率大于0.96 时呈现雾状流,而体积含气率小于0.52 时呈现牛顿流体特征。又根据Taitel Y 等的流型实验[8],牛顿流体在体积含气率低于0.52 时的流型可能存在泡状流和段塞流。因此根据流型形成机理的不同可将泡排井的流型分为泡状流、段塞流、均质泡沫流和雾状流。
1.1 均质泡沫流的形成界限体积含气率在0.52∼0.96 时会形成均质稳定的泡沫,此时
| $0.52 < {Q_{\rm{g}}}/{Q_{\rm{m}}} = {v_{{\rm{sg}}}}/{v_{\rm{m}}} \leqslant 0.96$ | (1) |
式中:${Q_{\rm{g}}}$,${Q_{\rm{m}}}$—气相,混合物体积流量,m3/s;${v_{{\rm{sg}}}}$—气相表观流速,m/s;${v_{\rm{m}}}$—混合物流速,m/s。
考虑到混合物流速${v_{\rm{m}}} = {v_{{\rm{sg}}}} + {v_{{\rm{sl}}}}$,于是将均质泡沫流的形成界限表示为可测量的参数形式
| $ %{v_{{\rm{sg}}}} > 1.08{v_{{\rm{sl}}}} \hspace{0.5em}{或}\hspace{0.5em} {v_{{\rm{sg}}}} \leqslant 24{v_{{\rm{sl}}}} 1.08{v_{{\rm{sl}}}} < {v_{{\rm{sg}}}} \leqslant 24{v_{{\rm{sl}}}}$ | (2) |
式中:${v_{{\rm{sl}}}}$—液相表观流速,m/s。
1.2 雾状流的形成界限若气流速度较高,体积含气率大于0.96 时,不会出现稳定泡沫,而会形成雾状流,此时液相呈雾状分散于气相中,采用气、液表观流速表示该界限为
| ${v_{{\rm{sg}}}} > 24{v_{{\rm{sl}}}}$ | (3) |
若气流速度较低,体积含气率低于0.52 时同样无法保持稳定泡沫流,而是呈现牛顿流体性质,出现泡状流和段塞流。Taitel Y 等[8] 实验表明泡状流向段塞流转换的临界持气率${\alpha _{{\rm{max}}}}=0.25$,持气率高于0.25 时小气泡会聚合形成泰勒泡,从而形成段塞流。将其表示为漂移速度的形式
| $\dfrac{{{v_{{\rm{sg}}}}}}{{{\alpha _{{\rm{max}}}}}} = 1.2\left( {{v_{{\rm{sg}}}} + {v_{{\rm{sl}}}}} \right) + {v_\infty }$ | (4) |
式中:${v_\infty }$—气泡漂移速度,m/s。
气泡漂移速度${v_\infty }$ 可采用Harmathy 关系式[9]
| ${v_\infty } = 1.53{\left[ {\dfrac{{{\rm{g}}{\sigma _{\rm{l}}}\left( {{\rho _{\rm{l}}} - {\rho _{\rm{g}}}} \right)}}{{\rho _{\rm{l}}^2}}} \right]^{1/4}}$ | (5) |
式中:g—重力加速度,g=9.8 m/s2;${\sigma _{\rm{l}}}$—气液间表面张力,N/m;${{\rho _{\rm{g}}},{\rho _{\rm{l}}}}$—气相,液相密度,kg/m3。
泡状流的形成界限为
| ${v_{{\rm{sg}}}} \leqslant 0.357{v_\infty } + 0.429{v_{{\rm{sl}}}}$ | (6) |
段塞流的形成界限为
| $%{v_{{\rm{sg}}}} > 0.357{v_\infty } + 0.429{v_{{\rm{sl}}}} \hspace{0.5em}{且}\hspace{0.5em} {v_{\rm{sg}}} \leqslant 1.08{v_{\rm{sl}}} 0.357{v_\infty } + 0.429{v_{{\rm{sl}}}} < {v_{\rm{sg}}} \leqslant 1.08{v_{\rm{sl}}}$ | (7) |
另外在高液流速下,紊流作用可能导致大气泡破碎成小气泡,出现分散泡状流,其界限方程为
| ${\left[ {\dfrac{{0.4{\sigma _{\rm{l}}}}}{{\left( {{\rho _{\rm{l}}} - {\rho _{\rm{g}}}} \right){\rm{g}}}}} \right]^{0.5}}{\left( {\dfrac{{{\rho _{\rm{l}}}}}{{{\sigma _{\rm{l}}}}}} \right)^{0.6}}{\left( {\dfrac{f}{{2D}}} \right)^{0.4}}{\left( {{v_{{\rm{sg}}}} + {v_{{\rm{sl}}}}} \right)^{1.2}} \\{\hspace{2em}} = 0.725 + 4.15{\left( {\dfrac{{{v_{{\rm{sg}}}}}}{{{v_{{\rm{sg}}}} + {v_{{\rm{sl}}}}}}} \right)^{0.5}}$ | (8) |
式中:f—无滑脱摩阻系数(可由无滑脱雷诺数根据Moody图版查得),无因次;D—油管内径,m。
2 压降模型建立基于质量和动量守恒原理,油管多相流的总压力梯度方程可表示为重力压降、摩阻压降和加速度压降之和[6]。由于加速度项对总压降的影响通常很小,可将总压力梯度简化为
| $\dfrac{{{\rm{d}}p}}{{{\rm{d}}L}} = - {\rho _{\rm{m}}}{\rm{g}}\sin \theta - \dfrac{{{f_{\rm{m}}}{\rho _{\rm{m}}}v_{\rm{m}}^2}}{{2D}}$ | (9) |
式中:${\rho _{\rm{m}}}$—混合物密度,kg/m3;$f_{\rm{m}}$—Moody摩阻系数,无因次;$\theta$—油管与水平面的夹角,(°);L—长度,m;p—压力,Pa。
混合物密度是关于持气率$\alpha$ 的函数
| ${\rho _{\rm{m}}} = {\rho _{\rm{g}}}\alpha + {\rho _{\rm{l}}}\left( {1 - \alpha } \right)$ | (10) |
式中:${\alpha}$—持气率,无因次。
求解压力梯度方程的关键是确定持气率${\alpha}$ 和摩阻系数fm。
2.1 泡状流泡状流中小气泡分散在连续液相中,其上升速度沿截面分布不均,气液间存在滑脱,可采用漂移模型计算持气率[10]
| $\alpha = \dfrac{{{v_{{\rm{sg}}}}}}{{1.2\left( {{v_{{\rm{sg}}}} + {v_{{\rm{sl}}}}} \right) + {v_{\rm{b}}}}}$ | (11) |
式中:${v_{\rm{b}}}$—气泡漂移速度,m/s。
考虑气泡群的影响,气泡漂移速度vb 采用Zuber& Hench 公式[11]
| ${v_{\rm{b}}} = 1.53{\left[ {\dfrac{{{\rm{g}}{\sigma _{\rm{l}}}\left( {{\rho _{\rm{l}}} - {\rho _{\rm{g}}}} \right)}}{{\rho _{\rm{l}}^2}}} \right]^{1/4}}{\left( {1 - \alpha } \right)^{0.5}}$ | (12) |
粗糙管摩阻系数可按Jain[12] 显式公式计算,其中雷诺数按连续液相计算
| ${{\mathop{Re}\nolimits} _{\rm{l}}} = {\rho _{\rm{l}}}{v_{\rm{l}}}D/{\mu _{\rm{l}}}$ | (13) |
式中:${v_{\rm{l}}}$—液相真实流速,${v_{\rm{l}}} ={v_{{\rm{sl}}}}/\left( {1 - \alpha } \right)$,m/s;${\mu _{\rm{l}}}$—液相黏度,Pa⋅s。
若流型判断为分散泡状流,则气液接近无滑脱流动,持气率采用体积含气率计算
| $ \alpha = {v_{{\rm{sg}}}}/\left( {{v_{{\rm{sg}}}} + {v_{{\rm{sl}}}}} \right)$ | (14) |
段塞流中泰勒泡和液体段塞呈活塞状交替上升,气液间仍存在一定滑脱,同样采用漂移模型计算持气率[13]
| $ \alpha = \dfrac{{{v_{{\rm{sg}}}}}}{{1.2\left( {{v_{{\rm{sg}}}} + {v_{{\rm{sl}}}}} \right) + {v_{{\rm{TB}}}}}}$ | (15) |
其中泰勒泡漂移速度可采用Davies 和Taylor公式计算[14]
| $ {v_{{\rm{TB}}}} = 0.35{\left[ {\dfrac{{{\rm{g}}\sigma_{\rm{l}}\left( {{\rho _{\rm{l}}} - {\rho _{\rm{g}}}} \right)}}{{{\rho _{\rm{l}}}}}} \right]^{1/2}}$ | (16) |
而摩阻系数fm 计算方法同泡状流。
2.3 均质泡沫流均质稳定泡沫可视为单相幂律流体处理,持气率可按式(14)计算,而泡沫流体雷诺数可表示为[3]
| $ {{\mathop{ Re}\nolimits} _{\rm{F}}} = \dfrac{{8{D^n}v_{\rm{m}}^{2 - n}{\rho _{\rm{m}}}}}{{K{{\left( {\dfrac{{6n + 2}}{n}} \right)}^n}}}$ | (17) |
式中:K—稠度系数,Pa$\cdots^n$;n—流性指数,无因次。
稠度系数K 和流性指数n 可由Lord 实验结果确定[3]。当${{\mathop{Re}\nolimits} _{\rm{F}}} > 2300$时,Moody 摩阻系数可按Govier 非牛顿流体粗糙管摩阻系数公式计算[15]
| $ \sqrt {\dfrac{1}{{{f_{\rm{m}}}}}} = 2.03\lg \left( {\dfrac{D}{{2\varepsilon }}} \right) + 3.0 - \dfrac{{1.33}}{n}$ | (18) |
式中:"—油管绝对粗糙度,m。
当${{\mathop{Re}\nolimits} _{\rm{F}}} \leqslant 2300$时, ${f_{\rm{m}}}$采用Metzner公式[16]
| $ {f_{\rm{m}}} = \dfrac{{64}}{{{{{\mathop{ Re}\nolimits} }_{\rm{F}}}}}$ | (19) |
雾状流气流速度通常较高,具有较强的携液能力,因此可采用无滑脱模型描述。持气率仍按式(14)计算,而摩阻系数fm 根据无滑脱雷诺数计算,无滑脱雷诺数计算公式
| $ {{\mathop{ Re}\nolimits} _{{\rm{ns}}}} = \dfrac{{{\rho _{{\rm{ns}}}}{v_{\rm{m}}}D}}{{{\mu _{{\rm{ns}}}}}}$ | (20) |
式中:${{\mathop{ Re}\nolimits} _{{\rm{ns}}}}$—无滑脱雷诺数,无因次;${\rho _{{\rm{ns}}}}$—无滑脱密度,kg/m3;${\mu _{{\rm{ns}}}}$—无滑脱黏度,Pa⋅s。
无滑脱密度和无滑脱黏度的计算公式分别为
| $ {\rho _{{\rm{ns}}}} = {\rho _{\rm{g}}}\dfrac{{{v_{{\rm{sg}}}}}}{{{v_{\rm{m}}}}} + {\rho _{\rm{l}}}\left( {1 - \dfrac{{{v_{{\rm{sg}}}}}}{{{v_{\rm{m}}}}}} \right)$ | (21) |
| ${\mu _{{\rm{ns}}}} = {\mu _{\rm{g}}}\dfrac{{{v_{{\rm{sg}}}}}}{{{v_{\rm{m}}}}} + {\mu _{\rm{l}}}\left( {1 - \dfrac{{{v_{{\rm{sg}}}}}}{{{v_{\rm{m}}}}}} \right)$ | (22) |
式中,式中,${\mu _{\rm{g}}}$—气相黏度,Pa⋅s。
气液间表面张力按活性剂临界胶束浓度CMC下的表面张力计算,天然气偏差系数、黏度采用文献[17]推荐方法计算。
3 模型评价选用鄂尔多斯和川南39 口产水气井泡排时的井筒测压数据对新模型进行评价,同时参与对比的还有均质泡沫流模型和Ansari 多相流机理模型。其中泡排井数据范围如下:油压4.12∼16.55 MPa,井底压力5.42∼29.02 MPa,产气量3 130∼43 200 m3/d,产液量0.12∼50.00 m3/d,油管内径50.7∼76.0 mm,井深1 242∼3 654 m,地层水相对密度1.02∼1.05,气体相对密度平均为0.58∼0.65,加药浓度均达到临界胶束浓度。依据本文方法判断泡排井的流型涵盖了泡状流、段塞流、均质泡沫流和雾状流。图 1 为3 种模型计算井底压力与实测井底压力对比图。
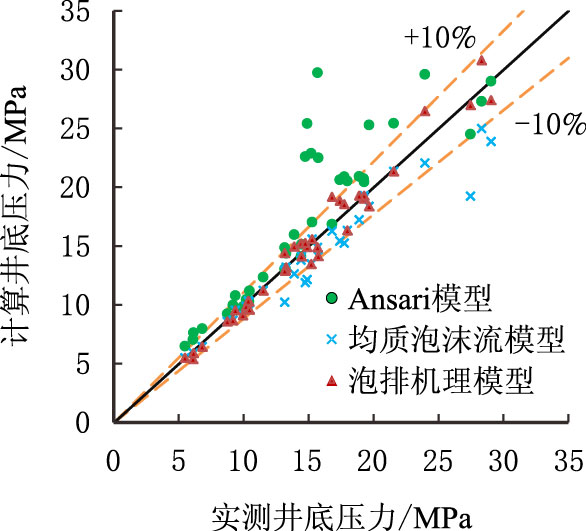 |
| 图1 井底压力计算值与实测值对比 Fig. 1 Comparison of measured and predicted bottomhole pressures |
由图可知,本文提出的泡排机理模型所预测的泡排井井底压力与实测值较为吻合,平均相对误差仅为-0.55%,而且离散度较低。而Ansari 机理模型和均质泡沫流模型误差分别为15.85% 和-6.88%。Ansari 机理模型预测值偏高,这是因为它没有考虑均质泡沫流型的存在,过高估计了气液间的滑脱效应。均质泡沫流模型低估了泡排井的实际压降,这是由于它没有考虑低气流速下泡状流和段塞流型的存在,低估了气液滑脱效应。
4 气液比敏感性分析以一口泡排示例井为例,利用本文模型对不同气液比(Gas Liquid Ratio,GLR)进行敏感性分析。假定该井连续加注起泡剂,加药浓度为临界胶束浓度,油管中流体能够连续生产,油压8 MPa,产水量40 m3/d,油管内径62 mm,井深3 000 m,井口温度20 ℃,井底温度90 ℃,地层水相对密度为1.02,气体相对密度为0.65,油管绝对粗糙度为0.015 24 mm,分析气液比在200∼2 500 m3/m3 范围内变化时的井筒流型分布和压力分布。
由图 2 可知,当GLR 较低为200 m3/m3 时,在井筒下段出现段塞流和泡状流,滑脱损失明显,井筒压耗较多;当GLR 在300∼1 200 m3/m3 时,整个井筒呈现均质泡沫流,此时气液间无滑脱,井筒压耗较低,是泡排最有利的流型。当GLR 增加到2 500 m3/m3 时,井筒完全呈现雾状流,即使不泡排气井也具有强的携液能力,井筒压耗较低。由图还说明,对于井底存在泡状流或段塞流的泡排井,通过适当注气提高气液比,可使泡排井流型转变为最佳的泡沫流型,减小滑脱损失,提高举升效率。
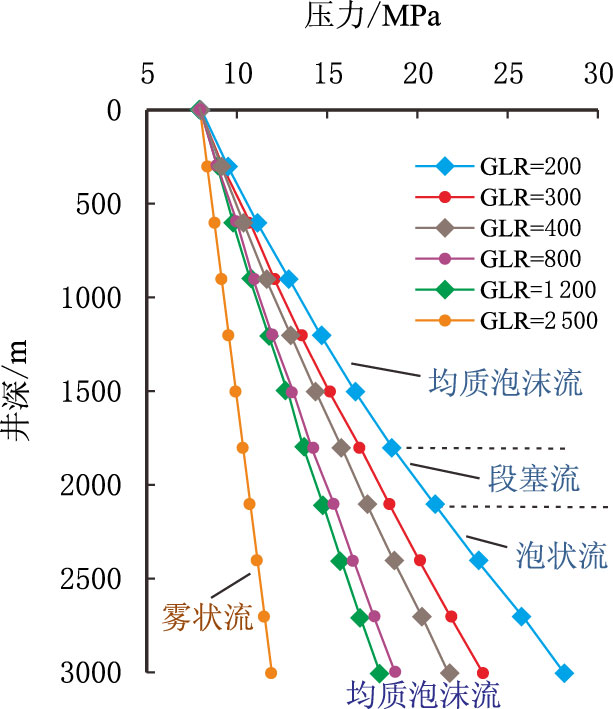 |
| 图2 不同气液比下井筒流型、压力分布 Fig. 2 Flow pattern and pressure profiles under different gas-liquid ratio |
(1)基于基本物理原理建立了适用于多种流型的泡排井多相流机理模型,模型将泡排井流型分为泡状流、段塞流、均质泡沫流和雾状流,能够预测泡排井流型并计算各流型的持液率和压降。
(2)流型预测模型由Mitchell B J 和Taitel Y 等的实验得到,重点考虑了含气率对泡沫流型的影响。泡状流、段塞流压降采用漂移模型计算,均质泡沫流压降采用均质幂律流体模型描述,而雾状流压降采用无滑脱模型计算。
(3)利用包含多种流型的泡排井实测压降数据对模型进行评价表明,新模型平均误差仅为-0.55%,满足工程精度需要。
(4)低气液比泡排井的井筒可能呈现泡状流或段塞流,适当补充注气可将流型改变为均质泡沫流,减小滑脱损失,提高举升效率。
| [1] | 蒋泽银, 唐永帆, 石晓松, 等. 中21井泡沫排水技术研究及效果评价[J]. 天然气工业, 2006, 26 (7) : 97 –99. |
| [2] |
李兆敏, 王登庆, 黄善波. 泡沫流体在井筒内流动时的耦合数学模型[J].
西南石油大学学报:自然科学版, 2008, 30 (6) : 1 –4.
Li Zhaomin, Wang Dengqing, Huang Shanbo. The coupling mathematical model for foam fluid flowing in well-bore[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2008, 30 (6) : 1 –4. |
| [3] |
李松岩, 李兆敏, 林日亿. 泡沫举升排酸过程井筒压力温度数学模型研究[J].
西南石油大学学报:自然科学版, 2009, 31 (2) : 59 –63.
Li Songyan, Li Zhaomin, Lin Riyi. Mathematical model of temperature and pressure distribution in wellbore during foam fluid lift acid drainage[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2009, 31 (2) : 59 –63. |
| [4] |
王冠华, 李兆敏. 泡沫在井简中流动的水力计算新方法[J].
燕山大学学报, 2009, 33 (4) : 363 –367.
Wang Guanhua, Li Zhaomin. A new method on wellbore hydraulic calculating of foam fluid[J]. Journal of Yanshan University, 2009, 33 (4) : 363 –367. |
| [5] | 王海涛, 伊向艺, 卢渊. 井筒气-液两相垂直管流的研究现状[J]. 试采技术, 2007, 27 (4) : 26 –28. |
| [6] | Brill J P, Mukherjee H. Multiphase flow in wells[M]. Richardson, Texas: Henry L. Doherty Memorial Fund of AIME, Society of Petroleum Engineers, 1999 . |
| [7] | Mitchell B J. Viscosity of foam[D]. Norman:University of Oklahoma, 1960. |
| [8] | Taitel Y, Bornea D, Dukler A E. Modelling flow pattern transitions for steady upward gas-liquid flow in vertical tubes[J]. AIChE Journal, 1980, 26 (3) : 345 –354. DOI:10.1002/(ISSN)1547-5905 |
| [9] | Khasanov M, Khabibullin R, Krasnov V, et al. A simple mechanistic model for void-fraction and pressure-gradient prediction in vertical and inclined gas/liquid flow[J]. SPE Production & Operations, 2009, 24 (1) : 165 –170. |
| [10] | Ansari A M, Sylvester N D, Sarica C, et al. A comprehensive mechanistic model for upward two-phase flow in wellbores[J]. SPE Production & Facilities, 1994, 9 (2) : 143 –151. |
| [11] | Zuber N, Hench J. Steady state and transient void fraction of bubbling systems and their operating limits(Part I, Steady State Operation)[R]. Washington DC:General Electric Report 62GL100, 1962. |
| [12] | Jain A K. An accurate explicit equation for friction factor[J]. Journal of the Hydraulics Division, 1976, 102 (5) : 674 –677. |
| [13] | Hasan A R, Kabir C S, Sayarpour M. Simplified twophase flow modeling in wellbores[J]. Journal of Petroleum Science and Engineering, 2010, 72 (1) : 42 –49. |
| [14] | Godbole P V, Tang C C, Chajar A J. Correlations for different flow patterns in upward vertical two-phase flow[J]. Heat Transfer Engineering, 2011, 32 (10) : 843 –860. DOI:10.1080/01457632.2011.548285 |
| [15] | Govier G W, Aziz K. The flow of complex mixtures in pipes[M]. Texas: Society of Petroleum Engineers, 2008 . |
| [16] | Metzner A B, Reed J C. Flow of non-newtonian fluids-correlation of the laminar, transition, and turbulentflow regions[J]. AIChE Journal, 1955, 1 (4) : 434 –440. DOI:10.1002/(ISSN)1547-5905 |
| [17] | 李士伦. 天然气工程[M]. 北京: 石油工业出版社, 2008 . |
 2014, Vol. 26
2014, Vol. 26

