页岩气作为常规油气的替代能源,目前已经成为开发的热点,而掌握页岩储层孔隙介质中的流体流动行为和流动规律对提高页岩气开发具有重要意义。对于页岩储层来说,由于基质的孔隙较小,孔隙直径只有纳米级[1-2],基质渗透率低至微达西到纳达西[3-4],需要压裂改造才可获得经济产量[5]。页岩气在储层中表现为从纳米孔隙的微观流到宏观水力裂缝的达西流多种流态,特别是当页岩基质中气体分子与管壁间的碰撞更为频繁时,气体流动表现为分子级的微观流态,经典达西流动模型不再具有适应性,已无法用于页岩气流动模拟分析[6-8],但滑脱流与克努森扩散这两种机制可解释页岩气藏实际产量高于预测产量[9]。对于页岩储层流体渗流机理的描述[10-13],许多学者提出了多种数学模型[14-20]对页岩气藏渗流机理的进行模拟[21-25],但都是建立在对黏性流动模型的修正或者在黏性流模型加上简单附加分子流动项,无法完全客观地表征多尺度页岩气的流体特征。本文基于表观渗透率的定义[26-27],考虑页岩储层存在从黏性流、滑移流、过渡流到分子自由流的不同流态,建立了多尺度页岩介质的流动分析模型,计算分析了各个影响因素及流动规律。
1 气体流动的流态划分对于常规油气藏来说,达西流动方程能够描述油藏流体的流动状态,但对于超低渗透储层的页岩气藏,随孔隙半径的不断降低,流体将从达西流向其他流态转化,这时分子与孔隙壁面的相互碰撞几率较分子间的碰撞更为频繁,这种作用效应对流体传输具有更重要的影响,随着孔隙流体压力的降低,这样作用效应将促使储层的表观渗透率进一步增加。早在1909 年Knudsen 就完成了稀薄气体动力学的研究工作,用克努森数($K_{\rm{n}}$ 数)对气体在不同尺度管道的流动进行了分区,定义$K_{\rm{n}}$ 数为[16]
| ${K_{\rm{n}}} = \dfrac{\lambda }{L}$ | (1) |
式中:$\lambda$—气体分子平均自由程,m;L—流动特征长度,m。
根据$K_{\rm{n}}$ 数的大小,将流动划分为4 个不同的流动区域[17]:$K_{\rm{n}}$ 6 0:001 为黏性流;0:001 < $K_{\rm{n}}$ 60:100 为滑移流;0:100 < $K_{\rm{n}}$ < 10:000 为过渡流;$K_{\rm{n}}$ > 10:000 为自由分子流。
正确定义分子平均自由程对计算$K_{\rm{n}}$ 非常重要。理想气体是一种实际上不存在的假想气体,其分子是有弹性、不占据空间体积的质点,分子相互间没有作用力。页岩中CH4 气体等分子直径与页岩纳米孔隙相比不可忽略时,气体分子本身占据一定的体积,分子之间存在相互作用,同时分子具有一定的可压缩性必须加以考虑。为此页岩储层中的气体不能考虑为理想状态,真实气体的状态方程和真实气体的密度方程分别为:
| $pV = Zn{\rm{R}}T$ | (2) |
| $\rho = \dfrac{{p{M_{\rm{g}}}}}{{Z{\rm{R}}T}}$ | (3) |
式中:
p—压力,Pa;
V—体积,m3;
Z—压缩因子,无因次;
n—为物质的量,mol;
R—气体常数,R = 8.314 J/(mol⋅K);
T —温度,K;
$\rho$—气体密度,kg/m3;
$M_{\rm{g}}$—分子质量,kg/mol。
结合实际情况,真实气体分子平均自由程定义为[25]
| $\lambda = \sqrt {\dfrac{{{\rm{\pi }}Z{\rm{R}}T}}{{2{M_{\rm{g}}}}}} \dfrac{\mu }{p}$ | (4) |
式中:$\mu$—黏度,Pa⋅s。
2 不同流态的流动方程首先建立不同流态的流动质量通量方程,在此基础上推导得到表观渗透率计算模型。
2.1 黏性流当流动空间的特征长度(如水力裂缝、微裂缝和大的孔隙)远大于分子平均自由程时,气体分子与孔壁间的碰撞概率远小于气体分子间的碰撞概率,此时气体的流动过程为传统的黏性流。气体流动过程中存在的压力梯度所引起的黏性流动采用达西定律来描述,质量通量为
| ${N_{\rm{V}}} = - \left( {\dfrac{{{K_{\rm{D}}}}}{\mu }\dfrac{{p_{\rm{a}}{M_{\rm{g}}}}}{{Z{\rm{R}}T}}} \right)\nabla p$ | (5) |
式中:${N_{\rm{V}}}$黏性质量通量,kg/(s${\cdot}m^2$); ${K_{\rm{D}}}$—达西渗透率,m2; ${p_{\rm{a}}}$—平均压力,Pa。
圆管的达西渗透率表示为[26]
| ${K_{\rm{D}}} = \dfrac{{{r^2}}}{8}$ | (6) |
式中:r—孔隙半径,m。
2.2 滑移流随着流动空间尺度减小,当$K_{\rm{n}}$ 数增加到0.001∼0.100 时,流动表现为滑移流,由于孔隙壁面上的滑移速度对气体流动有加速作用,需要对黏性流进行滑移校正,引入一个无因次滑移系数B 来校正孔隙中的滑移流[27]。
| $B = 1 + {\left( {\dfrac{{8{\rm{\pi R}}T}}{{{M_{\rm{g}}}}}} \right)^{0.5}}\dfrac{\mu }{{{p_{\rm{a}}}r}}\left( {\dfrac{2}{\alpha } - 1} \right)$ | (7) |
式中:B—滑移系数,无因次;$\alpha$—切向动量调节系数,无因次,其值理论上在0∼1 变化,与孔隙壁面光滑度、气体类型、温度和压力有关。
2.3 分子自由流当流动空间的特征长度减小到$K_{\rm{n}}$ 数大于10.000 时气体流动表现为分子自由流,此时气体分子以单个分子自由运动的形式通过通道而不是以分子群形式流过通道。纳米孔隙中气体的分子自由流质量通量为[9]
| ${N_{\rm{F}}} = - \dfrac{{{M_{\rm{g}}}{D_{\rm{K}}}}}{{{\rm{R}}T}}\nabla p$ | (8) |
式中:${D_{\rm{K}}}$—克努森扩散系数,m2/s;${N_{\rm{F}}}$—自由分子质量通量,kg/(s⋅m2)。
克努森扩散系数${D_{\rm{K}}}$ 定义为
| ${D_{\rm{K}}} = \dfrac{{2r}}{3}{\left( {\dfrac{{8{\rm{R}}T}}{{\pi {M_{\rm{g}}}}}} \right)^{1/2}}$ | (9) |
当流动空间的特征长度减小到$K_{\rm{n}}$ 数为0.100∼10.000 时,这时候气体流动表现为分子自由流与黏性流之间的一种过渡状态,称为过渡流。目前对过渡流的一般采用两种方式来表征,一种是将黏性流用滑移项加以校正,另一种方法是结合黏性流与分子自由流,将黏性流与Knudsen 扩散综合表征过渡流动,但是结果比黏性流与Knudsen 扩散都低[21],而过渡流是介于它们之间的一个流动,用该方法来表示过渡流显然不太适用。Adzumi 实验研究指出由于黏性流[19],Knudsen 扩散以及介于它们之间的流动(过渡流)的作用,不同$K_{\rm{n}}$ 数下流动公式并非统一。为了表征过渡流的贡献,Adzumi 引入一个贡献系数来表示不同流动机理的贡献,表达为
| ${N_{\rm{t}}} = (1 - \varepsilon ){N_{\rm{V}}} + \varepsilon {N_{\rm{F}}}$ | (10) |
式中:${N_{\rm{t}}}$—过渡流的质量通量,kg/(s⋅m2);"—贡献系数,无因次。
贡献系数计算公式为
| $\varepsilon = {{\rm{C}}_{\rm{A}}}{\left[ {1 - \exp \left( {\dfrac{{ - {K_{\rm{n}}}}}{{{{{K}}_{{\rm{nVisc}}}}}}} \right)} \right]^{\rm{S}}}$ | (11) |
式中:$K_{\rm{nVisc}}$—从纯黏性流到拟扩散流开始过渡的Knudsen数,一般为0.3;${\rm{C}}_{\rm{A}}$—常数,一般为1.0;${\rm{S}}$—常数,一般取1。
3 表观渗透率计算方程由以上分析页岩储层内流体的黏性流、滑移流、过渡流和分子自由流可得,以传统黏性流为基础并加以滑移校正,结合分子自由流,再引入贡献系数用于表征过渡流,可统一不同尺度下的不同流动得出多尺度页岩储层总质量通量为
| ${N_{\rm{t}}} = (\varepsilon -1 )B\left( {\dfrac{{{r^2}}}{{8\mu }}\dfrac{{\bar p{M_{\rm{g}}}}}{{Z{\rm{R}}T}}} \right)\nabla p - \varepsilon \dfrac{{{M_{\rm{g}}}}}{{{\rm{R}}T}}\dfrac{{2r}}{3}{\left( {\dfrac{{8{\rm{R}}T}}{{{\rm{\pi }}{M_{\rm{g}}}}}} \right)^{1/2}}\nabla p$ | (12) |
由达西方程所定义的质量通量为
| ${N_{\rm{D}}} = - \left( {\dfrac{{{K_{\rm{D}}}{\rho _{\rm{a}}}}}{\mu }} \right)\nabla p$ | (13) |
式中:$\rho _{\rm{a}}$—平均密度,kg/m3。
将多尺度页岩储层的质量通量表达式(12)表述为式(13)的形式,为
| ${N_t} = - \left( {\dfrac{{{K_{\rm{A}}}{\rho _{\rm{a}}}}}{{\rm{\mu }}}} \right)\nabla p$ | (14) |
其中,${K_{\rm{A}}}$ 为表观渗透率
| ${K_{\rm{A}}} = (1 - \varepsilon )B\dfrac{{{r^2}}}{8} + \varepsilon \dfrac{{2r{M_{\rm{g}}}\mu }}{{3{\rm{R}}T{\rho _{\rm{a}}}}}{\left( {\dfrac{{8{\rm{R}}T}}{{{\rm{\pi }}{M_{\rm{g}}}}}} \right)^{1/2}}$ | (15) |
由式(6)和式(15)可得表观渗透率与达西渗透率的比值为
| ${K_{\rm{A}}}/{K_{\rm{D}}} = (1 - \varepsilon )B + \varepsilon \dfrac{{2{M_{\rm{g}}}\mu }}{{3{\rm{R}}T{\rho _{\rm{a}}}}}{\left( {\dfrac{{8{\rm{R}}T}}{{{\rm{\pi }}{M_{\rm{g}}}}}} \right)^{1/2}}\dfrac{8}{r}$ | (16) |
基于以上建立的页岩气流动计算模型,对其影响因素进行了计算分析。采用基本参数为生产压差:7 MPa;地层泄油半径:100 m;地层温度:350 K;分子摩尔质量;16 kg/kmol;地层平均压力:24 MPa;气体黏度:4.1$\times$10$^{-2}$~mPa$\cdot$s。
图 1 为孔喉半径对$K_{\rm{n}}$ 数及贡献系数的影响,由图可知,孔隙半径越小,$K_{\rm{n}}$ 数及微观流动量的贡献系数都越大,孔喉半径大于100 nm,$K_{\rm{n}}$ 数小于0.010,这时页岩气的微观流动量非常小,可忽略不计,此时可认为页岩气为黏性流;孔隙半径小于4 nm 后页岩气的微观流动贡献系数接近1,反映此时页岩气的微观流动在孔隙中为主要流动形式。
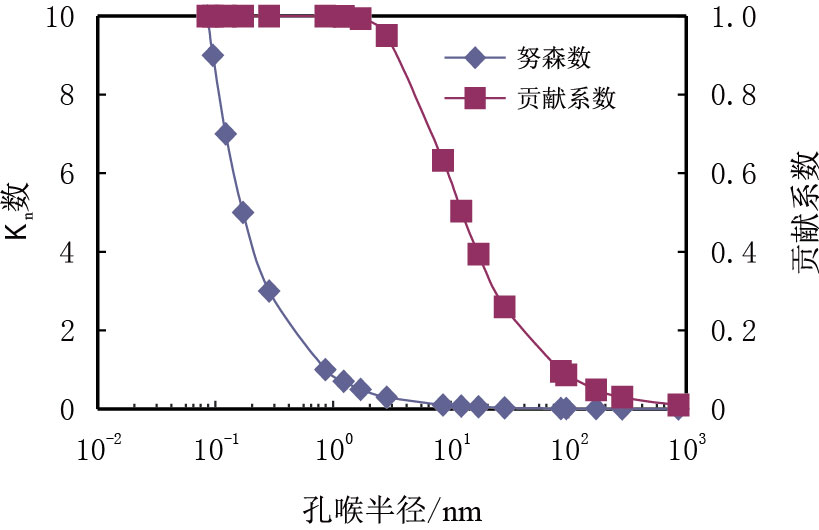 |
| 图1 $K_{\rm{n}}$ 数与贡献系数随孔喉半径的变化图 Fig. 1 The curves of $K_{\rm{n}}$ number and the contribution coefficient variation with the pore throat radius |
图 2 是分子扩散量与总流量的比值随多孔介质孔隙半径的变化图,从该图可看出,存在一个临界孔喉半径,在孔喉半径大于100 nm 时,分子扩散量占总流量比例小于1%,从而可忽略,小于该孔隙半径时并随着孔喉半径的减小,分子流量的比例将会不断上升。由于传统多孔介质流动模型并不包含分子流动,如果对页岩储层的产量预测采用传统渗流模型将导致一定误差,特别是过渡流与分子流对产能的贡献大于黏性流时误差将变得严重。
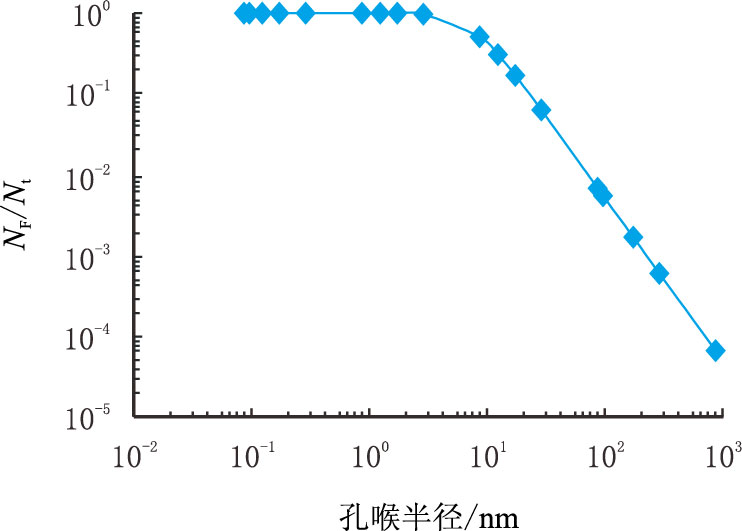 |
| 图2 分子流动占总流动比例随孔喉半径变化 Fig. 2 The molecular mobility to total flow ratio curve changes with the pore throat radius |
图 3 为页岩气分子的摩尔质量对分子扩散流量与总流量之比的影响,从图中可见,分子摩尔质量越小,分子流动的贡献能力越大,且孔隙半径越小,增加速率越大。这主要是由于分子摩尔质量越小,单个分子质量越小,分子移动越容易,分子与孔隙壁面发生碰撞的几率增加,且孔隙越小,碰撞的频率越大,则更易表现为微观流态。
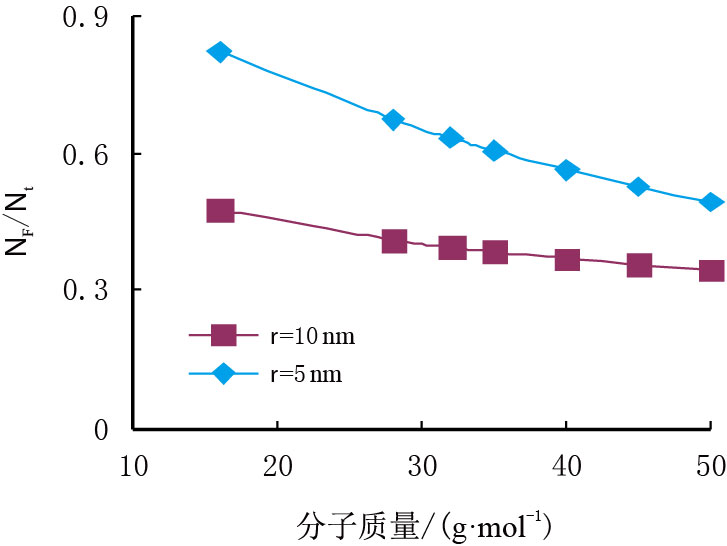 |
| 图3 分子流动占总流动比例随分子摩尔质量变化图 Fig. 3 The molecular mobility to total flow ratio with the molecular molar mass variation |
图 4 为表观渗透率与达西渗透率的比值随页岩介质孔隙半径的变化图,由图中可看出,孔隙半径越小则表观渗透率与达西渗透率的比值越大,微观流的贡献越大,该结论可以合理解释致密页岩气藏生产时实际产量高于常规渗流模型预测的产量,为此,对于页岩储层来说,选择考虑微观流态下的表观渗透率模型预测页岩气藏产量可能更为接近实际产量。
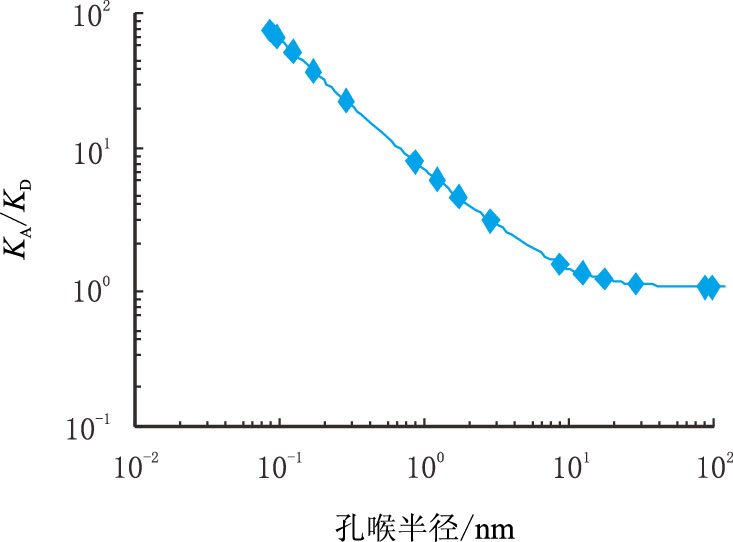 |
| 图4 表观渗透率与达西渗透率之比随孔喉半径变化图 Fig. 4 The apparent permeability and Darcy permeability ratio changes with the pore throat radius diagram |
图 5 为孔喉半径为10 nm 下,表观渗透率与达西渗透率的比值随压力的变化关系,由图可见,压力越低则表观渗透率与达西渗透率的比值越大,而温度对它的影响力则非常有限。在生产过程中随气藏压力不断降低,表观与达西渗透率的比值不断增加,从而可减缓页岩气产量的下降速率,该效应对页岩气的生产具有重要的指导作用。
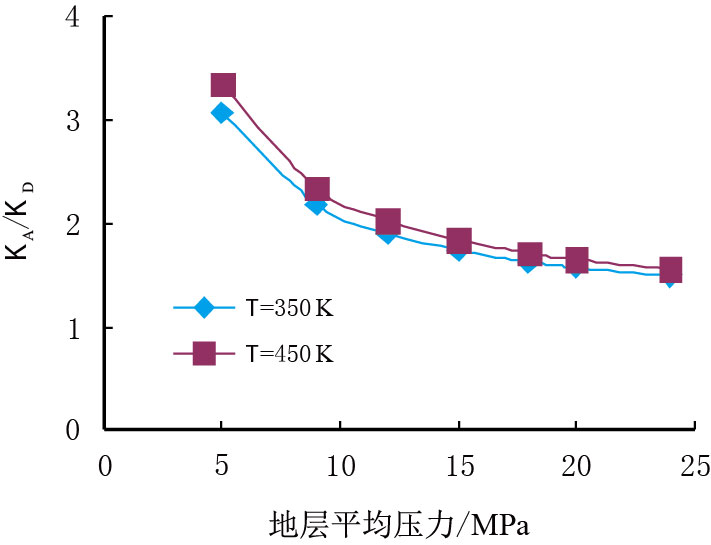 |
| 图5 表观渗透率与达西渗透率比值随压力变化图 Fig. 5 The apparent permeability and Darcy permeability ratio changes with the pressure diagram |
(1)基于表观渗透率定义,结合不同流态的作用效应,建立了基于黏性流、滑移流、过渡流和分子自由流的表观渗透率计算统一方程,揭示了页岩气藏生产时实际产量高于达西模型预测产量的本质原因。
(2)计算分析表明,页岩储层的孔隙越小、气体分子摩尔质量越小、地层压力越低,则气体越易表现为微观流态,这时表观渗透率与达西渗透率的比值越大,采用达西流动模型预测的产量误差则越大。对于多尺度的页岩储层来说,需考虑页岩气的微观流动行为对井产量的影响,采用文中模型可提高页岩气藏产量预测的准确性和可靠性。
| [1] | Curtis M E, Ambrose R J, Sondergeld C H, et al. Structural characterization of gas shales on the micro-and nanoscales[C]. SPE 137693, 2010. |
| [2] | Elgmati M,Zhang H,Bai B J,et al. Submicron-pore characterization of shales gas plays[C]. SPE 144050, 2011. |
| [3] | Yang Feng,Ning Zhengfu,Wang Qing,et al. Integrated study of reservoir characteristics of a shale gas reservoir:A case study from Sichuan Basin of China[C]. SPE 165870, 2013. |
| [4] | Elgmati M, Zobaa M, Zhang H, et al. Palynofacies analysis and submicron pore modeling of shale-gas plays[C]. SPE 144267, 2011. |
| [5] |
赵金洲, 任岚, 胡永全. 页岩储层压裂缝成网延伸的受控因素分析[J].
西南石油大学学报:自然科学版, 2013, 35 (1) : 1 –9.
Zhao Jinzhou, Ren Lan, Hu Yongquan. Controlling factors of hydraulic fractures extending into network in shale formations[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2013, 35 (1) : 1 –9. |
| [6] | Fathi E, Yucel Akkutlu I. Lattice boltzmann method for simulation of shale gas transport in Kerogen[C]. SPE 146821, 2011. |
| [7] | Yan B, Alfi M, Wang Y, et al. A new approach for the simulation of fluid flow in unconventional reservoirs through multiple permeability modeling[C]. SPE 166173, 2013. |
| [8] | Darishchev A,Nancy E N S G,Lemouzy P,et al. On simulation of flow in tight and shale gas reservoirs[C]. SPE 163990, 2013. |
| [9] | Javadpour F, Fisher D, Unsworth M. Nanoscale gas flow in shale gas sediments[J]. Journal of Canadian Petroleum Technology, 2007, 46 (10) : 55 –61. |
| [10] |
李晓强, 周志宇, 冯光, 等. 页岩基质扩散流动对页岩气井产能的影响[J].
油气藏评价与开发, 2011, 5 (1) : 67 –70.
Li Xiaoqiang, Zhou Zhiyu, Feng Guang, et al. The impact of shale matrix diffusion on shale gas capacity[J]. Reservoir Evaluation and Development, 2011, 5 (1) : 67 –70. |
| [11] |
于荣泽, 卞亚南, 张晓伟, 等. 页岩储层流动机制综述[J].
科技导报, 2012, 30 (24) : 75 –79.
Yu Rongze, Bian Yanan, Zhang Xiaowei, et al. A review of flow mechanisms in shale gas reservoir[J]. Science & Technology Review, 2012, 30 (24) : 75 –79. |
| [12] |
魏云, 赵自斌. 页岩气藏的渗流机理[J].
辽宁化工, 2013, 42 (2) : 152 –153.
Wei Yun, Zhao Zibin. Percolation mechanism of shale gas[J]. Liaoning Chemical Industry, 2013, 42 (2) : 152 –153. |
| [13] |
郭为, 熊伟, 高树生, 等. 页岩纳米级孔隙气体流动特征[J].
石油钻采工艺, 2012, 34 (6) : 57 –60.
Guo Wei, Xiong Wei, Gao Shusheng, et al. Gas flow characteristics in shales nanopores[J]. Oil Drilling & Production Technology, 2012, 34 (6) : 57 –60. |
| [14] |
李治平, 李智锋. 页岩气纳米级孔隙渗流动态特征[J].
天然气工业, 2012, 32 (4) : 50 –53.
Li Zhiping, Li Zhifeng. Dynamic characteristics of shale gas flow in nanoscale pores[J]. Natural Gas Industry, 2012, 32 (4) : 50 –53. |
| [15] | Shabro V, Torres-Verdín C, Javadpour F. Numerical simulation of shale-gas production:from pore-scale modeling of slip-flow,knudsen diffusion,and langmuir desorp-tion to reservoir modeling of compressible fluid[C]. SPE 144355, 2011. |
| [16] | Beskok A, Karniadakis G E. A model for flows in channels,pipes,and ducts at micro and nano scales[J]. Microscale Thermophysical Engineer, 1999, 3 (1) : 43 –77. DOI:10.1080/108939599199864 |
| [17] | Faruk Civan. Effective correlation of apparent gas permeability in tight porous media[J]. Transport in Porous Media, 2010, 82 (2) : 375 –384. DOI:10.1007/s11242-009-9432-z |
| [18] | Faruk Civan,Deepak Devegowda,Richard Sigal. Critical evaluation and improvement of methods for determination of matrix permeability of shale[C]. SPE 166473, 2013. |
| [19] | Mohammad R R, Aguilera R, Kantzas A. A new unified diffusion viscous flow model based on pore level studies of tight gas formations[C]. SPE 149223, 2011. |
| [20] | Sakhaee-Pour A, Steven L B. Gas permeability of shale[C]. SPE 146944, 2011. |
| [21] |
王瑞, 张宁生, 刘晓娟, 等. 页岩气扩散系数和视渗透率的计算与分析[J].
西北大学学报:自然科学版, 2013, 43 (1) : 75 –88.
Wang Rui, Zhang Ningsheng, Liu Xiaojuan, et al. The calculation and analysis of diffusion coefficient and apparent permeability of shale gas[J]. Journal of Northwest University:Natural Science Edition, 2013, 43 (1) : 75 –88. |
| [22] |
姚军, 孙海, 樊冬艳, 等. 页岩气藏运移机制及数值模拟[J].
中国石油大学学报, 2013, 37 (1) : 91 –98.
Yao Jun, Sun Hai, Fan Dongyan, et al. Transport mechanisms and numerical simulation of shale gas reservoirs[J]. Journal of China University of Petroleum:Natural Science Edition, 2013, 37 (1) : 91 –98. |
| [23] |
程远方, 董丙响, 时贤, 等. 页岩气藏三孔双渗模型的渗流机理[J].
天然气工业, 2012, 32 (9) : 44 –46.
Cheng Yuanfang, Dong Bingxiang, Shi Xian, et al. Seepage mechanism of a triple-porosity/dual-permeability model for shale gas reservoirs[J]. Natural Gas Industry, 2012, 32 (9) : 44 –46. |
| [24] | Hassan Dehghanpour, Mahdy Shirdel. A triple porosity model for shale gas reservoirs[C]. SPE 149501, 2011. |
| [25] | Shi Juntai,Zhang Lei,Li Yuansheng,et al. Diffusion and flow mechanisms of shale gas through matrix pores and gas production forecasting[C]. SPE 167226, 2013. |
| [26] | Michel G G,Sigal R F,Civan F,et al. Parametric investigation of shale gas production considering nano-scale pore size distribution, formation factor, and non-darcy flow mechanisms[C]. SPE 147438, 2011. |
| [27] | Javadpour F. Nanopores and apparent permeability of gas flow in mudrocks(shales and siltstone)[J]. Journal of Canadian Petroleum Technology, 2009, 48 (8) : 16 –21. DOI:10.2118/09-08-16-DA |
 2014, Vol. 26
2014, Vol. 26

