2. 中国石油大学(北京)CNPC 物探重点实验室, 北京 昌平 102249
2. CNPC Key Laboratory of Geophysical Exploration, China University of Petroleum(Beijing), Changping, Beijing 102249, China
地震波在地下介质中传播时,能量会发生衰减,造成的因素主要分为两类:非固有衰减和固有衰减。其中,非固有衰减包括几何扩散、反射透射损失、层间颗粒散射等,这种衰减一般认为与频率无关;固有衰减则是地层的吸收作用,频率越高,吸收越严重,同时由于速度频散原因,地震子波的相位发生改变。固有衰减造成地震波主频降低、带宽减小,严重影响了中深层地震资料的成像能力。品质因子Q是表征地层对地震波吸收衰减强弱的常用参量,Q值越小,衰减作用越强。反Q补偿是提高资料分辨率的一种有效手段,需要提取准确的地下Q场。另外,当地层含气时,Q值将变小,呈现出较为明显的异常。因此,Q值的准确估算对于高精度解释、储层预测及油藏描述等具有重要的意义[1]。
常规的品质因子估算方法[2-3]分两大类:时间域和频率域。时间域方法有上升时间法[4]、解析信号法[5]等,可以利用时间信号直接计算,但受资料品质等因素影响较大,而且只能利用局部一小段信息。频率域方法有谱比法(LSR)、质心频移法(CFS)[6-9]、峰值频率法[10-13]等,一般认为频率域方法比较稳定,可靠性高[14-20]。质心法是目前应用较多的Q值估算方法,其利用了频谱的统计属性(质心和带宽),通过两者的解析组合来反演品质因子,具有较好的鲁棒性。武银婷等[21]对质心法进行了测试,认为该方法比频谱比法、振幅衰减法能更加准确识别薄层界面;张大伟等[22]通过模型对比、资料测试等分析认为,质心法的估算结果比谱比法更精确、更可信;赵宁等[23]从数学近似的角度推导了更为严密的属性组合法,与质心法类似,都是基于子波谱的统计属性组合式估算Q值,该方法规避了传统质心法对震源谱的Gauss函数假设,更利于误差控制及理论分析。但频域方法面临的问题是需要提取较为准确的地震子波谱,Q值估算精度很大程度上依赖于波谱的提取效果。
为了避免地震子波谱的提取,提出时间域质心频移法,在时间域信号上直接估算地震子波谱的质心和带宽,再根据质心频移公式估算品质因子Q。最后,利用VSP下行波场的模型记录,测试该方法的可信性。
1 基本原理Barnes A E[24]指出,对于一个常相位子波a(t),其包络(由Hilbert变换得到)峰值处的瞬时频率fs等于其振幅谱A(f)的质心频率fc
| $ {f_{\rm{s}}} = {f_{\rm{c}}} = \frac{{\int_{\rm{0}}^{ + \infty } {fA\left( f \right){\rm{d}}f} }}{{\int_{\rm{0}}^{ + \infty } {A\left( f \right){\rm{d}}f} }} $ | (1) |
式中:fs-包络峰值处的瞬时频率,Hz;fc-谱的质心频率,Hz。
给定一子波g(t),其振幅谱记为Gauss谱G(f)
| $ G\left( f \right) = \exp \left[{-\dfrac{{{{\left( {f-{f_{\rm{c}}}} \right)}^{\rm{2}}}}}{{{\rm{2}}\sigma _f^{\rm{2}}}}} \right] $ | (2) |
式中:σf-谱的半径(即带宽的一半),Hz。
事实上,Gauss谱具有较好的数学特性,根据Fourier反变换,g(t)的包络亦是一个Gauss函数,定义其中心为
| $ {t_0} = \dfrac{{\int_{ - \infty }^\infty {tg(t)\textrm{d}t} }}{{\int_{ - \infty }^\infty {g(t)\textrm{d}t} }} $ |
其半宽度为
| $ {\sigma _t} = {\left[{\dfrac{{\int_{-\infty }^\infty {{{(t-{t_0})}^2}g(t)\textrm{d}t} }}{{\int_{-\infty }^\infty {g(t)\textrm{d}t} }}} \right]^{\frac{1}{2}}} $ |
则有如下关系
| $ {{\sigma }_{t}}\cdot {{\sigma }_{f}}=\frac{1}{\text{2 }\!\!\pi\!\!\text{ }} $ | (3) |
记地震波传播过程中的初始子波谱为S(f),衰减子波谱为R(f),若不考虑相位频散因素,按Futterman模型,则有
| $ R\left( f \right)=S\left( f \right)\exp \left( -\frac{\text{ }\!\!\pi\!\!\text{ }\Delta t}{Q}f \right) $ | (4) |
质心频移法利用如下解析式进行Q值反演
| $ Q=\text{ }\!\!\pi\!\!\text{ }\Delta t\frac{\sigma _{\text{1}}^{\text{2}}}{{{f}_{\text{c1}}}-{{f}_{\text{c2}}}} $ | (5) |
式中:
fc1-初始子波谱S(f)的质心频率,Hz;fc2-衰减子波谱R(f)的质心频率,Hz;Δt-子波传播时差,s;Q-传播介质的品质因子,无因次。
对于近似Gauss谱的常相位子波,可以直接在时间域估算其包络峰值处的瞬时频率和包络宽度,联立式(1)、式(3)和式(5),得到Q值估算式
| $ Q=\frac{\Delta t}{\text{4 }\!\!\pi\!\!\text{ }}\frac{1}{{{f}_{\text{s1}}}-{{f}_{\text{s2}}}}\frac{1}{\sigma _{\text{t1}}^{\text{2}}} $ | (6) |
式中:
fs1,σt1-初始子波包络峰值处瞬时频率和半径,Hz;fs2-衰减子波包络峰值处瞬时频率,Hz。
式(6)即为时间域质心频移式。
2 模型测试 2.1 单子波测试对式(1)和式(3)进行单子波测试,选取的子波谱有Gauss谱和Ricker谱。图 1是Gauss谱子波,主频f0为50 Hz,谱半径σf取15 Hz,左图为时间域子波(蓝线为波形,红线为包络),右图为振幅谱(蓝线为振幅谱,“*”号为质心频率,红色实线间距表示波谱的带宽)。根据时间域复信号,利用式(1)估算出质心频率为50.02 Hz,谱半径为14.94 Hz,与理论值较为接近。图 2是Ricker谱子波,主频取40 Hz,图中各曲线说明同图 1。根据频率域振幅谱,可计算得到该谱的质心频率为45.13 Hz,谱半径为19.04 Hz;根据时间域复信号,可计算得到质心频率为45.11 Hz,谱半径为18.21 Hz,两组数值较为接近,相对误差在4.50%以内。
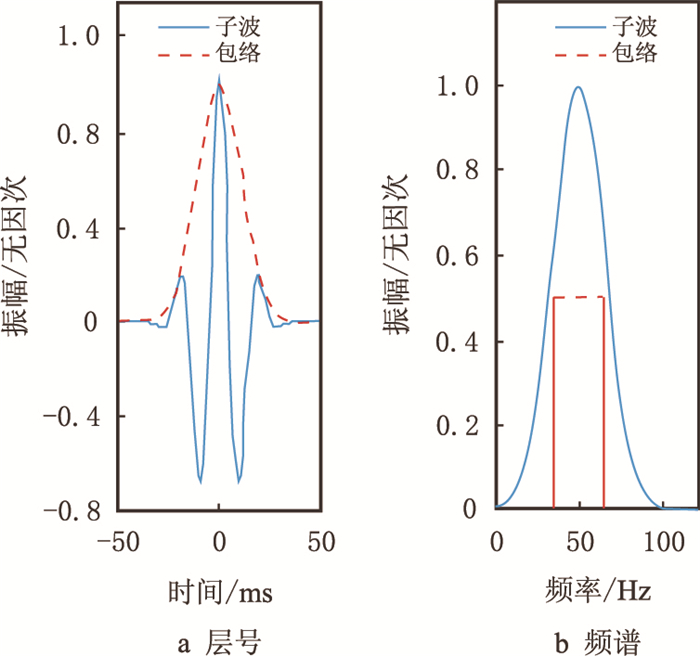 |
| 图1 Gauss谱子波 Fig. 1 Gauss function wavelet |
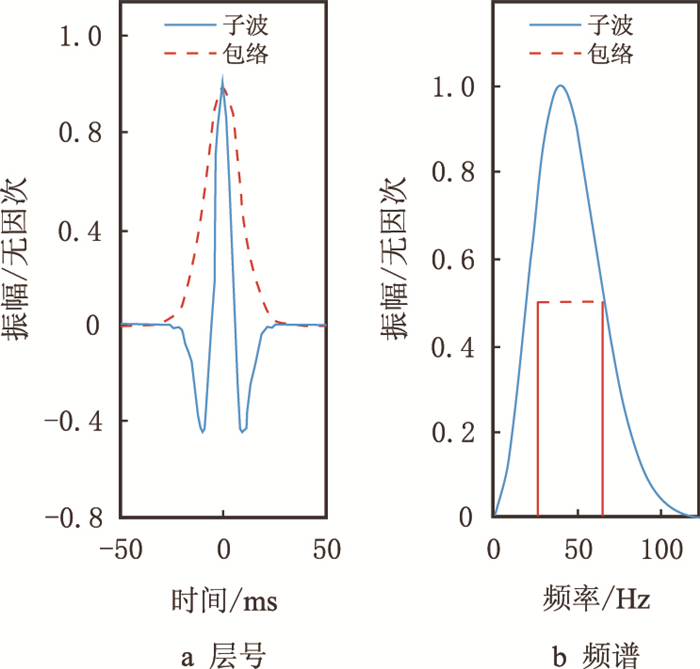 |
| 图2 Ricker谱子波 Fig. 2 Ricker wavelet |
为不失一般性,这里进行了多组不同主频Ricker谱(常相位值随机给定)的测试,分别从频率域和时间域估算质心和谱半径,估算结果见表 1。估算结果显示,时间域估算的质心频率与真实值之间的误差在0.15%以内,谱半径误差在4.50%以内。测试结果表明,对于近似Gauss谱的常相位子波,时间域估算的质心频率和谱半径具有一定的可信度。
| 表1 不同主频的Ricker子波质心频率和谱半径 Table 1 Centroid frequency and spectral radius of Ricker wavelets with different dominant frequencies |
设计一单层均匀介质,层速度为2 000 m/s,层厚为100 m,单层旅行时为0.05 s,品质因子为50。初始子波为50 Hz主频的Ricker子波(记为子波1),见图 3中蓝色实线,蓝色虚线为其包络;经介质衰减后的子波(记为子波2)见图 3中红色实线,红色虚线为其包络。根据时间域质心式可反演得Q值为46.56,接近于真实值50,相对误差在10%以内。如果采用频率域质心法,则反演得Q值为50.92,精度更高。对比两种方法发现,时间域求得的质心差为1.748 0Hz,谱半径为22.763 5 Hz,频率域质心差为1.748 8Hz,谱半径为23.809 7 Hz。试算结果可见,时间域质心式的精度稍低于常规质心法,误差主要来源于谱半径的估算,这是由Ricker谱与Gauss谱差异造成的。式(3)显示Gauss谱时频窗面积(即4σt·σf)为(2π)-1,达到了理论上的最小值(即时频分辨率的极限),常见波谱的时频窗面积一般都大于该值,造成谱半径估算误差。但应该肯定的是,时间域质心法反演的地层Q值,具有一定的可信度。
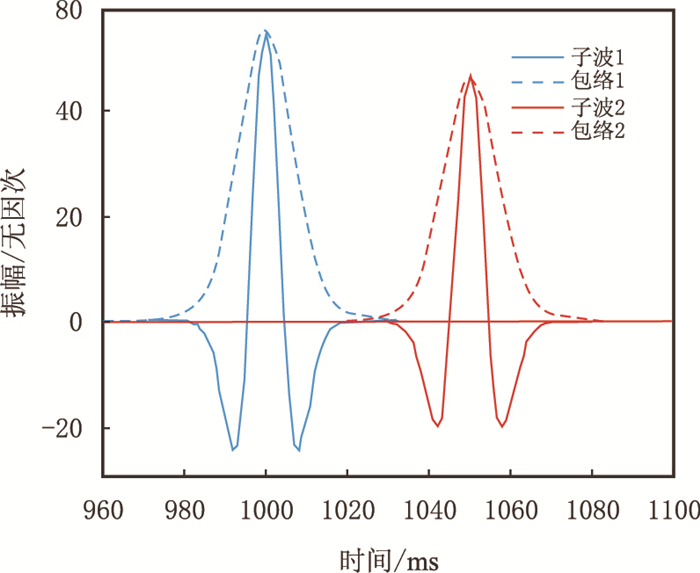 |
| 图3 衰减正演记录 Fig. 3 Attenuation of wavelet |
设计了一个5层水平介质模型,地层参数见表 2。地表初始子波选50 Hz主频的Ricker子波,按式(4)在地层中衰减,检波间距为10 m,得到图 4所示的零偏VSP下行波场。根据该下行波场,利用式(4)对相邻道进行Q值反演,由于初始子波为Ricker子波,估算谱半径σf时将式(3)中的(2π)-1改为0.166 5(该值根据Ricker子波的时频窗面积给定)。图 5是Q值反演结果,蓝线为真实值,红线为反演值。反演结果较好地反映了地层的Q值走向,在浅层,Q值较准确,随着传播深度的增加,Q值渐渐偏离真实值。图 6是相对误差曲线,相对误差在10%以内。如果初始子波时频窗面积未知,仍然按照式(3)估算谱半径,那么反演结果的相对误差将进一步扩大,在8 12%,但对地层Q值的相对趋势走向影响不大。
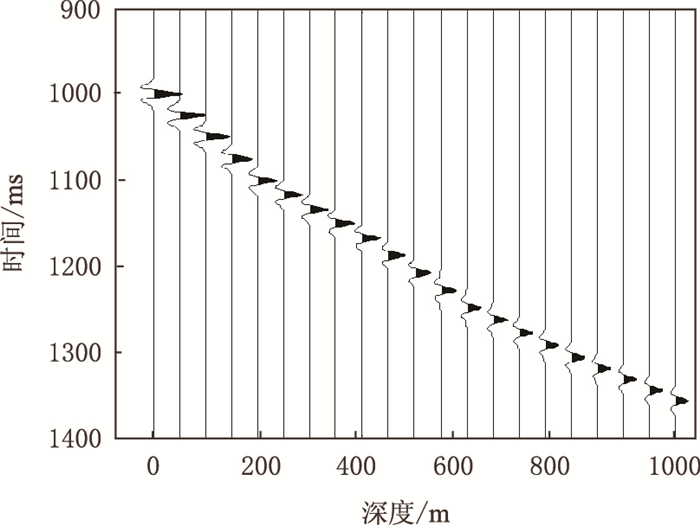 |
| 图4 正演下行波场 Fig. 4 Attenuation of wavelet |
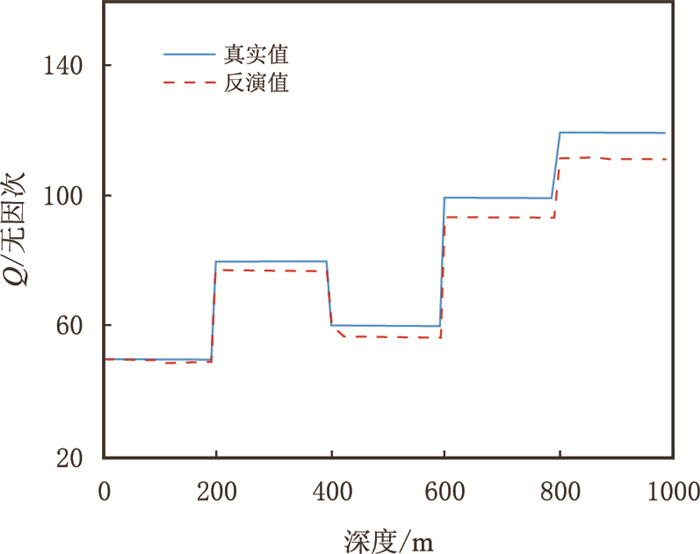 |
| 图5 Q值曲线 Fig. 5 Curve of Q value |
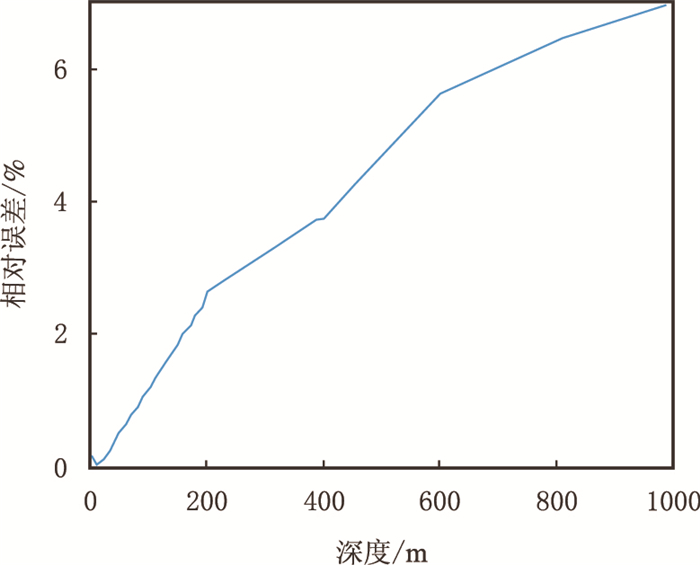 |
| 图6 相对误差 Fig. 6 The relative error |
| 表2 地层参数表 Table 2 Stratum parameters |
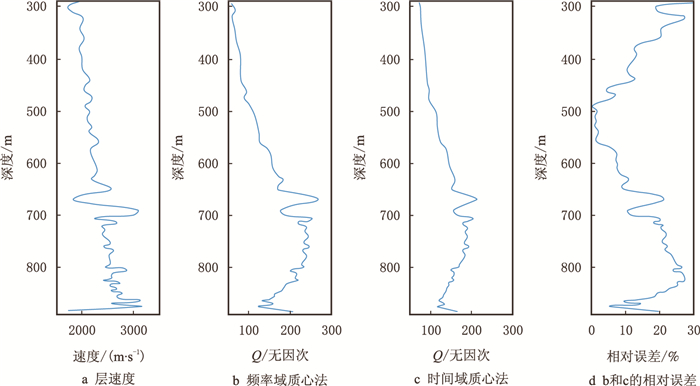
图 7是海上一VSP下行波资料,共80道记录,起始深度290 m,最深890 m,前40道检距为10 m,后40道检距为5 m,1 ms采样。利用该下行初至波场,在时间域提取各道初至波的质心频率和谱半径,分别见图 8a和图 8b,由于实际资料处理中质心和谱半径曲线难免出现振荡现象,这里对局部振荡进行了拟合平滑处理。图 9是最终反演的层介质参数,图 9a是层速度曲线,分布在2 000~3 200 m/s;图 9b是频率域质心法(即常规方法)估算的Q值曲线,分布在50~250;图 9c是时间域质心法估算的Q值曲线,分布在50~200。对比频率域和时间域质心法,两者提取的Q值存在一定的差异,图 9d为两者的相对差值百分比(以图 9b的Q值为标准),相对误差分布在0~25%,这与时间域质心法本身存在一定的理论误差以及质心、谱半径实际估算误差有关;但同时,两条Q值曲线的走向趋势基本保持一致,较好地反映了地层Q值的相对变化,证实了时间域质心法在实际生产中的实用性。对比速度和Q值曲线发现,300~700 m的Q值与速度曲线呈较好的正相关;700~900 m的Q值走向与速度走向不一致,仔细分析原始下行波场纪录以及采用其他Q值估算方法(如谱比法等)后,认为该段Q值趋势是合理的,与速度的不一致可能与该段岩性较为特殊有关。
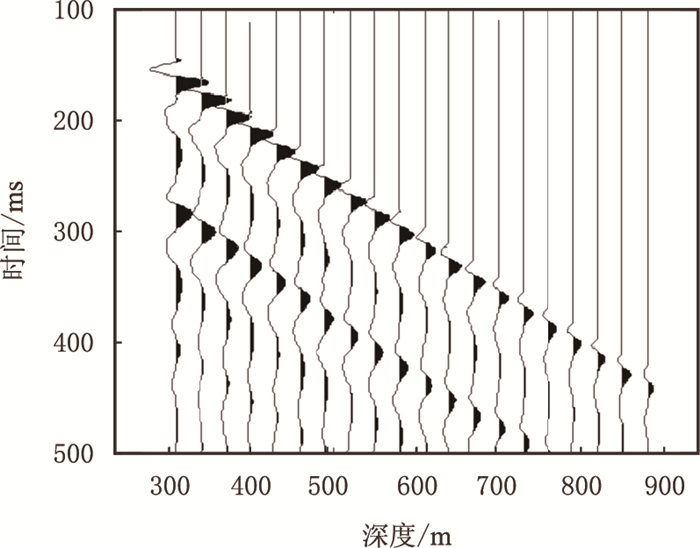 |
| 图7 VSP下行波记录 Fig. 7 VSP data |
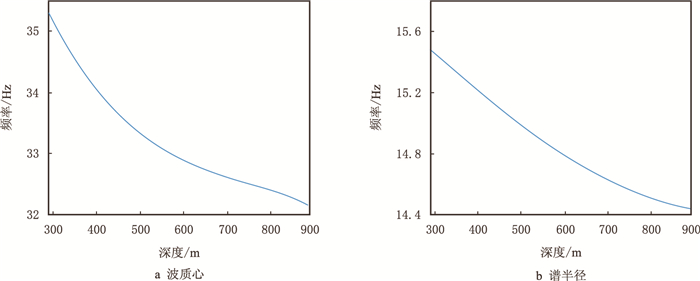 |
| 图8 各深度初至波质心及谱半径 Fig. 8 Centroid frequency and spectral radius of seismic wavelets in different depths |
 |
| 图9 Q值反演结果 Fig. 9 Q value inversion |
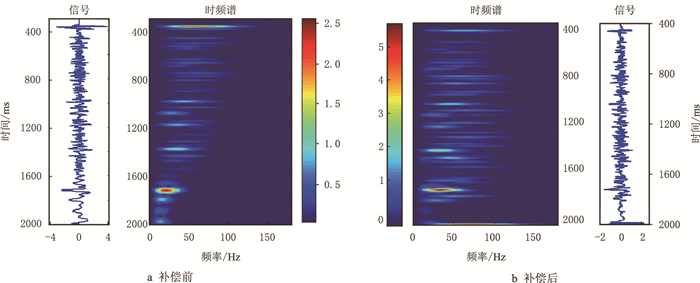
图 9显示的Q值对应的双程旅行时段约为300~900 ms,利用时间域质心法估算的该段Q值对过井剖面进行反Q补偿,深层Q取恒值120。图 10为井旁道补偿前(图 10a)、后(图 10b)的记录及其对应的时频谱,目的层为1 000~2 000 ms。从补偿前记录的时频谱上可以看到,该海上资料的浅层分辨率较高,高频可达120 Hz,随着深度的增加,主频逐渐降低,带宽变窄,能量降低。记录经补偿后,中深层的主频和带宽增加,分辨率提高,尤其是800~1 400 ms的记录,同时浅中深层的能量分布较为均衡,一致性增强。
 |
| 图10 井旁道补偿前、后的记录及其时频谱 Fig. 10 Signal and its time-frequency spectrum before and after inverse Q filtering |
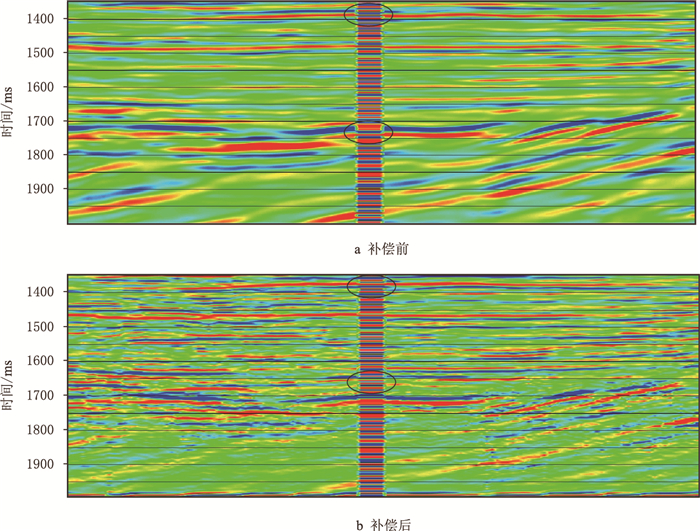
图 11是补偿前(图 11a)、后(图 11b)的过井剖面对比(1 300~2 000 ms),剖面中嵌入了井上VSP走廊叠加道进行井震对比。可以看到,补偿前剖面的分辨率较低,井震匹配度低;补偿后剖面的分辨率提高,各层能量得到合理抬升,相位得到校正,井井震匹配度增强。对比1 710 ms处的同相轴(见黑框),补偿前井旁道与走廊叠加道极性相反,补偿后两者的一致性增强,横向连续性得到改善。类似的对比还出现在1 380 ms处(见黑框),补偿后的井震匹配度得到显著改善,从侧面验证了Q值估算的合理性和可靠性。
 |
| 图11 补偿前、后记录的井震匹配 Fig. 11 Well-seismic matching before and after Q compensation |
(1) 时间域质心法规避了初至波谱的提取问题,根据子波包络提取峰值处的瞬时频率和包络宽度,再换算成质心法需要的质心频率和谱半径,实现时间域估算Q值的目的。
(2) 与常规质心法相比,时间域质心法可能更依赖于地震子波谱的假设条件(主要是时频窗面积这一因素),这是该方法的不足之处。一般地,地震子波在传播过程中其时频窗面积是变化的,将影响谱半径的准确估计,但对整体Q值趋势走向影响较小。在实际资料的处理过程中,质心频率的估算是很重要的环节,有限的波动将对Q值估算造成较大的影响。
| [1] |
马昭军, 刘洋. 地震波衰减反演研究综述[J].
地球物理学进展, 2005, 10 (4) : 1074 –1082.
Ma Zhaojun, Liu Yang. A summary of research on seismic attenuation[J]. Progress in Geophys., 2005, 10 (4) : 1074 –1082. |
| [2] |
宫同举, 孙成禹, 彭洪超, 等. 几种提取品质因子方法的对比分析[J].
勘探地球物理进展, 2009, 32 (4) : 252 –256.
Gong Tongju, Sun Chengyu, Peng Hongchao, et al. Comparison of several computational methods of quality factor[J]. Progress in Exploration Geophysics, 2009, 32 (4) : 252 –256. |
| [3] |
云美厚, 聂岩, 李运肖, 等. 地层品质因子的几种定义及相互关系[J].
石油地球物理勘探, 2013, 48 (5) : 816 –823.
Yun Meihou, Nie Yan, LiYunxiao, et al. Definition and mutual relationship of several quality factors[J]. Oil Geophysical Prospecting, 2013, 48 (5) : 816 –823. |
| [4] | Kjartansson E. Constant Q-wave propagation and attenuation[J]. J. Geophys. Res., 1979, 84 : 4737 –4748. DOI:10.1029/JB084iB09p04737 |
| [5] | Engelhard L. Determination of seismic-wave attenuation by complex trace analysis[J]. Geophysical Journal International, 1996, 125 (2) : 608 –622. DOI:10.1111/gji.1996.125.issue-2 |
| [6] | Quan Y L, Harris J M. Seismic attenuation tomography using the frequency shift method[J]. Geophysics, 1997, 62 (3) : 895 –905. DOI:10.1190/1.1444197 |
| [7] | Tu Ning, Lu Wenkai. Improve Q estimates with spectrum correction based on seismic wavelet estimation[J]. Applied Geophysics, 2010, 7 (3) : 217 –228. DOI:10.1007/s11770-010-0252-2 |
| [8] | James R. Integrated estimation of interval-attenuation profiles[J]. Geophysics, 2006, 71 (4) : 19 –23. DOI:10.1190/1.2209722 |
| [9] | Rainer T. The determination of the seismic quality factor Q from VSP data:A comparison of different computational methods[J]. Geophysical Prospecting, 1991, 39 (1) : 1 –27. DOI:10.1111/gpr.1991.39.issue-1 |
| [10] | Zhang Changjun, Ulrych T J. Estimation of quality factors from CMP records[J]. Geophysics, 2002, 67 (5) : 1542 –1547. DOI:10.1190/1.1512799 |
| [11] |
高静怀, 杨森林. 利用零偏移VSP资料估计介质品质因子方法研究[J].
地球物理学报, 2007, 50 (4) : 1198 –1209.
Gao Jinghuai, Yang Senlin. On the method of quality factors estimation from zero-offset VSP data[J]. Chinese Journal of Geophysics, 2007, 50 (4) : 1198 –1209. |
| [12] |
高静怀, 杨森林, 王大兴. 利用VSP资料直达波的包络峰值处瞬时频率提取介质品质因子[J].
地球物理学报, 2008, 51 (3) : 853 –861.
Gao Jinghuai, Yang Senlin, Wang Daxing. Quality factor extraction using instantaneous frequency at envelope peak of direct waves of VSP data[J]. Chinese Journal of Geophysics, 2008, 51 (3) : 853 –861. |
| [13] |
朱定, 陈国俊, 蔡成国. 利用VSP直达波资料反演粘弹介质的相速度及品质因子[J].
勘探地球物理进展, 2004, 27 (5) : 337 –342.
Zhu Ding, Chen Guojun, Cai Chengguo. Inversion of phase velocity and quality factor from direct waves in vertical seismic profile data[J]. Progress in Exploration Geophysics, 2004, 27 (5) : 337 –342. |
| [14] |
刘国昌, 陈小宏, 杜婧, 等. 基于整形正则化和S变换的Q值估计方法[J].
石油地球物理勘探, 2011, 46 (3) : 417 –422.
Liu Guochang, Chen Xiaohong, Du Jing, et al. Seismic Q estimation using S-transform with regularized inversion[J]. Oil Geophysical Prospecting, 2011, 46 (3) : 417 –422. |
| [15] | Reine C, Van der Baan M, Roger C. The robustness of seismic attenuation measurements using fixed and variable-window time-frequency transforms[J]. Geophysics, 2009, 74 (2) : WA123 –WA135. DOI:10.1190/1.3043726 |
| [16] | Sams M, Goldberg D. The validity of the Q estimation from borehole data using spectral ratios[J]. Geophysics, 1990, 55 (1) : 97 –101. DOI:10.1190/1.1442776 |
| [17] | Dasgupta R, Roger A, Clark. Estimation the Q from surface seismic reflection data[J]. Geophysics, 1998, 63 (6) : 2120 –2128. DOI:10.1190/1.1444505 |
| [18] | Wang Y H. A stable and efficient approach of inverse Q filtering[J]. Geophysics, 2002, 67 (2) : 657 –663. DOI:10.1190/1.1468627 |
| [19] |
李宏兵, 赵文智, 曹宏, 等. 小波尺度域含气储层地震波衰减特征[J].
地球物理学报, 2004, 47 (5) : 893 –899.
Li Hongbing, Zhao Wenzhi, Cao Hong, et al. Characteristics of seismic attenuation of gas reservoirs in wavelet domain[J]. Chinese Journal of Geophysics, 2004, 47 (5) : 893 –899. |
| [20] | Hongbing Li. Measures of scale based on the wavelet scalogram with applications to seismic attenuation[J]. Geophysics, 2006, 71 (5) : V111 –V118. DOI:10.1190/1.2211529 |
| [21] |
武银婷, 朱光明, 刘伊克, 等. 零偏VSP反演Q值CFS方法及影响因素研究[J].
地球物理学进展, 2010, 25 (6) : 1897 –1904.
Wu Yinting, Zhu Guangming, Liu Yike, et al. Study on CFS method in Q inversion using zero-offset VSP data[J]. Progress in Geophysics, 2010, 25 (6) : 1897 –1904. |
| [22] |
张大伟, 孙赞东, 王学军, 等. 利用零井源距VSP资料进行品质因子反演[J].
石油地球物理勘探, 2011, 46 (S1) : 47 –52.
Zhang Dawei, Sun Zandong, Wang Xuejun, et al. Qfactor inversion and calculation using zero-offset VSP data[J]. Oil Geophysical Prospecting, 2011, 46 (S1) : 47 –52. |
| [23] |
赵宁, 曹思远, 胡言防, 等. 频域统计性属性组合提取品质因子Q[J].
石油地球物理勘探, 2013, 48 (4) : 545 –552.
Zhao Ning, Cao Siyuan, Hu Yanfang, et al. Seismic Q estimation by combinations of frequency statistics attributes[J]. Oil Geophysical Prospecting, 2013, 48 (4) : 545 –552. |
| [24] | Barnes A E. Instantaneous spectral bandwidth and dominant frequency with applications to seismic reflection data[J]. Geophysics, 1993, 58 (3) : 419 –428. DOI:10.1190/1.1443425 |
 2014, Vol. 36
2014, Vol. 36

