电潜泵同井采注水是一种适用于边缘、零散小区块油田的注水方式,可有效解决常规注水工艺中存在的地面设施建设周期长、成本高等问题[1]。在同井采注水中,水中所含的细砂粒常会导致叶轮出现严重的冲蚀磨损,引起泵效下降,影响设备正常运行[2]。因此有必要对叶轮进行磨损分析,研究磨损机理,以便于采取相应的防护措施。
CFD数值模拟方法用于流场分析和冲蚀磨损,可有效降低成本[3-9]。本文以同井采注水中使用的电潜泵叶轮为研究对象,分析不同工况条件下内部的磨损,并进行验证。
1 离散相(颗粒)的控制方程离散相模型的基本假设是,考虑流体通过推动和涡旋对颗粒运动产生影响,忽略颗粒对流体的影响。颗粒运动轨迹的计算是独立的,被安排于流体相计算中指定的间隙中完成[10-11]。
离散相颗粒的轨道模型对拉格朗日坐标系下的颗粒作用力微分方程来求解[12-13]。颗粒运动的微分方程如下
| $ \frac{{{\rm{d}}{u_{\rm{p}}}}}{{{\rm{d}}t}} = {F_{\rm{D}}}\left( {u-{u_{\rm{p}}}} \right) + \frac{{{\rm{g}}\left( {{\rho _{\rm{p}}}-\rho } \right)}}{{{\rho _{\rm{p}}}}} + F $ | (1) |
| $ {F_{\rm{D}}} = \frac{{18L}}{{{\rho _{\rm{p}}}{d^2}}} \cdot \frac{{{C_{\rm{D}}}Re}}{{24}} $ | (2) |
式中:up—颗粒的速度,m/s;
t—时间,s;
u—流体的速度,m/s;
FD(u-up)—颗粒的单位质量曳力,N;
L—流体的动力黏度,Pa·s;
CD—曳力系数;
d—颗粒直径,mm;
ρp—颗粒的密度,kg/m3;
ρ—流体的密度,kg/m3;
F—参考坐标系的旋转引起的作用力,N,包括Basset力、Saffman升力、Magnus升力等作用力;
Re—颗粒雷诺数。
2 计算方法 2.1 计算模型的建立及网格划分所研究的叶轮为电潜泵叶轮,叶片数为7,入口位于下端,出口位于周围。使用Solidworks创建叶轮的计算域模型,使用gambit对计算域进行网格划分,得到图 1所示的非结构化网格,其中网格的最大尺寸为1 mm,总网格数约为194 672。
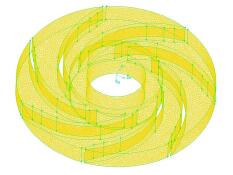 |
| 图1 网格划分 Fig. 1 Mesh |
RNG k−ε模型是对N-S方程用重组化群推导出来的湍流模型,适合于高应变率及流线弯曲较大的流动[14-23]。本文选用RNG k−ε模型对叶轮的内流特性及冲蚀磨损进行计算。
采用SIMPLE算法对压力和速度进行耦合。采用一阶迎风格式对动量方程、湍动能和湍动耗散率输运方程进行离散。
2.3 边界条件的设置(1) 入口边界条件:按速度入口设定,湍动能强度设为4.752%,水力直径设为3.845 mm。
(2) 壁面边界条件:设置为运动壁面,根据所在工况下的转速,换算出旋转角速度。
(3) 出口边界条件:按压力出口设定,湍动能强度为5%,水力直径设为11.67 mm,根据所在工况,换算出压力值。
2.4 计算中的泵工况、流体和固体颗粒的物性计算中所使用的电潜泵工况、流体物性参数如表 1所示。
| 表1 电潜泵工况及流体物性参数 Table 1 The ESP operating conditions and fluid properties |
磨损率E为边壁单位时间、单位面积下的质量损失量,最大磨损率Emax为冲蚀磨损中磨损率最高的值,用于衡量冲蚀磨损的强度。
在排量Q=120 m3/d、含砂浓度c=0.3%、叶轮转速n=3 500 r/min的条件下,对不同砂粒粒径下叶轮冲蚀磨损进行数值模拟,得到砂粒粒径与最大冲蚀磨损率的关系如图 2所示。
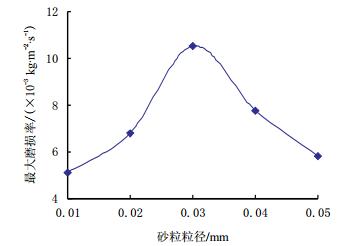 |
| 图2 含砂体积浓度一定,不同粒径条件下叶轮的最大冲蚀磨损率 Fig. 2 The maximum erosion rate of the impeller under different diameters at constant sand volume |
从图 2可看出,在排量、含砂浓度、叶轮转速等条件一定的前提下,随着砂粒粒径的增大,最大冲蚀磨损率先增加后减小,这是因为在浓度不变的前提下,砂粒粒径增大会使单位时间内流经叶轮砂粒个数减少,从而使砂粒与叶轮发生碰撞的次数减少,降低发生冲蚀磨损的机率。因此,单位时间内流经叶轮的砂粒数量是研究砂粒粒径对冲蚀磨损影响时必须要考虑的因素。
3.2 单位时间内流过砂粒个数一定,粒径对磨损的影响在排量Q=120 m3/d、每秒流经的砂粒个数为7.96~1011个、叶轮转速n=2 500 r/min情况下,对不同粒径下的冲蚀磨损进行数值模拟,得到砂粒粒径不同的情况下砂粒粒径与最大冲蚀磨损率的关系如图 3所示。
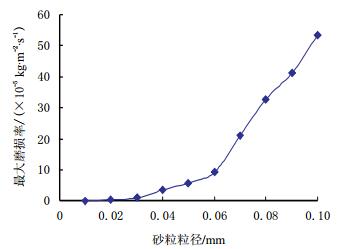 |
| 图3 单位时间内通过的砂粒数量一定,不同大小粒径下叶轮的最大冲蚀磨损率 Fig. 3 The maximum erosion rate of the impeller under the different diameter when number of sand through the flow area per second remains |
由图 3可知,当砂粒粒径在0.03 mm以下时,最大冲蚀磨损率较小;在0.03~0.07 mm时,最大磨损率开始上升;当砂粒粒径超过0.07 mm时,最大冲蚀磨损率急剧上升且上升速率加快。由此可见,粒径超过0.07 mm的砂粒对叶轮的冲蚀破坏极大,对设备的安全运行产生了极其严重的威胁,易造成严重的破坏失效,应该采取有效方案加以防范。
单位时间内流经的砂粒个数相同,砂粒粒径增大,含砂浓度也增大。因此,含砂浓度的增大会加剧冲蚀磨损程度。
3.3 浓度、排量、粒径一定,转速对最大磨损率Emax的影响选取含砂浓度c=0.3%、砂粒粒径d=0.10 mm、转速分别为2 900,2 700,2 500,2 300 r/min几个工况,对叶轮的冲蚀磨损进行数值模拟,得到冲蚀磨损区域以及最大冲蚀磨损率。
根据公式
| $ {\rm{Q}} = Q'\frac{{\rm{n}}}{{n'}} $ | (3) |
式中:
Q—额定转速下的排量,m3/d,取50 m3/d;
Q'—实际运行时的排量,m3/d;
n—额定转速,r/min,取2 900 r/min;
n'—实际运行时的转速,r/min。
可知,转速2 300,2 500,2 700,2 900 r/min对应的排量分别是39.66,43.10,46.55,50.00 m3/d。
图 4是不同转速条件下的叶轮冲蚀磨损区域分布。图中可以看出,叶轮较严重的冲蚀磨损区域位于凹面,该面临近叶片中心处磨损较严重,随着转速的增大,磨损严重的区域逐渐扩大,当转速n=2 900 r/min时,磨损严重的范围扩展到整个叶片凹面;而叶片凸面、叶轮上下盖板磨损较弱。
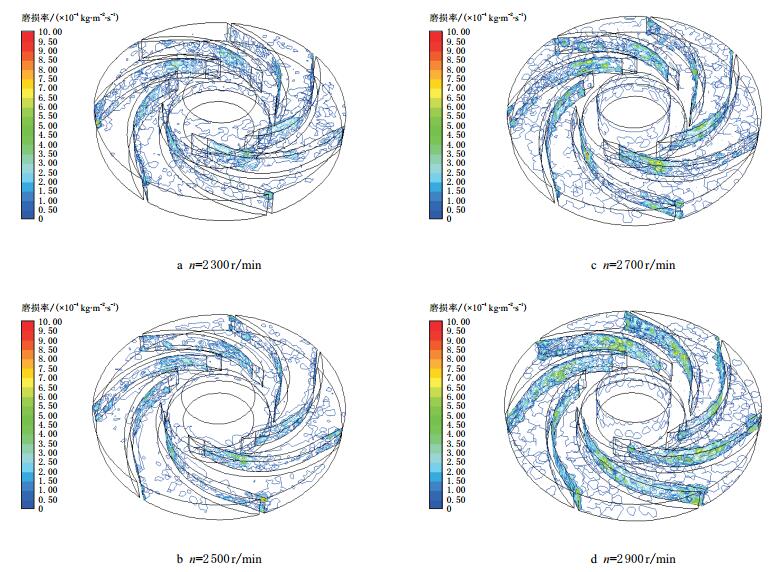 |
| 图4 不同转速条件下的叶轮磨损区域 Fig. 4 The erosion area under different speed conditions |
图 5是不同转速条件下,叶轮的最大冲蚀磨损情况,可以看出,转速的增大会加剧叶轮的冲蚀磨损。因此,在满足泵效、扬程等要求的前提下,适当减小转速,可实现降低冲蚀磨损的效果。如,当转速由2 900 r/min降至2 700 r/min时,最大冲蚀磨损率会从8.91×10-4 kg/(m2·s)降低到8.03×10-4 kg/(m2·s),降低10.91%。
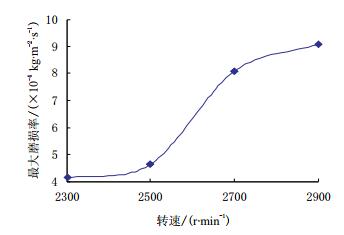 |
| 图5 不同转速条件下,叶轮的最大冲蚀磨损率 Fig. 5 The maximum erosion rate under different speed conditions |
为验证数值模拟得出的叶轮主要磨损区域,采用三坐标测量机对过流部件进行了磨损区域检测。
三坐标精密检测技术是以精密机械为基础综合应用光学、电子技术、传感技术、计算机技术等多项先进技术组成的测量仪器,能完成几何尺寸、形状与位置公差的测量,测量精度可达0.1 μm。图 6为叶轮磨损区域检测。
 |
| 图6 叶轮磨损区域检测 Fig. 6 The detection of impeller wear area |
测量时将被测物体置于三坐标测量机的测量空间,可获得被测物体上各测量点的坐标值,根据这些点的空间坐标值经过数学运算求出被测物体的几何尺寸,形状公差。
测试前,将叶轮沿轴截面切开,设置其轴线方向为y,选择一些点,其x和z方向的坐标及其PROFP值进行检测,测得其理论值、实际值和误差值。PROFP为轮廓度,是形位公差的一种,表示实际轮廓点与理论点位置的差异,其误差值表示磨损程度,误差值越大,磨损越严重。
测试时,采用即点即测的方式在叶片曲面上打点,形成9个点(图 7),并将这些点的位置与理论轮廓点的位置做比对,最终可以得到检测各点的PROFP值(表 2)。
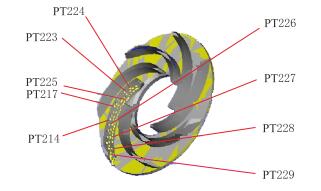 |
| 图7 检测点 Fig. 7 Detection point |
| 表2 检测报告 Table 2 The examining report |
根据检测报告可知,从流道入口至出口的9个点PT224、PT223、PT225、PT217、PT214、PT226、PT227、PT228、PT229的PROFP误差值分别为-0.122 4,-0.148 8,-0.267 6,-0.320 2,-0.378 2,-0.407 3,-0.331 5,-0.249 9,-0.203 9 mm。磨损最严重的位置在叶片凹面的中部,接近入口和出口磨损量逐渐降低,这一趋势与上一小节数值模拟得到的主要磨损区域相同,验证了数值模拟的正确性。
5 结论(1) 数值模拟结果与检测结果基本符合,数值模拟方法可靠,可在一定程度上取代现场试验。
(2) 0.07 mm是叶轮冲蚀磨损的临界值,砂粒粒径超过0.07 mm,冲蚀磨损将迅速加剧。采用有效方法对粒径超过0.07 mm的砂粒进行分离,可有效降低冲蚀磨损。
(3) 叶轮的冲蚀磨损主要产生于叶片凹面内侧,中间处最严重,而在凸面和下盖板只存在较小的冲蚀磨损,在叶片凹面增加防护涂层,可达到降低冲蚀磨损的效果。
| [1] |
邱永发, 罗代亮, 谢卫兵, 等. 电潜泵同井采注水工艺及关键技术研究[J].
石油机械, 2013, 41 (7) : 102 –106.
Qiu Yongfa, Luo Dailiang, Xie Weibing, et al. ESP one-well recovery and waterflooding technology and key techniques[J]. China Petroleum Machinery, 2013, 41 (7) : 102 –106. |
| [2] |
王尊策, 陈思, 李森, 等. 基于CFD的潜油电泵叶轮冲刷磨损数值模拟[J].
石油矿场机械, 2013, 42 (5) : 31 –34.
Wang Zunce, Chen Si, Li Sen, et al. Numerical simulation of particle impact erosion within electric submersible pump based on CFD[J]. Oil Field Equipment, 2013, 42 (5) : 31 –34. |
| [3] |
邵德艳, 周丽清. 断块油藏注水见效类型研究[J].
西南石油大学学报, 2007, 29 (5) : 30 –33.
Shao Deyan, Zhou Liqing. Water flooding effect in block reservoirs[J]. Journal of Southwest Petroleum University, 2007, 29 (5) : 30 –33. |
| [4] |
胡坤, 彭旭, 李杰, 等. 基于CFD的自推进破岩喷嘴流场仿真研究[J].
西南石油大学学报:自然科学版, 2013, 35 (6) : 159 –165.
Hu Kun, Peng Xu, Li Jie, et al. Simulation based on the CFD of self-propulsion Nozzle's flow field[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2013, 35 (6) : 159 –165. |
| [5] | Jackon R. Locally averaged equations of motion for a mixture of identical spherical particles and a newtonian fluid[J]. Chemical Engineering Science, 1997, 52 (15) : 2457 –2469. DOI:10.1016/S0009-2509(97)00065-1 |
| [6] |
刘波, 吴海, 何红阳, 等. 基于CFD的锥直喷嘴的过渡圆弧优化分析[J].
液压气动与密封, 2011 (6) : 36 –38.
Liu Bo, Wu Hai, He Hongyang, et al. Simulation of tapered spray gun's infulence on two phase flow with fluent[J]. Hydraulics Pneumatics & Seals, 2011 (6) : 36 –38. |
| [7] |
万里平, 何保生, 唐洪明, 等. 冲砂洗井泡沫携砂规律数值模拟研究[J].
西南石油大学学报:自然科学版, 2013, 35 (4) : 101 –106.
Wan Liping, He Baosheng, Tang Hongming, et al. Numerical simulation on sand carrying rule of sand washing and flushing foam fluid[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2013, 35 (4) : 101 –106. |
| [8] |
练章华, 陈新海, 林铁军, 等. 排砂管线弯接头的冲蚀机理研究[J].
西南石油大学学报:自然科学版, 2014, 36 (1) : 150 –156.
Lian Zhanghua, Chen Xinhai, Lin Tiejun, et al. Study on erosion mechanism of bending joint in blooey line[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2014, 36 (1) : 150 –156. |
| [9] |
梁政, 任连城, 张梁, 等. 水力旋流器流场径向速度分布规律研究[J].
西南石油大学学报:自然科学版, 2007, 29 (1) : 106 –108.
Liang Zheng, Ren Liancheng, Zhang Liang, et al. The distribution law of radial velocity of flow field in hydrocyclone[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2007, 29 (1) : 106 –108. |
| [10] |
黄思, 王朋, 区国惟, 等. 多级多出口离心泵的数值模拟及试验验证[J].
流体机械, 2013, 41 (1) : 10 –13.
Huang Si, Wang Peng, Ou Guowei, et al. Numerical simulation and experimental verification of multistage and multioutlet centrifugal pump[J]. Fluid Machinery, 2013, 41 (1) : 10 –13. |
| [11] |
潘海波, 郭宏伟, 虞维平, 等. 离心除尘风机气固两相流动的数值模拟[J].
流体机械, 2005, 33 (6) : 11 –13.
Pan Haibo, Guo Hongwei, Yu Weiping, et al. Simulation of the gas-particle turbulent flow of centrifugal fan[J]. Fluid Machinery, 2005, 33 (6) : 11 –13. |
| [12] |
杨敏官, 刘栋, 康灿, 等. 离心泵叶轮内部伴有盐析流场的分析[J].
农业机械学报, 2006, 37 (12) : 83 –86.
Yang Minguan, Liu Dong, Kang Can, et al. Analysis of flow with salt's separation and accumulation in centrifugal pump impeller[J]. Journal of Agricultural Machinery, 2006, 37 (12) : 83 –86. |
| [13] |
闫顺林, 魏杰儒, 李燕芳, 等. 基于离散相模型的旋转煤粉分离器流场数值研究[J].
应用能源技术, 2012 (8) : 15 –17.
Yan Shunlin, Wei Jieru, Li Yanfang, et al. Numerical study for fluid field in rotating pulverizedoal classifier based on the discrete phase model[J]. Applied Energy Technology, 2012 (8) : 15 –17. |
| [14] |
王巧燕, 唐安江, 蒋东海, 等. 黄磷喷淋塔数值模拟研究[J].
流体机械, 2013, 41 (2) : 78 –82, 77.
Wang Qiaoyan, Tang Anjiang, Jiang Donghai, et al. Numerical simulation of open spay tower for phosphorus production[J]. Fluid Machinery, 2013, 41 (2) : 78 –82, 77. |
| [15] |
赵新学, 金有海, 孟玉青, 等. 旋风分离器壁面磨损的数值分析[J].
流体机械, 2010, 38 (4) : 18 –22.
Zhao Xinxue, Jin Youhai, Meng Yuqing, et al. Numerical analysis on the erosion of cyclone separator's surface wall[J]. Fluid Machinery, 2010, 38 (4) : 18 –22. |
| [16] |
冯俊, 郑源. 基于CFD的轴流泵三维湍流数值模拟[J].
流体机械, 2012, 40 (11) : 33 –36.
Feng Jun, Zheng Yuan. Three-dimensional viscous numerical simulation of axial-flow pump based on CFD[J]. Fluid Machinery, 2012, 40 (11) : 33 –36. |
| [17] | Speziable C G, Thangam S. Analysis of an RNG based turbulence model for separated flows[J]. International Journal Engineering Science, 1992, 30 (10) : 1379 –1388. DOI:10.1016/0020-7225(92)90148-A |
| [18] |
刘苏, 苏庆伟, 黄坤, 等. 仰角式油水分离器流场的数值模拟[J].
西南石油大学学报:自然科学版, 2012, 34 (6) : 147 –152.
Liu Su, Su Qingwei, Huang Kun, et al. Numerical simulation of flow field of the inclined oil-water separator[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2012, 34 (6) : 147 –152. |
| [19] | Malhotra A, Branion R M R, Hauptmann E G. Modelling the flow in a hydrocyclone[J]. The Canadi Journal of Chemical Engineering, 1994, 72 (1) : 953 –960. |
| [20] |
任芸, 刘厚林, 舒敏骅, 等. 湍流模型在离心泵偏工况性能预测中的适用性分析[J].
流体机械, 2012, 40 (10) : 18 –22.
Ren Yun, Liu Houlin, Shu Minhua, et al. Analysis of applicability of turbulence models in performance prediction for centrifugal pumps at the off-design conditions[J]. Fluid Machinery, 2012, 40 (10) : 18 –22. |
| [21] |
艾志久, 蒋静, 吴昌, 等. 炉内燃烧场数值模拟研究[J].
西南石油大学学报:自然科学版, 2011, 33 (3) : 165 –168.
Ai Zhijiu, Jiang Jing, Wu Chang, et al. Study on the numerical simulation of the combustion in the burning furnace[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2011, 33 (3) : 165 –168. |
| [22] |
李丹, 马贵阳, 杜明俊, 等. 基于离散相模型的旋风分离器内部流场数值研究[J].
流体机械, 2011, 39 (9) : 21 –25.
Li Dan, Ma Guiyang, Du Mingjun, et al. Numerical study for flow field in a cyclone separator[J]. Fluid Machinery, 2011, 39 (9) : 21 –25. |
| [23] |
王常斌, 卜娉婷, 支树洁. 基于PHOENICS的喷射泵最佳喉嘴距数值模拟[J].
大庆石油学院学报, 2009, 33 (1) : 41 –44.
Wang Changbin, Bu Pinting, Zhi Shujie. Numerical simulation of the best throat pipe diameter of jet pump based on PHOENICS[J]. Journal of Daqing Petroleum Institute, 2009, 33 (1) : 41 –44. |
 2014, Vol. 36
2014, Vol. 36

