2. 中国石油西部管道公司乌鲁木齐输油气分公司, 新疆 乌鲁木齐 830000;
3. 中国石油西南管道公司兰成渝输油分公司, 四川 成都 610069
2. Urumqi Oil and Gas Branch Company, Western Pipeline Company, PetroChina, Urumqi, Xinjiang 830000, China;
3. Lan-Cheng-Yu Oil Transportion Branch Company, Western Pipeline Company, PetroChina, Chengdu, Sichuan 610069, China
X52管线钢是油气储运中常用的管道材料,具有良好的力学性能和工艺性能。由于管道运输近年来才日趋普遍,而X52管线钢多用于管道油气储运领域,国内对该钢材力学性能方面的研究相对较少,可供分析的实验数据不充分,其理论计算和设计方法也不完备。研究X52管线钢的力学性能指标发现,X52管线钢进入塑性状态后,其应力-应变曲线表现为典型的非线性,没有明显的屈服平台。应变不仅与应力状态有关,还与变形的历史有关。为了考虑变形历史,需要研究应力和应变增量之间的关系,以这种关系为基础的理论称为增量理论[1]。在比例变形条件下,通过对增量理论的应力和应变增量关系的积分可得到全量理论的应力-应变关系。
长期以来,基于应力的判据处于主导地位。然而,随着研究的深入和发展,越来越多的研究表明,在某些特殊工况环境下,如冻土、地震和滑坡等地质灾害区域的地表位移影响下,管道承受的应力虽然已经达到或超过应力判别准则的要求,但是管道还能够满足输送要求,这种情况下基于应力的判据就显得过于保守,由此,产生了所谓的基于应变的管道失效判据,即认为管道的失效不再由应力控制,而是由应变控制。
此外,精确描述X52管线钢的应力-应变关系、建立其失效判据也是管道结构受力及稳定性分析等相关研究工作的基础。
1 X52管线钢的理论本构关系与修正在万能材料实验机上,选取10件X52钢材标准试件进行拉伸实验,实验应力-应变曲线见图 1a。选取一典型的曲线作为此钢材试样本构关系修正的计算依据(图 1b),其力学特征参数见参考文献[2]。
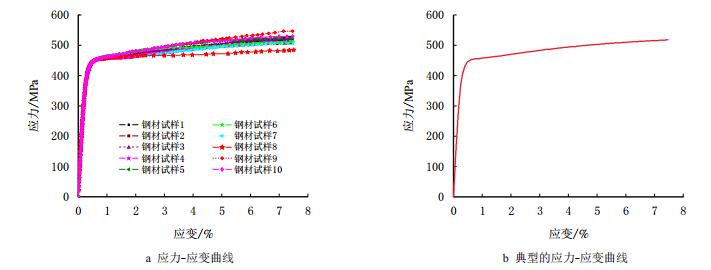 |
| 图1 X52管线钢的拉伸实验应力-应变曲线 Fig. 1 Stress-strain curves of X52 pipeline steel in tensile test |
根据X52(L360)管线钢的实验本构关系曲线,提出全局二段式管线钢应力-应变模型。第一阶段为应力在条件屈服极限范围内,即ε≤εP0.2时,采用传统的Ramberg-Osgood本构模型来表示单轴非线性应力-应变关系,此模型视总应变为弹性应变和塑性应变之和
| $ {\varepsilon _{总}} = {\varepsilon _{\rm{e}}} + {\varepsilon _{\rm{P}}} = \frac{\sigma }{{{E_0}}} + {\left( {\frac{\sigma }{K}} \right)^n} $ | (1) |
令
| $ {K^n} = \frac{{\sigma _{\rm{s}}^n}}{{{\varepsilon _0}\frac{\sigma }{{{\sigma _{\rm{s}}}}}\frac{r}{{n + 1}}}} $ | (2) |
由
| $ {\varepsilon _{总}} = \frac{\sigma }{{{E_0}}}\left[{1 + \frac{r}{{n + 1}}{{\left( {\frac{\sigma }{{{\sigma _{\rm{s}}}}}} \right)}^n}} \right] $ | (3) |
对于X52(L360),n=10,r=9,根据文献[2],X52(L360)管线钢力学特征技术规格书的要求,σs=360 Mpa,其本构关系方程可表述为[3]
| $ \varepsilon = \frac{\sigma }{{{E_0}}}\left[{1 + \frac{9}{{11}}{{\left( {\frac{\sigma }{{360}}} \right)}^{10}}} \right] $ | (4) |
将Ramberg-Osgood方程建立的本构关系曲线与X52(L360)管线钢实验本构关系曲线进行对比可见(图 2),当ε≤εP0.2时,Ramberg-Osgood本构方程能够比较准确地反映X52管线钢的应力-应变曲线,ε>εP0.2时,基于上述模型所得理论本构曲线与实验结果有较大的误差。因此对于超出εP0.2的大应变,有必要对Ramberg-Osgood模型做出修正。
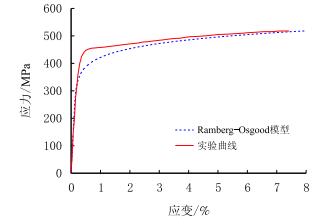 |
| 图2 X52管线钢的Ramberg-Osgood模型与试验应力-应变曲线对比图 Fig. 2 The comparison between X52 pipeline steel's Ramberg-Osgood model and experimental stress-strain curve |
由X52的实验拉伸本构关系可见:X52(L360)钢材没有明显的屈服平台,工程上常采用卸载后剩余0.2%的塑性变形所对应的应力为屈服极限。根据实验数据,提出用条件屈服极限σP1.0来代替极限应力,在σP0.2和σP0.1间采用如下表达式
| $ {\varepsilon _{{\rm{总}}}} = \frac{{\sigma-{\sigma _{{\rm{P0}}.{\rm{2}}}}}}{{{E_{0.2}}}} + R{\left( {\frac{{\sigma-{\sigma _{{\rm{P}}0.2}}}}{{{\sigma _{{\rm{P}}1.0}}-{\sigma _{{\rm{P}}0.2}}}}} \right)^{{n_{0.2, 1.0}}}} + {\varepsilon _{{\rm{P}}0.2}} $ | (5) |
| $ R = 0.008 + \left( {{\sigma _{{\rm{P}}1.0}}-{\sigma _{{\rm{P}}0.2}}} \right)\left( {\frac{1}{{{E_0}}}-\frac{1}{{{E_{0.2}}}}} \right) $ | (6) |
n0.2, 1.0 值可根据模型与实验所得应力-应变曲线的符合程度求出,εP0.2=0.2% + ε0。
综合上述分析,全局二段式管线钢应力-应变关系可表达为:当σ≤σP0.2时,采用式(3),当σP0.2 < σ≤σP1.0时,采用式(5)。
由实验曲线可见(图 2),σP0.2=410.00 MPa,σP1.0=455.43 MPa;又:
| $ {n_{0.2, 1.0}} = 12.255\left( {\frac{{{E_{0.2}}}}{{{E_0}}}} \right)\left( {\frac{{{\sigma _{{\rm{P1}}.{\rm{0}}}}}}{{{\sigma _{{\rm{P0}}.{\rm{2}}}}}}} \right) + 1.037 = 2.27 $ | (7) |
具体地,当σP0.2 < σ≤σP1.0时,由式(5)可得
| $ \varepsilon = \frac{{\sigma-410}}{{18646.95}} + 0.00566{\left( {\frac{{\sigma-410}}{{45.43}}} \right)^{2.27}} + 0.0037 $ | (8) |
按照σP0.2的技术规格书要求,其数值为360~530 MPa,通过与实验曲线的拟合修正,式(8)可修正为
| $ \varepsilon = \frac{{\sigma-396}}{{16535.43}} + 0.0086{\left( {\frac{{\sigma-396}}{{45.43}}} \right)^{2.6}} + 0.0031 $ | (9) |
由图 3可见,修正后的公式也适用于σ≥σP1.0时X52管线钢的本构关系。
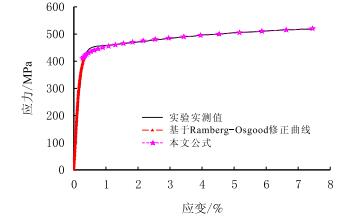 |
| 图3 X52管线钢的修正方程与实验实测结果对比 Fig. 3 The comparison between X52 pipeline steel's correction equation and experimental result |
分析X52管线钢的Ramberg-Osgood本构关系,可知r和n值越小,曲线的曲率越大,且r < n+1时,曲率增大,r > n+1时,曲率变小。任意取两组拉伸实验曲线确定的参数,如:(0.031 29,50.448 90),(0.103 54,186.020 00)代入式(3),得r=2,n=6,对比发现,此参数与实验曲线更加吻合。由此,X52(L360)管线钢材料拉伸应力应变关系可表述为
| $ \varepsilon = {\varepsilon _{\rm{e}}} + {\varepsilon _{\rm{P}}} = \frac{\sigma }{{{E_0}}}\left[ {1 + \frac{2}{7}{{\left( {\frac{\sigma }{{{\sigma _s}}}} \right)}^6}} \right]\;\;\sigma \le {\sigma _{0.2}} $ | (10) |
和
| $ \varepsilon = \frac{{\sigma-396}}{{16535.43}} + 0.0031 + 0.0086{\left( {\frac{{\sigma-396}}{{45.43}}} \right)^{2.6}}\;\;\;\sigma > {\sigma _{0.2}} $ | (11) |
依据式(10)、式(11)绘制的X52拉伸应力应变关系如图 3红色曲线所示。由图 3可见,建立的X52管线钢的拉伸应力应变关系与实验结果更加吻合,可作为该管线钢实际拉伸本构关系。
2 X52管线钢本构关系的矩阵表达大变形时X52管线钢将出现几何与材料的非线性,通常认为,几何非线性与材料非线性相关,且用矩阵方程来表达其相关函数。按照塑性理论,对于一般的各项异性材料理论上是9×9矩阵,81个参数[1]。由对称性可以缩减,对于具体的材料还能进一步缩减。一直缩减至各向同性只剩下两个参量控制,就是通常所说的拉梅常数。
在弹塑性问题中,应力全量和应变全量的关系与加载历史有关,而不是单值函数。由于强化材料在加载过程中,屈服面的大小、形状和位置发生了变化。设k为反映加载历史的强化参数矩阵,则其屈服面方程为[1]
| $ f{\rm{(}}\boldsymbol{\sigma} ,{\boldsymbol{\varepsilon} _{\rm{P}}},\boldsymbol{k}) = 0 $ | (12) |
由X52的实验拉伸本构关系可见,材料在一个方向屈服强度提高(强化),其他方向的屈服强度也同时提高,加载面均匀扩大,可视为等向强化[1]。有
| $ f\left( {{\bf{\sigma }},\boldsymbol{k}} \right) = 0 $ | (13) |
其中,强化参数矩阵k一般取塑性功或等效塑性应变,这里取等效塑性应变
| $ \boldsymbol{k} = \int {{\rm{d}}\overline {{\varepsilon _{\rm{P}}}} } $ | (14) |
加载时的本构关系,通常采用关联流动法则,即与屈服条件相关的本构关系。采用Mises模型本构矩阵,Mises屈服条件的表达式为
| $ f = \sqrt {3{I_2}}-{\sigma _{\rm{s}}} = 0 $ | (15) |
其中
由强化材料的加载条件df=0,得塑性材料的全量本构关系[5]
| $ {\boldsymbol{\sigma }} = {\boldsymbol{D}_{{\rm{ep}}}}{\boldsymbol{\varepsilon }} $ | (16) |
其中
| $ \begin{array}{l} {\boldsymbol{D}_{{\rm{ep}}}} = \boldsymbol{D} - {\boldsymbol{D}_{\rm{P}}}\\ \boldsymbol{\sigma} = {\left[{{\sigma _x}, {\sigma _y}, {\sigma _z}, {\tau _{xy}}, {\tau _{yz}}, {\tau _{zx}}} \right]^{\rm{T}}}\\ \boldsymbol{\varepsilon} = {\left[{{\varepsilon _x}, {\varepsilon _y}, {\varepsilon _z}, {\gamma _{xy}}, {\gamma _{yz}}, {\gamma _{zx}}} \right]^{\rm{T}}} \end{array} $ |
对随动强化材料,
| $ {\boldsymbol{D}} = A\left[{\begin{array}{*{20}{l}} {1-\nu }&\nu &\nu &0&0&0\\ \nu &{1-\nu }&\nu &0&0&0\\ \nu &\nu &{1-\nu }&0&0&0\\ 0&0&0&{\frac{{1 - 2\nu }}{2}}&0&0\\ 0&0&0&0&{\frac{{1 - 2\nu }}{2}}&0\\ 0&0&0&0&0&{\frac{{1 - 2\nu }}{2}} \end{array}} \right] $ |
Dp=BSST;S=[S11, S22, S33, 2S12, 2S23, 2S31];
代入式(12),即可得到X52管线钢Mises模型本构关系方程。单拉应力状态下,S11=σx;S22=0;S33=−σx;S12=S23=S31=0;E=207.00 GPa,ν=0.3;A=398.077 GPa;G=79.615 GPa;B=1689.45 GPa;由式(12),得到此时X52管线钢Mises模型本构方程
| $ \left[{\begin{array}{*{20}{l}} {{\sigma _x}}\\ {{\sigma _y}}\\ {{\sigma _z}}\\ {{\tau _{xy}}}\\ {{\tau _{yz}}}\\ {{\tau _{zx}}} \end{array}} \right] = \left[{\begin{array}{*{20}{l}} {205.67}&{119.42}&{192.40}&0&0&0\\ 0&{278.65}&{119.42}&0&0&0\\ 0&0&{205.67}&0&0&0\\ 0&0&0&{79.62}&0&0\\ 0&0&0&0&{79.62}&0\\ 0&0&0&0&0&{79.62} \end{array}} \right]\;\;\left[{\begin{array}{*{20}{l}} {{\varepsilon _x}}\\ {{\varepsilon _y}}\\ {{\varepsilon _z}}\\ {{\gamma _{xy}}}\\ {{\gamma _{yz}}}\\ {{\gamma _{zx}}} \end{array}} \right] $ | (17) |
长输管道受环境载荷影响,极易发生力学失效。如水灾掏空引起的管道大面积悬空、滑坡引起的意外冲击载荷、地震引起的地震波、铁路公路穿跨越处的交变载荷等。通常,将外部载荷引起的管道响应称为载荷控制响应,位移引起的管道结构响应称为位移控制响应。由管线钢应力-应变实验曲线可见,当应力或应变达到某一临界值时,管线钢将发生强度失效或塑性失效。根据是取应力还是取应变作为衡量管道失效时的准则,分别有基于应力的失效判据和基于应变的失效判据。下面根据X52管线钢的实验本构关系,给出确定管道失效时应力或应变临界值的力学依据和方法。
3.1 基于应力的失效准则按照文献[6]、[7]的规定,管道的强度设计遵循基于应力的失效准则。即在工作载荷条件下,管道本体可能出现的最大应力小于其屈服应力。由于仅在内压作用下,管道的周向薄膜应力为轴向薄膜应力的2倍[8],而滑坡、悬空、水冲、地震等外部载荷通常仅引起管道轴向应力的变化。故管道的强度应同时满足以下两个准则。
3.1.1 基于周向应力的强度失效准则该准则要求工况条件下管道的周向应力应小于管线钢的许用应力,即满足[2]
| $ {\sigma _{\rm{\phi}}}{\rm{< }}[{\sigma _{\rm{t}}}] = C\phi {\sigma _{\rm{s}}} $ | (18) |
其中,设计系数C反映了管道工程中的安全裕度。按照文献[7]的规定,输油管道的设计系数一般为0.72,随着高强度钢的使用和管道施工工艺的优化,文献[9]、[10]中将此范围放宽到0.8;输气管道则根据管道通过地区沿线的人口和建筑物的密集程度,划分为四个等级:一级地区为0.72,二级地区为0.6,三级地区为0.5,四级地区为0.4[6]。
3.1.2 基于组合应力条件的弹性失效准则通常管道除承受油气内压、土壤外压外,还可能存在安装载荷、地质灾害引起的意外载荷、周围环境引起的环境载荷等,管道本体除周向应力外,还存在轴向应力,对于厚壁管道,径向应力也不能忽略,即管道处于三向应力状态下。按照Lame公式,厚壁圆筒在设计条件下的三向应力表达式为[8]
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _\rm{\phi} } = \frac{{{p_{\rm{i}}}{R_{\rm{i}}}^2- {p_{\rm{o}}}{R_{\rm{o}}}^2}}{{{R_{\rm{o}}}^2- {R_{\rm{i}}}^2}} + \frac{{({p_{\rm{i}}}- {p_{\rm{o}}}){R_{\rm{i}}}^2{R_{\rm{o}}}^2}}{{{R_{\rm{o}}}^2 - {R_{\rm{i}}}^2}} \cdot \frac{1}{{{{r'}^2}}}}\\ {{\sigma _{\rm{r}}} = \frac{{{p_{\rm{i}}}{R_{\rm{i}}}^2 - {p_{\rm{o}}}{R_{\rm{o}}}^2}}{{{R_{\rm{o}}}^2 - {R_{\rm{i}}}^2}} - \frac{{({p_{\rm{i}}} - {p_{\rm{o}}}){R_{\rm{i}}}^2{R_{\rm{o}}}^2}}{{{R_{\rm{o}}}^2 - {R_{\rm{i}}}^2}} \cdot \frac{1}{{{{r'}^2}}}}\\ {{\sigma _\rm{\theta} } = \frac{{{p_{\rm{i}}}{R_{\rm{i}}}^2 -{p_{\rm{o}}}{R_{\rm{o}}}^2}}{{{R_{\rm{o}}}^2 -{R_{\rm{i}}}^2}}} \end{array}} \right. $ | (19) |
按照第三强度理论[1](最大剪应力理论),有
| $ {\tau _{\max }} = \frac{1}{2}{({\sigma _\rm{\phi} } - {\sigma _{\rm{r}}})_{r' = {R_{\rm{i}}}}} \le \frac{1}{2}[{\sigma _{\rm{t}}}] $ | (20) |
将式(19)代入式(20),得第三强度理论条件下管道的强度失效准则
| $ \frac{{2({p_{\rm{i}}}- {p_{\rm{o}}}){R_{\rm{o}}}^2}}{{{R_{\rm{o}}}^2- {R_{\rm{i}}}^2}} \le [{\sigma _{\rm{t}}}] $ | (21) |
按照第四强度理论(最大形状改变比能理论),认为最大形状改变比能达到一定值时发生屈服,屈服条件的表达式为[11]
| $ {\left. {\frac{1}{{\sqrt 2 }}\sqrt {{{\left( {{\sigma _\rm{\phi} }- {\sigma _\rm{\theta} }} \right)}^2} + {{\left( {{\sigma _\rm{\theta} }- {\sigma _{\rm{r}}}} \right)}^2} + {{\left( {{\sigma _{\rm{r}}}- {\sigma _\rm{\phi} }} \right)}^2}} } \right|_{r' = {R_{\rm{i}}}}} \le [{\sigma _{\rm{t}}}] $ | (22) |
将式(19)代入式(22),得第四强度理论条件下管道的强度失效准则
| $ \frac{{\sqrt 3 ({p_{\rm{i}}}- {p_{\rm{o}}}){R_{\rm{o}}}^2}}{{{R_{\rm{o}}}^2- {R_{\rm{i}}}^2}} \le [{\sigma _{\rm{t}}}] $ | (23) |
实验结果表明,基于周向应力和根据第三强度理论建立的X52管线钢强度失效准则过于保守,通常采用基于第四强度理论建立的管线钢强度失效准则,在此准则条件下,管道失效时的临界应力为
| $ {\sigma _{{\rm{cr}}}} = \frac{{\sqrt 3 ({p_{\rm{i}}}-{p_{\rm{o}}}){R_{\rm{o}}}^2}}{{{R_{\rm{o}}}^2-{R_{\rm{i}}}^2}} $ | (24) |
管道施工设计中,主要依据应力准则。然而,实验结果显示,X52管线钢塑性极好,其延伸率高达41%,尽管某些特殊工况下的(如悬空等)管道承受的载荷应力失效临界值已经达到或超过应力判别准则的极限,但由于管线钢极其优越的塑性,管道依然能够安全运营。如兰成渝输油管道于2010年在德阳石亭江段曾遭遇特大洪水,导致管道悬空380.0 m,按照文献[2],管道悬空48.4~m即发生失效,按照文献[12]和文献[13],计算后可以确定该处管道悬空长度超过58.6~m后即发生失效。但事实上,该处管段并未被拉断。实验和实践均表明,基于应力的强度失效准则过于保守。由此,产生了基于应变的管道失效准则,即认为管道的失效不再由应力控制,而是由应变控制。
按照空间几何分布,管道均匀变形可分为拉伸变形、压缩变形和椭圆化变形。拉伸(压缩)变形通常由内压、覆土压力、管道自重、温度应力、地质灾害等环境载荷引起。椭圆化变形则主要由外压引起。为防止过量变形引发管道失效,需要限制管道拉伸应变、压缩应变和椭圆化变形。
3.2.1 拉伸应变管线钢不可避免地存在少量工艺缺陷(如焊接缺陷、气泡、夹渣等),当其在外载荷作用下,拉伸应变达到或超过临界值,可能导致管道拉断失效。为了防止拉断失效,拉伸应变需要满足因子化的载荷-阻力设计公式[14]
| $ {\varepsilon _{{\rm{t}}{\kern 1pt} {\rm{f}}}} \le {\phi _{\rm{\varepsilon} {\rm{t}}}}{\varepsilon _{{\rm{t-crit}}}} $ | (25) |
在式(25)中,拉伸应变的阻力因子ϕεt可取0.7,管线钢的拉伸极限应变εt−crit管可由实验确定,且应考虑缺陷、焊缝及热影响区等的影响,当缺乏具体信息时可取0.75%,海底管线的取值为2%[6]。
假设ϕεt取0.7,εt−crit取0.75%,按照式(25)建立的拉伸应变临界值为0.525%。对照图 1可见,此时X52管线钢依然有很大的拉伸空间。考虑到管材缺陷、焊缝及热影响区等的影响,建立管道拉伸应变失效准则为
| $ \varepsilon \le {f_{\rm{s}}}{\phi _{\rm{f}}}[\varepsilon] $ | (26) |
对输油管道,设计系数fs取值为0.72,对输气管道,考虑地区等级:一级地区取0.72,二级地区为0.60,三级地区为0.50,四级地区为0.40;焊缝安全系数ϕf由试验确定,考虑到管材缺陷、焊缝及热影响区等的影响,现场管道无法进行拉伸试验,通常取值为0.6;管道的许用应变[ε]取弹性应变加0.3%的塑性应变,常取0.5%。
需要进行工程临界评价(ECA)和其他附加要求的应变范围为
| $ {f_{\rm{s}}}{\phi _{\rm{f}}}[\varepsilon] \le \varepsilon \le {f_{\rm{s}}}{\phi _{\rm{f}}}{\varepsilon _{\max }} $ | (27) |
当管道局部弯曲时,中性面一侧将发生压缩变形,当管壁最大压应变达到或超过临界应变时,管壁会出现局部屈曲或褶皱。为了防止压缩变形引起的管道失效,文献[11]对压缩应变提出了以下要求
| $ {\varepsilon _{{\rm{cf}}}} \le {\phi _{\rm{\varepsilon} {\rm{c}}}}{\varepsilon _{{\rm{c-crit}}}} $ | (28) |
εc−crit通常由实验确定,且应考虑内压、外压、初始缺陷、残余应力和材料本构关系等因素的影响,缺乏具体信息时按式(29)取值。
| $ {\varepsilon _{{\rm{c- crit}}}} = \left\{ {\begin{array}{*{20}{l}} {0.5\frac{t}{D}- 0.0025 + 3000{{\left[{\frac{{\left( {{p_{\rm{i}}}-{p_{\rm{e}}}} \right)D}}{{2tE}}} \right]}^2}\;\;\;\frac{{\left( {{p_{\rm{i}}} - {p_{\rm{e}}}} \right)D}}{{2t{\sigma _{\rm{s}}}}} < 0.4}\\ {[13pt]0.5\frac{t}{D} -0.0025 + 3000{{\left( {\frac{{0.4{\sigma _{\rm{s}}}}}{E}} \right)}^2}\;\;\;\frac{{\left( {{p_{\rm{i}}} -{p_{\rm{e}}}} \right)D}}{{2t{\sigma _{\rm{s}}}}} \ge 0.4} \end{array}} \right. $ | (29) |
由于管线钢压缩变形多由忽然载荷引起,且呈现局部性,细长管道悬空时的压缩变形还将引起失稳。为安全起见,此处仍沿用式(28)作为压缩变形的失效判据。
3.2.3 椭圆化变形当管道受到外部挤压载荷时,管道横截面可能出现椭圆化变形。管道横截面形状的改变会导致内检测器无法通过,影响管道使用。椭圆化变形率定义为[11]
| $ {\Delta _\rm{\theta} } = 2\left( {{D_{\max }}-{D_{\min }}} \right){\rm{ }}/\left( {{D_{\max }} + {D_{\min }}} \right) $ | (30) |
文献[11]中对管道椭圆化变形的要求为
| $ {\Delta _\rm{\theta} } \le {\Delta _{\rm{\theta} {\rm{ - crit}}}} $ | (31) |
临界椭圆化变形率∆θ−crit通常通过分析或实验确定,或取0.03[5-6]。本文未对椭圆化变形的失效判据进行详尽的分析研究,仍沿用式(31)作为椭圆化变形的失效判据。
4 结论(1) ε≤εP0.2时,Ramberg-Osgood本构方程能够准确地反映X52管线钢的拉伸应力-应变关系,但ε>εP0.2时,Ramberg-Osgood本构模型所得理论本构曲线与实验曲线有较大的误差。
(2) 对Ramberg-Osgood本构模型做出了修正,建立了与实验结果相吻合的全局二段式本构方程;基于mises屈服准则,建立了X52管线钢的本构关系矩阵方程,描述了X52管线钢力学构成的本质特征。
(3) 研究了X52管线钢基于应力的失效判据和基于应变的失效判据,提出了在管道输送工程中应该采用的应力控制失效准则和应变控制失效准则。
符号说明
ε—拉伸应变,无因次;εP0.2—卸载后剩余0.2%的塑性变形所对应的应变,无因次;ε总—总应变,无因次;εe—弹性应变,无因次;εP—塑性应变,无因次;σ—拉应力,MPa;E0—材料初始弹性模量,MPa;K—应变硬化相关系数,MPa;n—应变硬化指数,无因次;σs—材料的屈服极限,MPa;ε0—初始应变,无因次;r—Ramberg-Osgood参数,无因次;σP0.2—卸载后剩余0.2%的塑性变形所对应的应力,MPa;E0.2—应力等于σP0.2时的切线模量,MPa;σP1.0—卸载后剩余1.0%的塑性变形所对应的应力,MPa;n0.2, 1.0—描述σP0.2和σP1.0间曲线段的应变硬化指数,无因次;σe—X52管线钢的比例极限,无因次;σ—应力矩阵,MPa;εP—塑性应变矩阵,无因次;ε—应变矩阵,无因次;Dep—弹塑性矩阵,无因次;D—弹性矩阵,无因次;Dp—塑性矩阵,无因次;εP—等效塑性应变矩阵,无因次;E—弹性模量,MPa;ET—弹塑性模量,MPa;ν—泊松比,无因次;G—剪切弹性模量,MPa;σx,σy,σz—x,y,z向的应力,MPa;τxy,τyz,τzx—xy,yz,zx面上的剪应力,MPa;εx,εy,εz—x,y,z向的应变,无因次;γxy,γyz,γzx—xy,yz,zx面上的剪应变,无因次;σϕ—管道的周向应力,MPa;[σt]—工作温度下管线钢的许用应力,MPa;C—设计系数,无因次;ϕ—焊接接头系数,无因次;pi,po—内压和外压,MPa;Ri,Ro—内径和外径,mm;r′—管道筒体任意一点的半径,mm;τmax最大剪应力,MPa;σr—径向薄膜应力,MPa;σθ—轴向薄膜应力,MPa;σcr—临界应力,MPa;εtf —纵向的因子化拉伸应变,无因次;ϕεt—拉伸应变的阻力因子,无因次;εt−crit —管线钢的拉伸极限应变,无因次;[ε]—许用应变,无因次;ϕf —焊缝系数,无因次;fs—设计系数,无因次;εcf —因子化的纵向或环向压缩应变,无因次;εmax—地面变形中允许的拉应变极限值,取值为2%;ϕεc—压缩应变阻力因子,无因次,可取0.8;εc−crit—管道的纵向或环向压缩极限应变,无因次;t—管道壁厚,mm;D—管道外径,mm;pe—最小外部压力,MPa;∆θ—椭圆化变形率,无因次;Dmax,Dmin—管道的最大和最小外径,mm;∆θ−crit—临界椭圆化变形率,无因次。
| [1] | 贾乃文. 塑性力学[M]. 重庆: 重庆大学出版社, 1992 . |
| [2] |
马廷霞, 吴锦强, 唐愚, 等. 成品油管道的极限悬空长度研究[J].
西南石油大学学报:自然科学版, 2012, 34 (41665) : 173 –173.
Ma Tingxia, Wu Jinqiang, Tang Yu, et al. Maximum suspended length of production pipeline[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2012, 34 (41665) : 173 –173. |
| [3] | 帅健. 管线力学[M]. 北京: 科学出版社, 2010 . |
| [4] | 朱浩川, 姚谏. 不锈钢材料的应力-应变模型[J]. 空间结构, 2011, 17 (1) : 62 –69. |
| [5] | 王孟鸿. 钢结构非线性分析与动力稳定性研究[M]. 北京: 中国建筑工业出版社, 2011 . |
| [6] | 油气及管道建设设计专业标准化委员会. GB50251-2003输气管道工程设计规范[S].北京:中国计划出版社, 2003. |
| [7] | 中国石油天然气集团公司. GB50253-2003输油管道工程设计规范[S].北京:中国计划出版社, 2003. |
| [8] | 王志文, 蔡仁良. 化工容器设计[M]. 北京: 化学工业出版社, 2005 . |
| [9] | Association. CSA Z662-07 oil and gas pipeline systems[S]. Canada:Ontario, 2007. |
| [10] | Det Norske Veritas. DNV-OS-F101 submarine pipeline systems[S]. Norway:Hovik, 2000. |
| [11] | 唐永进. 压力管道应力分析[M]. 北京: 中国石化出版社, 2003 . |
| [12] | 王维, 梁政. 关于悬垂管道计算模型的研究[J]. 天然气工业, 1997, 17 (5) : 63 –66. |
| [13] | 梁政. 石油工程中的若干力学问题[M]. 北京: 石油工业出版社, 1999 . |
| [14] | Liang Chuanpeng. Stress analysis methods for underground pipelines part2-Soil-pipe interaction lines[J]. Pipeline industy, 1978, 5 : 65 –74. |
 2014, Vol. 36
2014, Vol. 36

