水力压裂施工过程中,在裂缝净压力作用下,压裂液向地层滤失,压裂液的滤失对裂缝几何尺寸、支撑剂的分布都有较大的影响,特别是在裂缝性储层中,由于天然裂缝的存在,压裂液的滤失量会更大。
对于裂缝性储层压裂液滤失,国内外做了大量的研究,Penny G等[1]对比了静态和动态条件下压裂液的滤失速度变化,对基岩和裂缝中的滤失控制机理进行了实验评价,指出裂缝对压裂液滤失起控制作用;Barree R D等[2]提出一种随压力变化的压裂液滤失模型,分析对天然裂缝储层进行压裂后,压裂液滤失对裂缝延伸的影响。文献[3]提出了一种考虑多参数的压裂液在双重介质中的滤失模型,考虑了影响滤失量的多种实验参数,压裂液在实际地层中滤失的3个区域,并推导了压裂液在油藏区为双重介质渗流机理控制下滤失速度方程。李勇明等考虑基岩和天然裂缝对压裂液滤失的影响,建立了裂缝性低渗透储层压裂液滤失模型[4-6]。以上对裂缝性储层压裂液滤失模拟研究均对天然裂缝进行了简化处理,未考虑天然裂缝实际分布情况,不能准确描述裂缝性储层压裂液滤失特征。
描述裂缝的参数主要有裂缝的位置、长度、方位、开度、密度等[7-8]。对油气藏内所有的裂缝都进行测量和模拟是不可能的,一般通过测井、录井、地震等方法获得裂缝分布数据,利用概率统计方法得出裂缝几何参数概率分布密度函数,最后运用Monte-Carlo法生成每条裂缝的几何参数:中心点位置、产状、半径和开度[9-11]。
在参考上述方法的基础上,建立储层二维离散裂缝网络模型,借助等效渗透率张量原理将裂缝性介质转化为均质各向异性连续介质,建立了基于渗透率张量的裂缝性储层压裂液滤失数学模型。
1 裂缝性地层压裂液滤失的数学模型 1.1 裂缝性介质整体渗透率等效原理在相同压力梯度和外边界条件下,若同种流体通过相同尺寸的非均质裂缝型介质体和均质各向异性连续介质体的流量相等,则裂缝型介质体可由均质各向异性介质体等效替代,裂缝型介质体的整体渗透率可由均质各向异性介质体的渗透率表示,此即为流量等效原理。对所研究的非均质裂缝型介质区域(图 1a,Γ1,Γ2,Γ3,Γ4-网格边界;n1,n2,n3,n4-网格边界Γ1,Γ2,Γ3,Γ4的单位外法向量)进行网格划分,计算每个网格块的等效渗透率张量,用等效渗透率张量表征的均质各向异性连续介质体代替原裂缝介质体,形成新的等效研究区域(图 1b),即可利用全张量渗透率连续介质渗流理论分析非均质体渗流。
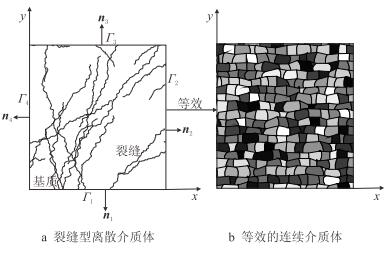 |
| 图1 裂缝性介质等效示意图 Fig. 1 Equivalent schematic diagram of fractured media |
Lee S H等提出对油藏中存在的多级规模的裂缝进行分级处理[12-13],根据裂缝长度lf与离散网格单元尺寸lg的比值,将裂缝划分为三类:短裂缝
基岩和裂缝中的渗流满足达西定律和质量守恒定律
| $ {v_{\rm{m}}} = - \frac{{{K_{\rm{m}}}}}{\mu }\nabla {p_{\rm{m}}} $ | (1) |
| $ {v_{{\rm{f}},i}} = - \frac{{{K_{{\rm{f}},i}}}}{\mu }\nabla {p_{{\rm{f}},i}} $ | (2) |
| $ - \nabla {v_{\rm{m}}} + {q_{{\rm{fm}}}} = 0 $ | (3) |
| $ - \nabla {v_{{\rm{f}},i}} + {q_{{\rm{fm}},i}} = 0 $ | (4) |
式中:
$v_{\rm{m}}$-基岩中的渗流速度,cm/s;
$K_{\rm{m}}$-基岩的渗透率,D;
$\mu$-黏度,mPa.s;
$p_{\rm{m}}$-基岩的孔隙压力,MPa;
$v_{{\rm{f}}, i}$-第i条裂缝的渗流速度,cm/s;
$K_{{\rm{f}}, i}$-第i条裂缝的渗透率,D;
$p_{{\rm{f}}, i}$-第i条裂缝与基岩接触面处的裂缝压力,MPa;
$q_{\rm{fm}}$-基岩和所有裂缝之间的体积流量,cm3/s;
$q_{{\rm{fm}}, i}$-第i条裂缝与周围基岩之间的体积流量,cm3/s。
将运动方程代入连续性方程,得到描述基岩和网格块中第i条裂缝中流体渗流微分方程
| $ \frac{{{K_{\rm{m}}}}}{\mu }\frac{{{\partial ^2}{p_{\rm{m}}}}}{{\partial {x^2}}} + \frac{{{K_{\rm{m}}}}}{\mu }\frac{{{\partial ^2}{p_{\rm{m}}}}}{{\partial {y^2}}} + {q_{{\rm{fm}}}} = 0 $ | (5) |
| $ \frac{{{K_{{\rm{f}},i}}}}{\mu }\frac{{{\partial ^2}{p_{{\rm{f}},i}}}}{{\partial {x^2}}} + \frac{{{K_{{\rm{f}},i}}}}{\mu }\frac{{{\partial ^2}{p_{{\rm{f}},i}}}}{{\partial {y^2}}} + {q_{{\rm{fm}},i}} = 0 $ | (6) |
接触边界条件
| $ {p_{{\rm{f}},i}}{|_\mathit\Omega } = {p_{\rm{m}}}{|_\mathit\Omega } $ | (7) |
| $ ({v_{{\rm{f}},i}}{|_\mathit\Omega }) \cdot \boldsymbol{n} = ({v_{\rm{m}}}{|_\mathit\Omega }) \cdot \boldsymbol{n} $ | (8) |
式中:
$\varOmega$-裂缝与基岩接触面;
$\boldsymbol{n}$-边界的外法向单位向量。
在含有裂缝的正方形基岩网格块中(图 1),网格块的周期边界(纵向Γ1,Γ3;横向Γ2,Γ4条件可表示为[14]
| $ \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {p(x,y = 0) = p(x,y = {l_y}) - {l_y}\frac{{\partial p}}{{\partial y}}}\\ {v(x,y = 0) \cdot {\boldsymbol{n}_{\rm{1}}} = - v(x,y = {l_y}) \cdot {\boldsymbol{n}_{\rm{3}}}} \end{array}}\\ {\begin{array}{*{20}{c}} {p(x = 0,y) = p(x = {l_x},y) - {l_x}\frac{{\partial p}}{{\partial x}}}\\ {v(x = 0,y) \cdot {\boldsymbol{n}_2} = - v(x = {l_x},y) \cdot {\boldsymbol{n}_4}} \end{array}} \end{array}} \right. $ | (9) |
式中:p-压力,MPa;lx,ly-网格x向、y向长度,cm。
通过边界元法对求解区域进行离散,可降低求解的难度,可提高计算精度。因此,可以采用边界元法对上述方程组进行求解。
基岩和裂缝中的渗流方程在本质上来说是Laplace方程
| $ K{\nabla ^2}{p_\varsigma } = 0 $ | (10) |
式中:
K-渗透率,D;
$p_\varsigma ^*$-边界节点处裂缝压力或者基岩压力,MPa。
利用第二格林公式和δ函数的性质,通过极限过程推导出求解区域边界上各点的边界积分方程,其一般的形式为
| $ {c^i}{p_\varsigma }^i + \int\limits_\varsigma {v_\varsigma ^*{p_\varsigma }{\rm{d}}\mathit\Gamma } = \int\limits_\varsigma {{v_\varsigma }p_\varsigma ^*{\rm{d}}\mathit\Gamma } $ | (11) |
其中
| $ {c^i} = \frac{{{\alpha _i}}}{{2{\rm{\pi }}}} $ | (12) |
| $ p_\varsigma ^{\rm{*}} = \frac{1}{{2{\rm{\pi }}K}}\ln \frac{{\sqrt K }}{r} $ | (13) |
| $ v_\varsigma ^{\rm{*}} = K\frac{{\partial p_\varsigma ^{\rm{*}}}}{{\partial {n_i}}} $ | (14) |
| $ r = \sqrt {{{\left( {x - {x_{\rm{i}}}} \right)}^2} + {{\left( {y - {y_{\rm{i}}}} \right)}^2}} $ | (15) |
式中:
c-系数,无因次;
$p_\varsigma ^*$-渗流方程的Laplace基本解,MPa;
${v_\varsigma }$-边界节点处的外法向裂缝渗流速度或基岩渗流速度,cm/s;
$v_\varsigma ^*$-Laplace方程的基本解的外法向导数与渗透率的乘积,cm/s;
$\varGamma $-网格块外边界或基岩与裂缝的交界面。
为了计算方便,采用常单元对求解区域进行剖分,将边界Γ分为N个小单元,以各小单元的中点为节点。对边界积分方程进行分段积分,可得
| $ {c^i}{p^i} + \sum\limits_{j = 1}^N {\int\limits_{{\mathit\Gamma _{\rm{j}}}} {{v^*}p{\rm{d}}\mathit\Gamma } } = \sum\limits_{j = 1}^N {\int\limits_{{\mathit\Gamma _{\rm{j}}}} {{p^*}v{\rm{d}}\mathit\Gamma } } $ | (16) |
根据常单元的特性,以每一个单元上的节点值代替单元上的值,即在每一个单元上pj和vj是常数,则有
| $ {c^i}{p^i} + \sum\limits_{j = 1}^N {\left( {\int\limits_{{\mathit\Gamma _{\rm{j}}}} {{v^*}{\rm{d}}\mathit\Gamma } } \right)} {p_j} = \sum\limits_{j = 1}^N {\left( {\int\limits_{{\mathit\Gamma _{\rm{j}}}} {{p^*}{\rm{d}}\mathit\Gamma } } \right){v_j}} $ | (17) |
p*和v*是基本解及其法向导数,它们在每一个单元上的积分是已知的。式(17)可化为
| $ \begin{array}{*{20}{c}} {\sum\limits_{j = 1}^N {{H_{i,j}}{p_j}} = \sum\limits_{j = 1}^N {{G_{i,j}}{v_j}} } \end{array} $ | (18) |
式中
全部节点离散后得到方程组可表示为
| $ \boldsymbol{Hp} = \boldsymbol{Gv} $ | (19) |
式中:
| $ \mathit{\pmb{H}}=\left[\begin{matrix} {{H}_{11}} & {{H}_{12}} & \cdots & {{H}_{1N}} \\ {{H}_{21}} & {{H}_{22}} & \cdots & {{H}_{2N}} \\ \cdots & \cdots & \cdots & \cdots \\ {{H}_{N1}} & {{H}_{N2}} & \cdots & {{H}_{NN}} \\ \end{matrix} \right]; $ |
| $ \boldsymbol{G}=\left[\begin{matrix} {{H}_{11}} & {{H}_{12}} & \cdots & {{H}_{1N}} \\ {{H}_{21}} & {{H}_{22}} & \cdots & {{H}_{2N}} \\ \cdots & \cdots & \cdots & \cdots \\ {{H}_{N1}} & {{H}_{N2}} & \cdots & {{H}_{NN}} \\ \end{matrix} \right]; $ |
| $ \boldsymbol{p}={{\left[\begin{matrix} {{p}_{1}} & {{p}_{2}} & \cdots & {{p}_{N}} \\ \end{matrix} \right]}^{\text{T}}}={{\left[\begin{matrix} {{v}_{1}} & {{v}_{2}} & \cdots & {{v}_{N}} \\ \end{matrix} \right]}^{\text{T}}}。 $ |
求解全部节点离散后得到方程组,通过等效渗透率张量原理计算,得到裂缝型介质的等效渗透率张量。
1.3 压裂液在地层中渗流模型利用前面计算的渗透率全张量表征储层的渗透性,假设压裂液微可压缩,渗流符合达西定律,并忽略重力影响,二维单相渗流的广义达西公式和连续性方程为
| $ v=-\frac{K}{{{\mu }_{\text{e}}}}\cdot \nabla p $ | (20) |
| $ n-\nabla (\rho v)=\frac{\partial (\rho \phi )}{\partial t} $ | (21) |
式中:
v-渗流速度,cm/s;
$\rho$-密度,g/cm3;
$\phi$-孔隙度,%;
t-时间,s。
渗流速度的分量形式
| $ n-\frac{1}{B}\left( \frac{\partial {{v}_{x}}}{\partial x}+\frac{\partial {{v}_{y}}}{\partial x} \right)={{C}_{\text{l}}}\frac{\partial p}{\partial t} $ | (22) |
式中:
$v_x$,$v_y$-x向,y向渗流速度,cm/s;
${\mu _{\rm{e}}}$-压裂液的有效黏度,mPa.s;
B-压裂液体积系数,无因次;
$C_{\rm{l}}$-压裂液的综合压缩系数,MPa-1。
封闭外边界条件
| $ \left\{ {\begin{array}{*{20}{l}} {{{\left. {\frac{{\partial p}}{{\partial y}}} \right|}_{y = {W_y}}} = 0}\\ {{{\left. {\frac{{\partial p}}{{\partial x}}} \right|}_{x = {W_x}}} = 0}\\ {{{\left. {\frac{{\partial p}}{{\partial x}}} \right|}_{x = 0}} = 0}\\ {{{\left. {\frac{{\partial p}}{{\partial y}}} \right|}_{({L_{\rm{f}}} < x{W_x},y = 0)}} = 0} \end{array}} \right. $ | (23) |
式中:
$W_x$、$W_y$-研究区域x方向、y方向的长度,m;
$L_{\rm{f}}$-裂缝长度,m。
内边界条件和初始条件分别为
| $ {\left. p \right|_{(x{L_{\rm{f}}},y = 0)}} = {p_{\rm{f}}} $ | (24) |
| $ {\left. p \right|_{t = 0}} = {p_{\rm{i}}} $ | (25) |
式中:
$p_{\rm{f}}$-人工裂缝压力,MPa;
$p_{\rm{i}}$-初始压力,MPa。
2 实例分析在200 m×200 m的区域内,生成符合如下分布规律的离散裂缝网络:裂缝位置均匀分布;裂缝倾角符合正态分布,均值为60°,标准差20°;裂缝长度符合正态分布,均值为1.5 m,标准差为0.4 m;裂缝开度符合正态分布,均值为90 µm,标准差20 µm。结合储层基本参数(表 1),进行模拟计算。
| 表1 储层基本参数 Table 1 Basic data of reservoir |
根据上述数据生成储层离散裂缝网络模型,并划分网格计算每个网格的等效渗透率分布,如图 2所示,其中用红线所圈部分为人工裂缝与天然裂缝的相交位置。将网格的裂缝分布情况与等效后的渗透率张量进行对比,可知基岩渗透率、裂缝密度、裂缝开度和裂缝方位等参数对裂缝性介质的渗透率张量都有影响,长裂缝对相应网格的等效渗透率张量起主要控制作用,短裂缝对等效渗透率张量的影响相对较小,不含裂缝网格块的等效渗透率张量就是基岩的渗透率。
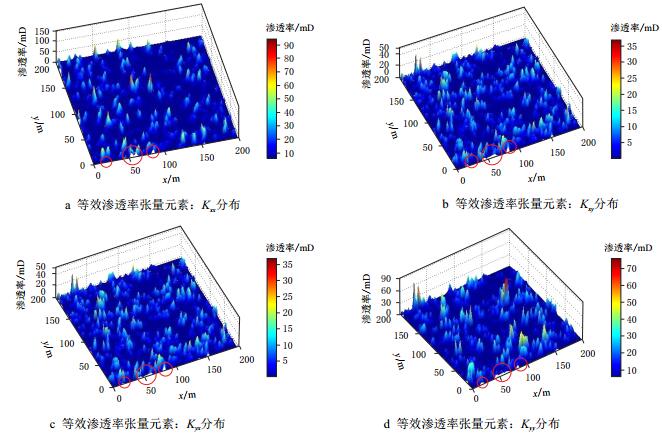 |
| 图2 裂缝性储层等效渗透率分布图 Fig. 2 Equivalent permeability tensor distribution of fractured reservoir |
在计算渗透率张量的基础上,模拟了压裂施工10 min和60 min时,水力裂缝一侧压力分布,如图 3所示。从图 3中可以看出由于天然裂缝分布的非均匀性,造成压力传播的不均匀。
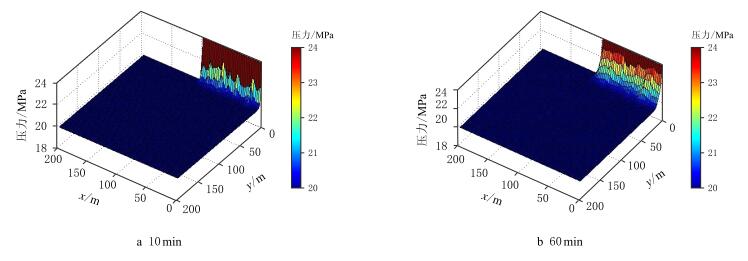 |
| 图3 不同时刻压力分布 Fig. 3 Pressure distribution at different times |
图 4为压裂施工10 min、60 min时水力裂缝一侧压裂液滤失速度分布,由于水力裂缝一侧天然裂缝分布的不均匀性以及与水力裂缝的位置关系不同,使沿裂缝长度方向压裂液的滤失速度变化较大,
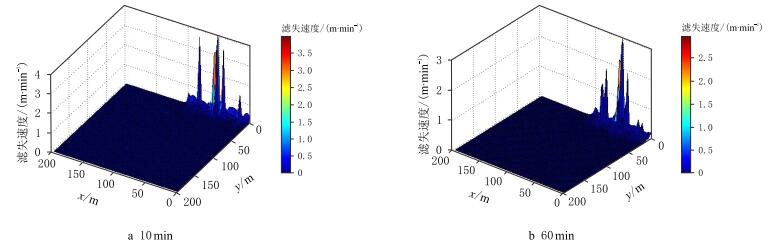 |
| 图4 不同时刻压裂液滤失速度分布 Fig. 4 Fracturing fluid leakoff velocity distribution at different times |
尤其当某处天然裂缝与水力裂缝连通时,该处的压裂液滤失速度明显增大%(图 2中标注了天然裂缝与水力裂缝相交的位置),对比发现这几处的压裂液滤失速度是其他位置的3~4倍。进而研究了这几处在不同时间的滤矢量与总滤失量之间的关系,发现这几处的滤失量占总滤失量的45%以上,如图 5所示。所以在对裂缝性储层进行压裂施工时,要对压裂液的性能进行调整,以适应裂缝性储层的要求。
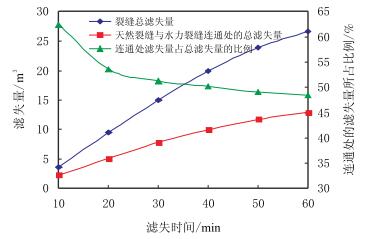 |
| 图5 水力裂缝总滤失量随时间的变化 Fig. 5 Total filtration distribution of hydraulic fracture |
随着裂缝净压力的增加,裂缝不同位置处的滤失速度均有所增加,但是不同位置处滤失速度增加的程度不同(图 6)。天然裂缝与人工裂缝连通处的滤失速度的增加幅度远大于其他各处,这是由于:(1)裂缝净压力的增加,使滤失压差增加,滤失量增加;(2)裂缝净压力的增加,使天然裂缝开度增加,从而增加了天然裂缝的渗流能力,使滤失速度增加。
 |
| 图6 水力裂缝延伸方向滤失速度随裂缝净压力的变化 Fig. 6 Filtration rate of different fracture net pressure at hydraulic fracture propagation direction |
(1)提出了基于离散裂缝网络的裂缝性储层压裂液滤失模型,综合考虑了油藏边界、压裂液的非牛顿特性以及储层的天然裂缝分布,计算结果更符合实际。
(2)天然裂缝分布及其与水力裂缝的位置关系的不同,使得沿裂缝长度方向,滤失速度变化较大,若天然裂缝与水力裂缝连通,则压裂液滤失主要发生在连通处,当天然裂缝和人工裂缝存在三处连通时,这三处的滤失量占裂缝总滤失量的45%以上。所以,在裂缝性储层压裂施工中,需考虑压裂液的降滤性以及对天然裂缝的封堵性能。
(3)由于该模型在很大程度上依赖于储层复杂的天然裂缝分布,所以在如何获取更为准确的天然裂缝分布参数方面,有待进一步研究。
| [1] | Penny G, Conway M, Lee W. Control and modeling of fluid leakoff during hydraulic fracturing[C]. SPE 12486, 1985. https://www.onepetro.org/journal-paper/SPE-12486-PA |
| [2] | Barree R D, Mukherjee H. Determination of pressure dependent leakoff and its effect on fracture geometry[C]. SPE 36424, 1996. https://www.onepetro.org/conference-paper/SPE-36424-MS |
| [3] |
付永强, 郭建春, 赵金洲, 等. 一种多参数的压裂液在双重介质中滤失模型的推导与计算[J].
天然气工业, 2003, 23 (3) : 88 –91.
Fu Yongqiang, Guo Jianchun, Zhao Jinzhou, et al. A multi-parameter fracturing fluid filtration model in a dual media[J]. Natural Gas Industry, 2003, 23 (3) : 88 –91. |
| [4] |
李勇明, 郭建春, 赵金洲, 等. 裂缝性气藏压裂液滤失模型的研究及应用[J].
石油勘探与开发, 2004, 31 (5) : 120 –122.
Li Yongming, Guo Jianchun, Zhao Jinzhou, et al. Research and application of fracturing fluid filtration model in fractured gas reservoir[J]. Petroleum Exploration and Development, 2004, 31 (5) : 120 –122. |
| [5] |
李勇明, 赵金洲, 郭建春, 等. 裂缝性低渗透储层压裂液滤失计算新模型[J].
石油钻采工艺, 2004, 26 (5) : 44 –46.
Li Yongming, Zhao Jinzhou, Guo Jianchun, et al. The new model of fracturing fluid loss in fractured low permeability reservoir[J]. Oil Drilling & Production Technology, 2004, 26 (5) : 44 –46. |
| [6] |
李勇明, 郭建春, 赵金洲, 等. 裂缝性储层压裂液滤失计算模型研究[J].
天然气工业, 2005, 25 (3) : 99 –101.
Li Yongming, Guo Jianchun, Zhao Jinzhou, et al. The research on the calculation model of fracturing fluid loss in fractured reservoir[J]. Natural Gas Industry, 2005, 25 (3) : 99 –101. |
| [7] | Tamagawa T, Matsuura T, Anraku T, et al. Construction of fracture network model using static and dynamic data[C]. SPE 77741, 2002. https://www.researchgate.net/publication/254513311_Construction_of_Fracture_Network_Model_Using_Static_and_Dynamic_Data |
| [8] |
蒲静, 秦启荣. 油气储层裂缝预测方法综述[J].
特种油气藏, 2008, 15 (3) : 9 –13.
Pu Jing, Qin Qirong. Summary of forecasting methods of reservoir fracture oil and gas[J]. Special Oil & Gas Reservoirs, 2008, 15 (3) : 9 –13. |
| [9] | 陈剑平, 肖树芳, 王清. 随机不连续面三维网络计算机模拟原理[M]. 长春: 东北师范大学出版社, 1995 . |
| [10] |
宋晓晨, 徐卫亚. 裂隙岩体渗流模拟的三维离散裂隙网络数值模型(I):裂隙网络的随机生成[J].
岩石力学与工程学报, 2004, 23 (12) : 2015 –2020.
Song Xiaochen, Xu Weiya. Numerical model of threedimensional discrete fracture network seepage in fractured rocks (I):Random fracture network[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23 (12) : 2015 –2020. |
| [11] |
冯学敏, 陈胜宏. 含复杂裂隙网络岩体渗流特性研究的复合单元法[J].
岩石力学与工程学报, 2006, 25 (5) : 918 –924.
Feng Xuemin, Chen Shenghong. The study of complex fracture network seepage characteristic of rock by Composite element method[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25 (5) : 918 –924. |
| [12] | Lee S H, CL Jensen L, Lough M. An efficient finite difference model for flow in a reservoir with multiple lengthscale fractures[C]. SPE 56752, 2004. https://www.onepetro.org/conference-paper/SPE-56752-MS |
| [13] | He N, Lee S H, Jensen C L. Combination of analytical, numerical and geostatistical methods to model naturally fractured reservoirs[C]. SPE 68832, 2001. https://www.onepetro.org/conference-paper/SPE-68832-MS |
| [14] | Durlofsky L J. Numerical calculation of equivalent grid block permeability tensors for heterogeneous porous media[J]. Water Resources Research, 1991, 27 (5) : 699 –708. DOI:10.1029/91WR00107 |
 2014, Vol. 36
2014, Vol. 36

