2. 中国石化新星石油有限责任公司, 北京 海淀 100083;
3. 中国石化西南油气分公司勘探开发研究院, 四川 成都 610081;
4. 北京邮电大学计算机学院, 北京 海淀 100876
2. Star Petroleum Co. Ltd., SINOPEC, Haidian, Beijing 100083, China;
3. Exploration & Production Institute of Southwest Petroleum Branch Company, SINOPEC, Chengdu, Sichuan 610081, China;
4. School of Computer Science, Beijing University of Posts and Telecommunications, Haidian, Beijing 100876, China
中国低渗气藏分布广泛,初步统计,在大中型气田中,低渗气藏储量约占所有气藏储量的59.8%。同时,随着勘探开发技术水平的不断提高,发现低渗气藏的比例将会逐年增加。因此,如何开发这类气藏将对中国天然气工业的持续稳定发展产生深远的影响。水平井因其具有生产压差小、泄流面积大等特点被广泛地应用于低渗气藏的开发,近年来在川西、大牛地、苏里格、塔里木等发展相当迅猛[1-8]。孙来喜、杨滨、胥洪俊、郑丽坤,蒋艳芳等,分析了应力敏感对气藏产能的影响,认为考虑应力敏感时计算的气井无阻流量与不考虑应力敏感的计算值相差较大,且随应力敏感性的增强而变大,不能忽视气井的应力敏感性[9-13];孟令强、李乐忠、郭晶晶等,研究启动压力梯度对低渗气藏气井产能的影响,同样认为对低渗气藏而言,启动压力梯度是一个重要的影响因素,应充分考虑其对气井产能的影响[14-16]。如果不完全考虑启动压力梯度、应力敏感的影响,这必然会造成计算出来的无阻流量偏高,不利于指导气藏的合理开发。本文在Forchheimer渗流方程的基础上引入启动压力梯度和应力敏感系数,建立低渗气藏拟稳定渗流水平井二项式产能修正方程,以川西地区某气藏实例论证了二项式产能修正方程的可靠性,并对启动压力梯度和应力敏感对低渗气藏水平井产能的影响进行了分析,最后以该气藏的某典型水平井验证了修正二项式产能方程的适用性。
1 低渗气藏气井产能方程由于应力敏感效应和启动压力梯度在低渗气藏开发过程中的重要影响,因此,有必要引入应力敏感系数和启动压力梯度以修正低渗气藏气井产能方程[17-19]。根据Forcheimer方程
| $ \frac{{{\rm{d}}p}}{{{\rm{d}}r}} = \frac{{{\mu _{\rm{g}}}}}{K} \cdot v + \beta \rho {v^2} $ | (1) |
式中:p-某时刻地层压力,MPa;
r-径向流动半径,m;
$\mu_{\rm{g}}$-气体黏度,Pa·s;
K-有效渗透率,mD;
v-气体速度,m/s;
$\beta$-描述孔隙介质紊流影响的系数,m-1;
$\rho$-气体密度,kg/m3。
引入启动压力梯度λ
| $ \frac{{{\rm{d}}p}}{{{\rm{d}}r}} - \lambda = \frac{{{\mu _{\rm{g}}}}}{K} \cdot v + \beta \rho {v^2} $ | (2) |
式中:λ-启动压力梯度,MPa/m。
考虑应力敏感效应
| $ K = {K_{\rm{i}}}{{\rm{e}}^{ - {a_{\rm{k}}}({p_{\rm{i}}} - p)}} $ | (3) |
式中:$K_{\rm{i}}$-气藏原始渗透率,mD;
$a_{\rm{k}}$-应力敏感指数,MPa-1;
$p_{\rm{i}}$-原始地层压力,MPa。
式(1)中右端第二项代表非达西流动部分压降,它主要发生在井壁附近,可视为与流量相关的表皮。根据李士伦[20]这部分压降(ΔpnD)可定量表示为
| $ {\rm{d}}{p_{n{\rm{D}}}} = \beta \rho {v^2}{\rm{d}}r $ | (4) |
| $ \beta ={7.644\times {{10}^{10}}}/{{{K}^{1.5}}}\; $ | (5) |
| $ \rho = \frac{{28.97{\gamma _{\rm{g}}}p}}{{Z{\rm{R}}T}} $ | (6) |
式中:ΔpnD-非达西流动压降,无因次;
${\mathit\gamma _{\rm{g}}}$-天然气相对密度,无因次;
Z-气体偏差系数,无因次;
R-常数,R=8.314 J/(mol·K);
T-气藏温度,K。
因此,在建立低渗气藏气井产能方程的时,可先忽略这部分非达西流动(附加压降)的影响,待建立产能方程后,再将非达西流动能耗叠加到产能方程中。
平面径向稳定渗流的产量
| $ q = 2{\rm{\pi }}rhv $ | (7) |
将产量换算至地面
| $ q = {B_{\rm{g}}}{q_{{\rm{sc}}}} = \frac{{ZT{p_{{\rm{sc}}}}}}{{{Z_{{\rm{sc}}}}{T_{{\rm{sc}}}}p}}{q_{{\rm{sc}}}} $ | (8) |
联立式(2)、式(3)、式(7)、式(8)求解可得
| $ {{\rm{e}}^{{a_{\rm{k}}}p}}\frac{{2p}}{{{\mu _{\rm{g}}}Z}}{\rm{d}}p - \lambda {{\rm{e}}^{{a_{\rm{k}}}p}}\frac{{2p}}{{{\mu _{\rm{g}}}Z}}{\rm{d}}r = \frac{{{q_{{\rm{sc}}}}{{\rm{e}}^{{a_{\rm{k}}}{p_{\rm{i}}}}}}}{{{\rm{\pi }}{K_{\rm{i}}}\alpha h}}\frac{1}{r}{\rm{d}}r $ | (9) |
其中
| $ \alpha = \frac{{{Z_{{\rm{sc}}}}{T_{{\rm{sc}}}}}}{{{p_{{\rm{sc}}}}T}} $ | (10) |
定义拟压力
| $ \psi (p) = \int {{{\rm{e}}^{{a_{\rm{k}}}p}}\frac{{2p}}{{{\mu _{\rm{g}}}Z}}} {\rm{d}}p $ | (11) |
式中:q-水平气井产能,×104 m3/d;
h-气层厚度,m;
${B_{\rm{g}}}$-天然气体积系数,无因次;
${q_{{\rm{sc}}}}$-水平气井产能(地面),×104 m3/d;
${p_{{\rm{sc}}}}$-标况下的压力,MPa;
${Z_{{\rm{sc}}}}$-标况下的偏差系数,无因次;
${T_{{\rm{sc}}}}$-标况下的温度,K。
将式(8)两边分别从(rw, pwf)到(re, pe)积分,并根据平均压力法,取平均压力
| $ {q_{{\rm{sc}}}} = \frac{{{\rm{\pi }}{Z_{{\rm{sc}}}}{T_{{\rm{sc}}}}{K_{\rm{i}}}h[\psi ({p_{\rm{e}}}) - \psi ({p_{{\rm{wf}}}}) - \lambda \frac{{2\bar p}}{{\overline {{\mu _{\rm{g}}}} \bar Z}}{{\rm{e}}^{{a_{\rm{k}}}\bar p}}({r_{\rm{e}}} - {r_{\rm{w}}})]}}{{{{\rm{e}}^{{a_{\rm{k}}}{p_{\rm{i}}}}}{p_{{\rm{sc}}}}T\ln \frac{{{r_{\rm{e}}}}}{{{r_{\rm{w}}}}}}} $ | (12) |
将式(6)、式(7)、式(8)代入式(4)可得
| $ {\rm{d}}{p_{n{\rm{D}}}} = \frac{{28.97\beta {\gamma _{\rm{g}}}ZTp_{{\rm{sc}}}^2q_{{\rm{sc}}}^2}}{{4{{\rm{\pi }}^2}{h^2}T_{{\rm{sc}}}^2Rp{r^2}}}{\rm{d}}r $ | (13) |
式中:${p_{\rm{e}}}$-供给边界压力,MPa;
$p_{{\rm{wf}}}$-井底流压,MPa;
$\overline p$-平均地层压力,MPa;
$\overline {{\mu _{\rm{g}}}} $-平均压力和温度下的平均气体黏度,mPa·s;
$\overline Z$-平均压力和温度下的气体偏差因子,无因次;
${r_{\rm{e}}}$-供给半径,m;
${r_{\rm{w}}}$-井径,m。
将式(12)整理,得
| $ 2p \cdot {\rm{d}}{p_{n{\rm{D}}}} = \frac{{28.97\beta {\gamma _{\rm{g}}}ZTp_{{\rm{sc}}}^2q_{{\rm{sc}}}^2}}{{2{{\rm{\pi }}^2}{h^2}T_{{\rm{sc}}}^2R}}\frac{1}{{{r^2}}}{\rm{d}}r\% $ | (14) |
同样将式(13)两边从(rw, pwf)到(re, pe)积分,根据平均压力法,求气体的平均黏度和平均偏差因子,并认为它们在积分范围内为常数,可得到气井非达西流动产生的能耗ΔpnD2
| $ \Delta p_{n{\rm{D}}}^2 = \frac{{28.97\beta {\gamma _{\rm{g}}}\bar ZTp_{{\rm{sc}}}^{\rm{2}}q_{{\rm{sc}}}^2}}{{2{{\rm{\pi }}^2}{h^2}T_{{\rm{sc}}}^{\rm{2}}{\rm{R}}}}\left( {\frac{1}{{{r_{\rm{w}}}}} - \frac{1}{{{r_{\rm{e}}}}}} \right) $ | (15) |
假设一口长度为L的水平井钻入气层中央,气层厚度为h,气层为圆形、水平、顶、底边界不渗透,且气体渗流满足:气体为单相渗流,且渗流过程组分不发生变化;渗流过程符合高速非达西渗流定律,并忽略重力影响;渗流过程忽略温度变化。
根据陈元千的研究[21],将水平井的渗流场分为平面和垂面两个连续渗流场(图 1,图 2)。平面渗流场的长、短半轴长分别为a、b。
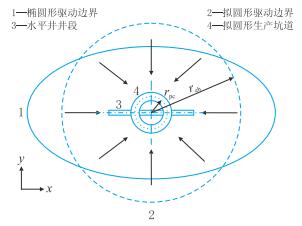 |
| 图1 水平井平面椭圆渗流场转换 Fig. 1 The transformation of horizontal well flat ellipse seepage field |
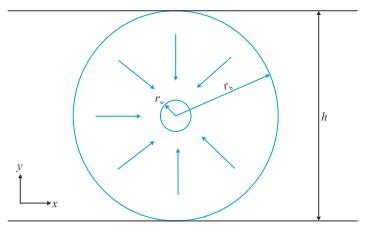 |
| 图2 水平井垂面平面径向流 Fig. 2 The vertical plane radial flow of horizontal well |
对于平面渗流场,这时内、外边界和平面渗流阻力分别为
| $ \left\{ {\begin{array}{*{20}{l}} {{r_{\rm{e}}} = {r_{{\rm{eh}}}} = \sqrt {{{(a - L/4)}^2} - {{(L/4)}^2}} }\\ {{r_{\rm{w}}} = {r_{{\rm{pc}}}} = L/4 + h/2} \end{array}} \right. $ | (16) |
| $ {R_{\rm{h}}} = \frac{{{{\rm{e}}^{{a_{\rm{k}}}{p_{\rm{i}}}}}{p_{{\rm{sc}}}}T}}{{{\rm{\pi }}{K_{\rm{i}}}h{Z_{{\rm{sc}}}}{T_{{\rm{sc}}}}}}\ln \sqrt {{{\left( {4a/L - 1} \right)}^2} - 1} $ | (17) |
式中:$r_{{\rm{eh}}}$-拟圆形驱动半径,m;
a-椭圆长半轴,m;
L-水平井长度,m;
$r_{{\rm{pc}}}$-拟生产坑道半径,m;
${R_{\rm{h}}}$-水平面的渗流阻力,无因次。
垂面渗流场,这时内、外边界和平面渗流阻力分别为
| $ \left\{ {\begin{array}{*{20}{l}} {{r_{\rm{e}}} = {r_{\rm{b}}} = h/2}\\ {{r_{\rm{w}}} = {r_{\rm{w}}}} \end{array}} \right. $ | (18) |
| $ {R_{\rm{v}}} = \frac{{{{\rm{e}}^{{a_{\rm{k}}}{p_{\rm{i}}}}}{p_{{\rm{sc}}}}T}}{{{\rm{\pi }}{K_{\rm{i}}}L{Z_{{\rm{sc}}}}{T_{{\rm{sc}}}}}}\ln \frac{h}{{2{r_{\rm{w}}}}} $ | (19) |
式中:${r_{\rm{b}}}$-垂直面的供给半径,m;
${R_{\rm{v}}}$-垂直面的渗流阻力,无因次。
根据等值渗流阻力法
| $ {q_{{\rm{sc}}}} = \frac{{{\rm{\pi }}{Z_{{\rm{sc}}}}{T_{{\rm{sc}}}}{K_{\rm{i}}}h[\psi ({p_{\rm{e}}}) - \psi ({p_{{\rm{wf}}}}) - \lambda \frac{{2\bar p}}{{\overline {{\mu _{\rm{g}}}} \bar Z}}{{\rm{e}}^{{a_{\rm{k}}}\bar p}}({r_{\rm{e}}} - {r_{\rm{w}}})]}}{{{{\rm{e}}^{{a_{\rm{k}}}{p_{\rm{i}}}}}{p_{{\rm{sc}}}}T\left[{\ln \sqrt {{{(4a/L - 1)}^2} - 1} + \frac{h}{L}\ln \frac{h}{{2{r_{\rm{w}}}}}} \right]}} $ | (20) |
再将转换后的水平井平面渗流场和垂面渗流场的供给半径re和井径rw,代入式(19),可得考虑应力敏感和启动压力梯度水平井产能方程:(拟压力形式)
| $ q = \frac{{{\rm{\pi }}{Z_{{\rm{sc}}}}{T_{{\rm{sc}}}}{K_{\rm{i}}}h\left[{\psi ({p_{\rm{e}}}) - \psi ({p_{{\rm{wf}}}}) - \lambda {{\rm{e}}^{{a_{\rm{k}}}\bar p}}\frac{{2\bar p}}{{\overline {{\mu _{\rm{g}}}} \bar Z}}\left( {\sqrt {{a^2} - \frac{{aL}}{2}} - \frac{L}{4} - {r_{\rm{w}}}} \right)} \right]}}{{{{\rm{e}}^{{a_{\rm{k}}}{p_{\rm{i}}}}}{p_{{\rm{sc}}}}T\left[{\ln \sqrt {{{(4a/L - 1)}^2} - 1} + \frac{h}{L}\ln \frac{h}{{2{r_{\rm{w}}}}}} \right]}} $ | (21) |
引入非达西项压降
| $ \Delta p_{n{\rm{D}}}^2 = \frac{{28.97\beta {\gamma _{\rm{g}}}\bar ZTp_{{\rm{sc}}}^2q_{{\rm{sc}}}^{\rm{2}}}}{{2{{\rm{\pi }}^2}{h^2}T_{{\rm{sc}}}^2{\rm{R}}}}\left( {\frac{1}{{{r_{\rm{w}}}}} + \frac{4}{{L + 2h}} - \frac{2}{h} - \frac{4}{{\sqrt {2{a^2} + aL} }}} \right) $ | (22) |
根据式(20)、式(21)可得到考虑应力敏感、启动压力梯度的低渗气藏水平井产能方程(拟压力形式)
| $ \left\{ {\begin{array}{*{20}{l}} {\psi ({p_{\rm{e}}}) - \psi ({p_{{\rm{wf}}}}) - \lambda {{\rm{e}}^{({a_{\rm{k}}}\bar p)}}.\frac{{2\bar p}}{{\overline {{\mu _{\rm{g}}}} \bar Z}}\left( {\sqrt {{a^2} - \frac{{aL}}{2}} - \frac{L}{4} - {r_{\rm{w}}}} \right) = Aq + B{q^2}}\\ {A = \frac{{{{\rm{e}}^{({a_{\rm{k}}}{p_{\rm{i}}})}}{p_{{\rm{sc}}}}T\left[{\ln \sqrt {{{\left( {\frac{{4a}}{L} - 1} \right)}^2} - 1} + \frac{h}{L}\ln \frac{h}{{2{r_{\rm{w}}}}}} \right]}}{{{\rm{\pi }}{Z_{{\rm{sc}}}}{T_{{\rm{sc}}}}{K_{\rm{i}}}h}}}\\ {B = \frac{{28.97\beta {\gamma _{\rm{g}}}\bar ZTp_{{\rm{sc}}}^2}}{{2{{\rm{\pi }}^2}{h^2}T_{{\rm{sc}}}^2R}}\left( {\frac{1}{{{r_{\rm{w}}}}} + \frac{4}{{L + 2h}} - \frac{2}{h} - \frac{4}{{\sqrt {2{a^2} + aL} }}} \right)} \end{array}} \right. $ | (23) |
根据川西新场气田岩芯实验和马飞[22]等研究,川西某气藏的应力敏感系数为0.041 MPa-1,启动压力梯度为0.002 5 MPa/m,根据该气藏某气井的系统试井数据(表 1),分别论证应力敏感和启动压力梯度对无阻流量的影响。
| 表1 川西某水平井系统试井数据表 Table 1 System well testing data of a horizontal well in western Sichuan |
经过拟合,得到常规二项式产能方程:
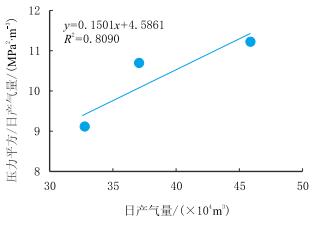 |
| 图3 常规二项式产能方程 Fig. 3 Conventional binomial productivity equation |
当只考虑启动压力梯度时(即ak=0),求解式(22)可得只考虑启动压力梯度的低渗气藏二项式产能方程(压力平方形式)
| $ \left\{ {\begin{array}{*{20}{l}} {p_{\rm{e}}^{\rm{2}} - p_{{\rm{wf}}}^2 - C = A \cdot (\overline {{\mu _{\rm{g}}}} \bar Z)q + B \cdot (\overline {{\mu _{\rm{g}}}} \bar Z){q^2}}\\ {C = \lambda \cdot 2\bar p(\sqrt {{a^2} - \frac{{a \cdot L}}{2}} - \frac{L}{4} - {r_{\rm{w}}})} \end{array}} \right. $ | (24) |
当取启动压力梯度为0.002 5 MPa/m,将测试数据用于考虑启动压力梯度的产能方程进行拟合,得到的产能曲线如图 4所示。
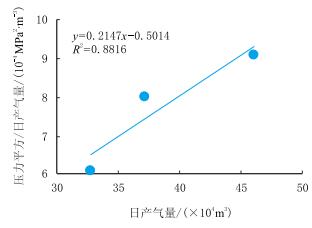 |
| 图4 考虑启动压力梯度的二项式产能方程 Fig. 4 The binomial productivity equation considering start-up pressure gradient |
经过拟合,得到考虑启动压力梯度的二项式产能方程:
当只考虑应力敏感时(即λ=0),求解式(22)可得只考虑应力敏感的低渗气藏二项式产能方程(压力形式)
| $ \begin{array}{l} \frac{1}{{{a_{\rm{k}}}}}[{p_{\rm{e}}} \cdot {{\rm{e}}^{{a_{\rm{k}}} \cdot {p_{\rm{e}}}}} - {p_{{\rm{wf}}}} \cdot {{\rm{e}}^{{a_{\rm{k}}} \cdot {p_{{\rm{wf}}}}}}] - \frac{1}{{{a_{\rm{k}}}^2}}[{{\rm{e}}^{{a_{\rm{k}}} \cdot {p_{\rm{e}}}}} - {{\rm{e}}^{{a_{\rm{k}}} \cdot {p_{{\rm{wf}}}}}}] = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;A \cdot (\overline {{\mu _{\rm{g}}}} \bar Z)q + B \cdot (\overline {{\mu _{\rm{g}}}} \bar Z){q^2} \end{array} $ | (25) |
当取应力敏感系数为0.041 MPa-1,将测试数据用于考虑应力敏感的产能方程进行拟合,得到的产能曲线如图 5所示。
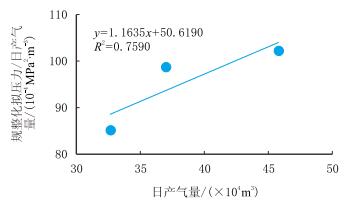 |
| 图5 考虑应力敏感的二项式产能方程 Fig. 5 The binomial productivity equation considering stress sensitive |
经过拟合,得到考虑应力敏感的二项式产能方程
| $ \begin{array}{l} \frac{1}{{{a_{\rm{k}}}}}[{p_{\rm{e}}} \cdot {{\rm{e}}^{{a_{\rm{k}}} \cdot {p_{\rm{e}}}}} - {p_{{\rm{wf}}}} \cdot {{\rm{e}}^{{a_{\rm{k}}} \cdot {p_{{\rm{wf}}}}}}] - \frac{1}{{{a_{\rm{k}}}^2}}[{{\rm{e}}^{{a_{\rm{k}}} \cdot {p_{\rm{e}}}}} - {{\rm{e}}^{{a_{\rm{k}}} \cdot {p_{{\rm{wf}}}}}}] = \\ \;\;\;\;\;\;\;\;\;\;\;50.619q + 1.1635{q^2} \end{array} $ | (26) |
相关系数R2=0.7590,进而可由式(26)求得考虑应力敏感系数为0.04 1 MPa-1时的无阻流量为111.76×104 m3/d。
| $ {q_{{\rm{AOF}}}} = \frac{{\sqrt {{A^2} + 4B[\frac{1}{{{a_{\rm{k}}}}}({p_{\rm{e}}}{{\rm{e}}^{{a_{\rm{k}}}{p_{\rm{e}}}}} - 0.1 \cdot {{\rm{e}}^{0.1{a_{\rm{k}}}}}) - \frac{1}{{{a_{\rm{k}}}^2}}({{\rm{e}}^{{a_{\rm{k}}}{p_{\rm{e}}}}} - {{\rm{e}}^{0.1{a_{\rm{k}}}}})]} - A}}{{2B}} $ | (27) |
同时考虑启动压力梯度和应力敏感时,联立式(10)和式(19)求解可得二项式产能方程
当取启动压力梯度为0.002 5 MPa/m、应力敏感系数为0.041 MPa-1,将测试数据用修正二项式产能方程进行拟合,得到的产能曲线如图 6所示。
| $ \begin{array}{l} \frac{1}{{{a_{\rm{k}}}}}[{p_{\rm{e}}} \cdot {{\rm{e}}^{{a_{\rm{k}}} \cdot {p_{\rm{e}}}}} - {p_{{\rm{wf}}}} \cdot {{\rm{e}}^{{a_{\rm{k}}} \cdot {p_{{\rm{wf}}}}}}] - \frac{1}{{{a_{\rm{k}}}^2}}[{{\rm{e}}^{{a_{\rm{k}}} \cdot {p_{\rm{e}}}}} - {{\rm{e}}^{{a_{\rm{k}}} \cdot {p_{{\rm{wf}}}}}}] - C \cdot {{\rm{e}}^{{a_{\rm{k}}} \cdot \bar p}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;A \cdot (\overline {{\mu _{\rm{g}}}} \bar Z)q + B \cdot (\overline {{\mu _{\rm{g}}}} \bar Z){q^2} \end{array} $ | (28) |
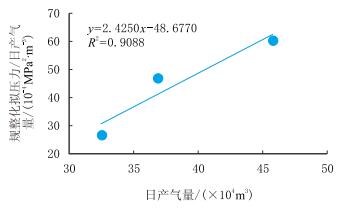 |
| 图6 同时考虑两个因素的二项式的产能方程 Fig. 6 The binomial productivity equation considering both of two factors |
经过拟合,得到同时考虑启动压力梯度和应力敏感的低渗气藏二项式产能方程(压力形式)
| $ \begin{array}{l} \frac{1}{{{a_{\rm{k}}}}}[{p_{\rm{e}}} \cdot {{\rm{e}}^{{a_{\rm{k}}} \cdot {p_{\rm{e}}}}} - {p_{{\rm{wf}}}} \cdot {{\rm{e}}^{{a_{\rm{k}}} \cdot {p_{{\rm{wf}}}}}}] - \\ \;\;\frac{1}{{{a_{\rm{k}}}^2}}[{{\rm{e}}^{{a_{\rm{k}}} \cdot {p_{\rm{e}}}}} - {{\rm{e}}^{{a_{\rm{k}}} \cdot {p_{{\rm{wf}}}}}}] - \\ \;\;\;\;\;\;C \cdot {{\rm{e}}^{{a_{\rm{k}}} \cdot \bar p}} = - 48.677{q_{{\rm{sc}}}} + 2.425{q_{{\rm{sc}}}}^2 \end{array} $ | (29) |
相关系数R2=0.908 8,进而可由式(29)求得考虑启动压力梯度为0.002 5 MPa/m、应力敏感系数为0.041 MPa-1时的无阻流量为97.42×104 m3/d。
| $ {q_{{\rm{AOF}}}} = \frac{{\sqrt {{A^2} + 4B[\frac{1}{{{a_{\rm{k}}}}}({p_{\rm{e}}}{{\rm{e}}^{{a_{\rm{k}}}{p_{\rm{e}}}}} - 0.1 \cdot {{\rm{e}}^{0.1{a_{\rm{k}}}}}) - \frac{1}{{{a_{\rm{k}}}^2}}({{\rm{e}}^{{a_{\rm{k}}}{p_{\rm{e}}}}} - {{\rm{e}}^{0.1{a_{\rm{k}}}}}) - C \cdot {{\rm{e}}^{{a_{\rm{k}}}\bar p}}]} - A}}{{2B}} $ | (30) |
比较以上两种产能方程(表 2),可以看出:在考虑启动压力梯度时,采用修正二项式产能方程计算出的无阻流量为155.89×104 m3/d,较常规二项式产能方程降低了9.44%;而在考虑应力敏感时,采用修正二项式产能方程计算出的无阻流量为111.76×104 m3/d,较常规二项式产能方程计算结果降低了35.08%;同时考虑两个因素影响时,采用修正二项式产能方程计算出的无阻流量为97.42×104 m3/d,较常规二项式产能方程计算结果降低了43.41%。由此可见,常规二项式产能方程由于未考虑低渗气藏应力敏感和启动压力梯度的影响,用其来计算低渗气藏气井的无阻流量与真实气井的无阻流量存在较大的偏差,这就会造成对气井产能的认识不准确,这样指导低渗气藏的生产势必会造成生产制度过大,递减加快等不利影响。
| 表2 常规与修正二项式产能方程对比 Table 2 The contrast of conventional and modified binomial productivity equations |
文中所述该水平井于2009年10月投入试采,初期日均产气量为29.4×104 m3,井口油压的压降速度为1.51 MPa/m,压降速度非常快,后期经过生产调整,通过试采动态及气藏工程论证认为其合理的产量在12~15×104 m3/d。而该地区的合理产量按经验为无阻流量的1/5~1/7,据此可判断采用修正二项式产能方程计算出来的无阻流量较常规二项式产能方程更为适用(表 3)。
| 表3 常规二项式方程与修正二项式方程的适用性对比 Table 3 The contrast of applicability between the conventional binomial equation and modified binomial equation |
从表 3可知:通过对川西某气藏岩芯实验得出的应力敏感系数和启动压力梯度,采用修正二项式产能方程计算出来的无阻流量更为合理,更能反映气藏的真实情况。只有全面地考虑储层的基本特征,才能“量体裁衣”,为气藏的合理开发提供科学可靠的依据。
4 结论(1) 基于拟稳定渗流理论,将启动压力梯度和应力敏感引入Forchheimer渗流方程,建立了低渗气藏水平井修正二项式产能方程。
(2) 以川西某低渗气藏气井实例说明,常规二项式产能方程计算无阻流量由于未考虑启动压力梯度和应力敏感的影响,计算值与笔者推导的修正二项式产能方程计算结果相差较大(高出了76.73%),可见在计算低渗气藏无阻流量时,应充分考虑启动压力梯度和应力敏感的影响。
(3) 通过对修正二项式产能方程适应性的探讨,认为采用修正二项式产能方程计算出来的无阻流量更为合理,更能反映气藏的真实情况。
| [1] |
冯朋鑫, 李进步, 陆利平, 等. 水平井技术在苏里格气田低渗气藏中的应用[J].
石油化工应用, 2010, 29 (8) : 37 –42.
Feng Pengxin, Li Jinbu, Lu Liping, et al. Implication of horizontal well technology in Sulige low permeability gas field[J]. Petrochemical Industry Application, 2010, 29 (8) : 37 –42. |
| [2] | 李建奇, 杨志伦, 陈启文, 等. 苏里格气田水平井开发技术[J]. 天然气工业, 2011, 31 (8) : 60 –64. |
| [3] |
李海平, 贾爱林, 何东博, 等. 中国石油的天然气开发技术进展及展望[J].
天然气工业, 2010, 30 (1) : 5 –7.
Li Haiping, Jia Ailin, He Dongbo, et al. Technical progress and outlook of natural gas development for the PetroChina[J]. Natural Gas Industry, 2010, 30 (1) : 5 –7. |
| [4] |
王华军, 胡涛, 李明, 等. 低渗透油气田水平井开发特点及影响分析[J].
石油化工应用, 2011, 30 (1) : 66 –68, 79.
Wang Huajun, Hu Tao, Li Ming, et al. Horizontal wells in low permeability oil and gas field development features and influencing factors[J]. Petrochemical Industry Application, 2011, 30 (1) : 66 –68, 79. |
| [5] | 陈作, 吴允. 四川水平井钻井技术的现状及发展方向[J]. 钻采工艺, 2003, 26 (4) : 1 –2. |
| [6] |
吴月先. 中国陆上油气水平井技术成效及新思考[J].
石油钻探技术, 2007, 35 (2) : 83 –86.
Wu Yuexian. Discussions about China onshore horizontal drilling technology[J]. Petroleum Drilling Techniques, 2007, 35 (2) : 83 –86. |
| [7] | 陈敏. 举足轻重的水平井技术[J]. 天然气工业, 2004, 24 (3) : 60 . |
| [8] |
荣宁, 吴迪, 韩易龙, 等. 双台阶水平井在塔里木盆地超深超薄边际油藏开发中的应用及效果评价[J].
天然气地球科学, 2006, 17 (2) : 230 –232.
Rong Ning, Wu Di, Han Yilong, et al. The application and effectiveness evaluation of double-step horizontal wells in super-deep and super-thin margin reservoir of tarim[J]. Natural Gas Geoscience, 2006, 17 (2) : 230 –232. |
| [9] |
孙来喜, 李成勇, 李成, 等. 低渗透气藏应力敏感与气井产量分析[J].
天然气工业, 2009, 29 (4) : 74 –76.
Sun Laixi, Li Chengyong, Li Cheng, et al. Stress sensitivity effect of low-permeability gas reservoirs and production analysis of gas wells[J]. Natural Gas Industry, 2009, 29 (4) : 74 –76. |
| [10] |
杨滨, 姜汉桥, 陈民锋, 等. 应力敏感气藏产能方程研究[J].
西南石油大学学报:自然科学版, 2008, 30 (5) : 158 –160.
Yang Bin, Jiang Hanqiao, Chen Minfeng, et al. Diliverability equation for stress-sensitive gas reservoir[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2008, 30 (5) : 158 –160. |
| [11] |
胥洪俊, 范明国, 康征, 等. 考虑渗透率应力敏感的低渗气藏产能预测公式[J].
天然气地球科学, 2008, 19 (1) : 145 –147.
Xu Hongjun, Fan Mingguo, Kang Zheng, et al. A productivity prediction equation considering rock permeability stress-sensitivity in low-permeability gas reservoirs[J]. Natural Gas Geoscience, 2008, 19 (1) : 145 –147. |
| [12] | 郑丽坤. 考虑渗透率应力敏感的气井无阻流量预测方法研究[J]. 石油地质与工程, 2010, 24 (2) : 101 –103. |
| [13] |
蒋艳芳, 张烈辉, 刘启国, 等. 应力敏感影响下低渗透气藏水平井产能分析[J].
天然气工业, 2011, 31 (10) : 54 –56.
Jiang Yanfang, Zhang Liehui, Liu Qiguo, et al. Productivity analysis of horizontal wells in low-permeability gas reservoirs considering stress sensitivity[J]. Natural Gas Industry, 2011, 31 (10) : 54 –56. |
| [14] |
孟令强, 黄炳光, 孟琦, 等. 考虑变启动压降的低渗气藏压裂井产能分析[J].
天然气勘探与开发, 2013, 36 (4) : 57 –60.
Meng Lingqiang, Huang Bingguang, Meng Qi, et al. Analysis on fractured-well productivity in lowpermeability gas reservoirs with consideration of variable strating pressure drop[J]. Natural Gas Exploration & Development, 2013, 36 (4) : 57 –60. |
| [15] |
李乐忠, 李相方, 何东博. 考虑变启动压降低渗气藏产能方程的建立[J].
油气井测试, 2010, 19 (1) : 5 –7.
Li Lezhong, Li Xiangfang, He Dongbo. The establishment of deliverability equation with consideration of variable threshold pressure drop in low permeability gas reservoir[J]. Well Testing, 2010, 19 (1) : 5 –7. |
| [16] |
郭晶晶, 张烈辉, 梁斌. 考虑启动压力梯度的低渗透气藏压裂井产能分析[J].
天然气工业, 2010, 30 (7) : 45 –47.
Guo Jingjing, Zhang Liehui, Liang Bin. Productivity analysis of a fractured well in low-permeability gas reservoirs considering threshold pressure gradient[J]. Natural Gas Industry, 2010, 30 (7) : 45 –47. |
| [17] | 张琰, 崔迎春. 砂砾性低渗气层压力敏感性的试验研究[J]. 石油钻采工艺, 1999, 21 (6) : 1 –6. |
| [18] |
宋传真, 郑荣臣. 致密低渗气藏储层应力敏感性及其对单井产能的影响[J].
大庆石油地质与开发, 2006, 25 (6) : 47 –49.
Song Chuanzhen, Zheng Rongchen. Stress sensitivity of low-permeability tight gas reservoir and its effect on single well productivity[J]. Petroleum Geology & Oilfield Development in Daqing, 2006, 25 (6) : 47 –49. |
| [19] |
罗瑞兰, 程林松, 彭建春, 等. 油气储层渗透率应力敏感性与启动压力梯度的关系[J].
西南石油学院学报, 2005, 27 (3) : 20 –22.
Luo Ruilan, Cheng Linsong, Peng Jianchun, et al. The relationship between stress-sensitivity permeability and starting pressure gradient of reservoir[J]. Journal of Southwest Petroleum Institute, 2005, 27 (3) : 20 –22. |
| [20] | 李士伦. 天然气工程. 北京:石油工业出版社[M]. 2000 . |
| [21] |
陈元千. 水平井产量公式的推导与对比[J].
新疆石油地质, 2008, 29 (1) : 68 –71.
Chen Yuanqian. Derivation and correlation of production rate formula for horizontal well[J]. Xinjiang Petorleum Geology, 2008, 29 (1) : 68 –71. |
| [22] | 马飞, 杨逸, 宋燕高, 等. 新场气田低品质储层启动压力梯度影响因素[J]. 石油地质与工程, 2011, 25 (2) : 72 –74. |
 2014, Vol. 36
2014, Vol. 36

