2. 中国石化集团国际石油勘探开发有限公司, 北京 朝阳 100029;
3. 中国石油大港油田勘探开发研究院, 天津 大港 300280
2. International Petroleum Exploration and Production Corporation, SINOPEC, Chaoyang, Beijing 100029, China;
3. Research Institute of Exploration and Development, Dagang Oil Field, PetroChina, Dagang, Tianjin 300280, China
致密火山岩储层由于微观孔隙结构复杂、非均质性强、有效砂体连通性差等特点,其渗流机理与常规储层有明显不同。针对致密火山岩气藏储层物性差,基质泄气半径小,无自然产能或自然产能低,开发难度大等特征,国内外目前普遍使用“长井段水平井加体积压裂”的开发技术,从而实现致密火山岩气藏的有效开发。
国内学者在引入和借鉴国外相关理论技术的同时,针对国内油气藏水平井压裂的实际情况,结合油气藏具体的渗流特征,推导出了许多压裂水平井的产能方程[1-9]。综合来看,国内水平井压裂产能公式研究存在着气藏渗流特征相似、气藏模型条件简单化和省略等问题,同时公式推导大多应用保角变换方法、复位势理论等,求解方法传统单一,缺少新的思路,大多未能考虑到致密火山岩储层渗流的特殊性和复杂性,从而不能准确反映气体在“长井段水平井加体积压裂”改造模式下的实际流动状况。
本文针对致密火山岩气藏渗流特征,在压裂水平井稳态渗流的基础上引入了基质泄气半径的非瞬态模型,考虑致密火山岩储层各影响因素对体积压裂水平井产能的影响,同时引入当量井径模型,将单条裂缝的压力分布方程等效为同等条件下的直井压力分布方程,从而得到多级压裂水平井的非稳态产能模型。最近,将现场油气田的实际数据应用于该产能模型中,并对产能模型的影响因素进行了单参数敏感性分析。
1 水平井压裂后产能预测模型在一个水平、无限大、均质和等厚的致密火山岩气藏中,存在一口压裂水平井,该水平井的完井方式为射孔完井。现作出如下假设: (1)气体在储层中的渗流为等温非稳态渗流,不考虑重力对气体渗流的影响;(2)压裂裂缝能够完全有效沟通储层;(3)裂缝与水平井筒垂直,且与井眼对称等间距排列;(4)气体首先沿裂缝面流入裂缝,再由裂缝流到水平井井筒,而不直接流入井筒;(5)裂缝间存在相互干扰现象,不考虑水平井筒内的压力损失;(6)忽略裂缝壁面污染造成的影响。
气体在致密火山岩储层中的渗流可以划分成以下3个阶段:气藏-裂缝的椭圆型渗流、裂缝-近井筒的线性渗流和裂缝-井筒的径向渗流。由于不同渗流阶段的渗流区域、渗流机理及渗流介质都具有巨大差异,因此需要分别考虑不同生产阶段的渗流特性及产能影响因素,并建立起各个生产阶段相对应的产能方程。
1.1 气藏-裂缝渗流模型 1.1.1 稳态渗流模型气体在储层渗流过程中,由于非线性渗流机理的存在,气体的流动并非呈线性流,而表现为非达西渗流。
当气井经过人工压裂生产后,气体的渗流模型发生了变化,流动变为拟径向流。在人工压裂裂缝的改造作用下,气体在储层渗流模式为二维椭圆渗流,该共轭等压椭圆以裂缝端点为焦点。其直角坐标与椭圆坐标相互关系为
| $ \left\{ {\begin{array}{*{20}{l}} {x = A\cos \eta }\\ {y = B\sin \eta } \end{array}} \right. $ | (1) |
| $ \left\{ {\begin{array}{*{20}{l}} {A = {x_{\rm{F}}}\cosh \xi }\\ {B = {x_{\rm{F}}}\sinh \xi } \end{array}} \right. $ | (2) |
由式(1)和式(2)可以得到等压椭圆族和双曲线流线族方程如下
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{ }}{x^2}}}{{{\rm{ }}{A^2}}} + \frac{{{\rm{ }}{y^2}}}{{{\rm{ }}{B^2}}} = 1}\\ {\frac{{{x^2}}}{{{{({x_{\rm{F}}}\cos \eta )}^2}}} - \frac{{{y^2}}}{{{{({x_{\rm{F}}}\sin \eta )}^2}}} = 1} \end{array}} \right. $ | (3) |
等压椭圆族可以用发展的矩形族来描述
| $ \left\{ {\begin{array}{*{20}{l}} {\bar x = {x_{\rm{F}}}\cosh \xi }\\ {\bar y = \frac{2}{{\rm{\pi }}}\int_0^{\frac{{\rm{\pi }}}{2}} {B\sin \eta {\rm{d}}\eta } = \frac{{2{x_{\rm{F}}}}}{{\rm{\pi }}}\sinh \xi } \end{array}} \right. $ | (4) |
式中:
x,y-直角坐标,m;
A,B-椭圆的长轴和短轴,m;
$\xi$,$\eta$-椭圆坐标,m;
$x_{\rm{F}}$-裂缝的半长,m;
$\overline x$,$\overline y$-发展的矩形族坐标,m。
气体在基质孔隙内渗流时,考虑到启动压力梯度、应力敏感效应[10]及滑脱效应[11],致密火山岩气体渗流数学模型由以下基本方程组成
广义达西公式
| $ {v_{\rm{m}}} = \frac{K}{\mu }(\frac{{{\rm{d}}p}}{{{\rm{d}}\bar y}} - \lambda ) $ | (5) |
应力敏感方程
| $ K = {K_{{\rm{m}}0}}{{\rm{e}}^{ - \alpha ({p_{\rm{i}}} - p)}} $ | (6) |
滑脱效应方程
| $ {K_{\rm{g}}} = K\left( {1 + \frac{b}{{\bar p}}} \right) $ | (7) |
其中
| $ \frac{{{\rm{d}}p}}{{{\rm{d}}\bar y}} = \frac{{{\rm{d}}p}}{{{\rm{d}}\xi }} \cdot \frac{{{\rm{d}}\xi }}{{{\rm{d}}y}} = \frac{{\rm{\pi }}}{{2{x_{\rm{F}}}\cosh \xi }} \cdot \frac{{{\rm{d}}p}}{{{\rm{d}}\xi }} $ | (8) |
式中:
${v_{\rm{m}}}$-拟径向流的渗流速度,m/s;
${K}$-基质的渗透率,mD;
$\mu$-气体黏度,mPa·s;
p-裂缝两端的压力,MPa;
$\lambda$-启动压力梯度,MPa/m;
${K_{{\rm{m}}0}}$-基质的初始渗透率,mD;
$\alpha$-应力敏感系数,MPa-1;
$p_{\rm{i}}$-原始地层压力,MPa;
${K_{\rm{g}}}$-气测渗透率,mD;
b-气体滑脱因子,MPa;
$\overline p$-气藏平均压力,MPa。
在y方向椭圆柱过流断面的流量为
| $ q = \frac{{45{\rm{\pi }}a}}{{32}}h \cdot {v_{\rm{m}}} $ | (9) |
式中:q-产量,m3/s;
h-油层厚度,m。
将式(6)~式(9)代入到式(5)中,得
| $ \begin{array}{l} \frac{{{K_{{\rm{m}}0}}{{\rm{e}}^{ - \alpha ({p_{\rm{i}}} - p)}}}}{\mu } \cdot 1 + \frac{b}{{\bar p}} \cdot (\frac{{\rm{\pi }}}{{2{x_{\rm{F}}}\cosh \xi }} \cdot \frac{{{\rm{d}}p}}{{{\rm{d}}\xi }} - \lambda ) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{ZT}}{p}\frac{{{p_{{\rm{sc}}}}}}{{{Z_{{\rm{sc}}}}{T_{{\rm{sc}}}}}}\frac{{32{q_{{\rm{sc}}}}}}{{45{\rm{\pi }}{x_{\rm{F}}}h\cosh \xi }} \end{array} $ | (10) |
令
| $ \begin{array}{l} m({p_{\rm{i}}}) - m(p) = \frac{{64{p_{{\rm{sc}}}}T \cdot \int_{\xi (0)}^{\xi ({R_{\rm{e}}})} {{\rm{d}}\xi } }}{{45{{\rm{\pi }}^2}{K_{{\rm{m0}}}}{Z_{{\rm{sc}}}}{T_{{\rm{sc}}}}(1 + b/\bar p)h}} \cdot {q_{{\rm{sc}}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{2{x_{\rm{F}}}}}{{\rm{\pi }}}\int_{\xi (0)}^{\xi ({R_{\rm{e}}})} {\lambda f(\bar p)\cosh \xi {\rm{d}}\xi } \end{array} $ | (11) |
式中:
Z-气体压缩因子,无因次;
T-气藏温度,K,1 ℃=273.15 K;
$p_{{\rm{sc}}}$-标准大气压力,MPa;
$Z_{{\rm{sc}}}$-标准状态下的气体压缩因子,无因次;
$T_{{\rm{sc}}}$-标准状态下的气藏温度,K;
$q_{{\rm{sc}}}$-在标准状况下的气体产量,m3/d;
$p_0$-起始压力,MPa;
$\sigma$-方程变量;
${R_{\rm{e}}}$-外边界,m。
1.1.2 基质泄气半径非瞬态模型致密火山岩气藏基质的泄气半径具有非瞬态效应,会随着压力波的传播而不断扩张。实际上在每一瞬间气体流动的整个区域实际上涉及了整个地层,可以将气藏整个区域分成两个区:受压力激动区和未激动区。随着时间的增加激动区半径(即基质的泄气半径)不断增大[12]。激动区和未激动区动界面的运动规律可以借助于物质平衡方程和边界条件求出。
经过保角变换作用,
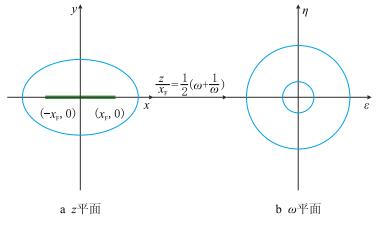 |
| 图1 保角变换示意图 Fig. 1 Schematic of conformal transformation |
为了求R(t),建立了一个物质平衡方程。在半径为R(t)的区域内,原始天然气储量为
| $ {M_0} = {\rm{ \pi }}[{R^2}(t) - r_{\rm{w}}^2]h\phi \frac{{{\rho _{{\rm{aT}}}}}}{{{p_{{\rm{aT}}}}}}{p_{\rm{a}}} $ | (12) |
式中:
${M_0}$-初始气藏含气量,kg;
R(t)-基质的动用半径,m;
$r_{\rm{w}}$-气井的半径,m;
$\phi$-孔隙度,%;
$\rho _{{\rm{aT}}}$-气体在标况下的密度,kg/m3;
$p_{{\rm{aT}}}$-标准大气压,MPa;
${p_{\rm{a}}}$-实际地层压力,MPa。
目前储量用平均压力$\overline p $表示
| $ {M_{\rm{t}}} = {\rm{ \pi }}[{R^2}(t) - r_{\rm{w}}^{\rm{2}}]h\phi \frac{{{\rho _{{\rm{aT}}}}}}{{{p_{{\rm{aT}}}}}}\bar p $ | (13) |
| $ \bar p = {p_{\rm{i}}} - \frac{{p_{\rm{i}}^2 - p_{{\rm{wf}}}^2}}{{4{p_{\rm{i}}}\ln [R(t)/{r_{\rm{w}}}]}} $ | (14) |
由于井以固定产量QaT采气,所以到瞬间t为止,采出的天然气的质量等于ρaTQaTt,因而
| $ {M_0} - {M_{\rm{t}}} = {\rho _{{\rm{aT}}}}{Q_{{\rm{aT}}}}t $ | (15) |
考虑了启动压力梯度的致密火山岩稳定渗流的产量方程为
| $ {Q_{{\rm{aT}}}} = \frac{{{\rm{\pi }}Kh\left\{ {p_{\rm{i}}^2 - p_{{\rm{wf}}}^2 - \lambda \bar p\left[{R(t) - {r_{\rm{w}}}} \right]} \right\}}}{{\mu {p_{{\rm{aT}}}}\ln [R(t)/{r_{\rm{w}}}]}} $ | (16) |
把加权平均压力$\overline p $的表达式(14)和产量公式(16)代入到式(18),得
| $ {R^2}(t) - r_{\rm{w}}^{\rm{2}} = \frac{{4K{p_{\rm{i}}}}}{{\mu \phi }} \cdot \frac{{p_{\rm{i}}^2 - p_{{\rm{wf}}}^{\rm{2}}}}{{\lambda \bar p[R(t) - {r_{\rm{w}}}]}}t $ | (17) |
考虑到气体渗流的应力敏感效应,得到下列R(t){~}t的关系式
| $ {R^2}(t) - r_{\rm{w}}^2 = \frac{{4{K_{{\rm{m0}}}}{{\rm{e}}^{ - \alpha ({p_{\rm{i}}} - \bar p)}}{p_{\rm{i}}}}}{{\mu \phi }}\frac{{(p_{\rm{i}}^2 - p_{{\rm{wf}}}^{\rm{2}}) - \lambda \bar p[R(t) - {r_{\rm{w}}}]}}{{p_{\rm{i}}^2 - p_{{\rm{wf}}}^2}}t $ | (18) |
其中,
| $ {{\rm{e}}^{2{\xi _{\rm{e}}}(t)}} - 1 = \frac{{4{K_{{\rm{m}}0}}{{\rm{e}}^{ - \alpha ({p_i} - \bar p)}}{p_{\rm{i}}}}}{{\mu \phi }}\frac{{(p_{\rm{i}}^2 - p_{{\rm{wf}}}^2) - \lambda \bar p[{{\rm{e}}^{{\xi _{\rm{e}}}(t)}} - 1]}}{{p_{\rm{i}}^2 - p_{{\rm{wf}}}^2}}t $ | (19) |
| $ \bar p = {p_{\rm{i}}} - \frac{{p_{\rm{i}}^2 - p_{{\rm{wf}}}^2}}{{4{p_{\rm{i}}}{\xi _{\rm{e}}}(t)}} $ | (20) |
将式(19)~式(20)代入到式(11)中,得到基质到裂缝椭圆形不稳定渗流的产能模型
| $ \begin{array}{l} m({p_{\rm{i}}}) - m(p) = \frac{{64{p_{{\rm{sc}}}}T \cdot \int_0^{{\xi _{\rm{e}}}(t)} {{\rm{d}}\xi } }}{{45{{\rm{\pi }}^2}{K_{{\rm{m0}}}}{Z_{{\rm{sc}}}}{T_{{\rm{sc}}}}(1 + b/\bar p)h}} \cdot {q_{{\rm{sc}}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{2{x_{\rm{F}}}}}{{\rm{\pi }}}\int_0^{{\xi _{\rm{e}}}(t)} {\lambda f(\bar p)\cosh \xi {\rm{d}}\xi } \end{array} $ | (21) |
式中:
1.1.3 压裂水平井非稳态渗流模型在压裂水平井基质的稳态渗流方程中引入基质泄气半径的非瞬态模型,即可得到压裂水平井非稳态的渗流模型。
将式(12)~式(15)代入式(14),即可得到拟压力随时间变化的公式,得
| $ \begin{array}{l} ({p_{\rm{i}}}) - m(p) = \frac{{64{p_{{\rm{sc}}}}T \cdot {\xi _{\rm{e}}}(t)}}{{45{{\rm{\pi }}^2}{K_{{\rm{m}}0}}{Z_{{\rm{sc}}}}{T_{{\rm{sc}}}}(1 + b/\bar p)h}} \cdot {q_{{\rm{sc1}}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{2{x_{\rm{F}}}}}{{\rm{\pi }}}\int_0^{{\xi _{\rm{e}}}(t)} {\lambda f(\bar p)\cosh \xi {\rm{d}}\xi } \end{array} $ | (22) |
假设在气藏-裂缝中气体的流量为qsc1(折算到地面标准状况下),在裂缝尖端的压力为p1, 拟压力为m(p1),即得到气藏-裂缝的非稳态渗流的拟压力分布方程
| $ \begin{array}{l} ({p_{\rm{i}}}) - m({p_1}) = \frac{{64{p_{{\rm{sc}}}}T \cdot {\xi _{\rm{e}}}(t)}}{{45{{\rm{\pi }}^2}{K_{{\rm{m}}0}}{Z_{{\rm{sc}}}}{T_{{\rm{sc}}}}(1 + b/\bar p)h}} \cdot {q_{{\rm{sc1}}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{2{x_{\rm{F}}}}}{{\rm{\pi }}}\int_0^{{\xi _{\rm{e}}}(t)} {\lambda f(\bar p)\cosh \xi {\rm{d}}\xi } \end{array} $ | (23) |
式中:
${M_{\rm{t}}}$-此时气藏含气量,kg;
$p_{{\rm{wf}}}$-井底流压,MPa;
${Q_{{\rm{aT}}}}$-产气量,m3/d;
$q_{\rm{sc1}}$-气藏-裂缝中气体的流量,m3/d。
1.2 裂缝-近井筒渗流模型裂缝-近井筒渗流中,流动介质为压裂裂缝。裂缝渗透率高,气体在裂缝内的流速大,此时达西公式已不再适用,需采用Forchheimer二项式产能方程[13]来描述气体流动。综合考虑了高速紊流效应、应力敏感效应以及滑脱效应,致密火山岩气藏的渗流模型由以下几个方程组成
高速紊流方程
| $ \frac{{{\rm{d}}p}}{{{\rm{d}}x}} = \frac{\mu }{{{K_{\rm{F}}}}}{v_{\rm{F}}} + {\beta _{\rm{g}}}{\rho _{\rm{g}}}v_{\rm{F}}^2 $ | (24) |
应力敏感方程
| $ {K_{\rm{F}}} = {K_{{\rm{F}}0}}{{\rm{e}}^{ - \alpha ({p_{\rm{i}}} - p)}} $ | (25) |
则气体在裂缝中渗流速度为
| $ {v_{\rm{F}}} = \frac{{{q_2}}}{{2{w_{\rm{F}}}h}} = \frac{Z}{p} \cdot \frac{{{p_{{\rm{sc}}}}T}}{{{Z_{{\rm{sc}}}}{T_{{\rm{sc}}}}}} \cdot \frac{{{q_{{\rm{sc2}}}}}}{{2{w_{\rm{F}}}h}} $ | (26) |
假设裂缝内线性流动区的流量为qsc2(折算到地面标准状况下),裂缝内线性流动区与径向流动区(半径为h/2)的交界面处的压力为p2,拟压力为m(p2),即得到气藏-近井筒的非稳态渗流的拟压力分布方程
| $ \begin{array}{l} m({p_1}) - m({p_2}) = \frac{{{p_{{\rm{sc}}}}T({x_{\rm{F}}} - h/2)}}{{2{K_{{\rm{F}}0}}{w_{\rm{F}}}h{Z_{{\rm{sc}}}}{T_{{\rm{sc}}}}}} \cdot {q_{{\rm{sc2}}}} + \\ \;\;\;\;\;\;\;\;\;\;{\beta _{\rm{g}}}\frac{{MTZp_{{\rm{sc}}}^2({x_{\rm{F}}} - h/2)f(\bar p)}}{{4{\rm{R}}\bar pw_{\rm{F}}^2{h^2}Z_{{\rm{sc}}}^{\rm{2}}T_{{\rm{sc}}}^2}} \cdot q_{{\rm{sc}}2}^2 \end{array} $ | (27) |
其中
式中:$K_{\rm{F}}$-裂缝的渗透率,mD;
${v_{\rm{F}}}$-气体在裂缝中的渗流速度,m/s;
${\beta _{\rm{g}}}$-气体的紊流系数,m-1,
${\rho _{\rm{g}}}$-气体的密度,g/cm3;
${K_{{\rm{F}}0}}$-裂缝的初始渗透率,mD;
$q_2$-裂缝内线性流动区的流量(地下),m3/d;
$q_{{\rm{sc2}}}$-裂缝内线性流动区的流量,m3/d;
${w_{\rm{F}}}$-裂缝的宽度,m;
$p_1$-裂缝尖端的压力,MPa;
$p_2$-裂缝内线性流动区与径向流动区(半径为h/2)的交界面处的压力,MPa;
M-气体分子量,kg/Kmol;
R-气体常数,R=8.314 J/(mol·K)。
1.3 裂缝-井筒径向渗流模型气体从裂缝内沿着裂缝面向水平井筒渗流时,在近井筒周围由于径向流的存在而产生了一个附加的压力降,如图 2所示,该现象即所谓的聚流效应[14]。
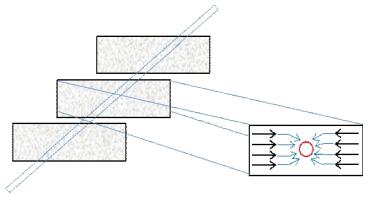 |
| 图2 裂缝–井筒附近的径向流 Fig. 2 Schematic of radial flow near fissure-wellbore |
假设裂缝内径向流动区的流量为qsc3(折算到地面标准状况下),则径向流的流速为
| $ v = \frac{{{q_3}}}{{2{\rm{\pi }}r{w_{\rm{F}}}}} = \frac{Z}{p} \cdot \frac{{{p_{{\rm{sc}}}}T}}{{{Z_{{\rm{sc}}}}{T_{{\rm{sc}}}}}} \cdot \frac{{{q_{{\rm{sc}}3}}}}{{2{\rm{\pi }}r{w_{\rm{F}}}}} $ | (28) |
式中:v-气体沿裂缝内径向流的流速,m/s;
$q_3$-裂缝内径向流动区的流量(地下),m3/d;
r-径向流的半径,m;
$q_{{\rm{sc}}3}$-裂缝内径向流动区的流量(地面),m3/d。
将式(24)、式(25)和式(28)代入到式(23)中,即得裂缝-井筒非稳态流的拟压力方程
| $ \begin{array}{l} m({p_2}) - m({p_{{\rm{wf}}}}) = \frac{{{p_{{\rm{sc}}}}T\ln (h/2{r_{\rm{w}}})}}{{2{\rm{\pi }}{K_{{\rm{F}}0}}{w_{\rm{F}}}{Z_{{\rm{sc}}}}{T_{{\rm{sc}}}}}} \cdot {q_{{\rm{sc}}3}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\beta _{\rm{g}}}\frac{{MTZ(1/{r_{\rm{w}}} - 2/h)p_{{\rm{sc}}}^2}}{{4{{\rm{\pi }}^2}{\rm{R}}\bar pZ_{{\rm{sc}}}^{\rm{2}}T_{{\rm{sc}}}^{\rm{2}}w_{\rm{F}}^2}} \cdot q_{{\rm{sc}}3}^2 \end{array} $ | (29) |
其中
水平井经过人工压裂后,其渗流场可以划分为两个部分:内部渗流场(裂缝-水平井筒)与外部渗流场(储层-裂缝),由于内外渗流场之间通过串联来供气,根据水电相似原理,得到q1=q2=q3,同时内外渗流场之间的接触面压力相等。将式(23)、式(27)、式(29)联立,得考虑滑脱效应、应力敏感效应、启动压力梯度和高速非达西紊流效应下的单条缝产能公式
| $ \begin{array}{l} m({p_{\rm{i}}}) - m({p_{{\rm{wf}}}}) = \frac{{2{x_{\rm{F}}}}}{{\rm{\pi }}}\int_0^{{\xi _{\rm{e}}}(t)} {\lambda f(\bar p)\cosh \xi {\rm{d}}\xi } + \\ \frac{{{p_{{\rm{sc}}}}T}}{{{Z_{{\rm{sc}}}}{T_{{\rm{sc}}}}}}\left[{\frac{{64{\xi _{\rm{e}}}(t)}}{{45{{\rm{\pi }}^2}{K_{{\rm{m}}0}}\left( {(1 + b/\bar p)} \right)h}} + \frac{{{x_{\rm{F}}} - h/2}}{{2{K_{{\rm{F}}0}}{w_{\rm{F}}}h}} + \frac{{\ln (h/2{r_{\rm{w}}})}}{{2{\rm{\pi }}{K_{{\rm{F}}0}}{w_{\rm{F}}}}}} \right] \cdot {q_{{\rm{sc}}}} + \\ \;\;\;\;\;\;\;\;\;{\beta _{\rm{g}}}\frac{{MTZp_{{\rm{sc}}}^2}}{{4R\bar pw_{\rm{F}}^2Z_{{\rm{sc}}}^2T_{{\rm{sc}}}^2}}[\frac{{({x_{\rm{F}}} - h/2)f(\bar p)}}{{{h^2}}} + \frac{{(1/{r_{\rm{w}}} - 2/h)}}{{{{\rm{\pi }}^2}}}] \cdot q_{{\rm{sc}}}^2 \end{array} $ | (30) |
当得到在某一复杂条件下某一口复杂井的产能公式时,可以使之与常规达西渗流条件下的普通直井进行类比,此时即可得到相应的普通直井的产能公式。因此,将式(30)与广义达西渗流条件下考虑启动压力梯度、应力敏感效应及滑脱效应的普通直井产能方程对比,可以得到横向压裂水平井单条裂缝的当量井径requ[15]。
根据广义达西方程、应力敏感及滑脱效应方程获得普通直井的压力分布方程
| $ m({p_{\rm{i}}}) - m(p) = \frac{{{p_{{\rm{sc}}}}T\ln ({R_{\rm{e}}}/r) \cdot {q_{{\rm{sc}}}}}}{{2{\rm{\pi }}{K_{{\rm{F}}0}}{Z_{{\rm{sc}}}}{T_{{\rm{sc}}}}(1 + b/\bar p)h}} + \lambda f(\bar p)({R_{\rm{e}}} - r) $ | (31) |
普通直井产能为
| $ m({p_{\rm{i}}}) - m({p_{{\rm{wf}}}}) = \frac{{{p_{{\rm{sc}}}}T\ln ({R_{\rm{e}}}/{r_{{\rm{equ}}}}) \cdot {q_{{\rm{sc}}}}}}{{2{\rm{\pi }}{K_{{\rm{F}}0}}{Z_{{\rm{sc}}}}{T_{{\rm{sc}}}}(1 + b/\bar p)h}} + \lambda f(\bar p)({R_{\rm{e}}} - {r_{{\rm{equ}}}}) $ | (32) |
联立式(30)、(32),获得横向压裂时水平井单条缝当量井径requ。
1.6 多级压裂水平井的产能模型压裂水平井有n条横向裂缝,不同裂缝间存在相互干扰,且裂缝位置不同影响程度不同。
根据拟压力降的叠加理论,运用当量井径模型,将多裂缝水平井等效为多口直井,从而将多裂缝水平井渗流转变为多口直井的叠加。根据拟压力叠加原理,得到各裂缝在第j条缝处的拟压力为
| $ \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} m({p_{\rm{i}}}) - m({p_{{\rm{wf}}1}}) = \Delta m{(p)_{11}}\left( {{q_{{\rm{sc}}1}}} \right) + \Delta m{(p)_{21}}\left( {{q_{{\rm{sc}}2}}} \right) + \Delta m{(p)_{31}}\left( {{q_{{\rm{sc}}3}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdots + \Delta m{(p)_{n1}}\left( {{q_{{\rm{sc}}n}}} \right) \end{array}\\ \begin{array}{l} m({p_{\rm{i}}}) - m({p_{{\rm{wf}}2}}) = \Delta m{(p)_{12}}\left( {{q_{{\rm{sc}}1}}} \right) + \Delta m{(p)_{22}}\left( {{q_{{\rm{sc}}2}}} \right) + \Delta m{(p)_{32}}\left( {{q_{{\rm{sc}}3}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdots + \Delta m{(p)_{n2}}\left( {{q_{{\rm{sc}}n}}} \right) \end{array}\\ \begin{array}{l} m({p_{\rm{i}}}) - m({p_{{\rm{wf}}3}}) = \Delta m{(p)_{13}}\left( {{q_{{\rm{sc}}1}}} \right) + \Delta m{(p)_{23}}\left( {{q_{{\rm{sc}}2}}} \right) + \Delta m{(p)_{33}}\left( {{q_{{\rm{sc}}3}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdots + \Delta m{(p)_{n3}}\left( {{q_{{\rm{sc}}n}}} \right) \end{array}\\ {\;\;\;\;\;\;\; \vdots }\\ \begin{array}{l} m({p_{\rm{i}}}) - m({p_{{\rm{wf}}n}}) = \Delta m{(p)_{1n}}\left( {{q_{{\rm{sc}}1}}} \right) + \Delta m{(p)_{2n}}\left( {{q_{{\rm{sc}}2}}} \right) + \Delta m{(p)_{3n}}\left( {{q_{{\rm{sc}}3}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdots + \Delta m{(p)_{nn}}\left( {{q_{{\rm{sc}}n}}} \right) \end{array} \end{array}} \right. $ | (33) |
假设气体在水平井筒内的渗流为无限导流,水平井筒内的压力均相等,则
| $ m({p_{{\rm{wf}}1}}) = m({p_{{\rm{wf}}2}}) = ... = m({p_{{\rm{wf}}n}}) $ | (34) |
压裂水平井产量为
| $ {q_{{\rm{sc}}}} = {q_{{\rm{sc}}1}} + {q_{{\rm{sc2}}}} + ... + {q_{{\rm{sc}}i}} = \sum\limits_{i = 1}^n {{q_{{\rm{sc}}i}}} $ | (35) |
联立式(33)~式(35),即可求得qsc~t的关系。
2 多级压裂水平井的产能特征及单参数敏感性分析受压裂技术和井下工具等条件的限制,目前我国致密火山岩气藏多级分段压裂水平井开发还处于初期阶段,开发井次还不多。本文选用吉林油田某致密火山岩气藏压裂效果较好的水平井参数作为基本参数。基础资料见表 1。
| 表1 吉林某气田基本参数 Table 1 Fundamental parameters of a gas field in Jilin Oilfield |
图 3考虑了启动压力梯度、应力敏感效应和滑脱效应时的ξe(t)随时间变化曲线,它同时表征了压力波向外传播情况。可以看出,生产初期地层渗透率很低,基质向裂缝渗流阻力大,供给慢,压力波向外传播的速度快;中后期基质的泄气范围逐渐增大,压力波向外传播速度逐渐减小并趋于稳定。
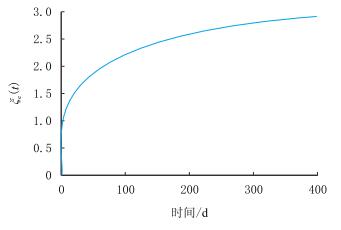 |
| 图3 ξe(t)随时间的关系 Fig. 3 Correlation between ξe(t) with time |
产能计算结果表明,启动压力梯度效应、滑脱效应及应力敏感效应对气井的产能影响程度比较大,因此在进行致密火山岩气藏产能评价时,需要考虑以上因素的影响。
不同参数对压裂水平井产能的影响作用如图 4所示。从图中可以看出,综合考虑了启动压力梯度、滑脱和应力敏感效应的气井,在开采初期阶段,由于仅裂缝附近的气体参与供气,故气井的产量较高。但由于气藏致密,渗流阻力大,导致了初期气井产量递减快。开采后期压力波逐渐向外扩散,从而基质的泄气面积增大,此时由气藏基质向井筒供气,由于基质的渗透率小,因此产量较低且递减慢。
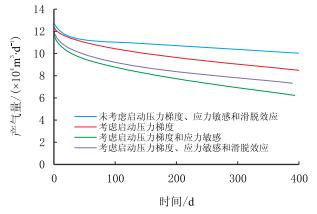 |
| 图4 不同产能计算结果对比图 Fig. 4 Comparison diagram of productivity |
启动压力梯度对压裂水平井产能的影响如图 5所示。启动压力梯度越大,对压裂水平井产能的影响程度也就越大。但是启动压力梯度对压裂水平井的影响存在一个拐点,当小于0.015 MPa/m时,其对产能的影响很小;当大于0.015 MPa/m时,其对产能的影响非常显著,在气藏开发过程中该因素不可忽略。
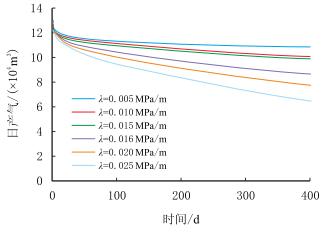 |
| 图5 启动压力梯度效应对气井产能的影响 Fig. 5 Influence of threshold gradient pressure on well productivity |
由于致密火山岩储层孔喉细小,因此介质渗流能力受压力影响明显,介质变形对气藏物性参数影响较大。
由图 6可知,随变形系数的增加,压裂水平井日产气量将逐渐减小。应力敏感系数$\alpha$越大,对产量的影响逐渐减小。当应力敏感系数$\alpha$小于0.15 MPa-1}时,对压裂水平井产量影响较大,而当其大于0.15 MPa-1时,对压裂水平井产量的影响很小。同时,应力敏感系数的大小仅影响日产量的相对高低,没有改变产量递减的变化趋势。
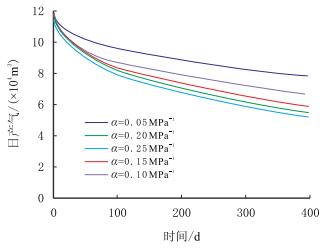 |
| 图6 应力敏感对压裂气井产能的影响 Fig. 6 Influence of stress sensitivity on well productivity |
由于致密火山岩孔隙喉道细小,气体在小孔道中流动时,气体壁面处流动速度不为零,当气体分子的平均自由程接近孔隙尺寸时,介质壁面处各分子将处于运动状态。
从图 7可以看出,随着滑脱系数b的增大,压裂水平井的日产气量逐渐增大,且增加趋势愈接近平缓。当滑脱系数b大于5 MPa后,滑脱效应对压裂水平井产能几乎没有影响。与启动压力梯度效应和应力敏感效应相比,滑脱效应对多级压裂水平井产能的影响程度较小。
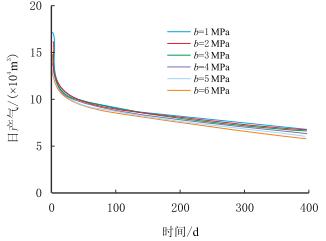 |
| 图7 滑脱效应对气井产能的影响 Fig. 7 Influence of klinkenberg effect on well productivity |
图 8为生产400 d时累计产气量和水平井长度之间的关系。从图中可以看出,气井产量和水平段长度并不满足线性关系。
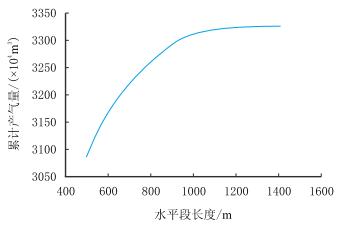 |
| 图8 水平段长度对气井产能的影响 Fig. 8 Influence of single well length on well productivity |
当水平段长度较短时,水平段长度的增加对气井产量的增加具有很大的贡献作用。当水平段长度突破一定值后,气井产量增加将变得缓慢。通过分析认为,随着水平井筒长度的增加,气体在井筒的流动距离增加,从而因为摩擦阻力引起的压力损失增加;同时,水平段增加,裂缝间距变宽,裂缝对产气量的贡献也随之减弱。因此水平井井筒长度存在一个最优的范围,该实例计算的最优范围为1 000~1 200 m。
2.2.5 压裂裂缝间距从图 9可以看出,裂缝间距越小,水平井产量越高。随着裂缝间距的逐渐减小,裂缝之间的干扰逐渐加强,从而致使产量增幅减小。
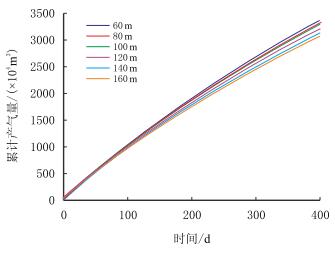 |
| 图9 裂缝间距对气井产能的影响 Fig. 9 Influence of fracture interval on well productivity |
该实例计算中,当裂缝间距小于100 m时,产量增加幅度将降低。因此,本例中最佳裂缝间距在100 m左右。
2.2.6 压裂裂缝长度从图 10可以看出,随着缝长的增加,水平井产量增加,这是因为人工裂缝有效沟通储层,改善储层渗透率,同时扩大了气井的泄气体积;但当缝长为一定值后,裂缝长度的增加,裂缝内阻力也将增大,从而导致产量增幅减小。
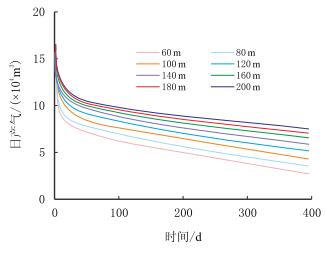 |
| 图10 裂缝长度对气井产能的影响 Fig. 10 Influence of fracture length on gas well productivity |
本实例中的气藏,当裂缝压裂裂缝半长大于180 m时,产量增加幅度明显降低。因此,本例中最佳裂缝间距在180 m左右。
3 结论(1)在综合考虑了启动压力梯度、滑脱效应及应力敏感效应等非线性渗流机理后,压裂水平井的生产规律表现为以下特征:生产初期产量高,递减很快,同时高产持续期较短;生产后期产量低,递减较慢,然后持续期较长,生产趋于稳定。
(2)在致密火山岩气藏开发过程中需要考虑启动压力梯度效应和应力敏感效应对气藏产能的影响。启动压力梯度和应力敏感对气井产量均起负作用。滑脱效应对压裂水平井产能影响不明显,可以忽略。
(3)水平段长度及压裂裂缝越长、裂缝间距越小,气井产量越高。但随裂缝长度的增加及裂缝间距的减小、水平段长度的增加,压裂水平井的产量增加幅度将会逐渐减小。因此对于具体的气藏,各个参数均存在一个最优范围。
| [1] |
郎兆新, 张丽华, 程林松. 压裂水平井产能研究[J].
石油大学学报:自然科学版, 1994, 18 (2) : 43 –46.
Lang Zhaoxin, Zhang Lihua, Cheng Linsong. Investigation on productivity of fractured horizontal well[J]. Journal of the University of Petroleum, China, 1994, 18 (2) : 43 –46. |
| [2] |
宁正福, 韩树刚, 程林松, 等. 低渗透油气藏压裂水平井产能计算方法[J].
石油学报, 2002, 23 (2) : 68 –71.
Ning Zhengfu, Han Shugang, Cheng Linsong, et al. Productivity calculation method of fractured horizontal wells in low permeability oil or gas field[J]. Acta Petrolei Sinica, 2002, 23 (2) : 68 –71. |
| [3] |
李廷礼, 李春兰, 吴英, 等. 低渗透油藏压裂水平井产能计算新方法[J].
中国石油大学学报:自然科学版, 2006, 30 (2) : 48 –52.
Li Tingli, Li Chunlan, Wu Ying, et al. A new way to calculate fractured horizontal wells productivity in low permeability oil reservoirs[J]. Journal of China University of Petroleum, 2006, 30 (2) : 48 –52. |
| [4] |
徐严波, 齐桃, 杨凤波, 等. 压裂后水平井产能预测新模型[J].
石油学报, 2006, 27 (1) : 89 –91.
Xu Yanbo, Qi Tao, Yang Fengbo, et al. New model for productivity test of horizontal well after hydraulic fracturing[J]. Acta Petrolei Sinica, 2006, 27 (1) : 89 –91. |
| [5] |
廉培庆, 同登科, 程林松, 等. 垂直压裂水平井非稳态条件下的产能分析[J].
中国石油大学学报:自然科学版, 2009, 33 (4) : 98 –102.
Lian Peiqing, Tong Dengke, Cheng Linsong, et al. Analysis of productivity in unsteady state of vertical fractured horizontal well[J]. Journal of China University of Petroleum, 2009, 33 (4) : 98 –102. |
| [6] |
范子菲, 方宏长, 牛新年. 裂缝性油藏水平井稳态解产能公式研究[J].
石油勘探与开发, 1996, 23 (3) : 52 –57.
Fan Zifei, Fang Hongchang, Niu Xinnian. A steady solution formula of horizontal well productivity in a fractured reservoirs[J]. Petroleum Exploration and Development, 1996, 23 (3) : 52 –57. |
| [7] |
曾凡辉, 郭建春, 尹建. 井筒与油藏耦合的压裂水平井非稳态产能计算模型[J].
现代地质, 2011, 25 (6) : 1159 –1166.
Zeng Fanhui, Guo Jianchun, Yin Jian. An unsteady state computation model of fractured horizontal well coupling with reservoir[J]. Geoscience, 2011, 25 (6) : 1159 –1166. |
| [8] |
朱维耀, 张玉广, 刘合, 等. 大庆敖南特低渗油层非达西渗流压裂水平井优化技术[J].
辽宁工程技术大学学报:自然科学版, 2009, 28 (S) : 123 –126.
Zhu Weiyao, Zhang Yuguang, Liu He, et al. Optimization method of hydraulic fracturing horizontal wells with extralow permeability in Daqing Aonan oil reservoirs[J]. Journal of Liaoning Technical University:Natural Science, 2009, 28 (S) : 123 –126. |
| [9] |
冯国庆, 刘启国, 石广志, 等. 考虑启动压力梯度的低渗透气藏不稳定渗流模型[J].
石油勘探与开发, 2008, 35 (4) : 457 –461.
Feng Guoqing, Liu Qiguo, Shi Guangzhi, et al. An unsteady seepage flow model considering kickoff pressure gradient for low-permeability gas reservoirs[J]. Petroleum Exploration and Development, 2008, 35 (4) : 457 –461. DOI:10.1016/S1876-3804(08)60094-4 |
| [10] | Klinkenberr L J. The permeability of porous media to liquids and gases[J]. API Drilling and Production Practice, 1941 (2) : 200 –213. |
| [11] | 黄炳光, 刘蜀知. 实用油藏工程与动态分析方法[M]. 北京: 石油工业出版社, 1998 : 190 -203. |
| [12] | 巴斯宁耶夫K C, 费拉索夫A M. 地下流体力学[M]. 北京: 石油工业出版社, 1992 : 189 -195. |
| [13] | 郭平, 张茂林, 黄全华, 等. 低渗透致密砂岩气藏开发机理研究[M]. 北京: 石油工业出版社, 2009 : 69 -70. |
| [14] | Klinkenberr L J. The permeability of porous media to liquids and gases[J]. API Drilling and Production Practice, 1941 (2) : 200 –213. |
| [15] | Nura, Yilmazo. Pore pressure fronts in fractured rock systems[D]. Stanford:Department of Geophysics, Stanford University, 1985. http://www.oalib.com/references/17521470 |
 2014, Vol. 36
2014, Vol. 36

