2. 中国石化中原油田勘探开发科学研究院, 河南 濮阳 457001
2. Exploration and Development Scientific Research Institute, Zhongyuan Oilfield, SINOPEC, Puyang, Henan 457001, China
有水气藏动态预测和气井见水时间预测是气藏开发技术调整及控水、治水措施实施的前期基础工作,也是气藏高效开发的重要保障。国内外大量学者基于多孔介质中流体质点的渗流规律等方法[1-6],推导出了有水气藏见水时间的计算公式;Sun H、熊健、孙贺东等基于渗流理论和物质平衡原理建立了气藏动态预测模型[7-10]。但是尚未见考虑边水水侵预警的动态预测方法。本文在前人研究基础上,基于体积平衡原理、以边水气藏水侵圆环为研究对象[11-13],再建立边水气藏水侵预警方程后,进一步结合产量预测、压力预测和水侵量预测模型,建立了一种新的基于水侵预警的边水气藏动态预测模型,并就PG气田开展了实例计算。
1 水侵预警方程的建立假定一个圆形、存在边水的气藏中,当从气藏采出一定气量之后,气藏的压力从原始地层压力下降到当前的地层压力,气藏压降为∆p,水体中的水会因气藏压力下降而侵入气藏,气藏含气半径减小,设减小量为∆r,以水侵圆环为研究对象,研究水侵前后圆环部分储层各种体积参数的变化(图 1)。
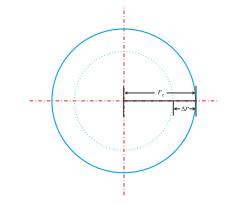 |
| 图1 气藏水侵示意图 Fig. 1 The schematic diagram of gas reservoir water invasion |
水侵圆环原始条件下的孔隙体积、束缚水和含气体积分别为
| $ {V_{\rm{p}}} = \pi \left[{r_{\rm{e}}^2-{{\left( {{r_{\rm{e}}}-\Delta r} \right)}^2}} \right]h\phi $ | (1) |
| $ {V_{{\rm{wc}}}} = \pi \left[{r_{\rm{e}}^2-{{\left( {{r_{\rm{e}}}-\Delta r} \right)}^2}} \right]h\phi {S_{{\rm{wc}}}} $ | (2) |
| $ {V_{{\rm{gi}}}} = \pi \left[{r_{\rm{e}}^2-{{\left( {{r_{\rm{e}}}-\Delta r} \right)}^2}} \right]h\phi \left( {1 -{S_{{\rm{wc}}}}} \right) $ | (3) |
当气藏压力下降时,水侵圆环的孔隙受压缩体积会减小,水侵圆环的束缚水会膨胀,孔隙减小体积和水侵圆环的束缚水膨胀体积分别为
| $ \Delta {V_{\rm{p}}} = {V_{\rm{p}}}{C_{\rm{p}}}\Delta p = \pi \left[{r_{\rm{e}}^2-{{\left( {{r_{\rm{e}}}-\Delta r} \right)}^2}} \right]h\phi {C_{\rm{p}}}\Delta p $ | (4) |
| $ \Delta {V_{{\rm{wc}}}} = {V_{{\rm{wc}}}}{C_{\rm{w}}}\Delta p = \pi \left[{r_{\rm{e}}^2-{{\left( {{r_{\rm{e}}}-\Delta r} \right)}^2}} \right]h\phi {S_{{\rm{wc}}}}{C_{\rm{p}}}\Delta p $ | (5) |
令Γ=(1 − Swc) − (Cp + SwcCw) ∆p,水侵圆环中原本含气而被侵入地层水占据的孔隙体积可表示为
| $ {V_{\rm{c}}} = {V_{{\rm{gi}}}}- \Delta {V_{\rm{p}}}- \Delta {V_{{\rm{wc}}}} = \pi \left[{r_{\rm{e}}^2-{{\left( {{r_{\rm{e}}}-\Delta r} \right)}^2}} \right]h\phi \mathit{\Gamma} $ | (6) |
在水体刚刚推进至井底时,气井尚不产水,圆环中原本含气而被侵入地层水占据的孔隙体积即为水侵量We。在水体推进到井底以后,气井开始产地层水,有效水侵量为We − WpBw,有
| $ {V_{\rm{c}}} = {W_{\rm{e}}}-{W_{\rm{p}}}{B_{\rm{w}}} $ | (7) |
将式(7)代入式(6),整理,得
| $ \Delta r = {r_{\rm{e}}}-\sqrt {r_{\rm{e}}^2-\frac{{{W_{\rm{e}}}-{W_{\rm{p}}}{B_{\rm{w}}}}}{{\pi h\phi \mathit{\Gamma} }}} $ | (8) |
如果气藏不是圆形的,具有一定的水侵角,引入水侵角分数f修正方程
| $ \Delta r = {r_{\rm{e}}} - \sqrt {r_{\rm{e}}^2 - \frac{{{W_{\rm{e}}} - {W_{\rm{p}}}{B_{\rm{w}}}}}{{f\pi h\phi \mathit{\Gamma} }}} $ | (9) |
根据式(9)可计算得到水体推进距离,在计算得到水体推进距离之后,根据地层倾角α可计算得到水体上升高度
| $ \Delta h = \Delta r\sin \alpha $ | (10) |
在已知气藏压力和水侵量时,采用式(9)可以计算水体平面推进距离,采用式(10)可以计算水体上升高度,结合气井射孔层段就可明确开发过程中受边水影响的气井,及早进行开发调整,实现水侵预警的目的。
2 动态预测辅助模型的建立在采用式(9)和式(10)预测气藏水侵动态时,需要已知气藏水侵量和气藏压力,而气藏水侵量和气藏压力又是随产量变化的参数。因此,要全面预测气藏动态,还需要产量预测模型、水侵量计算模型和压力计算模型的辅助。
2.1 产量预测模型在已知气藏压力时,将平均单井产气量qg代入产能方程可求得井底流压pwf。在求得井底流压后,根据各井轨迹、气藏流体性质,采用垂直管流模型计算各井在平均单井产气量时的气井井口压力pwh。设井口外输压力为pwo,则当pwh≥pwo时,气藏产能在规划产量Q下能够稳产;当pwh < pwo时,气藏产能在规划产量Q下不能稳产。采用非线性搜索的方式,重复上述计算步骤,计算pwh=pwo时的产量,该产量即为该预测时间节点的最大年产气量Qmax。
气藏产量预测模型如下
| $ \left\{ {\begin{array}{*{20}{l}} {{q_{\rm{g}}} = \frac{Q}{{365n}}}\\ {p_{\rm{R}}^2-p_{{\rm{wf}}}^2 = A{q_{\rm{g}}} + Bq_{\rm{g}}^2}\\ {\frac{{{\rm{d}}p}}{{{\rm{d}}z}} = \rho {\rm{g}}\sin \theta + \frac{{\rho {v^2}{f_{\rm{r}}}}}{{2D}} + \rho v\frac{{{\rm{d}}v}}{{{\rm{d}}z}}}\\ {{G_{\rm{p}}} = \sum\limits_{t = 1}^m {{Q_t}} } \end{array}} \right. $ | (11) |
稳定期和递减期限定条件分别为pwh≥pwo和pwh=pwo。
2.2 压力预测模型在根据建立的产量预测模型预测气藏产量时,需要已知气藏前一个时间节点的气藏压力,气藏压力可根据水驱气藏物质平衡方程计算[14-16]。
用压力表示的水驱气藏物质平衡方程为
| $ \frac{{{p_{\rm{i}}}}}{{{Z_{\rm{i}}}}}\left( {1- \frac{{{G_p}}}{G}} \right) = \frac{p}{Z}\left[{1-\frac{{{W_{\rm{e}}}-{W_{\rm{p}}}{B_{\rm{w}}}}}{{G{B_{{\rm{gi}}}}}}} \right] -\frac{p}{Z}\left( {\frac{{{C_{\rm{p}}} + {S_{{\rm{wc}}}}{C_{\rm{w}}}}}{{1 -{S_{{\rm{wc}}}}}}} \right)\Delta p $ | (12) |
由于水驱气藏地层压力可表示为
| $ {p_{\rm{H}}} = \frac{p}{Z}\left[{1-\left( {\frac{{{C_{\rm{p}}} + {S_{{\rm{wc}}}}{C_{\rm{w}}}}}{{1-{S_{{\rm{wc}}}}}}} \right)\Delta p-\frac{{{W_{\rm{e}}} - {W_{\rm{p}}}{B_{\rm{w}}}}}{{G{B_{{\rm{gi}}}}}}} \right] $ | (13) |
水驱气藏物质平衡方程可变为
| $ {p_{\rm{H}}} = \frac{{{p_{\rm{i}}}}}{{{Z_{\rm{i}}}}}\left( {1-\frac{{{G_{\rm{p}}}}}{G}} \right) $ | (14) |
从式(14)来看,水驱气藏压力pH与气藏累产气量Gp呈线性关系,在已知气藏水侵量时,可根据气藏累产气量计算气藏压力。
2.3 水侵量计算模型根据式(9)和式(10)计算水体推进距离和根据式(12)~式(14)计算气藏压力时均需要已知水侵量。目前,计算水驱气藏水侵量的计算模型很多[17-20],有罐状水层模型、Schilthuis稳态模型、Fetkovitch方法、Hurst修正稳态模型、Van Everdingen-Hurst非稳态模型、Carter-Tracy非稳态模型等多种方法。水侵量计算模型应根据气藏实际情况选择适合该气藏的水侵量计算模型[21-24]。
3 气藏水侵动态预测实例计算以PG气田为例开展气藏水侵动态预测实例计算。利用气田主体气藏气井在投产时的单点测试结果,求得平均二项式产能方程为
| $ p_{\rm{R}}^2-p_{{\rm{wf}}}^2 = 1.8292{q_{\rm{g}}} + 0.0150q_{\rm{g}}^2 $ | (15) |
根据气田水体能量大小研究的结果,Fetkovitch方法适合用于计算气田主体气藏水侵量。
3.1 预测流程联立前述建立的水侵预警方程、产量预测模型、压力预测模型和水侵量计算模型形成完整的水驱气藏水侵动态预测数学模型,依此数学模型可对气藏的开发指标和水侵动态进行预测,预知气藏未来的开发动态,预测流程如图 2。
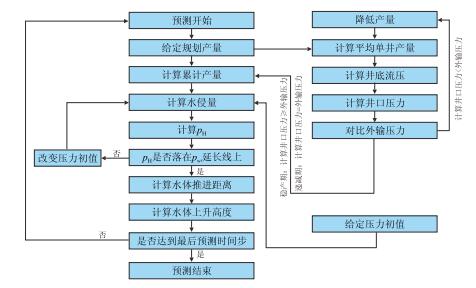 |
| 图2 水驱气藏开发指标及水侵动态预测流程图 Fig. 2 The prediction flowchart of production index and water invasion performance of water-drive gas reservoir |
以PG气田主体气藏2011年底生产资料为基础,根据建立的水驱气藏开发动态预测模型预测未来15 a的开发动态,预测结果见表 1~表 2。
| 表1 PG气田主体气藏开发动态预测结果表 Table 1 The prediction result on development performance of PG gas reservoir |
| 表2 PG气田主体气藏预测稳产期内可能见水井统计表 Table 2 The statistic on possible water production wells of PG gas reservoir |
按年产80.00×108 m3规划产量,气藏可稳产至2018年,加上历史产量,折合稳产年限为8.68 a。稳产期末累产气694.16×108 m3,采出程度为38.33%。稳产期末气藏压力29.79 MPa,稳产期末水侵量0.309×108 m3,水体上升高度98.83 m。稳产期内可能见水的井有P101-2H,P103-1,P103-2,P103-4,P104-1,P104-3,P105-1H,P105-2,P106-2H,P203-1,P304-1和P305-2。
4 结论(1) 在物质平衡理论基础上建立的圆形边水气藏水侵预警方程,能预测气藏的可能见水井及其见水时间,可实现水侵气藏的早预警、早调整。
(2) 将水侵预警方程辅以产量预测模型、压力预测模型和水侵量计算模型,建立了一种新的边水气藏生产动态预测方法。应用于PG气田水侵气藏的见水井、见水时间和相关开发指标的动态预测与实际生产对比表明,该模型预测结果基本吻合,能够指导气藏的水侵预警与及时调整。
符号说明
∆p—压降,MPa;∆r—含气半径减小量,m;re—气藏半径,m;Vp—孔隙体积,m3;Vwc—束缚水体积,m3;Vgi—含气体积,m3;h—气层厚度,m;ϕ—孔隙度,无因次;Swc—束缚水饱和度,无因次;Cp—岩石压缩系数,MPa−1;Cw—地层水压缩系数,MPa−1;We—水侵量,×108 m3;Wp —累产水量,×108 m3;Bw—地层水体积系数,无因次;f —水侵角分数,无因次;α—地层倾角,(°);∆h—水体上升高度,m;qg—单井产气量,×104 m3/d;pwf —井底流压,MPa;pwh—井口压力,MPa;pwo—井口外输压力,MPa;Q—气藏规划产量,×108 m3/a;n—气藏总井数;pR—井区平均地层压力,MPa;p—压力,MPa;z—深度,m;ρ—流体密度,kg/cm3;g—重力加速度,g=9.81 m/s2;θ—井斜角,(°);fr—摩阻系数,无因次;D—管柱内径,m;v—流速,m/s;Gp—累积产气量,×108 m3;Qt—第t年产气量,×108 m3/a;pi—原始地层压力,MPa;Zi—原始条件下的天然气偏差因子,无因次;Z—目前条件下的天然气偏差因子,无因次;G—气藏储量,×108 m3;pH—水驱气藏地层压力,MPa;Bgi—原始气体体积系数,无因次。
| [1] | Roopa I V, Baksh K. Predicting water breakthrough using pressure transient analysis in a gas condensate reservoir in the Columbus Basin, Trinidad[C]. SPE 158496, 2012. |
| [2] | Amarfio E M, Igbokoyi A O. Breakthrough time correlations for coning in bottom water supported reservoirs[C]. SPE 167511, 2013. |
| [3] |
谢学恒, 秦学成. 煤层气井见气时间预测方法及其应用[J].
煤矿开采, 2013, 18 (4) : 5 –7.
Xie Xueheng, Qin Xuecheng. Method of predicting methane emerging time in coal-bed methane shaft and its application[J]. Coal Mining Technology, 2013, 18 (4) : 5 –7. |
| [4] |
吴克柳, 李相方, 张公涛, 等. 考虑反凝析的边水凝析气藏见水时间预测新方法[J].
科学技术与工程, 2011, 11 (19) : 4574 –4577.
Wu Keliu, Li Xiangfang, Zhang Gongtao, et al. A novel approach to predict water breakthrough time in gas condensate reservoir with edge water considering retrograde condensation[J]. Science Technology and Engineering, 2011, 11 (19) : 4574 –4577. |
| [5] |
张庆辉, 李相方, 张磊, 等. 考虑启动压力梯度的低渗底水气藏见水时间预测[J].
石油钻探技术, 2012, 40 (5) : 96 –99.
Zhang Qinghui, Li Xiangfang, Zhang Lei, et al. Prediction of water breakthrough time in low permeability gas reservoirs with bottom water in consideration of threshold pressure[J]. Petroleum Drilling Techniques, 2012, 40 (5) : 96 –99. |
| [6] |
王会强, 李晓平, 吴锋, 等. 边水气藏气井见水时间预测方法[J].
特种油气藏, 2008, 15 (4) : 73 –74, 93.
Wang Huiqiang, Li Xiaoping, Wu Feng, et al. Prediction of water breakthrough time in gas reservoirs with edge water[J]. Special Oil & Gas Reservoirs, 2008, 15 (4) : 73 –74, 93. |
| [7] | Sun H. A new method for low permeability gas well performance prediction using pressure transient analysis:Theory and practices[C]. SPE 144952, 2011. |
| [8] |
熊健, 胡永强, 陈朕, 等. 考虑真实气体的低渗气藏动态预测模型[J].
东北石油大学学报, 2013, 37 (2) : 91 –95.
Xiong Jian, Hu Yongqiang, Chen Zhen, et al. Dynamic prediction model for the low-permeability gas reservior taking the real gas into account[J]. Journal of Northeast Petroleum University, 2013, 37 (2) : 91 –95. |
| [9] |
孙贺东. 具有补给的气藏物质平衡方程及动态预测[J].
石油学报, 2011, 32 (4) : 683 –686.
Sun Hedong. A balance equation of gas materials with recharge capacity and their performance prediction[J]. Acta Petrolei Sinica, 2011, 32 (4) : 683 –686. |
| [10] |
孙贺东, 毛小平, 康博. 矩形气藏的产量递减规律及动态预测方法[J].
天然气工业, 2011, 31 (7) : 40 –42.
Sun Hedong, Mao Xiaoping, Kang Bo. Production prediction and decline laws of rectangular gas reservoirs[J]. Natural Gas Industry, 2011, 31 (7) : 40 –42. |
| [11] | 阳仿勇, 张烈辉, 陈军.异常高压气藏动态预测模型及应用[J].西南石油学院学报, 2004, 26(6):24-27. overpressure gas reservoir[J]. Journal of Southwest Petroleum Institute, 2004, 26(6):24-27. |
| [12] |
吴克柳, 李相方, 范杰, 等. 异常高压凝析气藏水侵量及水体大小计算方法[J].
中国矿业大学学报, 2013, 42 (1) : 105 –111.
Wu Keliu, Li Xiangfang, Fan Jie, et al. An approach to calculate water influx and aquifer regien of abnormally high pressure condensate gas reservoir[J]. Journal of China University of Mining & Technology, 2013, 42 (1) : 105 –111. |
| [13] |
孙恩慧, 李晓平. 物质平衡方程在含硫异常高压有水气藏的应用[J].
天然气勘探与开发, 2013, 36 (1) : 40 –42.
Sun Enhui, Li Xiaoping. Application of matter-balance equation to sour-gas reservoir with abnormal pressure and water[J]. Natural Gas Exploration & Development, 2013, 36 (1) : 40 –42. |
| [14] | Moghadam S, Jeje O, Mattar L. Advanced gas material balance in simplified format[J]. Journal of Canadian Petroleum Technology, 2011, 50 (1) : 90 –98. DOI:10.2118/139428-PA |
| [15] | 陈恒, 杜建芬, 谢远新, 等. 凝析气藏物质平衡方程研究现状及进展[J]. 新疆石油科技, 2013, 23 (1) : 24 –26. |
| [16] |
郭平, 欧志鹏. 考虑水溶气的凝析气藏物质平衡方程[J].
天然气工业, 2013, 33 (1) : 70 –74.
Guo Ping, Ou Zhipeng. Material balance equation of a condensate gas reservoir considering water soluble gas[J]. Natural Gas Industry, 2013, 33 (1) : 70 –74. |
| [17] |
熊伟, 朱志强, 高树生, 等. 考虑封闭气的水驱气藏物质平衡方程[J].
石油钻探技术, 2012, 40 (2) : 93 –97.
Xiong Wei, Zhu Zhiqiang, Gao Shusheng, et al. Material balance equation of waterflooding gas reservoir considering trapped gas[J]. Petroleum Drilling Techniques, 2012, 40 (2) : 93 –97. |
| [18] |
刘道杰, 刘志斌, 田中敬. 改进的异常高压有水气藏物质平衡方程[J].
石油学报, 2011, 32 (3) : 474 –478.
Liu Daojie, Liu Zhibin, Tian Zhongjing. A modified material balance equation for abnormal pressure gas reservoirs with aquifer[J]. Acta Petrolei Sinica, 2011, 32 (3) : 474 –478. |
| [19] |
刘志斌, 刘道杰, 田中敬. 高温高压凝析气藏物质平衡方程的建立——考虑气藏气相水蒸气含量及岩石颗粒的弹性膨胀作用[J].
天然气工业, 2011, 31 (7) : 37 –39.
Liu Zhibin, Liu Daojie, Tian Zhongjing. Establishment of material balance equation of HPHT gas condensate reservoirs:Taking into account the water vapor content of gas phase and the elastic expansion of rock particles[J]. Natural Gas Industry, 2011, 31 (7) : 37 –39. |
| [20] |
姚翔, 董杰, 杨慧, 等. 基于物质平衡和水侵量的边水容量计算[J].
油气地球物理, 2013, 11 (2) : 60 –62, 67.
Yao Xiang, Dong Jie, Yang Hui, et al. Edge water capacity calculation based on material balance and the water influx[J]. Petroleum Geophysics, 2013, 11 (2) : 60 –62, 67. |
| [21] |
王星, 黄全华, 尹琅, 等. 考虑水侵和补给的气藏物质平衡方程的建立及应用[J].
天然气工业, 2010, 30 (9) : 32 –35.
Wang Xing, Huang Quanhua, Yin Lang, et al. Setting-up and application of thematerial balance equations for a gas reservoir considering water influx and supply region[J]. Natural Gas Industry, 2010, 30 (9) : 32 –35. |
| [22] |
胡俊坤, 李晓平, 敬伟, 等. 确定水驱气藏动态储量及水侵量的新方法[J].
新疆石油地质, 2012, 33 (6) : 720 –722.
Hu Junkun, Li Xiaoping, Jing Wei, et al. A new method for determining dynamic reserves and water influx in water drive gas reservoir[J]. Xinjiang Petroleum Geology, 2012, 33 (6) : 720 –722. |
| [23] |
邓成刚, 孙勇, 曹继华, 等. 柴达木盆地涩北气田地质储量和水侵量计算[J].
岩性油气藏, 2012, 24 (2) : 98 –101.
Deng Chenggang, Sun Yong, Cao Jihua, et al. Calculation of original gas in place and water influx in the Sebei Gas Field, Qaidam Basin[J]. Lithologic Reservoirs, 2012, 24 (2) : 98 –101. |
| [24] |
刘道杰, 刘志斌, 田中敬, 等. 异常高压有水气藏水侵规律新认识[J].
石油天然气学报, 2011, 33 (4) : 129 –132.
Liu Daojie, Liu Zhibin, Tian Zhongjing, et al. New understanding of water invasion rules of aquifer gas reservoirs with over-pressure[J]. Journal of Oil and Gas Technology, 2011, 33 (4) : 129 –132. |
 2014, Vol. 36
2014, Vol. 36

