2. 中国石油大庆油田有限责任公司勘探事业部, 黑龙江 大庆 163453
2. Exploration Division, Daqing Oilfield Company Ltd, PetroChina, Daqing, Heilongjiang 163453, China
随着勘探目标的日趋复杂,勘探难度不断加大,近年来,松辽盆地北部中浅层扶余油层成为了大庆油田的勘探的主战场之一。扶余油层由于特殊的沉积地质原因,地层砂地比相对较低,油藏类型以断层—岩性油藏、构造—岩性油藏或者岩性油藏为主,而这些类型油藏的成藏主控因素是河道砂体储层,河道砂体预测是勘探的关键。然而,该油层河道砂体主要特点是厚度薄,一般为2~5 m,其次为1~2 m,但是地震主频在50 Hz左右,速度在3 500 m/s左右,河道砂体的厚度远远小于地震1/4波长;加之横向变化快的特点,河道砂体的准确识别、砂体厚度的精确描述就成为了该油层的勘探开发最主要的难题之一。
针对上述难题,开展了大量的攻关研究,地震资料的保幅高分辨率处理和解释技术得到了不断进步,地震资料的相对保真性不断提高,地震解释技术丰富完善,地震属性对于地质体的横向分辨能力得到了大大加强,目前利用地震属性定性预测河道砂体在实际应用中取得了良好的效果[1],能够预测出砂体相对较厚的河道发育带。在此基础之上,研究人员为了满足油藏精细评价的需求,采用了多种方法开展河道砂体储层厚度定量预测研究,比如叠后井约束反演等狭义反演,但其结果的井间插值现象往往较为严重,在很大程度上对地震资料的横向分辨能力有所降低,所以最终不能成为解决问题的有效方法。为此,作者探索了基于各种地震属性,采用线性回归法、神经网络法、支持向量机[2-10]等方法拟合多种地震属性与砂体厚度之间的关系。经研究发现,与线性回归法和神经网络法相比,支持向量机具有如下优势:(1)它是建立在结构风险最小化原则以及VC维概念基础上的一种专门针对小样本的统计学习理论;(2)它对于非线性回归问题具有更加优越的泛化性能;(3)算法中将求解问题转化为一个二次型寻优问题,从理论上来说,必将得到全局最优解,避免了神经网络中可能陷入局部最优的困境。针对实际地质问题,为了获取更好的预测效果,提出首先用相对保幅地震数据提取能够高精度定性预测地震相和河道砂体相对厚度的有效地震属性,然后在专家优化地震属性组合的基础上确定支持向量机模型,最后用该模型定量储层厚度,从而达到既能保持三维地震高横向分辨能力又能精确预测河道砂体厚度的目的。该方法在松辽盆地北部ZYN地区的扶余油层河道砂体厚度定量预测实际应用中取得良好效果。
1 支持向量机原理及模型支持向量机(Support Vector Machine,SVM)是20世纪90年代中期发展起来的,它是建立在结构风险最小化原则以及VC维概念基础上的一种有限样本统计学习理论[9-12]。其核心思想是通过核函数将非线性问题映射到一个高维特征空间,在高维空间中基于结构风险最小化原理构造线性回归函数。
SVM模型的建立主要包括两方面工作:一是选择核函数,二是确定SVM相关参数,主要指核函数参数以及正则化参数C的选择。设样本集为:
| $ \begin{equation} \mathop {\max }\limits_{\alpha ,{\alpha _{i}}} W(\alpha ,{\alpha ^{\rm{*}}}) = \mathop {\max }\limits_{\alpha ,{\alpha _{i}}} \left\{ \begin{array}{*{20}{c}} {\sum\limits_{{i} = 1}^{l} {\alpha _i^*({y_i} - \epsilon ) - {\alpha _i}({y_i} + \epsilon )} }\\ { - \frac{1}{2}\sum\limits_{i = 1}^l {\sum\limits_{j = 1}^l {(\alpha _i^* - {\alpha _i})(\alpha _j^* - {\alpha _j})K({x_i},{x_j})} } } \end{array}\right\} \end{equation} $ | (1) |
其约束条件为
| $ 0 \leqslant {\alpha _{i}} \leqslant C, {{i}} = 1, ..., l;\\ {0 \leqslant \alpha _i^{*} \leqslant C, i = 1, ..., l};\\ \sum\limits_{i = 1}^I {(\alpha _i^{*} - {\alpha _i}) = 0。} $ |
由此可得拉格朗日待定系数
| $ {{f}}(x) = \sum\limits_{S{V_{\rm{s}}}} {(\overline {{\alpha _i}} - {{\overline {{\alpha _i^*}} }})K({x_i}, x)} $ | (2) |
式中:C—损失函数,无因次,代表对误差的宽容度,值越大代表对误差容忍程度越小,训练速度越慢,泛化能力也相对越差;ϵ—不敏感损失函数参数,无因次,取值[0, 1],代表泛化能力;
通过已知样本即地震属性组合和储层参数学习训练式(3),得到预测函数f(x),进而可根据优化后的地震属性组合预测储层参数。
根据支持向量机模型进行储层参数预测,具体步骤可描述为
(1)专家优化地震属性组合及归一化;
(2)建立学习样本集
(3)SVM的模型参数选择;
(4)通过已知样本(即优化后的地震属性组合)和储层参数训练,建立回归预测函数;
(5)输入优化后的地震属性组合对储层参数进行预测。
2 地震属性优选与SVM模型参数选择 2.1 地震属性优选地震属性种类繁多,且各类属性的地质含义也有所不同[13-17],在实际的应用中,需要针对地质目标优选出有效的地震属性开展预测工作。输入的地震属性应该尽可能针对地质目标体的特性考虑全面,在地球物理理论基础之上,开展研究区地质规律调查,综合分析与优选组合,主要依据如下:
(1)原理上,所选类型地震属性可以定性或者半定量地预测所研究目标;
(2)实际中,在对研究区宏观地质规律把握的基础之上,详细总结河道砂体的特点,选择与沉积相认识相吻合的多种地震属性;
(3)研究区的地震资料与钻井资料的联合标定结果能够说明,优选的地震属性能在井点处反映预期的储层物性参数,这同时也是在检验地震资料是否达到了保幅处理要求。
然而单一的地震属性用于薄层地质体的厚度定量预测的风险往往较大,需要优化组合多种有效属性来解决。
2.2 SVM模型参数选择 2.2.1 核函数的选择目前研究较多的核函数主要有多项式核函数、Gauss径向基核函数、Sigmoid核函数及RBF核函数。在支持向量机模型研究中,RBF核函数是目前被广泛应用的一种核函数。
2.2.2 SVM相关参数的选择主要包括损失函数C、不敏感损失函数参数ε以及γ系数。以上参数的选择直接影响着支持向量机的泛化性能和回归估计的精度,并且泛化性能和回归估计的精度相互制约。例如,每个数据子空间至少存在一个合适的C值,使得SVM泛化性能最好。正则化参数C能够使模型的复杂度和训练误差之间取一个折中,以便使模型有较好的推广能力,不同数据的子空间中最优的C值不同。在确定的数据子空间中,参数C取得太小,则对样本数据中超出ε不敏感带的样本惩罚就越小,使训练误差变大,系统的泛化能力变差,会出现“欠学习”现象;C取得太大,相应的权重就小,系统的泛化能力变差,会出现“过学习”现象。
结合研究区地质需求,本文采用以下方法衡量支持向量机的泛化性能和回归精度:支持向量机的泛化性能以河道砂体厚度预测结果是否与优选出的地震属性图的整体变化趋势相吻合来衡量。回归精度用训练误差和验证误差来衡量。训练误差是指应用全区已知井全部参与训练,用预测结果与随机抽取的部分已知井测井解释的储层参数数据计算训练误差,要求平均相对误差小于15%。验证误差是指在研究区的已知井中抽取部分井作为后验井,用预测结果与后验井的测井解释数据计算验证误差,要求平均相对误差小于30%。
3 应用实例 3.1 工区概况ZYN地区位于松辽盆地北部中央拗陷区和东南隆起区两个一级构造单元交接部位,同时跨越朝阳沟阶地和长春岭背斜带两个二级构造单元。其构造背景总体上表现为向西北倾单斜。该地区扶余油层砂地比低,区内扶杨油层受构造、岩性双重控制易形成构造—岩性油藏、岩性油气藏。区内三维地震面积200 km2,收集到探井、评价井资料34口。
从该区探井综合柱状图(图 1)可以看出,河道砂体是本区主要的储集砂体,在测井相上表现为底部突变、顶部渐变的倒漏斗型或者钟型,加之在岩芯上体现为二元沉积结构,所以该区为典型的陆相曲流河沉积环境,具有砂体横向变化剧烈的特征,边界难以准确识别。单砂体很薄,一般都小于5 m,地震资料纵向分辨率低(50 Hz左右),河道砂体厚度的定量预测难度较大。
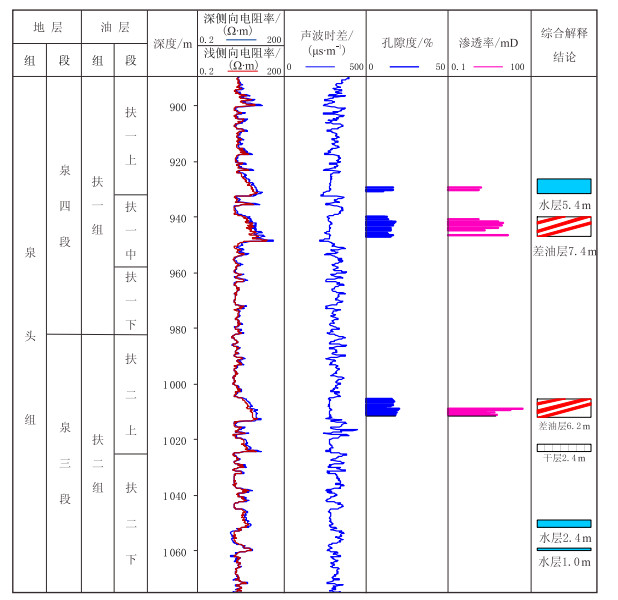 |
| 图1 ZYN地区C47井扶余油层综合柱状图 Fig. 1 The histogram of Fuyu layer of C47 in ZYN Area |
该区扶余油层的河道砂体具有相对高密度、高速度的特点,泥岩相反具有相对低密度、低速度的特点。地层中砂泥岩的组合关系基本上为泥包砂的组合模式,在较厚砂岩顶部呈正极性的中强振幅反射特征;正演研究表明,对于这类小于1/4波长情况,地震振幅响应是随着砂岩厚度增大而变强的[11];以上是本文选择最大峰值振幅属性作为关键参数输入模型的主要理论根据。瞬时相位属性和瞬时频率属性原理上都能反映地层中岩性的变化,本文分别进行了提取。河道砂体的空间变化剧烈,本文选择地震相干属性来预测河道砂体边界,以利于模型计算在厚度突变处的收敛。为了更好地使预测结果符合沉积地质规律,本文重点开展了地震相分析,将波形分类属性作为模型输入的主要参数。
以该地区扶一中油层组(Fz 1)为例,地震属性与已知井的地质资料进行了对比,最大峰值振幅属性反映3 m以上砂岩的符合率在80%以上,图 2中的强值区(图中暖色调黄、红)砂岩较相对厚,弱值区(图中冷色调浅蓝、蓝)为砂岩相对较薄。瞬时相位属性和瞬时频率属性反映河道砂体分布也具有较好的效果。地震道波形分类属性(图 3)地震相分析结果与平均反射强度属性图在反映沉积地质规律方面具有很好的一致性,合理地反映了曲流河点坝(红框处)等地震沉积相特征,曲流河的弯度中等,河道的侧向迁移比较明显,侧积形成的点砂坝砂体为该中沉积环境中的主要优质储集砂体。地震相干属性(图 4)的物理意义在于检测地质目标体的横向不连续性,河道砂体内部为相对干净的均匀特点(红框处),河道砂体边界和废弃河道特征得到清晰刻画(红色箭头处)。
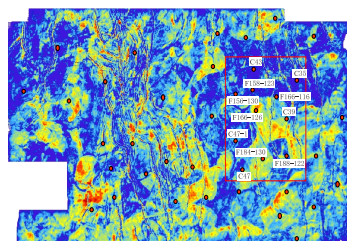 |
| 图2 ZYN地区扶一中油层组最大峰值振幅属性图 Fig. 2 The maximum peak amplitude attribute map of Fz 1 layer in ZYN Area |
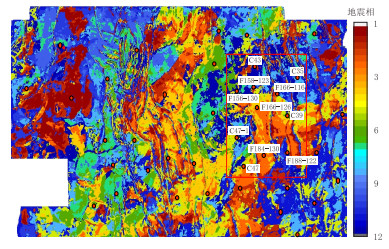 |
| 图3 ZYN地区扶一中油层组波形分类地震相属性图 Fig. 3 The waveform classification seismic face attribute map of Fz 1 layer in ZYN Area |
 |
| 图4 ZYN地区扶一中油层组地震相干属性图 Fig. 4 The seismic coherence attribute map of Fl z layer in ZYN Area |
图 5为本文的研究思路流程图,5种属性作为输入参数,但是量纲不一、数值量级有差异,所以首先将它们进行归一化处理;然后以3个参数为一组的方式分多种不同组合在支持向量机模型中与工区中随机的28口已知井的河道砂体厚度开展拟合,用剩下的6口井作为后验井。本文模型采用RBF核函数,计算结果表明,由于本区的地震资料主频对于薄砂体的分辨能力低,同时,单斜背景构造起伏大、断层十分发育的影响,瞬时频率属性参与的几个组合的回归精度较低,频率属性图虽然能够反映砂体的平面分布规律,但是其数值大小与河道砂体厚度并没有良好的相关性;瞬时相位属性对于在地震剖面上的采样点十分敏感,而对于河流相复杂沉积地层结构,地震层位解释在相位上的精度很难保证,瞬时相位属性在模型试算后也未被采纳。因而,本文选择了最大峰值振幅属性、波形分类属性和地震相干属性组合,以便预测结果满足支持向量机模型的泛化性能和回归精度。不同参数组合预测结果的对比分析表明,损失函数C对厚度值的分布范围影响较大,ε取值大小直接影响回归估计的精度,总体上看,γ取值越大砂体厚度分布的连续性越好,最终确定出损失函数C取值30、不敏感损失函数参数ε取值0.01、以及γ系数取值128。最终,全工区的34口井及优选的属性组合参与计算,预测结果如图 6所示。
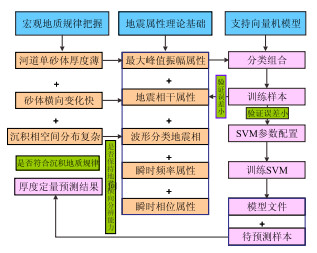 |
| 图5 支持向量机厚度预测研究流程图 Fig. 5 The flow chart of SVM thickness calculation |
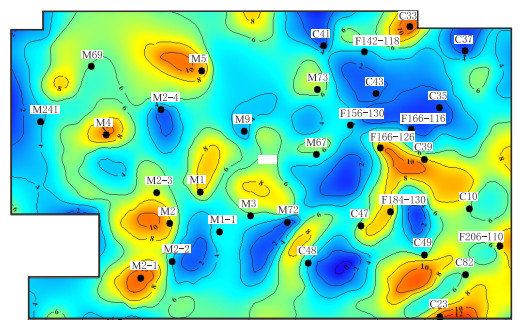 |
| 图6 ZYN地区扶一中油层组砂岩厚度图 Fig. 6 The sandstone thickness map of Fz 1 layer in ZYN Area |
该区扶一中油层组的砂体分布形态以条带状为主,局部砂岩较厚为点砂坝沉积结果,符合曲流河沉积环境的认识。砂岩定量预测结果与最大峰值振幅属性(图 2)和波形分类地震相属性(图 3)所揭示的砂体分布规律基本一致,表明地震相在模型计算中起到了很好的横向控制作用。研究区主体为自西南向东北推进的曲流河及其上分布的决口河道,区内东南部曲流河河道发育,自南向北东方向流入;另外,工区的西南部曲流河道也较发育,向北东方向延伸,河道砂体厚度也较大。区内东北部主体部位决口扇沉积砂体发育,砂岩厚度相对较薄。砂体厚度横向变化快,比如其中一处点砂坝的(红框处,C-47,F166-126)的砂体厚度较厚,点砂坝的以外区域砂岩快速变薄,如C43、C35等区域为泛滥平原相的区域,砂岩非常薄。该图应用于勘探部署中,预测M73井位置河道砂岩较发育、该油层组层砂岩总厚度7.6 m,经钻井验证,M73井在扶一中油层组钻遇单砂体厚度3.8 m的河道砂体,砂岩总厚度6.0 m,预测误差为0.27。
4 结语(1)河道砂体厚度定量预测时,首先应该充分认识河流相沉积地质规律和砂体特征,然后有针对性地求取有效地震属性。地震资料的保幅处理是基础,单一地震属性对于河道砂体的空间剧变特性很难精确控制,但不是属性种类越多越好,应该在拟合过程中优化组合,应用最有效的参数组合。
(2)采用支持向量机模型预测河道砂体厚度,能够较好地保持地震属性的横向分辨能力,预测结果与已知井的符合程度高,且砂体分布符合沉积地质规律;同时又受地震属性值与砂体厚度值相关性的制约。
| [1] |
张尔华, 陈树民, 宋永忠, 等. 突出河道砂体地质特征的地震保幅处理技术——以松辽盆地北部扶余油层为例[J].
地质科学, 2009, 44 (2) : 722 –739.
Zhang Erhua, Chen Shumin, Song Yongzhong, et al. Preserved amplitude processing aimed at enhancing geological characteristics of channel sandbodies:A case study from Fuyu oil layer in the northern Songliao Basin[J]. Chinese Journal of Geology, 2009, 44 (2) : 722 –739. |
| [2] |
陈树民, 沈加刚, 宋永忠, 等. 基于沉积模式的地震多属性量化沉积微相解释方法——以松辽盆地北部高台子地区泉头组三, 四段为例[J].
地质科学, 2009, 44 (2) : 740 –758.
Chen Shumin, Shen Jiagang, Song Yongzhong, et al. Method of interpretation by quantization of multiple seismic attributes based on sedimentary model:A case study from Members 3-4, Quantou Formation in the northern Songliao Basin[J]. Chinese Journal of Geology, 2009, 44 (2) : 740 –758. |
| [3] |
吴胜和, 杨延强. 地下储层表征的不确定性及科学思维方法[J].
地球科学与环境学报, 2012, 34 (2) : 72 –80.
Wu Shenghe, Yang Yanqiang. Uncertainty and scientific methodology in subsurface reservoir characterization[J]. Journal of Earth Sciences and Environment, 2012, 34 (2) : 72 –80. |
| [4] | Li J K, Castagna J, Li D G, et al. Reservoir Prediction Via SVM Pattern Recognition[C]. SEG Annual Meeting, 2004, 425-429. |
| [5] | Zhao B, Brouwer F, Aminzadeh F, et al. Multiple prediction and reservoir characterization of a tight sand reservoir[C]. SEG Annual Meeting, 2008. |
| [6] | Zhang C K, Lu W K. Seismic attributes selection based on SVM for hydrocarbon reservoir prediction[C]. SEG Annual Meeting, 2010. |
| [7] |
张大智, 纪友亮, 刘洪林, 等. 基于BP神经网络的薄互层储层预测[J].
上海地质, 2005 (4) : 47 –50.
Zhang Dazhi, Ji Youliang, Liu Honglin, et al. Thin-inter bed reservoir prediction based on BP neural network[J]. Shanghai Geology, 2005 (4) : 47 –50. |
| [8] |
张彦周, 刘叶玲, 谢宝英. 支持向量机在储层厚度预测中的应用[J].
勘探地球物理进展, 2005, 28 (6) : 422 –424.
Zhang Yanzhou, Liu Yeling, Xie Baoying. Application of SVM in prediction of reservoir thickness[J]. Progress in Exploration Geophysics, 2005, 28 (6) : 422 –424. |
| [9] | Learning V C V. Guest editorial Vapnik-chervonenkis (VC) learning theory and its applications[J]. IEEE Transactions on Neural Netwoks, 1999, 10 (5) : 985 –987. DOI:10.1109/TNN.1999.788639 |
| [10] |
张尔华, 关晓巍, 张元高. 支持向量机模型在火山岩储层预测中的应用——以徐家围子断陷徐东斜坡带为例[J].
地球物理学报, 2011, 54 (2) : 428 –432.
Zhang Erhua, Guan Xiaowei, Zhang Yuangao. Support vector machine in volcanic reservoir forecast:East slope in Xujiaweizi Depression[J]. Chinese Journal of Geophysics, 2011, 54 (2) : 428 –432. |
| [11] |
凌云研究组. 地震分辨率极限问题的研究[J].
石油地球物理勘探, 2004, 39 (4) : 435 –442.
Ling Yun Research Group. Study of seismic resolution limit[J]. Oil Geophysical Prospecting, 2004, 39 (4) : 435 –442. |
| [12] | Vapnik V. The nature of statistical learning theory[M]. New York: Springer, 2000 . |
| [13] |
陈恭洋, 陈玲, 朱洁琼, 等. 地震属性分析在河流相储层预测中的应用[J].
西南石油大学学报:自然科学版, 2012, 34 (3) : 1 –8.
Chen Gongyang, Chen Ling, Zhu Jieqiong, et al. Application of seismic attributes analysis fluvial reservoir to prediction[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2012, 34 (3) : 1 –8. |
| [14] |
伊振林. 井震联合窄小河道砂体预测方法研究[J].
西南石油大学学报:自然科学版, 2012, 34 (1) : 19 –24.
Yi Zhenlin. Prediction method of narrow channel sand body in well-to-seismic integration[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2012, 34 (1) : 19 –24. |
| [15] |
盛海波, 刘蕊, 付国民, 等. 塔河油田3区石炭系超深薄层碎屑岩储层预测研究[J].
地球科学与环境学报, 2011, 33 (4) : 390 –396.
Sheng Haibo, Liu Rui, Fu Guomin, et al. Study on reservoir forecasting for ultra deep thin clastic rock of carboniferous system in Block 3 of Tahe Oilfield[J]. Journal of Earth Sciences and Environment, 2011, 33 (4) : 390 –396. |
| [16] | Li J, Castagna J. Support vector pattern recognition and AVO classification[C]. SEG Annual Meeting, 2003. |
| [17] | Eftekharifar M, Han D H. 3D Petrophysical modeling using complex seismic attributes and limited well log data[C]. SEG Annual Meeting, 2011. |
 2014, Vol. 36
2014, Vol. 36

