2014, Vol. 36引用本文
李雄炎, 秦瑞宝, 刘春成 .岩电参数对储层饱和度计算精度的影响分析[J]. 西南石油大学学报(自然科学版), 2014, 36(3): 68-74.
Li Xiongyan, Qin Ruibao, Liu Chuncheng . Analyzing the Effect of Rock Electrical Parameters on the Calculation of the Reservoir Saturation[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2014, 36(3): 68-74.
岩电参数对储层饱和度计算精度的影响分析 
[PDF全文]
[PDF全文]
中海油研究总院, 北京 东城 100027
摘要: 基于Archie公式, 分析了m, n变化时给饱和度造成的影响, 推导了m, n所携带的误差传递给饱和度的误差公式; 结合疏松砂岩、中等砂岩、致密砂岩、砾岩、凝灰岩、角砾岩、玄武岩、安山岩、英安岩和流纹岩等10种岩性, 阐述了m, n的分布区间、变化幅度及其对计算储层含水饱和度的影响。从而得出在每种岩性内, m的分布范围、变化幅度均大于n, m对饱和度的影响强于n; 当m的误差为±0.2时, 储层含水饱和度的计算误差基本大于5%, 最大值甚至能达到30%;而当n的误差为±0.2时, 储层含水饱和度的计算误差基本小于5%。明确了m, n对饱和度的影响程度及给饱和度传递误差的大小, 对复杂储层饱和度的精确评价具有一定的理论和实践意义。
关键词:
储层评价
Archie公式
岩电参数
饱和度
误差分析
Analyzing the Effect of Rock Electrical Parameters on the Calculation of the Reservoir Saturation
CNOOC Research Institute, Dongcheng, Beijing 100027, China
Abstract: Based on the Archie formula, the effect of variable m and n on the saturation is analyzed, and the error formula of calculating the water saturation of reservoirs caused by the error of m and n is derived. On the basis of the loose sandstone, medium sandstone, tight sandstone, conglomerate, tuff, breccia, basalt, andesite, dacite and rhyolite, this paper first analyzes the distribution range and change amplitude of m and n. Secondly, the impact of m and n on the calculation of the water saturation of reservoirs is discussed. With regard to each lithology, the distribution range and change amplitude of m is greater than those of n. Therefore, compared with n, the effect of m on the saturation is stronger. When the error of m is ±0.2, the error in the calculation of the water saturation of reservoirs is almost all above 5%, and the maximum is even more than 30%. Meanwhile, when the error of n is ±0.2, the error in the calculation of the water saturation of reservoirs is almost all below 5%. The influence of m and n on the saturation is determined, and the error in the calculation of the water saturation of reservoirs caused by the error of m and n are calculated. It is theoretically and practically significant to the precise calculation of saturation of complex reservoirs.
Key words:
reservoir evaluation
Archie formula
rock electrical parameters
saturation
error analysis
在利用电阻率测井资料评价储层饱和度的系列公式中，Archie公式仍然是应用最广泛的公式之一。岩电参数a，b，m和n是Archie公式是否能准确计算储层饱和度的关键参数，特别是碳酸盐岩、火山岩等复杂孔隙结构的储层。一直以来，岩电参数的物理含义、影响因素和计算方法被不同程度地探讨[1-7]，温度、压力、地层水矿化度等因素对岩电参数的影响及岩电参数的计算方法被不同角度地分析[8-12]。另外，从物理含义、影响程度和计算方法3个角度来衡量岩电参数a，b，m和n对储层饱和度的影响，则m，n强于a，b，即m，n具备明确的物理含义、对储层饱和度的影响更大和计算方法相对多样化[13-33]。但m，n所携带的误差究竟对储层含水饱和度传递了多大的误差？二者之间谁对储层饱和度的影响更大？这些问题仍需进一步地明确。因此，本文基于Archie公式，分析了m，n变化时给储层饱和度造成的影响，推导了m，n所携带的误差传递给饱和度的误差公式；并结合疏松砂岩、中等砂岩、致密砂岩、砾岩、凝灰岩、角砾岩、玄武岩、安山岩、英安岩和流纹岩等10种岩性，阐述了m，n的变化幅度及其对计算储层饱和度的影响。定量地评价m，n对计算储层饱和度的影响，有利于利用Archie公式精确地计算复杂孔隙结构储层的饱和度。
1 m对饱和度的影响胶结指数m反映的是岩石的胶结程度，孔径的曲折与级差能反映其值的高低。那么，m的误差会给基于Archie公式计算的储层含水饱和度传递了多大的误差呢？
Archie公式为
| $ {S_{\rm{w}}} = {\left( {\frac{{ab{R_{\rm{W}}}}}{{{\phi ^m}{R_{\rm{t}}}}}} \right)^{1/n}} $ | (1) |
对式（1）两边取对数，得
| $ \ln {S_{\rm{w}}} =-\frac{1}{n}\ln {R_{\rm{t}}}-\frac{m}{n}\ln \phi + \frac{1}{n}\ln \left( {ab{R_{\rm{W}}}} \right) $ | (2) |
式中：a，b—与岩性有关的比例系数，无因次；m—胶结指数，无因次；n—饱和指数，无因次；ϕ—有效孔隙度，%；Rw—地层水电阻率，Ω·m；Rt—含油气岩石电阻率，Ω·m；Sw—含水饱和度，%。
如果式（2）为准确的储层含水饱和度计算公式，那么当m的误差为±0.2时（大多数情况下，m的误差在±0.2内），计算的储层含水饱和度则为
| $ \ln {S_W}' = - \frac{1}{n}\ln {R_{\rm{t}}} - \frac{{m + 0.2}}{n}\ln \phi + \frac{1}{n}\ln \left( {ab{R_{\rm{W}}}} \right) $ | (3) |
当n约为2时（一般情况下，n取2），储层含水饱和度的计算误差如下式
| $ \Delta {S_{\rm{W}}} = \left| {{S_{\rm{W}}}'-{S_{\rm{W}}}} \right| = \left| {\left( {{\phi ^{{\rm{ \pm }}0.1}}-1} \right){S_{\rm{W}}}} \right| $ | (4) |
当有效孔隙度的取值范围为5%~45%，含水饱和度的分布范围为5%~95%时，绘制储层含水饱和度的计算误差（∆Sw），见图 1。
 |
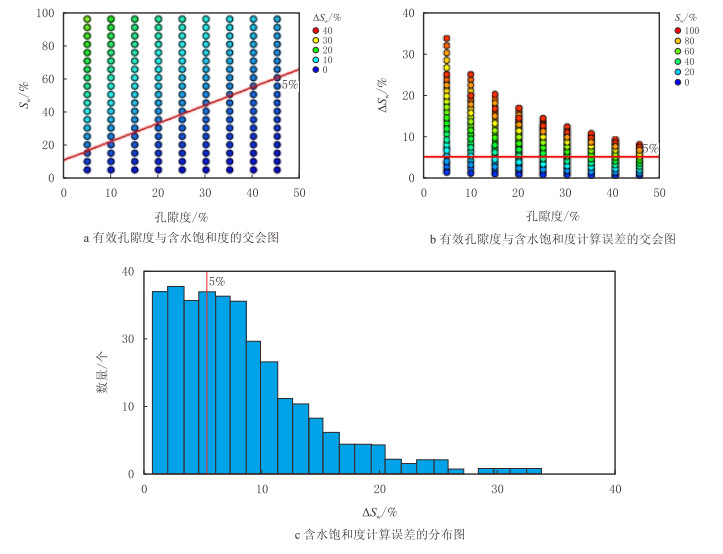| 图1 基于变化m计算储层含水饱和度的误差分布图 Fig. 1 Error distribution in the calculation of the water saturation of reservoirs based on variable m |
按照储量计算的标准，不超过5.00%的饱和度误差为可接受的范围。由图 1可知，在不同类型储层，计算的储层含水饱和度误差的分布范围见表 1。
| 表1 基于变化m计算储层含水饱和度的误差分布范围 Table 1 Error distribution in the calculation of the water saturation of reservoirs based on variable m |
 |
由表 1可知，当m的误差为±0.2时，在有效孔隙度小于15%（低、特低、超低孔储层），含水饱和度分布在20%~60%的储层中，计算的储层含水饱和度误差的分布范围为5.00%~15.00%；而在含水饱和度大于60%的储层中，计算的储层含水饱和度误差的分布范围为10.00%~35.00%；即在低、特低、超低孔储层中，当含水饱和度大于20%时，含水饱和度的计算误差较大，分布范围为5.00%~35.00%。而在低阻储层（一般情况下，低阻储层计算的含水饱和度会偏大，含油气饱和度会偏小），含水饱和度计算误差的分布范围则为5.00%~35.00%。因此，当m的误差为±0.2时，储层含水饱和度的计算误差相对较大，特别是在低孔、低阻等复杂储层中，即m对饱和度的影响相对较大。
2 n对饱和度的影响饱和指数n反映的是岩石的润湿性，与m相比，影响n的因素相对较少，其值也相对稳定，一般取其值为2。那么，n的误差会给基于Archie公式计算的储层含水饱和度传递多大的误差呢？同理，当n的误差为±0.2时，计算的储层含水饱和度的误差为
| $ \Delta {S_{\rm{W}}} = \left| {{S_{\rm{W}}}'-{S_{\rm{W}}}} \right| = \left| {{{\left( {\frac{{ab{R_{\rm{W}}}}}{{{\phi ^m}{R_{\rm{t}}}}}} \right)}^{1/\left( {n{\rm{ \pm }}0.2} \right)}}-{{\left( {\frac{{ab{R_{\rm{W}}}}}{{{\phi ^m}{R_{\rm{t}}}}}} \right)}^{1/n}}} \right| $ | (5) |
对式（5）进行变换，得
| $ \Delta {S_{\rm{W}}} = \left| {{{\left( {\frac{{ab{R_{\rm{W}}}}}{{{\phi ^m}{R_{\rm{t}}}}}} \right)}^{1/n}}\left( {{{\left( {\frac{{ab{R_{\rm{W}}}}}{{{\phi ^m}{R_{\rm{t}}}}}} \right)}^{\frac{{ \mp 0.2}}{{n(n \pm 0.2)}}}}-1} \right)} \right| $ | (6) |
式（6）联立式（1），得
| $ \Delta {S_{\rm{W}}} = \left| {{S_{\rm{W}}}\left( {S_{\rm{W}}^{\frac{{ \mp 0.2}}{{n \pm 0.2}}}-1} \right)} \right| $ | (7) |
当n分别取1.6，1.8，2.0和2.2，含水饱和度的分布范围为5%~95%时，绘制储层含水饱和度的计算误差，见图 2。
 |
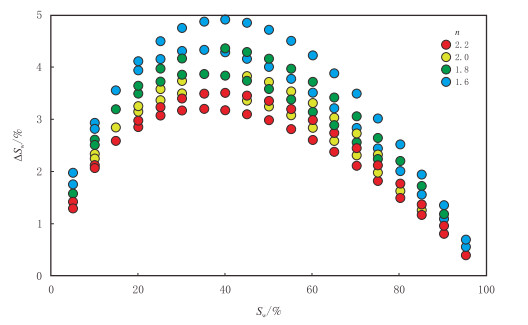| 图2 基于变化n计算储层含水饱和度的误差分布图 Fig. 2 Error distribution in the calculation of the water saturation of reservoirs based on variable n |
由图 2可知，当n在1.6~2.2变化，且其误差为±0.2时，储层含水饱和度的计算误差基本小于5.00%；并且随着n的逐渐变大，储层含水饱和度的计算误差逐渐变小。因此，与m相比，n对饱和度的影响相对较小。
3 实例分析表 2给出了疏松砂岩、中等砂岩、致密砂岩、砾岩、凝灰岩、角砾岩、玄武岩、安山岩、英安岩和流纹岩等10种岩性的孔隙度，m，n的最大值、最小值和平均值。
| 表2 10种岩性相关参数值的分布 Table 2 Parameters of ten kinds of lithologies |
|
图 3、图 4分别是10种岩性m，n的最大值、最小值和平均值的分布图，图 5是m，n的最大值与最小值之间差值的分布图。由图可知，在每种岩性内，m的分布区间、变化幅度均强于n。即岩石组分、孔隙结构的变化对m的影响更大。
 |
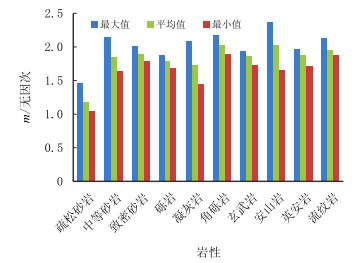| 图3 10种岩性m的分布范围 Fig. 3 Distribution range of m in ten kinds of lithologies |
 |
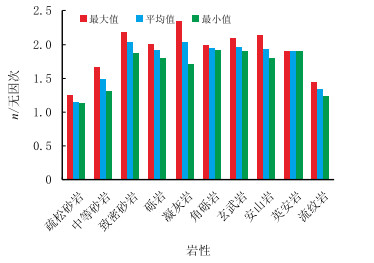| 图4 10种岩性n的分布范围 Fig. 4 Distribution range of n in ten kinds of lithologies |
 |
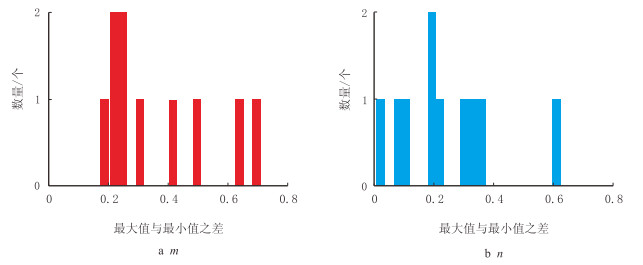| 图5 10种岩性m，n最大值与最小值之差 Fig. 5 Differences between the maximum and the minimum of m and n in ten kinds of lithologies |
结合每类岩石所处的地层环境，确定相应的地层水电阻率和地层真电阻率。基于Archie公式，采用孔隙度的平均值、地层水电阻率和地层真电阻率，在n取平均值时，分别计算m取最大值、最小值和平均值时的含水饱和度；同理，在m取平均值时，分别计算n取最大值、最小值和平均值时的含水饱和度；并分别在m，n变化时，分析各自所计算含水饱和度的平均误差，见表 3。
| 表3 10种岩性计算含水饱和度的平均误差 Table 3 Average errors in the calculation of the water saturation in ten kinds of lithologies |
|
由表 3可知，当m变化时，计算的储层含水饱和度平均误差均大于5.00%；而当n变化时，计算的储层含水饱和度平均误差基本小于5.00%。由于凝灰岩的m、n变化幅度相对较大，m最大值与最小值之差为0.65，基于变化的m所计算的储层含水饱和度的平均误差为29.51%；n最大值与最小值之差为0.62，基于变化的n所计算储层含水饱和度的平均误差为7.23%；m，n变化时，所计算的储层含水饱和度平均误差中的最大值，见图 6。
 |
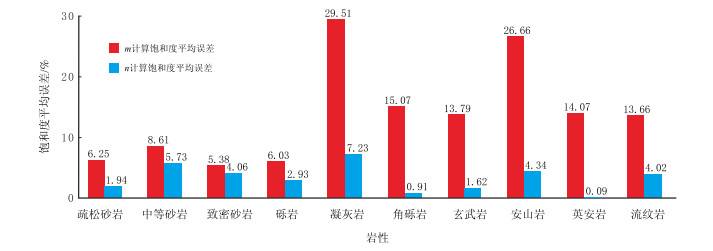| 图6 10种岩性计算含水饱和度的平均误差 Fig. 6 Average errors in the calculation of the water saturation in ten kinds of lithologies |
（1）在每种岩性内，m的分布范围、变化幅度均大于n，m对饱和度的影响强于n。
（2）当m的误差为±0.2时，储层含水饱和度的计算误差基本大于5.00%，其分布范围为5.00%~35.00%，特别是在低孔、低阻等复杂储层中，m对饱和度的影响相对较大。
（3）当n的误差为±0.2时，储层含水饱和度的计算误差基本小于5.00%；当n的误差大于±0.2时，储层含水饱和度的计算误差略大于5.00%。
参考文献
| [1] | Archie G E. The electrical resistivity log as an aid in determining some reservoir characteristics[J]. Petroleum Transactions, AIME, 1942, 146 : 54 –62. DOI:10.2118/942054-G |
| [2] | Marc F, Kholoud A N, Doug B. Water saturation from NMR, resistivity and oil base core in a heterogeneous middle east carbonate reservoir[C]. SPWLA 46th Annual Logging Symposium, 2005. http://www.freepatentsonline.com/6879154.html |
| [3] |
张明禄, 石玉江. 复杂孔隙结构砂岩储层岩电参数研究[J].
测井技术, 2005, 29 (5) : 446 –448.
Zhang Minglu, Shi Yujiang. On Archie's electrical parameters of sandstone reservoir with complicated pore structures[J]. Well Logging Technology, 2005, 29 (5) : 446 –448. |
| [4] |
王勇, 章成广, 李进福, 等. 岩电参数影响因素研究[J].
石油天然气学报, 2006, 28 (4) : 75 –77.
Wang Yong, Zhang Chengguang, Li Jinfu, et al. Study on influence factors of electrical parameters[J]. Journal of Oil and Gas Technology, 2006, 28 (4) : 75 –77. |
| [5] |
赵发展, 王贇, 王界益, 等. 准噶尔和塔里木盆地不同岩性岩电参数研究[J].
地球物理学进展, 2006, 21 (4) : 1258 –1265.
Zhao Fazhan, Wang Yun, Wang Jieyi, et al. Rockelectricity parameters variant lithologic characters in Junggar and Tarim Basins[J]. Progress in Geophysics, 2006, 21 (4) : 1258 –1265. |
| [6] |
罗娜. 阿尔奇公式数值分析及其意义[J].
石油学报, 2007, 28 (1) : 111 –114.
Luo Na. Numerical analysis of Archie formula and its meanings[J]. Acta Petrolei Sinica, 2007, 28 (1) : 111 –114. DOI:10.1111/j.1745-7254.2007.00481.x |
| [7] |
刘向君, 刘洪, 杨超. 碳酸盐岩气层岩电参数实验[J].
石油学报, 2011, 32 (1) : 131 –134.
Liu Xiangjun, Liu Hong, Yang Chao. Experimental study on rock-electricity parameters of carbonate gas reservoirs[J]. Acta Petrolei Sinica, 2011, 32 (1) : 131 –134. |
| [8] | Jean R C. The cementation exponent in the formation factor porosity relation:The effect of permeability[C]. SPWLA 18th Annual Logging Symposium, 1977. https://www.onepetro.org/conference-paper/SPWLA-1977-R |
| [9] | Michael G L, Henry F D, Mukul M S. Wettability and stress effects on saturation and cementation exponents[C]. SPWLA 29th Annual Logging Symposium, 1988. https://www.onepetro.org/conference-paper/SPWLA-1988-K |
| [10] | John C R. A summary of the effects of various pore geometrics and their wettabilities on measured and in-situ values of cementation and saturation exponents[J]. The Log Analyst, 1987, 28 (2) : 1 –25. |
| [11] | Deborah A R. Trends in cementation exponents(m) for carbonate pore systems[J]. Petrophysics, 2002, 43 (5) : 434 –446. |
| [12] | Stalheim S O, Eidesmo T. Is the saturation exponent N A constant?[C]. SPWLA 36th Annual Logging Symposium, 1995. https://www.onepetro.org/conference-paper/SPWLA-1995-SSS |
| [13] | Rasmus J C. A variable cementation exponent M for fractured carbonates[J]. The Log Analyst, 1983, 24 (6) : 13 –23. |
| [14] | Orlando G R. A practical method for determining cementation exponents and some other parameters as an aid in well log analysis[J]. The Log Analyst, 1976, 17 (5) : 8 –24. |
| [15] | Michael M S. The determination of cementation exponents using high frequency dielectric measurements[J]. The Log Analyst, 1983, 24 (6) : 5 –11. |
| [16] | Focke J W, Munn D. Cementation exponents in middle eastern carbonate reservoirs[J]. SPE Formation Evaluation, 1987, 2 (2) : 155 –167. DOI:10.2118/13735-PA |
| [17] | Yuan H H. Advances in apex technology:Determination of cementation exponent and absolute permeability[J]. The Log Analyst, 1991, 32 (5) : 557 –570. |
| [18] | Hilmi S S. Derivation of the cementation factor(Archie's exponent)and the Kozeny-Carman constant from well log data, and their dependence on lithology and other physical parameters[C]. SPE 26309, 1993. |
| [19] | Al-Ghamdi A, Aguilera R, Clarkson C. Cementation exponent estimation for complex carbonate reservoirs using a triple porosity model[C]. SPE/DGS Saudi Arabia Section Technical Symposium and Exhibition, 2011. |
| [20] | Ali Al G, Bo Chen, Hamid B, et al. An improved tripleporosity model for evaluation of naturally fractured reservoirs[J]. SPE Reservoir Evaluation & Engineering, 2011, 14 (4) : 377 –384. |
| [21] | Knackstedt M A, Arns C H, Sheppard A P, et al. Archie's exponents in complex lithologies derived from 3D digital core analysis[C]. SPWLA 48th Annual Logging Symposium, 2007. |
| [22] | Akbar M, Steckhan J, Tamimi M, et al. Estimating cementation factor (m) for carbonates using borehole images and logs[C]. SPE 117786, 2008. |
| [23] | Tabibi M, Emadi M A. Variable cementation factor determination (Empirical Methods)[C]. SPE 81485, 2003. |
| [24] | Kurniawan B, Bassiouni Z. Use of CEC-dependent cementation and saturation exponents in shaly sand resistivity models[C]. SPWLA 48th Annual Logging Symposium, 2007. |
| [25] | Boral A M. A new correlation for the cementation factor in low-porosity carbonates[J]. SPE Formation Evaluation, 1987, 2 (4) : 495 –499. DOI:10.2118/14401-PA |
| [26] | Unalmiser S, Bova J A. A new correlation developed between Archie's parameters and continuous phase change saturation interval[C]. SPE 25514, 1993. |
| [27] | Pairoys F, Al-Zoukani A, Nicot B, et al. Multi-physics approach for aging assessment of carbonate rocks[C]. AlKhobar, Saudi Arabia:SPE/DGS Saudi Arabia Section Technical Symposium and Exhibition, 2011. |
| [28] |
李军, 张超谟, 唐文生, 等. 库车地区致密砂砾岩胶结指数m和饱和度指数n的主要影响因素及其量化研究[J].
石油天然气学报, 2009, 31 (6) : 100 –103.
Li Jun, Zhang Chaomo, Tang Wensheng, et al. Major influential factor and quantitative study on m exponent and n exponent in Kuche Region[J]. Journal of Oil and Gas Technology, 2009, 31 (6) : 100 –103. |
| [29] |
张龙海, 周灿灿, 刘国强, 等. 孔隙结构对低孔低渗储集层电性及测井解释评价的影响[J].
石油勘探与开发, 2006, 33 (6) : 671 –676.
Zhang Longhai, Zhou Cancan, Liu Guoqiang, et al. Influence of pore structures on electric properties and well logging evaluation in low porosity and permeability reservoirs[J]. Petroleum Exploration and Development, 2006, 33 (6) : 671 –676. |
| [30] |
刘兴礼, 张贵斌, 吉云刚, 等. 塔中礁滩型碳酸盐岩储集层测井评价技术[J].
新疆石油地质, 2011, 32 (3) : 321 –324.
Liu Xingli, Zhang Guibin, Ji Yungang, et al. Well logging evaluation technique for reef-flat carbonate reservoir in Tazhong Area, Tarim Basin[J]. Xinjiang Petroleum Geology, 2011, 32 (3) : 321 –324. |
| [31] | Soto Becerra R, Perez O, Arteaga D. A new reservoir classification based on pore types improves characterization[C]. Mexico City, Mexico:SPE Latin America and Caribbean Petroleum Engineering Conference, 2012. |
| [32] | Budebes S, Saif O, Al-Farisi O, et al. Carbonate Archie exponents correction model and variable determination[C]. Abu Dhabi, UAE:SPE Reservoir Characterization and Simulation Conference and Exhibition, 2011. |
| [33] | Asquith G B, Drager L, Saha S. A new approach to estimating Sw in carbonate reservoirs[J]. The Log Analyst, 1993, 34 (3) : 20 –25. |