2. 中国石化华东石油工程有限公司固井分公司, 江苏 扬州 225101
2. Cementing Bureau, East China Company, SINOPEC, Yangzhou, Jiangsu 225101, China
气体钻井技术不仅能减小甚至消除钻井液漏失及卡钻等现象,顺利钻穿水敏性强的泥页岩等层位并保护储层,更能有效提高机械钻速。据统计,在川渝地区采用气体钻井工艺相比常规钻井工艺平均机械钻速提高2~14倍[1]。但相比之下,由于国内对气体钻井的工作特性和工艺参数等研究还不成熟,导致气体钻井比常规钻井时的钻具失效严重[2]。研究表明,气体钻井过程中,气体携岩的上返速度通常在15~100 m/s,气固两相流的冲蚀加之钻柱振动的共同作用是导致钻具疲劳损坏的主要因素[3]。
目前为止,实验成本及其他因素制约导致有关气体携岩冲蚀钻杆,特别是对钻杆接头冲蚀规律的研究相对较少[4-10]。因此,本文根据川东某井的钻井参数,运用计算流体动力学分析了不同偏心程度、不同岩屑颗粒质量流量(或钻速)和不同气体携岩速度(或气体排量)时岩屑颗粒对钻杆接头的冲蚀速率及冲蚀区域分布的规律,为提高钻柱抗冲蚀能力以及可靠性提供参考。
1 气体携岩冲蚀钻杆接头计算模型 1.1 RNGk-ε模型气体携岩从井底经环空返回地面的过程为气-固两相紊流模型。连续相气体可采用RNG k-ε模型描述[11-13],方程如下
| $ \frac{\partial }{{\partial t}}\left( {\rho k} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho k{u_i}} \right) = \frac{\partial }{{\partial {x_j}}}\left( {{\alpha _{\rm{k}}}{\mu _{{\rm{eff}}}}\frac{{\partial k}}{{\partial {x_j}}}} \right) + {G_{\rm{k}}} + {G_{\rm{b}}} - \rho \varepsilon - {Y_{\rm{M}}} + {S_{\rm{k}}} $ | (1) |
| $ \frac{\partial }{{\partial t}}\left( {\rho \varepsilon } \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho \varepsilon {u_i}} \right) = \frac{\partial }{{\partial {x_j}}}\left( {{\alpha _{\rm{\varepsilon }}}{\mu _{{\rm{eff}}}}\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right) + {C_{1{\rm{\varepsilon }}}}\frac{{\rm{\varepsilon }}}{k}({G_{\rm{k}}} + {C_{3{\rm{ \varepsilon }}}}{G_{\rm{b}}}) - {C_{2{\rm{\varepsilon }}}}\rho \frac{{{\varepsilon ^2}}}{k} - R{\rm{\varepsilon }} + {S_{\rm{\varepsilon }}} $ | (2) |
式中:t-时间,s;ρ-气体密度,kg/m3;k-单位质量湍动能,m2/s2;u-速度,m/s;x-位移,m;${\mu _{{\rm{eff}}}}$-有效黏度,Pa·s;$G_{\rm{k}}$-层流速度梯度产生的湍流动能,N/(m2·s);$G_{\rm{b}}$-浮力产生的湍流动能,N/(m2·s);$Y_{\rm{M}}$-由于在可压缩湍流中过渡的扩散产生的波动贡献值,kg/(m$\cdot$s3);C1ε,C2ε,C3ε-常量,无因次;αk,αε-k方程和ε方程的Prandtl数,无因次;ε-单位质量湍动能耗散率,m2/s3;Rε-ε的函数,无因次;Sk,Sε-自定义参数,N/(m2·s)。下标:i,j,k-x,y,z方向。
1.2 随机轨道模型选用随机轨道模型模拟分散相岩屑颗粒在环空中的运行轨迹。随机轨道模型如下
| $ \frac{{{\rm{d}}{u_{\rm{p}}}}}{{{\rm{d}}t}} = {F_{\rm{D}}}\left( {u - {u_{\rm{p}}}} \right) + \frac{{{{\rm{g}}_x}({\rho _{\rm{p}}} - \rho )}}{{{\rho _{\rm{p}}}}} + {F_x} $ | (3) |
| $ \frac{{{\rm{d}}{v_{\rm{p}}}}}{{{\rm{d}}t}} = {F_{\rm{D}}}\left( {v - {v_{\rm{p}}}} \right) + \frac{{{{\rm{g}}_y}({\rho _{\rm{p}}} - \rho )}}{{{\rho _{\rm{p}}}}} + {F_y} $ | (4) |
| $ \frac{{{\rm{d}}{w_{\rm{p}}}}}{{{\rm{d}}t}} = {F_{\rm{D}}}\left( {w - {w_{\rm{p}}}} \right) + \frac{{{{\rm{g}}_z}({\rho _{\rm{p}}} - \rho )}}{{{\rho _{\rm{p}}}}} + {F_z} $ | (5) |
式中:${u_{\rm{p}}}$,${v_{\rm{p}}}$,${w_{\rm{p}}}$-岩屑在x、y、z方向上的速度分量,m/s;u,v,w-气体在x、y、z方向上的速度分量,m/s;${\rm{g}}_x$,${\rm{g}}_y$,${\rm{g}}_z$-x、y、z方向上的重力加速度,9.8 m/s2;${\rho _{\rm{p}}}$,ρ-岩屑密度,气体密度,kg/m3;$F_x$,$F_y$,$F_z$-x、y、z方向上的其他作用力,N;${F_{\rm{D}}}\left({u -{u_{\rm{P}}}} \right)$、${F_{\rm{D}}}\left({v -{v_{\rm{P}}}} \right) $、${F_{\rm{D}}}\left({w -{w_{\rm{P}}}} \right)$-岩屑在x、y、z方向上单位质量曳力,N。
1.3 冲蚀模型气体携带N个岩屑颗粒冲蚀钻杆的冲蚀速率采用以下计算方法[14-15]
| $ {R_{{\rm{ero}}}} = \sum\limits_{n = 1}^{\rm{N}} {\frac{{{{\dot m}_{{\rm{p}}n}}C\left( {{d_{{\rm{p}}n}}} \right)f\left( \alpha \right){v_{{\rm{p}}n}}^{b\left( {{v_{{\rm{p}}n}}} \right)}}}{{{A_{{\rm{wall}}}}}}} $ | (6) |
式中:${R_{{\rm{ero}}}}$-冲蚀速率,kg/(m2·s);$C\left({{d_{{\rm{p}}n}}} \right)$-颗粒直径的函数;$d_{\rm{p}}$-颗粒直径,m;$f\left(\alpha \right)$-颗粒对壁面攻角$\alpha$的函数,rad;$b\left({{v_{{\rm{p}}n}}} \right)$-颗粒相对于壁面速度${v_{{\rm{p}}n}}$的函数,m/s;${A_{{\rm{wall}}}}$-排砂管汇内表面单位冲蚀面积,m2;${{\dot m}_{{\rm{p}}n}}$-岩屑颗粒的质量流量,kg/s;N-最大岩屑颗粒数。
由于钻杆属中碳钢材料,故式(6)中的几个函数可以表示为
| $ \begin{array}{*{20}{l}} {b\left( {{v_{{\rm{p}}n}}} \right) = 1.73}\\ {C\left( {{d_{{\rm{p}}n}}} \right) = 1559B_{\rm{h}}^{ - 0.59}{F_{\rm{s}}} \times {{10}^{ - 7}}} \end{array} $ | (7) |
| $ f\left( \alpha \right) = \left\{ \begin{array}{l} A{\alpha ^2} + B\alpha \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\alpha \theta \\ C{\rm{co}}{{\rm{s}}^2}\alpha {\rm{sin}}\alpha + D{\rm{si}}{{\rm{n}}^2}\alpha + E\;\;\;\alpha > \theta \end{array} \right. $ | (8) |
式中:
${F_{\rm{s}}}$-形状系数,无因次;$B_{\rm{h}}$-钻杆材料的布氏硬度,N/mm2;θ、A、B、C、D、E-常数,取值见表 1。
| 表1 气体携岩冲蚀钻杆模型参数值 Table 1 Value of parameters in erosion model |
以川东X井现场井眼参数为基础,结合上述数学模型,本文建立的计算流体动力学(CFD)模型如图 1所示,气体携岩从底部入口流经环空到达顶部出口。假设井眼为圆形,半径Ro=157.00 mm,钻杆外径Ri1=63.5 mm,加厚接头处外径Ri2=74.6 mm。假设18°斜坡钻杆的截面圆心Oi与井眼截面圆心Oo的距离为偏心距d,并采用结构化网格将钻杆和井眼边界层细化,同时为利于研究冲蚀规律将钻杆接头处网格细化。
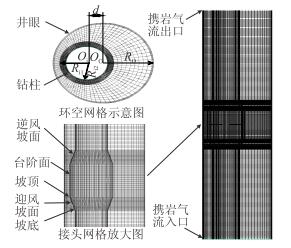 |
| 图1 携岩气体冲蚀钻杆接头部位CFD几何模型及网格 Fig. 1 CFD-geometric model and grid of annual around joint |
根据现场岩屑粒径筛网分析,将有效冲蚀钻柱的岩屑颗粒(直径在0.15~1.50 mm)分为4组,平均粒径为0.62 mm,密度2 300 kg/m3,该区间岩屑颗粒占岩屑总量的70%且质量分布服从Rosin-Rammler规律。
2 气体携岩冲蚀钻杆接头模拟结果在对现场工况进行CFD模拟的基础上,通过改变初始条件来分析不同因素对气体携岩冲蚀钻杆接头速度、岩屑运动轨迹等物理场的影响,以揭示岩屑对钻杆接头冲蚀的规律。
2.1 钻杆无偏心的冲蚀分析当钻杆居中时,无偏心,即d=0,则流场为对称分布。接头的冲蚀速度和气流速度计算结果如图 2所示。气体以40 m/s的速度携岩从模型入口流向接头,计算结果表明,在接头迎风坡面开始发生明显冲蚀现象。由于环空截面面积从接头根部开始减小,导致流道变窄流线改变的同时气流在迎风坡面与台阶面的交界处加速至最大速度52.6 m/s,约为入口速度的1.315倍。岩屑颗粒随着气流方向移动,一部分被气流携带至接头环空,一部分撞击迎风坡面冲蚀接头形成4个冲蚀带并在钻杆和井壁之间形成反复冲蚀。越靠近迎风坡面坡顶,冲蚀速率越大且坡顶附近的冲蚀速率9.69×10-5 kg/(m2·s)是坡底附近冲蚀速率2.42×10-5 kg/(m2·s)的4倍。在两坡面之间的台阶面无明显冲蚀现象。同时,钻杆居中导致接头表面冲蚀速率在距入口同样轴向距离的圆周上均匀分布,主要冲蚀区域呈现圆环状。
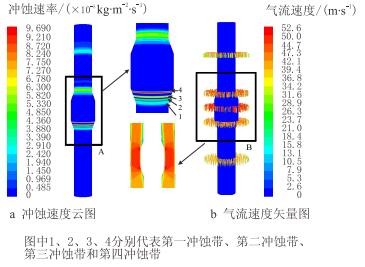 |
| 图2 冲蚀速率与气流速度等值线云图 Fig. 2 Contour map of erosion rate and velocity |
图 3是冲蚀带位置对冲蚀宽度和冲蚀速率影响的关系曲线。由于岩屑颗粒的轨迹随气体流线改变而改变,导致接头处环空的岩屑颗粒分布相比入口更加集中,形成冲蚀带。气体携岩从入口平面均匀入射,并在迎风坡面底部形成涡流,导致第一冲蚀带最宽。其他3个冲蚀带宽度随着离入口距离的增加而减少。相反,冲蚀带内的最大冲蚀速度随着离入口距离的增加而增加并在第四冲蚀带出现钻杆最大冲蚀速率9.69×10-5 kg/(m2·s)。
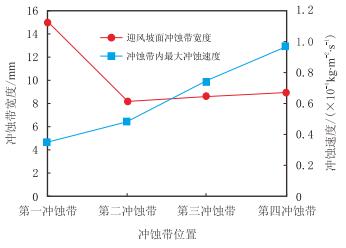 |
| 图3 冲蚀带位置与冲蚀宽度和冲蚀速率的关系 Fig. 3 Relation among erosion zone, width and rate |
由于气体阻尼较小,气体钻井相比泥浆钻井过程中钻柱的横向运动更剧烈,钻杆在井眼内的位置随钻进时间变化而随机改变。钻杆的横向运动必然引起环空中气体携岩流场的变化,最终导致接头不同位置冲蚀速率变化。为了更详细地分析,定义偏心程度为
| $ \delta = \left( {d/s} \right) \times 100\% $ | (9) |
式中:
$\delta$-偏心程度,%;d-偏心距,mm;s-钻杆居中时接箍外径与井眼的间隙,mm;s=82.4。
通过本文建立的CFD模型,其钻杆偏心程度与接头冲蚀区域分布结果如图 4所示,与钻杆居中(无偏心)相比较,偏心导致接头受到不均冲蚀,冲蚀面与入口平面形成一定的夹角,且偏心程度越高,夹角越大,接头冲蚀区域越密集。随着偏心程度的增加,岩屑颗粒在宽通道运移时撞击接头机会减少导致宽通道边逆风面底部冲蚀点开始上移,该侧接头冲蚀区域减少,但最大冲蚀速度大于窄通道冲蚀速率。相反窄通道边的接头冲蚀点开始下移且冲蚀区域更加密集。从偏心20%开始,气体携岩冲蚀台阶面。岩屑颗粒在环空宽流道内聚集导致接头宽流道一侧的冲蚀速率增加,窄流道一侧冲蚀速率减小。
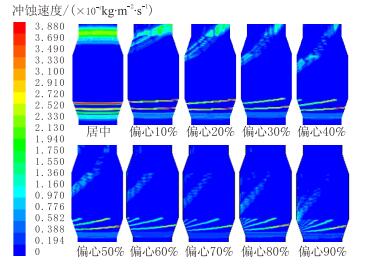 |
| 图4 钻杆偏心程度与接头冲蚀区域分布关系 Fig. 4 Relation between eccentricity and erosion zone |
图 5和图 6分别为不同偏心程度对冲蚀速率、气体速度以及环空岩屑浓度的影响关系曲线。对比图 5和图 6可知,钻杆偏心导致携岩气体流场和岩屑浓度分布发生改变,且钻杆偏心程度不同导致影响接头宽流道和窄流道两侧冲蚀速率的主要因素不同。随着钻杆偏心程度的增加,窄流道一侧接头冲蚀速率和钻杆最大冲蚀速率的分布规律呈现整体增加的趋势。宽流道一侧接头的冲蚀速率在偏心程度80%内随钻杆偏心程度的增加逐渐减小,80%之后随偏心程度增加而增加。从图 5可知,钻杆偏心30%内,接头宽流道环空的岩屑浓度随偏心程度增加而增加。当钻杆偏心程度继续增加时,宽流道环空岩屑浓度基本保持恒定。在钻杆偏心70%时岩屑浓度达到极值0.432 kg/m3,约是窄流道环空岩屑浓度0.156 kg/m3的3倍。当钻杆偏心30%~50%和70%~80%时,岩屑的浓度(N)对冲蚀速度起主导作用,并随着接头宽流道环空岩屑浓度的减小而减小。而如图 6所示,钻杆偏心程度为0~30%、50%~70%和80%~90%时,窄流道速度(v)增加导致接头冲蚀速率增加,此偏心程度内携岩速度对接头冲蚀速率起主导作用。
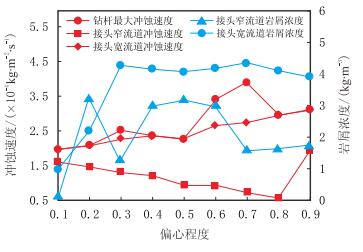 |
| 图5 偏心程度对冲蚀速率和岩屑浓度的影响 Fig. 5 Impact of eccentricity on erosion rate and concentration of cuttings |
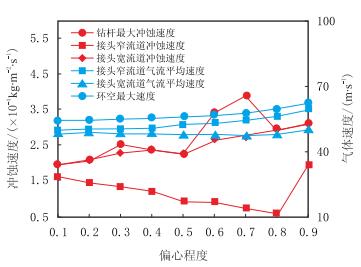 |
| 图6 偏心程度对冲蚀速率和气体速度的影响 Fig. 6 Impact of eccentricity on erosion rate and velocity |
注气量和机械钻速的不同直接影响气体携岩时的速度和岩屑含量。气流携岩速度和岩屑含量的改变势必改变接头冲蚀规律。在钻杆居中模拟的基础上将注气量换算成气体携岩速度,分别设置为40,60,80 m/s,钻速分别设置为3.6,7.2,11.5,14.4,20.0 m/h。表 2为钻速及其相应质量流量的关系。
| 表2 钻速与岩屑质量流量关系 Table 2 Relation between drilling rate and mass flow rate of cuttings |
采用本文建立的CFD模型,同时设置上述入口条件,其计算结果如图 7所示。当钻杆偏心程度为0,气流携岩速度40 m/s时,岩屑质量流量越大,同一冲蚀带宽度越窄。携岩速度相同,接头最大冲蚀速度随着岩屑质量流量增加线性增加。岩屑质量流量为0.989~474 kg/s时接头最大冲蚀速率是岩屑质量流量为0.178~105 kg/s时的5.6倍。岩屑质量流量相同时,携岩速度80 m/s和60 m/s时,接头的最大冲蚀速率分别为携岩速度40 m/s时的2.0倍和3.3倍。
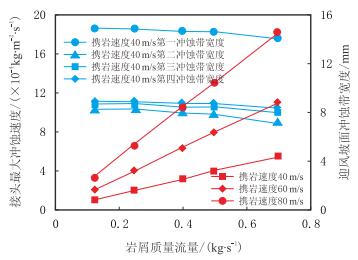 |
| 图7 岩屑质量流量对接头最大冲蚀速率和迎风坡面冲蚀带宽度的影响 Fig. 7 Impact of mass flow rate on maximum erosion rate and erosion width of windward slope |
本文研究结果已在川东X井邻井得到了应用和验证,与现场数据基本吻合,对类似井况的钻杆接头冲蚀预测具有一定的参考和指导意义。
3 结论(1) 钻杆居中时,物理场呈对称分布,主要冲蚀区域呈圆环状。随着接头迎风坡面与入口面轴向距离的增加,冲蚀速率增大;同时,在坡面顶部附近出现最大冲蚀速率。相比钻杆本体,接头冲蚀更严重。携岩速度相同时,接头最大冲蚀速率随岩屑质量流量增加线性增加,岩屑质量流量相同时,携岩速度越大接头冲蚀速率越大。
(2) 钻杆偏心时的最大冲蚀速率和接头宽流道一侧的冲蚀速率比钻杆居中时大。冲蚀面与入口平面形成一定的夹角,且偏心程度越高,夹角越大,接头窄流道一侧冲蚀区域越密集。不同的主导因素导致不同偏心程度接头的冲蚀速率不同:钻杆偏心0~30%、50%~70%和80%~90%时,接头冲蚀速率随携岩速度增加而增加;当钻杆偏心30%~50%和70%~80%时,接头冲蚀速率随接头宽流道环空岩屑浓度的减小而减小;当钻杆偏心30%、60%、70%时,最大冲蚀速率由接头宽流道一侧转移至钻杆本体。
| [1] |
艾惊涛, 余锐, 廖兵, 等. 四川油气田气体钻井技术现状及发展方向[J].
天然气工业, 2009, 29 (7) : 39 –41.
Ai Jingtao, Yu Rui, Liao Bing, et al. The status quo and future development of gas drilling technology in the Sichuan Gas Field[J]. Natural Gas Industry, 2009, 29 (7) : 39 –41. |
| [2] |
苏义脑, 周川, 窦修荣. 空气钻井工作特性分析与工艺参数的选择研究[J].
石油勘探与开发, 2005, 32 (2) : 86 –90.
Su Yinao, Zhou Chuan, Dou Xiurong. Operation characteristics analysis and process parameters selection of air drilling[J]. Petroleum Exploration and Development, 2005, 32 (2) : 86 –90. |
| [3] | 林铁军.气体钻井钻具失效机理研究[D].成都:西南石油大学, 2009. |
| [4] |
祝效华, 刘少胡, 童华. 气体钻井钻杆冲蚀规律研究[J].
石油学报, 2010, 31 (6) : 1013 –1017.
Zhu Xiaohua, Liu Shaohu, Tong Hua. A study on the drill pipe erosion law in gas drilling[J]. Acta Petrolei Sinica, 2010, 31 (6) : 1013 –1017. |
| [5] |
练章华, 魏臣兴, 宋周成, 等. 高压高产气井屈曲管柱冲蚀损伤机理研究[J].
石油钻采工艺, 2012, 34 (1) : 6 –9.
Lian Zhanghua, Wei Chenxing, Song Zhoucheng, et al. Erosion damage mechanism of buckled tubing in high pressure and high production gas wells[J]. Oil Drilling & Production Technology, 2012, 34 (1) : 6 –9. |
| [6] |
刘文红, 李磊, 刘永刚, 等. 基于流场分析的钻杆内加厚过渡带管冲蚀失效机理[J].
中国腐蚀与防护学报, 2011, 31 (2) : 160 –164.
Liu Wenhong, Li Lei, Liu Yonggang, et al. Mechanism of erosion-corrosion washout failure in internal upset transition zone for drillpipe based on application of flow field analysis[J]. Journal of Chinese Society for Corrosion and Protection, 2011, 31 (2) : 160 –164. |
| [7] |
黄小兵, 刘清友. 基于气体钻井工艺参数的钻具冲蚀模型[J].
石油学报, 2012, 33 (5) : 878 –880.
Huang Xiaobing, Liu Qingyou. An erosion model of drill string based on process parameters of gas drilling[J]. Acta Petrolei Sinica, 2012, 33 (5) : 878 –880. |
| [8] |
林铁军, 练章华, 陈世春, 等. 气体钻井中气体携岩对钻杆的冲蚀机理研究[J].
石油钻采工艺, 2010, 32 (4) : 1 –4.
Lin Tiejun, Lian Zhanghua, Chen Shichun, et al. Study on drill pipe erosion of gas carrying cuttings in gas drilling[J]. Oil Drilling & Production Technology, 2010, 32 (4) : 1 –4. |
| [9] |
朱红钧, 林元华, 李强, 等. 空气钻井井眼净化与冲蚀效应模拟分析[J].
断块油气田, 2010, 17 (6) : 765 –768.
Zhu Hongjun, Lin Yuanhua, Li Qiang, et al. Numerical simulation of hole cleaning and erosion effect for air drilling[J]. Fault-Block Oil & Gas Field, 2010, 17 (6) : 765 –768. |
| [10] |
郭建华, 佘朝毅, 李黔, 等. 气体钻井井筒冲蚀作用定量分析及控制方法[J].
石油学报, 2007, 28 (6) : 129 –132.
Guo Jianhua, She Chaoyi, Li Qian, et al. Quantitative analysis and controlling method for pipe string erosion in gas drilling[J]. Acta Petrolei Sinica, 2007, 28 (6) : 129 –132. |
| [11] |
丁珏, 翁培奋. 90°弯管内流动的理论模型及流动特性的数值研究[J].
计算力学学报, 2004, 21 (3) : 314 –321.
Ding Jue, Weng Peifen. Numerical simulation of theoretical models & flow characteristics in 90° bending duct[J]. Chinese Journal of Computational Mechanics, 2004, 21 (3) : 314 –321. |
| [12] |
袁新明, 贺治国, 毛根海. 用RNG k-ε紊流模型对截止阀三维紊流流动的数值模拟[J].
流体机械, 2006, 34 (2) : 34 –38.
Yuan Xinming, He Zhiguo, Mao Genhai. Numerical simulation of a turbulence flow in the cut-off valve by RNG k-ε turbulence model[J]. Fluid Machinery, 2006, 34 (2) : 34 –38. |
| [13] |
刘涛, 李风婷, 景雪辉. T型管接头的流固耦合及热应力分析[J].
机床与液压, 2010, 38 (3) : 127 –128.
Liu Tao, Li Fengting, Jing Xuehui. The T-tube joint fluidsolid coupling and thermal stress analysis[J]. Machine Tool & Hydraulics, 2010, 38 (3) : 127 –128. |
| [14] | Edwards J K, McLaury B S, Shirazi S A. Modeling solid particle erosion in elbows and plugged tees[J]. Journal of Energy Resources Technology, 2001, 123 (4) : 277 –284. DOI:10.1115/1.1413773 |
| [15] | Nøkleberg L, Søntvedt T. Erosion of oil & gas industry choke valves using computational fluid dynamics and experiment[J]. International Journal of Heat and Fluid Flow, 1998, 19 (6) : 636 –643. DOI:10.1016/S0142-727X(98)10039-5 |
 2014, Vol. 36
2014, Vol. 36

