2. "油气藏地质及开发工程"国家重点实验室·西南石油大学, 四川 成都 610500
2. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitaion, Southwest Petroleum University, Chengdu, Sichuan 610500, China
页岩气高效开发的关键技术主要有低成本的水平井钻井技术+多段压裂技术、清水压裂技术和压裂技术-同步压裂技术,这些先进的技术不断提高页岩气井的产量,正是这些先进技术的成功应用,促进了美国页岩气开发的快速发展[1]。美国Barnett页岩气开发实践表明,对于位移不大、储层均质性较好、难度一般的水平井钻井,在常规液相钻井液条件下,主要采用常规马达导向的钻井技术[2],一般导向钻井下部钻具组合(BHA)由高效钻头+导向马达+稳定器+MWD组成,而由于页岩气水平井钻井中摩阻/扭矩控制、轨迹控制和携岩要求的特殊性,页岩气水平井钻井下部钻具组合常采用欠尺寸稳定器,这种导向钻井技术既能在转盘不动情况下实现滑动定向钻进,又能在转盘旋转情况下实现复合钻进,从而达到连续控制井眼轨迹的目的,可一趟钻完成增斜、稳斜、降斜和扭方位等定向作业[3]。欠尺寸稳定器在页岩气钻井中起着比较重要的作用,欠尺寸稳定器是一种整体式螺旋稳定器,即稳定片是螺旋形的,这种结构的稳定器蹩劲小[4]。在页岩气水平井钻井中,欠尺寸螺旋稳定器不仅具有控制井眼轨迹的作用,而且还有助于降低摩阻/扭矩、减少钻具阻卡的风险和改善井眼清洁状况等[5-11]。为此,本文将采用数值模拟的方法,模拟欠尺寸螺旋稳定器环空流场特性,以揭示其改善井眼清洁的作用机理和工作原理。
1 环空流场分析数学模型由于环空钻井液黏度较大,不能视为理想无黏性流体,黏性是流体受外力作用移动时内摩擦力的表现,一般流动速度梯度越大摩擦力越大,而且稳定器环空存在速度梯度较大的区域,因此,在进行环空流场分析时必须考虑钻井液黏性力的作用。另外,由于在稳定器环空几何形状极不规则,使得流体流动结构往往呈湍流状态。湍流与层流相比,湍流流动结构极不规则而且十分复杂,也就无法采用数学模型进行流场的分析和计算,这使得湍流与层流相关计算存在本质上的差异,对层流问题只需对流动控制方程进行求解,而对湍流问题却无法采用这些直接求解的方法,只能采用数值计算方法,比如紊流黏性模型法、直接计算法、大涡模拟法等,对于本文研究的稳定器环空这种高度复杂的三维流动,选择湍流问题计算中应用较为广泛的紊流黏性模型方法。对流动结构不规则的湍流流动,求解湍流瞬时的流动情况对工程实际意义不大,因此,可以对湍流流动参数进行适当的统计处理,即通常所说的平均法,平均法有时均、体均、概率平均3种方法,本文采用时均法。为此,对瞬时的连续方程与动量方程进行时均处理,去掉平均速度上的横线,可把连续方程与动量方程写成笛卡儿坐标系下的张量形式[12-13]
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}(\rho {u_i}) = 0 $ | (1) |
| $ \begin{array}{l} \rho \frac{{{\rm{d}}{u_i}}}{{{\rm{d}}t}} = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left[{\mu \left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}-\frac{2}{3}{\delta _{ij}}\frac{{\partial {u_l}}}{{\partial {x_l}}}} \right)} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\partial ( - \rho \overline {{{u'}_i}{{u'}_j}} )}}{{\partial {x_j}}} \end{array} $ | (2) |
式中:$\rho$-钻井液密度,g/cm3;$t$-时间,s;$u$-时均速度,m/s;$p$-流体微元上的时均压力,Pa;$\mu$-动力黏度系数,kg/(m·s);${\delta _{ij}}$-Kronecker符号;$ \overline{u'}_i$,$\overline{u'}_j$-脉动速度,m/s;下标i,j,l=1,2,3,对应于x轴,y轴,z轴3个坐标方向;
式(1)和式(2)称为雷诺平均的N-S方程。它与瞬时N-S方程具有相同的形式,只是速度或其他求解变量变成了时间平均量。N-S方程经时间平均,成为对非线性项易处理的形式,但由于出现了雷诺应力项
| $ \begin{array}{l} \rho \frac{{{\rm{d}}k}}{{{\rm{d}}t}} = \frac{\partial }{{\partial {x_j}}}\left[{\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _{\rm{k}}}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{G_{\rm{k}}} + {G_{\rm{b}}} - \rho \varepsilon - {Y_{\rm{M}}} \end{array} $ | (3) |
| $ \begin{array}{l} \rho \frac{{{\rm{d}}\varepsilon }}{{{\rm{d}}t}} = \frac{\partial }{{\partial {x_j}}}\left[{\left( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \rho {{\rm{C}}_1}E\varepsilon - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\rho {{\rm{C}}_2}\frac{{{\varepsilon ^2}}}{{k + \sqrt {\nu \varepsilon } }} + {{\rm{C}}_{1\varepsilon }}\frac{\varepsilon }{k}{{\rm{C}}_{3\varepsilon }}{G_{\rm{b}}} \end{array} $ | (4) |
其中:
| $ {C_1} = \max \left[{0.43, \frac{\eta }{{\eta + 5}}} \right] $ | (5) |
| $ \eta = {(2{E_{ij}} \cdot {E_{ji}})^{1/2}}\frac{k}{\varepsilon } $ | (6) |
| $ {E_{ij}} = \frac{1}{2}({u_{i, j}} + {u_{j, i}}) $ | (7) |
式中:k-单位质量湍动能,m2/s2;
$\mu_{\rm t}$-湍动黏度,Pa·s;
$\sigma_{\rm k}$-湍动能的湍流普朗特数,无因次,$\sigma_{\rm k}$=1.0;
$G_{\rm k}$-平均速度梯度引起的湍动能产生项,N/(m2$\cdot$s);
$G_{\rm b}$-浮力影响引起的湍动能产生项,N/(m2$\cdot$s);
ε-单位质量湍动耗散率,m2/s3;
$Y_{\rm M}$-可压缩湍流脉动膨胀对总耗散率的影响,kg/(m·s3);
σε-湍动耗散率的湍流普朗特数,无因次,σε=1.20;
C1,C1ε,C2-经验常数,无因次,C1ε=1.44,C2=1.90;
$\nu$-运动黏度系数,m2/s;
C3ε-浮力对耗散率的影响,流动与重力方向相同时C3ε=1,流动与重力方向垂直C3ε=0;
E-时均应变率,s-1。
Realizable k-ε湍流模型适合的流动类型比较广泛,包括有旋均匀剪切流、自由流(射流和混合层)、腔道流动和边界层流动,Realizable k-ε模型对强旋流动计算具有较高的精度[5-12]。对上述稳定器环空流场的计算,采用有限体积法,对方程组求解采用压力修正法中的SIMPLE算法(Semi-Implicit Method for Pressure-linked Equations,即半隐式压力相关方程解法)进行压力速度耦合,并离散为二阶迎风格式。
2 环空流场模型的建立 2.1 稳定器结构稳定器的作用是在钻柱高速回转时,保持细长钻杆平稳运转,使钻头轴线尽可能接近井眼中心线,从而减轻钻柱在井眼径向和轴向的剧烈振动,减少钻头和钻杆偏磨,防止井斜或用于人工定向钻进。稳定器的结构比较简单,是带有肋骨片(直条或螺旋形)的粗径接头。本文所述的欠尺寸稳定器是一种整体式螺旋稳定器,即稳定片是螺旋形的,其结构如图 1所示[4-18]。在定向井、水平井中使用这种稳定器时,在螺旋稳定片处过流面积减小,增强了钻井液对岩屑的冲刷作用;同时,由于螺旋稳定片在旋转时可以使流场产生循环力和陀螺力,搅动岩屑,并对被搅动的岩屑有支承作用,有利于岩屑床的清除。
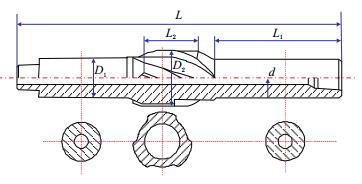 |
| 图1 欠尺寸螺旋稳定器结构 Fig. 1 The structure of under-size spiral stabilizer |
仿真模型参数:
(1) 井眼直径为ϕ215.9 mm,井壁的绝对粗糙度为0.5 mm;
(2) 欠尺寸螺旋稳定器的稳定片直径D2=208.0 mm,稳定器本体接头外径D1=178.0 mm,螺旋扶正块数量为3个,螺旋升角为70°,螺旋带长度L2=600 mm,假设稳定器壁面绝对粗糙度为0.046 78 mm;
(3) 研究管段取稳定器以上5 000 mm,稳定器以下3 000 mm的一段环空流体域进行模拟分析;
(4) 钻井液密度1.30 g/cm3,黏度47.00 mPa·s,岩屑密度为2.50 g/cm3,岩屑体积含量为0.05%,岩屑颗粒直径为0.5 mm。据此几何尺寸建立了欠尺寸稳定器流体力学分析物理模型,如图 2a,图 2b,图 2c,图 2d所示。对所建立的物理模型采用六面体单元划分体网格,形成的网格如图 2e,图 2f,图 2g,图 2h所示。数值仿真计算时,所设置边界条件为:钻井液与岩屑流混合物从环空底部入口进入,入口体积流量为30.00 L/s,固相颗粒流速为1.00 m/s;钻井液从环空顶部流出,出口边界定义为压力出口,此处定义压力出口为2 000 m井深条件下的环空压力25.00 MPa;定义井壁、稳定器和钻铤壁面为无穿透固定边界。
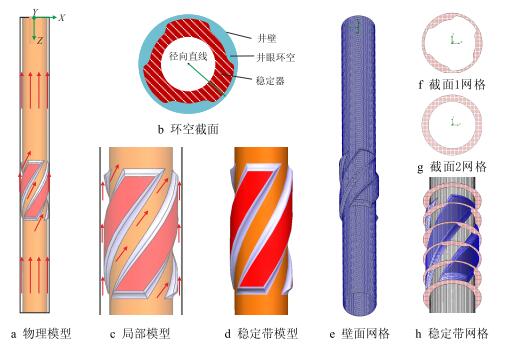 |
| 图2 欠尺寸螺旋稳定器环空流场仿真模型 Fig. 2 The simulation model of annulus flow field for under-size spiral stabilizer |
通过数值模拟分析,计算出了欠尺寸螺旋稳定器环空螺旋槽流场的速度场、压力场特性,图 3所示为钻井液在欠尺寸螺旋稳定器环空流动的流速分布云图,图中包括所研究环空流道的流速分布剖面图、全局图和截面图。
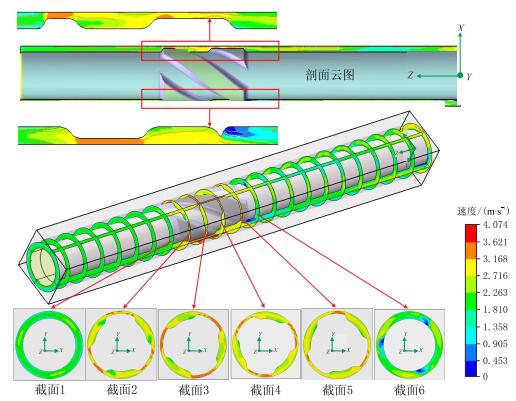 |
| 图3 稳定器环空流速分布 Fig. 3 The velocity distribution in stabilizer annulus |
由图 3中的剖面图和局部放大视图不难看出,在稳定器流场上游(迎流端)流速分布相对均匀,在靠近稳定器位置,流速分布开始发生扰动,如图 3中截面1所示。在稳定器外侧环空,当钻井液从钻铤环空进入稳定片环空时,由于压差和过流截面减小的作用,流速由钻铤环空的1.910 m/s增加至4.070 m/s;当钻井液从稳定片环空再次进入钻铤环空时,由于过流截面恢复,流速由钻铤环空的4.070 m/s降低至2.450 m/s;即钻井液流速历经了由小变大再减小的过程;而且,钻井液流速在稳定器稳定片外侧的流速较高(约为3.620 m/s),在稳定器螺旋槽内流速稍低(约为3.110 m/s);稳定器外侧的流速分布极不均匀,流动结构也极其混乱,一般靠近稳定器壁面流速较低,靠近井壁流速较高。由图 3中截面1~6可以看出,环空流速场呈现出3个轴对称的等速流动区,等速流动区中的流速分布与稳定片和轴向位置的关系密切;在靠近稳定片的中上游,等速流动区中的高流速区偏向于稳定带外侧的窄间隙(图 3截面2~4);在靠近中下游(背流端)等速流动区的高速区分布在稳定器稳定片螺旋升角左侧的窄间隙(图 3截面5),而稳定器螺旋槽内流速相对较低;当流过稳定器,再次进入钻铤环空时,在稳定器流场下游流速分布受稳定器扰动的原因,其流速场分布也极不均匀,在靠近稳定器位置,即稳定片斜坡末端出现了低速流动区(死区),该区流体基本不流动,这是由于环空流体在从稳定器处再次进入环空时,在稳定片末端的斜坡属于流动背流面,流体进入该区域时将形成绕流和漩涡流动。
图 4为环空稳定器环空剖面内流速矢量图。从图 4看出,在整个稳定器环空和上部的钻铤环空内,由于稳定器结构特殊性,使得环空流场存在大量的漩涡流动。在螺旋槽左侧的稳定片外侧环空处出现了较强的漩涡流动,漩涡流动处的流速分布差异极大;另外剖面内流速矢量分布也呈现出3个轴对称分布区域。
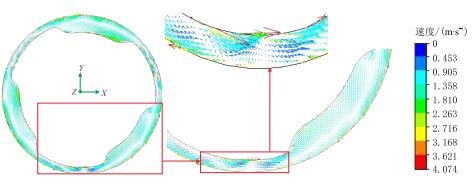 |
| 图4 稳定器环空剖面内流速矢量图 Fig. 4 The velocity vector in section of stabilizer annulus |
漩涡流动的存在也可以从图 5所示的稳定器环空涡量分布云图看出,涡量定义为速度场的旋度,在流体中只要有“涡量源”,就会产生涡旋。在稳定器环空下端(入口段)涡量比较小,只是在靠近井壁位置的涡量较大,这是由于井壁粗超度较大所致;在稳定器段及上部环空段,流场的涡量均比较大,这主要是由稳定器螺旋结构特殊所决定,螺旋结构所导致的漩涡流动与井眼尺寸大小、稳定器螺旋带外径、稳定器本体外径、螺旋带数量、螺旋升角、螺旋带长度、排量、偏心度、转速、井深等多种因素有关,其中,受螺旋带数量、螺旋升角、螺旋带长度、偏心度等因素的影响较大,漩涡流动将诱发动压力的产生。
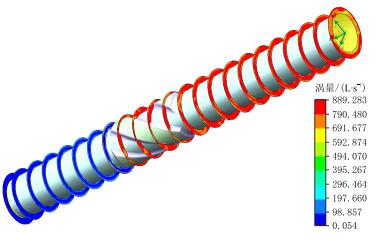 |
| 图5 稳定器环空涡量分布 Fig. 5 The vorticity distribution in stabilizer annulus |
图 6所示为钻井液在欠尺寸螺旋稳定器环空流动的总压力分布云图。由图 6可以看出,螺旋稳定器形状不规则所引起的压力扰动在稳定器流场上下游(迎流端和背流端)差异较大,稳定器上下游压差约为0.03 MPa左右。在稳定带外侧环空出现了明显的绕流现象,使得压力场也发生了显著的改变(如图 6截面2~5),环空压力场呈现出3个轴对称的等压区,等压区中的分布与稳定带和轴向位置的关系密切。在靠近上游(迎流端)等压区中的高压偏向于稳定带外侧(如图 6截面2~3);在靠近中下游(背流端)等压区的高压分布在稳定器螺旋槽右旋侧,而稳定带外侧趋于形成低压区;当流过稳定带,再次进入钻铤环空时,在靠近稳定带附近压力分布也呈现出不均匀分布,此时的环空压力场分布也基本呈现出3个轴对称的等压区,其中核心区为高压区,周围为低压区,而且等压区的分布受螺旋升角的影响,即等压区呈螺旋状发展,这便形成了有利于清除岩屑的螺旋冲刷流动;当远离稳定带一定距离(约4 m),稳定带所形成的螺旋流压力场分布特性逐渐减弱,环空逐渐恢复稳定流动。另外,计算条件下的压降约为0.03 MPa,压力损失比较小,以井下环空压力为25.00 MPa计算,此处压降约为环空压力的0.12%,基本上可以忽略。
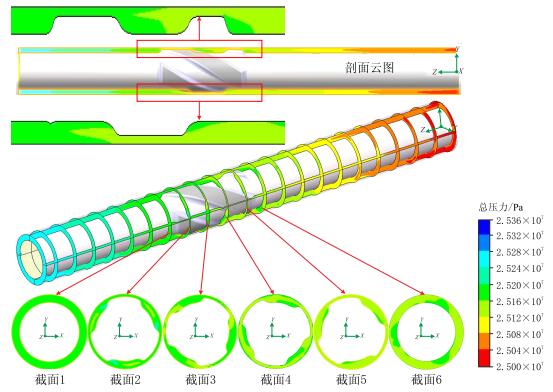 |
| 图6 稳定器环空总压力分布 Fig. 6 The total pressure distribution in stabilizer annulus |
图 7所示为钻井液在欠尺寸螺旋稳定器环空流动的动压力分布云图。由图 7可以看出,由于稳定器外侧螺旋槽附近及下游产生了大量的漩涡流动,所产生的的漩涡流动会在该处引起强烈的压力波动(如图 7截面2~6),计算条件下的动压力为0.014 MPa。环空动压力分布也呈现出了3个轴对称的等压区,等压区的分布状态与稳定带和轴向位置的关系密切,其分布规律与压力场分布规律基本类似。循环状态下的动压力是诱发钻柱振动的激振力之一,激振力的大小与井眼尺寸大小、稳定器螺旋带外径、稳定器本体外径、螺旋带数量、螺旋升角、螺旋带长度、排量、偏心度、转速、井深等多种因素有关,激振力过大会诱发钻柱发生高频横向振动。
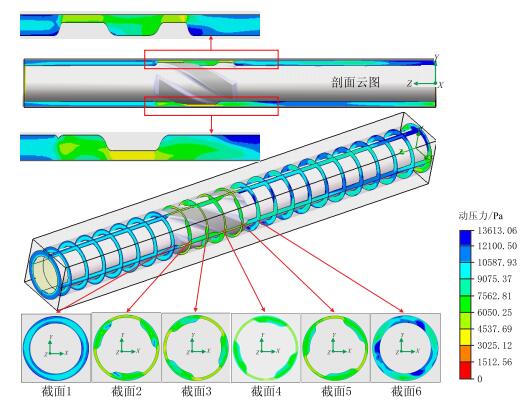 |
| 图7 稳定器环空动压力分布 Fig. 7 The dynamic pressure distribution in stabilizer annulus |
(1) 在欠尺寸稳定器环空流场的上游段(入口段)环空流速、压力分布相对均匀,流动迹线基本近似平行,该段流场的涡量也较小,上游段的压力、流速扰动主要是由于井壁不规则所致,但是在靠近稳定器位置,由于稳定器结构原因流速和压力的分布开始出现扰动。
(2) 在欠尺寸稳定器环空流场的中下游段(稳定器外环空和出口段)环空流速、总压力和动压力的分布均出现了3个轴对称的流动区域(即等压流动区、等速流动区和动压等压区),该流动区域的形成、发展和分布规律基本呈螺旋状,与距离稳定片位置、轴向位置、稳定器尺寸、排量等参数关系密切,这种螺旋流动状态对于清除井壁岩屑床十分有利。
(3) 稳定器段及上部环空段,流场的涡量均比较大,流动迹线也发展为极不规律的交叉曲线,而且呈螺旋绕流形式,这主要是由稳定器螺旋结构特殊所决定,稳定器的螺旋结构导致流体发生绕流,绕流时形成了大量的漩涡流动,伴随产生了较大的动压力,而动压力诱发的激振力会加剧钻柱振动。
| [1] |
崔思华, 班凡生, 袁光杰. 页岩气钻完井技术现状及难点分析[J].
天然气工业, 2011, 31 (4) : 72 –75.
Cui Sihua, Ban Fansheng, Yuan Guangjie. Status quo and challenges of global shale gas drilling and completion[J]. Natural Gas Industry, 2011, 31 (4) : 72 –75. |
| [2] |
唐代绪, 赵金海, 王华, 等. 美国Barnett页岩气开发中应用的钻井工程技术分析与启示[J].
中外能源, 2011, 16 (4) : 47 –52.
Tang Daixu, Zhao Jinhai, Wang Hua, et al. Technology analysis and enlightenment of drilling engineering applied in the development of Barnett shale gas in America[J]. Sino-global Energy, 2011, 16 (4) : 47 –52. |
| [3] |
周文军, 欧阳勇, 黄占盈, 等. 苏里格气田水平井快速钻井技术[J].
天然气工业, 2013, 33 (8) : 77 –82.
Zhou Wenjun, Ouyang Yong, Huang Zhanying, et al. Rapid drilling technologies of horizontal wells in the Sulige Gas Field, Ordos Basin[J]. Natural Gas Industry, 2013, 33 (8) : 77 –82. |
| [4] | 陈平. 钻井与完井工程[M]. 北京: 石油工业出版社, 2011 : 184 -185. |
| [5] |
陈锋, 狄勤丰, 袁鹏斌, 等. 高效岩屑床清除钻杆作用机理[J].
石油学报, 2012, 33 (2) : 298 –303.
Chen Feng, Di Qinfeng, Yuan Pengbin, et al. Mechanism of an effective hydroclean drill pipe for hole cleaning[J]. Acta Petrolei Sinica, 2012, 33 (2) : 298 –303. |
| [6] | Sifferman T R, Becker T E. Hole cleaning in full-scale inclined wellbores[J]. SPE Drilling Engineering, 1992, 7 (2) : 115 –120. DOI:10.2118/20422-PA |
| [7] | Van Puymbroeck L, Williams H. Increasing drilling performance for ERD wells using new generation hydromechanical drill oipe[J]. AADE-13-FTCE-01, 2013 . |
| [8] | Ahamed R, Sagheer M, Takach N. Experimental studies on the effect of mechanical cleaning devices on annular cuttings concentration and application for optimizing ERD systems[C]. SPE 134269, 2010. http://www.doc88.com/p-678404561850.html |
| [9] |
石晓兵. 大位移井中利用钻柱旋转作用清除岩屑床的机理研究[J].
天然气工业, 2000, 20 (2) : 51 –53.
Shi Xiaobing. A study of the mechanism to remove cuttings bend in extended reach well by utilizing rotation action[J]. Natural Gas Industry, 2000, 20 (2) : 51 –53. |
| [10] |
王瑞和, 李明忠, 王成文, 等. 油气井注水泥顶替机理研究进展[J].
天然气工业, 2013, 33 (5) : 1 –8.
Wang Ruihe, Li Mingzhong, Wang Chengwen, et al. Research progress in the cementing displacement mechanism[J]. Natural Gas Industry, 2013, 33 (5) : 1 –8. |
| [11] |
舒秋贵. 在旋流扶正器作用下环空流场旋流衰减规律研究[J].
天然气工业, 2005, 25 (9) : 57 –60.
Shu Qiugui. Research on the helical flow attenuation law in annular flow field by the action of cyclone centralizer[J]. Natural Gas Industry, 2005, 25 (9) : 57 –60. |
| [12] |
刘伟, 李黔, 程桥, 等. 气体钻井全井段环空流场改善方法[J].
天然气工业, 2010, 30 (7) : 52 –54.
Liu Wei, Li Qian, Cheng Qiao, et al. Methods of improving the whole annulus flow field during gas drilling[J]. Natural Gas Industry, 2010, 30 (7) : 52 –54. |
| [13] | 韩占忠. Fluent流体工程仿真计算实例与应用[M]. 北京: 北京理工大学出版社, 2004 . |
| [14] |
熊莉芳, 林源, 李世武. k-ε湍流模型及其在FLUENT软件中的应用[J].
工业加热, 2007, 36 (4) : 13 –15.
Xiong Lifang, Lin Yuan, Li Shiwu. k-ε turbulent model and its application to the FLUENT[J]. Industrial Heating, 2007, 36 (4) : 13 –15. |
| [15] |
朱红钧, 林元华, 李强, 等. 空气钻井钻杆接头处流场及失效分析[J].
机械科学与技术, 2010, 29 (11) : 1534 –1536.
Zhu Hongjun, Lin Yuanhua, Li Qiang, et al. Flow properties and invalidation analysis of drill pipe joint by air drilling[J]. Mechanical Science and Technology for Aerospace Engineering, 2010, 29 (11) : 1534 –1536. |
| [16] |
严仁田, 王峰, 张德平, 等. 流场诱导API圆螺纹油管接箍失效分析及结构优化[J].
石油钻探技术, 2012, 40 (5) : 111 –114.
Yan Rentian, Wang Feng, Zhang Deping, et al. Failure analysis of API tubing round threaded connection induced by flow field[J]. Petroleum Drilling Techniques, 2012, 40 (5) : 111 –114. |
| [17] |
邓志安, 金磊, 陆忠义, 等. 天然气管线排液阀内流场压力特性数值模拟研究[J].
西安石油大学学报:自然科学版, 2013, 28 (3) : 70 –73.
Deng Zhi'an, Jin Lei, Lu Zhongyi, et al. Numerical simulation study on flow field pressure characteristics inside the drainage valve of the natural gas pipeline[J]. Journal of Xi'an Shiyou University:Natural Science Edition, 2013, 28 (3) : 70 –73. |
| [18] | 赵金洲, 张桂林. 钻井工程技术手册[M]. 北京: 中国石化出版社, 2004 : 321 -322. |
 2014, Vol. 36
2014, Vol. 36

