随着钻井技术向深井、超深井以及深海油气田开采的发展,钻柱的可靠性也受到了越来越严峻的挑战。在钻进和起下钻过程中,井口处钻柱的受力很复杂。起下钻时井口处钻柱受到最大拉力,如果猛提、猛刹,会使井口处钻柱受到的轴向拉力大大增加;钻进时,井口处钻柱所受的拉力和扭矩都很大[1-2],成为钻柱发生断裂事故的危险位置。
对于油气田钻井作业中的钻具断裂问题,从现场大多数钻具的断口分析可以判断为裂纹的动态扩展所致[3]。文献[4-5]的研究表明,具有任何形状的初始表面缺陷在经过几个疲劳裂纹扩展的循环后,都会发展成半椭圆裂纹的形状,因此将钻柱外表面的横向裂纹取为半椭圆形能较好地反映实际问题。由于裂纹形状的复杂性,对于实心或空心圆柱表面裂纹的研究主要是通过数值方法进行研究,且多为线弹性计算[6-14]。其中,文献[8]检验了二维和三维裂纹模型的位移外推法和J积分方法,对于是否在裂尖附近采用奇异元以及是否采用正交网格得到的J积分结果进行了对比研究,说明J积分不需要在裂尖周围采用奇异网格,也不要求划分正交网格,只需要保证回路积分的守恒性,很适合于研究具有复杂结构的裂纹体。关于圆柱体表面半椭圆裂纹的弹塑性断裂性能研究的文献很少,且多为单向荷载作用的情况。文献[15]利用J积分计算了弯矩作用下圆管的弹塑性断裂性能,通过和参考应力法的结果进行对照,说明了参考应力法的应用局限。文献[16]计算了拉力作用下圆柱的低周疲劳特性,表明塑性情况下,J积分强烈依赖于圆柱和裂纹的几何参数以及材料Ramberg-Osgood(R-O)本构模型中的硬化指数。
钻杆在正常情况下,都是在弹性范围内工作。但是当裂纹出现时,特别是相对裂纹深度较大、剩余连接韧带较薄的情况下,或者是非常恶劣的受力条件下,裂纹体的非弹性变形对断裂性能的影响就不再是小量。本文采用J积分数值研究钻柱外表面横向半椭圆裂纹在拉力和扭矩组合作用下的弹塑性断裂特性,研究钻井工况载荷条件下裂纹扩展至不同深度时裂纹面的形状,评价拉力波动和扭矩波动对井口附近钻柱断裂性能的影响。
1 力学模型井口附近的钻杆主要受到轴向拉力T和扭矩M作用,其裂纹面与钻柱轴线相垂直的情况最为危险[17]。以某超深直井用5~in.(1~in.=25.4 mm)钻杆为例,研究其本体外表面横向半椭圆裂纹在钻井载荷作用下的断裂特性。钻柱的外径D=127.0 mm,内径d=108.6 mm,壁厚t=9.19 mm。钻杆及其裂纹的受力和尺寸如图 1所示,其中裂纹的几何形状可由无因次的形状比a/c和相对裂纹深度a/t表示(a-半椭圆裂纹的深度,m;c-半椭圆裂纹的半宽度,m)。
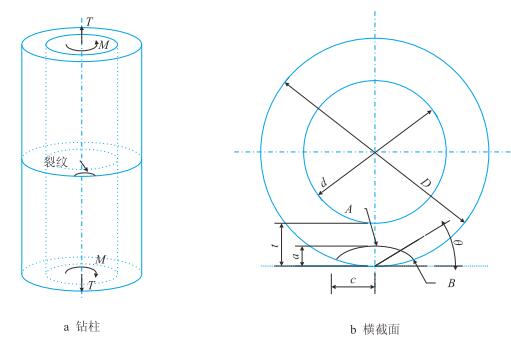 |
| 图1 拉力和扭矩组合作用下,钻柱及其含裂纹横截面示意图 Fig. 1 Sketch of forced drill string and arbitrary crack shape |
以30CrMo作为钻柱材料,通过拉伸试验测出其名义应力-应变曲线,再转换成真应力-真应变曲线[18],以R-O本构模型对实验数据进行拟合
| $ \frac{\varepsilon }{{{\varepsilon _{\rm{s}}}}} = \frac{\sigma }{{{\sigma _{\rm{s}}}}} + \alpha {\left( {\frac{\sigma }{{{\sigma _{\rm{s}}}}}} \right)^n} $ | (1) |
式中:
$\varepsilon$-应变,无因次;
$\varepsilon_{\rm s}$-屈服应变,无因次;
σ-应力,MPa;
$\sigma_{\rm s}$-屈服应力,MPa;
$\alpha$,n-材料本构常数,无因次。
30CrMo的材料常数:
弹性模量E=225.3 GPa;
泊松比$\mu$=0.28;
屈服应力$\sigma_{\rm s}$=700.1 MPa;
屈服应变$\varepsilon_{\rm s}$=0.003 1。
材料本构常数:
α=3.024;
n=12.89。
材料本构曲线如图 2所示。
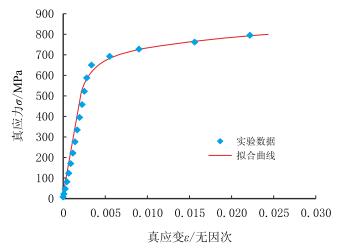 |
| 图2 30CrMo材料拉伸实验得到的真应力–真应变及其拟合的R–O本构曲线 Fig. 2 True stress-strain relationship and fitted R–O constitutional model of 30CrMo |
由于问题非对称,数值计算中需要模拟整个圆柱,将裂纹置于钻柱模型的中部,其网格划分如图 3所示。
 |
| 图3 有限元网格模型与裂纹面截面的局部网格划分 Fig. 3 The finite element model and enlarged drawing of crack section |
计算模型的长度取为2×150 mm[5],下端面约束其全部自由度;上端面自由,并施加拉力和扭矩。利用ABAQUS对裂纹体进行弹塑性分析,在裂纹前缘线的垂直面内取6个积分回路,以中间的4个回路积分的平均值作为该裂纹点的J积分[19],描述裂纹体拉伸和扭转组合载荷作用下的弹塑性断裂性能。
由于缺少可借鉴的中空圆柱外表面横向半椭圆裂纹的弹塑性J积分结果,本文关于J积分的数值计算有效性是通过与前人得到的弹性计算结果进行对比验证的,同时验证回路积分的路径无关性。以文献[20]中提到的Newman J C和Wang Q Z关于该裂纹体分别在拉力和扭矩单独作用下裂纹最深点A的K因子结果为参照。拉力单独作用下,A点的J积分按照式(2)转换成K因子
| $ K = \sqrt {\bar E \cdot J} $ | (2) |
平面应变条件下
平面应力条件下
式中:
K-应力强度因子,N/m$^{3/2}$;
E-杨氏弹性模量,Pa;
J-J积分,kN/m;
$\mu$-泊松比,无因次。
进一步利用式(3)进行无因次化
| $ F = \frac{K}{{\sigma \sqrt {{\rm{\pi }}a} }} $ | (3) |
式中:
F-无因次K因子;
σ-裂纹处的名义拉应力,MPa。
扭矩单独作用时,将式(2)中的E替换成2G(G-剪切弹性模量,Pa),将式(3)中的σ替换为裂纹处的名义剪应力τ。取裂纹形状比a/c=0.8,对于裂纹相对深度分别为0.2,0.4,0.6及0.8等4种情况进行线弹性计算。
对于裂纹最深点A,拉力单独作用下的有限元计算值与Newman J C所得结果之间的最大相对误差仅为0.70%,如图 4a所示;扭矩单独作用下的计算值与Wang Q Z所得结果的最大相对误差为2.60%,如图 4b所示;在所进行的8组计算中,沿所取的4个积分回路得到的J积分的最大相对误差只有0.12%,数值结果很好地保证了J积分的守恒性,由此说明,本文数值计算模型的可靠性,并将其直接推广应用到该裂纹体的弹塑性计算。
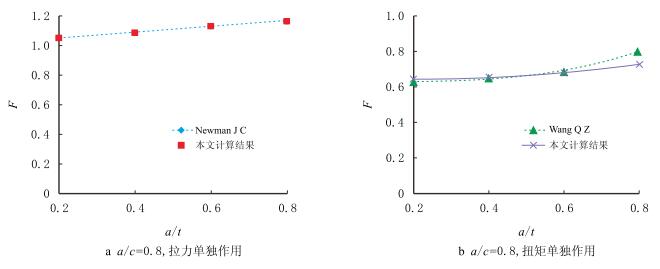 |
| 图4 有限元结果验证 Fig. 4 Finite element model validation |
对于某超深井的井口附近钻杆,考虑拉力T为1 050 kN、扭矩M为30 kN·m同时作用的钻井作业载荷,钻杆外表面横向半椭圆裂纹的相对深度a/t在0.1~0.9变化,裂纹形状比a/c在0.5~0.9变化。
基于方程(1)拟合得到的弹塑性本构关系,对含裂纹的钻杆进行弹塑性断裂力学分析。鉴于无因次分析的优点,将J积分按式(4)进行无因次化处理
| $ {J_0} = \frac{{J\bar E}}{{{\rm{\pi }}a{\sigma ^2}}} $ | (4) |
式中:J/0-无因次J积分。
3.1 裂纹的形状比在交变应力作用下,钻柱外表面的初始缺陷通常会扩展成为半椭圆裂纹。根据Paries公式,在加载方式、环境等外部条件相同的情况下,裂纹的扩展速率只与应力强度因子的变化幅值有关,在弹塑性情况下,则由J积分的变化幅值表示[16]。半椭圆裂纹前缘各点的扩展速率随相对位置θ、相对裂纹深度a/t和裂纹形状比a/c的不同而变化。对于同一相对裂纹深度的不同裂纹,存在一个临界形状比(a/c)cr,此时裂纹前缘最深点A和边界相邻点B处的J积分相等,该临界形状比确定的半椭圆可近似作为裂纹扩展至此深度时的裂纹面形状,不同裂纹相对深度条件下临界形状比的确定对于裂纹疲劳扩展的研究有重要的意义。
对于钻井载荷(T=1 050 kN,M=30 kN·m)作用下的井口附近钻杆,计算了相对裂纹深度a/t分别为0.2,0.4,0.6及0.8时,裂纹前缘最深点A和边界相邻点B的无因次J积分随形状比a/c的变化(如图 5所示,图中,实线对应裂纹最深点A,虚线对应边界相邻点B),两条线的交点对应的a/c即为临界形状比(如表 1所示)。可以看到,随着裂纹相对深度的增加,临界形状比是逐渐减小的,裂纹前缘会越来越平坦。
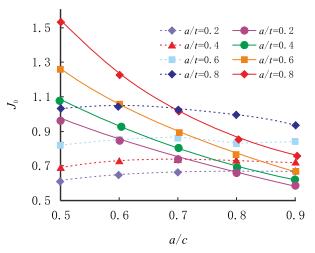 |
| 图5 无因次的J0随裂纹形状比的变化 Fig. 5 The variation of J0 along with crack aspect ratios |
| 表1 不同裂纹相对深度对应的临界形状比 Table 1 The transition aspect ratio varying with the relative crack depth |
钻杆在正常工作状态下是处于弹性范围内的,但是当初始裂纹发生较大范围的扩展时,材料的弹塑性影响可能就不再是小量了。假设裂纹在扩展过程中,其裂纹尖端的曲线近似为具有临界形状比的半椭圆,研究拉力和扭矩组合作用下,钻柱表面裂纹的弹塑性断裂性能随裂纹深度的变化,评价塑性变形对J积分的影响。
图 6给出裂纹相对深度a/t分别为0.2,0.5,0.7及0.9等4种情况下,裂纹尖端J积分在裂纹前缘分布的线弹性计算结果(图中虚线)和弹塑性计算结果(图中实线);表 2给出了不同相对裂纹深度条件下,裂纹前缘最深点A的塑性J积分Jp在整个J积分中所占的比例。
图 6和表 2中,除了a/t=0.9的结果对应于a/c=0.68以外,其他相对裂纹深度条件下的结果均对应于各自的临界形状比(见表 1)。可以看到,随着裂纹的扩展,裂纹前缘的J积分是单调增大的,且裂纹越深,其增大的速度越快;在裂纹相对深度较小时(比如a/t=0.2),裂尖附近的塑性区很小,可以近似为线弹性断裂;随着裂纹深度的增大,裂纹前缘附近的塑性区越来越大,其J积分沿裂纹前缘的分布曲线与线弹性计算结果的差异也越来越大,当a/t > 0.7以后塑性J积分Jp在整个J积分中所占的比例迅速增大,塑性变形对裂纹断裂性能的影响不再是小量;在裂纹相对深度达到0.9时,由于裂纹最深点附近的韧带很薄,发生了明显的塑性变形,使得J积分在裂纹最深点附近有显著的增大,Jp/J达到了23.9%。
| 表2 T=1 050 kN,M=30 kN·m条件下,JP/J随裂纹相对深度a/t变化 Table 2 The variations of JP/J along with a/t under T=1 050 kN, M=30 kN·m |
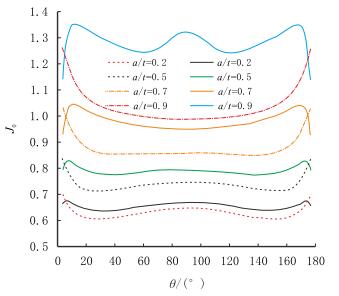 |
| 图6 T=1 050 kN,M=30 kN·m条件下,无因次J积分沿裂纹前沿的分布 Fig. 6 The variations of J0 along the crack front under T=1 050 kN, M=30 kN·m, in which real lines are elastic-plastic results and dashed lines are elastic results |
在需要进行上提钻杆解卡或使用震击器解卡操作中,上提力或震击力可能达到整个钻柱重量的数倍或接近最大钩载,而在钻头发生蹩钻或卡钻时,钻杆会承受瞬时超大扭矩的作用。对于井口附近的钻杆,以相对裂纹深度a/t=0.2、形状比a/c=0.79为例,研究拉力或扭矩变化对其断裂性能的影响,评价这两种主要载荷的波动对钻杆安全的损害。
为便于定量研究J积分关于拉力或扭矩的变化率,将J积分表示为
| $ J = \frac{{{J_{01}}{\rm{\pi }}a}}{{\bar E}}{\sigma ^2} + \frac{{{J_{02}}{\rm{\pi }}a}}{{\bar E}}{\tau ^2} $ | (5) |
式中:
$\tau$-剪应力,Pa;
J/01-对应于正应力σ的无因次J积分;
J/02-对应于剪应力$\tau$的无因次J积分。
用轴向拉力T和扭矩M可以将式(5)表示为
| $ J = \frac{{{J_{01}}{\rm{\pi }}a}}{{\bar E{S^2}}}{T^2} + \frac{{{J_{02}}{\rm{\pi }}a}}{{\bar E{{(2{I_{\rm{P}}}/D)}^2}}}{M^2} $ | (6) |
式中:
S-钻柱的横截面积,m2;
T-轴向拉力,kN;
$I_{\rm P}$-极惯性矩,m4;
D-钻柱外径,m;
M-扭矩,kN·m。
这样在得到无因次的J/01和J/02沿裂纹前缘的分布曲线后(J/01和J/02可以通过数值计算两组拉扭组合作用下的J积分后由式(6)换算得到),就可以方便地得到该裂纹在任意拉力和扭矩作用下裂纹前缘的J积分,同时由于式(6)将J积分表示成了关于T和M的显式形式,可以直接得到J积分关于T和M的变化率。
式(5)和式(6)的实质是将拉扭组合作用下的J积分等价为拉力和扭矩分别单独作用下的J积分之和,即利用了叠加原理。对于拉扭组合作用下含半椭圆表面裂纹的圆柱体,文献[11]在弹性范围内研究发现,当扭矩引起的剪应力小于拉力引起的正应力时,扭矩导致的裂纹面翘曲对叠加原理的影响非常微小,此时组合载荷作用下的K因子与各种载荷单独作用下的K因子之和近似相等,叠加原理成立。对于本文所研究的井口附近钻杆,考虑其拉力围绕T=1 050 kN上下波动30%,扭矩围绕M=30 kN·m上下波动30%,其最大扭矩对钻杆产生的剪应力仍小于最小拉力产生的正应力,在弹性范围内符合叠加原理适用的条件。
为验证叠加原理在井口附近钻杆弹塑性断裂研究中的适用性,任取两组载荷:(1) T=1 050 kN和M=20 kN·m;(2) T=1 050 kN和M=40 kN·m。通过有限元计算得到其各自的J积分后,由式(6)反算得到J/01与J/02沿裂纹前缘的分布如图 7所示。
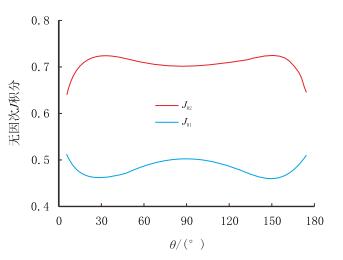 |
| 图7 无因次的J01和J02沿裂纹前缘的分布 Fig. 7 The variations of J01 and J02 along the crack front |
首先固定扭矩M=30 kN·m,拉力T围绕1 050 kN上下波动30%,分别通过叠加原理式(6)和
有限元计算得到的A点J积分随拉力的变化如图 8所示,两者最大相对误差为9.1%。然后固定拉力T=1 050 kN,扭矩M围绕30 kN·m上下波动30%,通过叠加原理和有限元计算得到A点J积分随扭矩的变化如图 9所示,两者最大相对误差仅为2.1%。由此说明对于拉扭组合作用下的井口附近钻杆,叠加原理也是近似成立的。
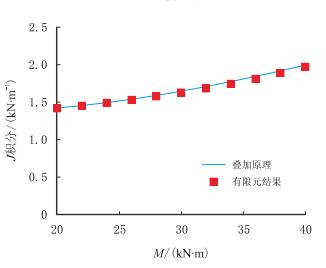 |
| 图9 T=1 050 kN时A点的J积分随扭矩M的变化 Fig. 9 J-integral of point A varying along torque M under T=1 050 kN |
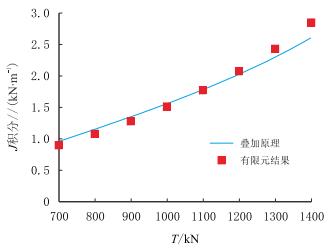 |
| 图8 M=30 kN·m时A点的J积分随拉力T的变化 Fig. 8 J-integral of point A varying along tension force T under M=30 kN·m |
J积分对拉力变化和对扭矩变化的敏感度可以通过对式(6)求偏导得到
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial J}}{{\partial T}} = \frac{{2{J_{01}}{\rm{\pi }}a}}{{\bar E{S^2}}}T{\rm{ }}}\\ {\frac{{\partial J}}{{\partial M}} = \frac{{2{J_{02}}{\rm{\pi }}a}}{{\bar E{{(2{I_{\rm{P}}}/D)}^2}}}M} \end{array}} \right. $ | (7) |
在本文所研究的拉力T=1 050 kN、扭矩M=30 kN·m的条件下,裂纹最深点A的J积分随拉力的变化率为2.14)×10-3 m-1,随扭矩的变化率为2.83)×10-2 m-2。保持扭矩M=30 kN·m不变,当轴向拉力围绕1 050 kN上下波动30%时,
将钻柱外表面的缺陷简化为横向半椭圆裂纹,以30CrMo作为钻柱材料并通过实验拟合得到R-O本构模型,以某超深直井井口附近钻杆的实际工况载荷为例,数值研究了井口附近钻杆的弹塑性断裂性能,得到以下结论:
(1)半椭圆表面裂纹的临界形状比随裂纹相对深度的增大而减小,当裂纹相对深度由0.1增大到0.8,其临界形状比由0.80降低到0.68,即随着裂纹扩展,其裂纹前缘越来越平坦。
(2)随着裂纹的扩展,裂纹前缘附近的塑性区越来越大,当相对裂纹深度a/t > 0.7以后,J积分中的塑性成分$J_{\rm P}$在整个J积分中所占的比例迅速增大,采用计入钻柱弹塑性断裂特性的J积分才能更好地描述钻柱疲劳裂纹扩展的全寿命。
(3)对于井口附近钻杆所受到的拉扭组合载荷,验证了叠加原理对其外表面半椭圆裂纹断裂性能的适用性,通过研究J积分分别相对于拉力和扭矩的变化率发现,扭矩波动对J积分的影响远大于拉力波动对J积分的影响,钻柱表面裂纹在扭矩波动下更容易扩展,对钻柱的危害也更大。预防钻井过程中的蹩钻和卡钻现象,避免钻柱受到扭转冲击对延长钻柱寿命有重要意义。
| [1] |
林铁军, 练章华, 张俊良, 等. 气体钻与泥浆钻全井段钻柱动力学对比研究[J].
西南石油大学学报:自然科学版, 2011, 33 (1) : 139 –143.
Lin Tiejun, Lian Zhanghua, Zhang Junliang, et al. Comparative study on dynamics behaviors of the full drillstring between gas drilling and mud drilling[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2011, 33 (1) : 139 –143. |
| [2] |
林铁军, 练章华, 曾晓健, 等. 应用XFEM模拟研究钻杆裂纹扩展过程[J].
重庆大学学报, 2010, 33 (7) : 123 –128.
Lin Tiejun, Lian Zhanghua, Zeng Xiaojian, et al. Simulation on crack growth of drill pipe with XFEM[J]. Journal of Chongqing University, 2010, 33 (7) : 123 –128. |
| [3] | 董洪生.川东北地区钻具故障现状分析[R].上海:川东北工区钻具应用研讨会, 2007. |
| [4] | Lin X B, Smith R A. Shape growth simulation of surface cracks in tension fatigued round bars[J]. International Journal of Fatigue, 1997, 19 (6) : 461 –469. DOI:10.1016/S0142-1123(97)00012-1 |
| [5] | Carpinteri A. Shape change of surface cracks in round bars under cyclic axial loading[J]. International Journal of Fatigue, 1993, 15 (1) : 21 –26. DOI:10.1016/0142-1123(93)90072-X |
| [6] | Manuel da Fonte, Manuel de Freitas. Stress intensity factors for semi-elliptical surface cracks in round bars under bending and torsion[J]. International Journal of Fatigue, 1999, 21 : 457 –463. DOI:10.1016/S0142-1123(98)00090-5 |
| [7] | Toribio J, Álvarez N, González B, et al. A critical review of stress intensity factor solutions for surface cracks in round bars subjected to tension loading[J]. Engineering Failure Analysis, 2009, 16 : 794 –809. DOI:10.1016/j.engfailanal.2008.06.023 |
| [8] | Courtin S, Gardin C, Bezine G, et al. Advantages of the J-integral approach for calculating stress intensity factors when using the commercial finite element software ABAQUS[J]. Engineering Fracture Mechanics, 2005, 72 : 2174 –2185. DOI:10.1016/j.engfracmech.2005.02.003 |
| [9] | Toribio J, Matos J C, Gonzalez B, et al. Numerical modelling of crack shape evolution for surface flaws in round bars under tensile loading[J]. Engineering Failure Analysis, 2009, 16 : 618 –630. DOI:10.1016/j.engfailanal.2008.02.014 |
| [10] | Carpinteri A, Brighenti R. Part-through cracks in round bars under cyclic combined axial and bending loading[J]. International Journal of Fatigue, 1996, 18 (1) : 33 –39. DOI:10.1016/0142-1123(95)00076-3 |
| [11] | Ismail A E, Ariffin A K, Abdullah S, et al. Stress intensity factors for surface cracks in round bar under single and combined loadings[J]. Meccanica, 2012, 47 : 1141 –1156. DOI:10.1007/s11012-011-9500-7 |
| [12] | Shahani A R, Habibi S E. Stress intensity factors in a hollow cylinder containing a circumferential semi-elliptical crack subjected to combined loading[J]. International Journal of Fatigue, 2007, 29 : 128 –140. DOI:10.1016/j.ijfatigue.2006.01.017 |
| [13] | Kou K P, Burdekin F M. Stress intensity factors for a wide range of long-deep semi-elliptical surface cracks, partly through-wall cracks and fully through-wall cracks in tubular members[J]. Engineering Fracture Mechanics, 2006, 73 : 1693 –1710. DOI:10.1016/j.engfracmech.2006.02.010 |
| [14] | Predan J, Mocilnik V, Gubeljak N. Stress intensity factors for circumferential semi-elliptical surface cracks in a hollow cylinder subjected to pure torsion[J]. Engineering Fracture Mechanics, 2013, 105 : 152 –168. DOI:10.1016/j.engfracmech.2013.03.033 |
| [15] | Mechab B, Serier B, Bouiadjra B B, et al. Linear and nonlinear analyses for semi-elliptical surface cracks in pipes under bending[J]. International Journal of Pressure Vessels and Piping, 2011, 88 : 57 –63. DOI:10.1016/j.ijpvp.2010.11.001 |
| [16] | Findley K O, Koh S W, Saxena A. J-integral expressions for semi-elliptical cracks in round bars[J]. International Journal of Fatigue, 2007, 29 : 822 –828. DOI:10.1016/j.ijfatigue.2006.09.001 |
| [17] | 张俊清.高速列车空心车轴表面裂纹应力强度因子研究[D].北京:北京交通大学, 2011. http://cdmd.cnki.com.cn/article/cdmd-10004-1011102786.htm |
| [18] |
邹吉权, 荆洪阳, 霍立兴, 等. 31Si2MnCrMoVE钢薄板试样表面裂纹断裂韧度测试[J].
机械工程学报, 2007, 43 (8) : 212 –217.
Zou Jiquan, Jing Hongyang, Huo Lixing, et al. Surfacecrack fracture toughness test of 31Si2MnCrMoVE steel on thin plate[J]. Chinese Journal of Mechanical Engineering, 2007, 43 (8) : 212 –217. DOI:10.3901/JME.2007.08.212 |
| [19] | Kim Y J, Kim J S, Park Y J, et al. Elastic-plastic fracture mechanics method for finite internal axial surface cracks in cylinders[J]. Engineering Fracture Mechanics, 2004, 71 : 925 –944. DOI:10.1016/S0013-7944(03)00159-0 |
| [20] | 中国航空研究院. 应力强度因子手册[M]. 北京: 科学出版社, 1993 . |
 2014, Vol. 36
2014, Vol. 36

